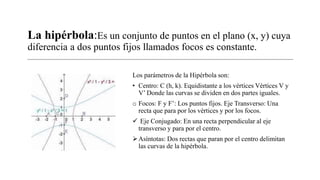
Este documento resume los conceptos fundamentales del pensamiento geométrico y analítico. Define las rectas, circunferencias, elipses, parábolas e hipérbolas, incluyendo sus parámetros y ecuaciones. También explica la ecuación general de segundo grado y proporciona referencias bibliográficas.

1. Pensamiento
Geométrico y
Analítico.

2. Por
Paula Andrea Naranjo Rodríguez
1003706466
Algebra, Trigonometría y Geometría analítica– 551108
Grupo 31
Presentado a
Stevenson Lions.
Universidad Nacional Abierta y a Distancia UNAD.
CEAD de Girardot
Ciencias de la educación ECEDU
28-11-21

3. Introducción.
En el siguiente trabajo se tiene
como objetivo conocer mas
acerca del pensamiento
geométrico y analítico por
medio de su definición y unos
ejercicios que nos ayudaran a
comprender cada temática,
finalizando con sus debidas
referencias bibliográficas.

4. Análisis de la recta:Una recta es una
sucesión de puntos colineales; es decir, puntos
ubicados uno tras otro de tal manera que uno
esconde al anterior cuando se observa la fila de
frente.
Los parámetros de la recta son:
• La Pendiente Se simboliza con la letra m, esta
relacionado con la inclinación que tiene la recta
respecto al eje x.
• El Intercepto Se simboliza con la letra b, esta
relacionado con el punto donde la recta corta al eje
y.
La ecuación de la recta:
 Ecuación Canónica Llamada también ecuación
analítica, ya que por medio de ésta se puede inferir
el comportamiento de la recta.
 Ecuación General Es una ecuación de primer
grado.

5. La circunferencia:Es un conjunto de puntos
(x, y) en el plano cartesiano que equidistan a un punto fijo
llamado centro. La distancia fija se le llama radio.
Los parámetros de la circunferencia son:
• Centro: La coordenada en x se le denomina h y
la de y se le denomina k. C(h, k)
Radio: Es la distancia del centro a cualquier
punto de la misma, se representa por R.
ELIPSE: Es un conjunto de puntos (x, y) en el
plano cartesiano, tal que la suma de sus distancias
a dos puntos fijos llamados focos, es constante.

6. La parábola: Es un conjunto de puntos en el plano (x, y) que se
encuentran a la misma distancia de un punto fijo F llamado foco y una
recta D llamada directriz.
Los parámetros de la parábola son:
• Vértice V (h, k): Donde la curva se divide en dos partes iguales.
 Foco: F: El punto fijo a una distancia p del vértice, llamada
distancia focal.
 Eje de Simetría: Una recta que para por el vértice y es
perpendicular a la directriz.
 Directriz D: Recta ubicada a la misma distancia que el foco pero
en sentido contrario.
Ecuación Canónica: (Eje de Simetría vertical) Toda parábola con
eje de simetría vertical y vértice en el origen.
Ecuación Canónica: (Eje de Simetría horizontal) Toda parábola con
eje de simetría horizontal y vértice en el origen.

7. La hipérbola:Es un conjunto de puntos en el plano (x, y) cuya
diferencia a dos puntos fijos llamados focos es constante.
Los parámetros de la Hipérbola son:
• Centro: C (h, k). Equidistante a los vértices Vértices V y
V’ Donde las curvas se dividen en dos partes iguales.
o Focos: F y F’: Los puntos fijos. Eje Transverso: Una
recta que para por los vértices y por los focos.
 Eje Conjugado: En una recta perpendicular al eje
transverso y para por el centro.
Asíntotas: Dos rectas que paran por el centro delimitan
las curvas de la hipérbola.

8. Ecuación general de segundo grado:
Una ecuación de segundo grado o ecuación cuadrática de una variable
es una ecuación que tiene la expresión general donde X es la variable; y
a, b y c constantes, a es el cociente cuadrático, b es el cociente lineal y c
es el termino independiente.

9. Referencias bibliográficas:
Ecuación de segundo grado - Wikipedia, la enciclopedia libre.
Rondón, J. (2017). Algebra, Trigonometría y Geometría Analítica. Bogotá
D.C.: Universidad Nacional Abierta y a Distancia. Páginas 237 – 265.
Recuperado de https://repository.unad.edu.co/handle/10596/11583
Ortiz Ceredo, F. J. Ortiz Ceredo, F. J. y Ortiz Ceredo, F. J. (2018).
Matemáticas 3 (2a. ed.). Grupo Editorial Patria. https://elibro-
net.bibliotecavirtual.unad.edu.co/es/ereader/unad/40539?page=51
Real, M. (2010). Secciones Cónicas. Recuperado
de https://repository.unad.edu.co/handle/10596/7690