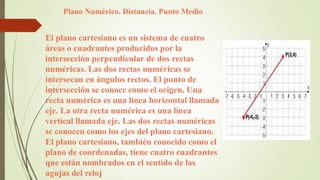
El documento describe los conceptos básicos del plano cartesiano, incluyendo sus cuatro cuadrantes y ejes. También define la distancia entre puntos y la noción de punto medio. Finalmente, introduce las ecuaciones y representaciones gráficas de circunferencias, parábolas, elipses e hipérbolas.

1. República Bolivariana De Venezuela
Universidad Politécnica Territorial Andrés Eloy Blanco
Barquisimeto- Estado Lara
Plano Numérico
Nombre: Jhonder Abreu David Mejías
Cedula:30529335
Sección: 0103

2. Plano Numérico. Distancia. Punto Medio
El plano cartesiano es un sistema de cuatro
áreas o cuadrantes producidos por la
intersección perpendicular de dos rectas
numéricas. Las dos rectas numéricas se
intersecan en ángulos rectos. El punto de
intersección se conoce como el origen. Una
recta numérica es una línea horizontal llamada
eje. La otra recta numérica es una línea
vertical llamada eje. Las dos rectas numéricas
se conocen como los ejes del plano cartesiano.
El plano cartesiano, también conocido como el
plano de coordenadas, tiene cuatro cuadrantes
que están nombrados en el sentido de las
agujas del reloj

3. Distancia
Cuando algún punto se encuentra en el eje de
las x o de las abscisas o en una recta paralela a
éste eje, la distancia entre los puntos
corresponde al valor absoluto de las diferencia
de sus abscisas. ... (x 2 – x 1 ) •La distancia de
un punto, P, a un plano, π, es la menor de la
distancia desde el punto a los infinitos puntos
del plano. •Esta distancia corresponde a la
perpendicular trazada desde el punto al plano.

4. Punto medio
Es el punto que se encuentra a la
misma distancia de otros dos puntos
cualquiera o extremos de un segmento.
Más generalmente punto equidistante
en matemática, es el punto que se
encuentra a la misma distancia de dos
elementos geométricos, ya sean puntos,
segmentos, rectas, etc.

5. Ecuaciones y trazado de
circunferencias
Está dada por: Ax + By + Cz + D = 0, es decir, los puntos del espacio ( x,
y, z) que satisfacen la ecuación y forman un plano. ... Se escribe como
un sistema de ecuaciones correspondiente. Se eliminan los parámetros
para encontrar una única ecuación lineal en variables x, y, z. La
circunferencia es el lugar geométrico de los puntos del plano que
equidistan de un punto fijo llamado centro (recordar que estamos
hablando del Plano Cartesiano y es respecto a éste que trabajamos).
Determinación de una circunferencia Una circunferencia queda
determinada cuando conocemos:
a) Tres puntos de la misma, equidistantes del centro.
b) El centro y el radio.
c) El centro y un punto en ella.
d) El centro y una recta tangente a la circunferencia

6. Parábolas
Una parábola es la sección cónica de
excentricidad igual a 1, ​ resultante de
cortar un cono recto con un plano
cuyo ángulo de inclinación respecto
al eje de revolución del cono sea igual
al presentado por su generatriz. El
plano resultará por lo tanto paralelo
a dicha recta.​​​

7. Elipse
Una elipse es una curva plana, simple​
y cerrada con dos ejes de simetría que
resulta al cortar la superficie de un
cono por un plano oblicuo al eje de
simetría con ángulo mayor que el de la
generatriz respecto del eje de
revolución

8. Hipérbola
Es una curva abierta de dos
ramas, obtenida cortando un
cono recto mediante un plano
no necesariamente paralelo al
eje de simetría, y con ángulo
menor que el de la generatriz
respecto

9. Representar Graficamente Las Ecuaciones
De Las Conicas