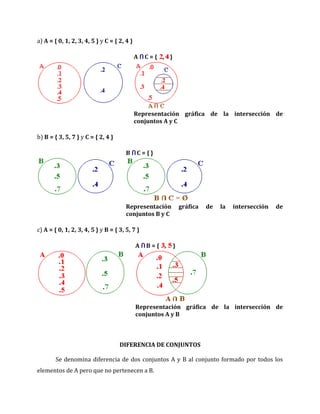
El documento describe los diagramas de Venn y sus usos para representar conjuntos y operaciones entre ellos. Explica las operaciones de unión, intersección, diferencia y complemento de conjuntos a través de definiciones matemáticas y ejemplos ilustrados con diagramas de Venn.

1. DIAGRAMA DE VENN
A cada conjunto se le considera encerrado dentro de una curva (plana) cerrada. Los
elementos del conjunto considerado pueden ser específicamente dibujados o pueden
quedar (implícitamente) sobreentendidos. Los diagramas son empleados, para representar
tanto a los conjuntos como a sus operaciones, y constituyen una poderosa herramienta
geométrica, desprovista de validez lógica. A continuación representaremos algunos
conjuntos y verificaremos algunas igualdades (las intersecciones de dos o más conjuntos
quedan caracterizados por el rayado múltiple).
El gráfico es la representación de la unión
El gráfico es la representación de la intersección
El gráfico es la representación de la diferencia
UNIÓN DE CONJUNTOS
La unión de los conjuntos A y B es el conjunto formado por todos los elementos que
pertenecen a A o a B o a ambos. Se denota: A U B. La unión de conjuntos se define como:
A U B = {x / x Aox B}
En forma gráfica:

2. Cuando no tienen Cuando tienen algunos Cuando todos los elementos de un
elementos comunes elementos comunes conjunto pertenecen a otro conjunto
Ejemplos:
1. Dados los conjuntos: A = {0, 1, 2, 3, 4, 5}, B = { 0, 2, 4 } y C = { 5, 6, 8 }, efectuar y construir
los diagramas respectivos:
a) A U C b) B U C c) A U B
Tenemos:
a) A = { 0, 1, 2, 3, 4, 5 } y C = { 5, 6, 8 }
A U C = { 0, 1, 2, 3, 4, , 6, 8 }
Representación gráfica de la unión de conjuntos A y
C
b) B = {0, 2, 4 } y C = { 5, 6, 8 }
B U C = { 0, 2, 4, 5, 6, 8 }
Representación gráfica de la unión de conjuntos B y C

3. c) A = { 0, 1, 2, 3, 4, 5 } y B = { 0, 2, 4 }
A U B = { , 1, , 3, , 5 }
Representación gráfica de la unión de conjuntos A y B
INTERSECCIÓN DE CONJUNTO
Se define la intersección de dos conjuntos A y B al conjunto de elementos que son
comunes a A y B. Se denota por A B, que se lee: A intersección B. La intersección de A y B
también se puede definir:
A B={x/x Ayx B } y mediante un diagrama de Venn-Euler:
Cuando tienen Cuando no tienen Cuando todos los elementos de un
elementos comunes elementos comunes conjunto pertenecen a otro conjunto
Ejemplos:
1. Dados los conjuntos: A = { 0, 1, 2, 3, 4, 5 }, B = { 3, 5, 7 } y C = { 2, 4 }, efectuar y construir
los diagramas respectivos:
a) A C b) B C c) A B

4. a) A = { 0, 1, 2, 3, 4, 5 } y C = { 2, 4 }
A C={ , }
Representación gráfica de la intersección de
conjuntos A y C
b) B = { 3, 5, 7 } y C = { 2, 4 }
B C={}
Representación gráfica de la intersección de
conjuntos B y C
c) A = { 0, 1, 2, 3, 4, 5 } y B = { 3, 5, 7 }
A B={ , }
Representación gráfica de la intersección de
conjuntos A y B
DIFERENCIA DE CONJUNTOS
Se denomina diferencia de dos conjuntos A y B al conjunto formado por todos los
elementos de A pero que no pertenecen a B.

5. La diferencia se denota por: A - B que se lee: A diferencia B o A menos B. Se define la
diferencia de dos conjuntos también como:
A - B = {x / x Ayx B}
Mediante un diagrama de Venn - Euler:
Cuando no tienen Cuando tienen Cuando todos los elementos de un
elementos comunes elementos comunes conjunto pertenecen a otro conjunto
Ejemplos:
1. Dados los conjuntos: A = { a, b, c, d, e }, B = { a, e } y C = { d, f, g }, efectuar y construir los
diagramas respectivos:
a) A - C b) B - C c) A - B
a) A = { a, b, c, d, e } y C = { d, f, g }
A - C = { a, b, c, e }
Representación gráfica de la diferencia de conjuntos A y C
b) B = { a, e } y C = { d, f, g }
B - C = { a, e }

6. c) A = { a, b, c, d, e } y B = { a, e }
A - B = { b, c, d }
Representación gráfica de la diferencia de conjuntos A y B
COMPLEMENTO DE UN CONJUNTO
Si un conjunto A es subconjunto de otro conjunto universal U, al conjunto A' formado
por todos los elementos de U pero no de A, se llama complemento de A con respecto a U.
Simbólicamente se expresa:
A' = { x/x Uyx A}
Ejemplos:
a) Sean U = { m, a, r, t, e } y A = { t, e }
Su complemento de A es: A' = { m, a, r }
En forma gráfica:
b) Sean U = { letras de la palabra aritmética} y B = { vocales de la palabra vida }
Determinado por extensión tenemos
U = { a, r, i, t, m, e, c } B = { i, a }
Su complemento de B es: B' = { r, t, m, e, c }

7. En forma gráfica: