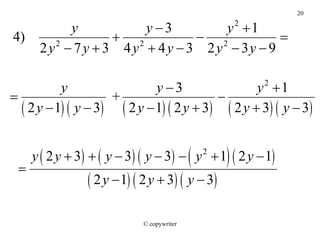Este documento presenta los conceptos y procedimientos para trabajar con expresiones racionales, incluyendo definirlas, simplificarlas, multiplicarlas, dividirlas, sumarlas y restarlas. También cubre cómo simplificar fracciones complejas dividiendo expresiones racionales.

1. Expresiones Racionales © copywriter

2. Definir el concepto de expresión racional . Simplificar expresiones racionales . Multiplicar expresiones racionales Dividir expresiones racionales Sumar expresiones racionales. Restar expresiones racionales . Simplificar fracciones complejas. Objetivos © copywriter

3. Definición Una expresión racional es una expresión de la forma , donde p(x) y q(x) son polinomios y © copywriter

4. Ejemplos de expresiones racionales © copywriter

5. Procedimiento para simplificar expresiones racionales Factorice completamente el numerador y el denominador de la expresión racional. Cancele o divida aquellos factores que sean comunes (iguales) en el numerador y en el denominador . Simplificación de expresiones racionales © copywriter

6. Ejemplos Simplifique cada expresión racional. © copywriter

7. © copywriter

8. Procedimiento para multiplicar expresiones racionales Factorizar los numeradores y denominadores de las expresiones racionales. Dividir los factores comunes que hayan entre los numeradores y denominadores. Multiplicar los numeradores y colocar el resultado sobre la multiplicación de los denominadores. Multiplicación de expresiones racionales © copywriter

9. Ejemplos © copywriter

10. © copywriter

11. Procedimiento para dividir expresiones racionales La división se cambia a la multiplicación por el reciproco del divisor. Factorizar los numeradores y denominadores de las expresiones racionales. Dividir los factores comunes que hayan entre los numeradores y denominadores. Multiplicar los numeradores y colocar el resultado sobre la multiplicación de los denominadores. División de expresiones racionales © copywriter

12. Ejemplos Lleva a cabo la operación indicada. © copywriter

13. © copywriter

14. © copywriter

15. Procedimiento para sumar y/o restar expresiones racionales. Para sumar o restar expresiones racionales con el mismo denominador; sumamos o restamos los numeradores conservando el denominador común. Para sumar o restar expresiones racionales con denominadores distintos, Encuentra un denominador común, el denominador común recomendado es el mínimo común múltiplo. Suma y resta de expresiones racionales © copywriter

16. Encuentra las expresiones equivalentes usando el denominador común. Suma o resta los numeradores y coloca el resultado sobre el denominador común. Simplifica si es posible. © copywriter

17. Efectúe la operación indicada. © copywriter

18. © copywriter

19. © copywriter

20. © copywriter

21. © copywriter

22. © copywriter

23. Ejemplos Definición Una fracción compleja es una división de dos expresiones racionales. © copywriter

24. Procedimiento para simplificar fracciones complejas. Simplifica las operaciones en el numerador. Simplifica las operaciones en el denominador. Cambia la división a la multiplicación por el reciproco del divisor. Multiplica las expresiones racionales. © copywriter

25. Encuentra el denominador común de los denominadores en las expresiones racionales del numerador y del denominador. Multiplica el numerador y el denominador de la fracción compleja por el denominador común. Procedimiento alterno para simplificar fracciones complejas © copywriter

26. Ejemplos: Simplifique cada fracción compleja. © copywriter

27. © copywriter

28. © copywriter

29. Simplifica la fracción compleja simplificando el numerador y el denominador primero. Ver otros ejemplos pág. 40. © copywriter