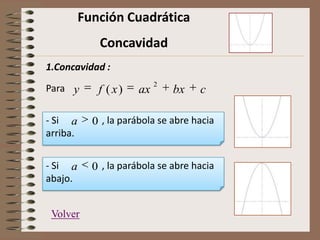
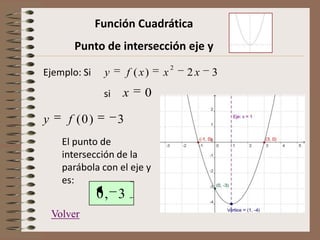
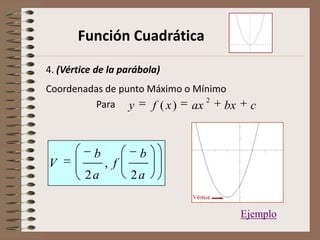
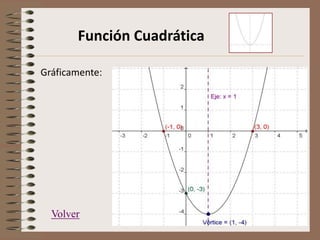
Este documento describe las características de las funciones cuadráticas. Explica cómo calcular la concavidad, los puntos de corte con el eje x, el punto de intersección con el eje y, las coordenadas del vértice, y el eje de simetría de una función cuadrática dada. También muestra cómo graficar funciones cuadráticas.

1. Función Cuadrática
Entrar

2. Función Cuadrática
Como ya vimos en
la actividad de
exploración ya
sabemos que con
los valores de los
coeficientes de la
función
cuadrática, podemo
s graficar la curva.
0
)(
2
a
cbxaxxfy
Donde , y
son los coeficientes de
la función
ba c
Siguiente

3. Función Cuadrática
Dominio de la función
2
)( xxfy
Siguiente
.Dom
Imagen de la función ,0Im
EJEMPLO

4. Función Cuadrática
Concavidad
Puntos de corte eje x. (discriminante)
Intersección de la parábola con el eje y
Coordenadas del vértice
Máximo y mínimo
Eje de simetría
Gráfica
Ejercicios
Aplicaciones Salir
Veremos sus características:

5. Función Cuadrática
Concavidad
- Si , la parábola se abre hacia
arriba.
0a
Para cbxaxxfy
2
)(
- Si , la parábola se abre hacia
abajo.
0a
1.Concavidad :
Volver

6. Función Cuadrática
2. Análisis de discriminante acbx 4
2
Si , debemos encontrar las soluciones de
la ecuación de segundo grado para determinar los
puntos de intersección de la parábola con el eje x
0x
Volver
Observación importante:

7. Función Cuadrática
2. Análisis de discriminante acbx 4
2
Si , la parábola corta en dos
puntos al eje x
0x
Si , la parábola corta en un
único punto al eje x
Si , la parábola no corta al
eje x
0x
0x
Siguiente

8. Ejemplo: Concavidad
Puntos de corte con el eje x-
Análisis del discriminante
Grafique 32)(
2
xxxfy
1. Concavidad: 01a
2. Análisis de discriminante:
3;2;1 cba
acbx 4
2
016x
Entonces la parábola corta en dos puntos al eje x
032
2
xx
1
3
2
1
x
x Puntos de intersección de la
parábola con el eje x (3,0) y
(-1,0)
La parábola se abre
hacia arriba.
Siguiente

9. Función Cuadrática
3. Punto de intersección de la parábola con el eje y
Para cbxaxxfy
2
)( , si 0x
cfy )0(
c,0
espuntoeltantolopor
EjemploVolver

10. Función Cuadrática
Punto de intersección eje y
Ejemplo: Si 32)(
2
xxxfy
si 0x
3)0(fy
El punto de
intersección de la
parábola con el eje y
es:
3,0
Volver

11. Función Cuadrática
4. (Vértice de la parábola)
Coordenadas de punto Máximo o Mínimo
Para cbxaxxfy
2
)(
a
b
f
a
b
V
2
,
2
Ejemplo

12. Función Cuadrática
Calculo del vértice
Ejemplo: Si 32)(
2
xxxfy
3;2;1 cba
Reemplazando:
12
)2(
,
12
)2(
fV 1,1 fV
5)1(
2)1(2)1()1(
2
f
f
Siguiente
a
b
f
a
b
V
2
,
2
Por tanto el vértice es
5,1V

13. Función Cuadrática
5. Máximo o Mínimo
- Si , la parábola se abre hacia
arriba.Tiene valor mínimo
0a
- Si , la parábola se abre hacia
abajo. Tiene valor máximo
0a
Volver

14. Función Cuadrática
Ejemplo: Máximo y mínimo
5. Máximo o mínimo: Si 01a
La parábola se abre hacia
arriba. Tiene valor mínimo.
Y se encuentra en el punto
del vértice (- 1, 5)
Siguiente
32)(
2
xxxfy

15. Función Cuadrática
6. Eje de simetría
Por el punto
EjemploVolver
a
b
f
a
b
2
,
2
La ecuación del eje simetría es
a
b
x
2

16. Función Cuadrática
Eje de simetría
6. Eje de simetría
Si , en la función 32)(
2
xxxfy
Siguiente
5,1V
entonces
1x

17. Función Cuadrática
Gráficamente:
Volver

18. Función Cuadrática
- Grafica las siguientes parábolas.
84)(.7
32)(.6
12)(.5
32)(.4
232)(.3
12)(.2
32)(.1
2
2
2
2
2
2
2
xxfy
xxfy
xxxfy
xxxfy
xxxfy
xxxfy
xxxfy
Volver

19. Función Cuadrática
Volver
9.Aplicaciones
Lanzamiento de un proyectil
Aplicaciones de la función