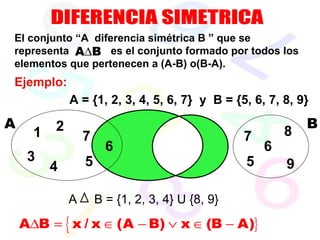
El documento explica diferentes operaciones entre conjuntos como unión, intersección, diferencia y diferencia simétrica. Proporciona ejemplos numéricos para ilustrar cada operación. También define el complemento de un conjunto y presenta ejemplos adicionales de cálculos entre conjuntos.

2. 7 6 5 5 6 UNION DE CONJUNTOS A B El conjunto “A unión B” que se representa asi es el conjunto formado por todos los elementos que pertenecen a A,a B o a ambos conjuntos. Ejemplo: 9 8 7 3 1 4 2 A = {1, 2, 3, 4, 5, 6, 7} y B = {5, 6, 7, 8, 9} A U B = {1, 2, 3, 4, 5, 6, 7, 8, 9}

3. 7 6 5 5 6 A B El conjunto “A intersección B” que se representa es el conjunto formado por todos los elementos que pertenecen a A y pertenecen a B. Ejemplo: 9 8 7 3 1 4 2 INTERSECCION DE CONJUNTOS A = {1, 2, 3, 4, 5, 6, 7} y B = {5, 6, 7, 8, 9} A B = { 5, 6, 7}

4. 7 6 5 5 6 A B El conjunto “A menos B” que se representa es el conjunto formado por todos los elementos que pertenecen a A y no pertenecen a B. Ejemplo: 9 8 7 3 1 4 2 DIFERENCIA DE CONJUNTOS A = {1, 2, 3, 4, 5, 6, 7} y B = {5, 6, 7, 8, 9} A – B = {1, 2, 3, 4}

5. 7 6 5 5 6 A B El conjunto “B menos A” que se representa es el conjunto formado por todos los elementos que pertenecen a B y no pertenecen a A. Ejemplo: 9 8 7 3 1 4 2 ¿A-B=B-A? A = {1, 2, 3, 4, 5, 6, 7} y B = {5, 6, 7, 8, 9} B – A = {8, 9}

6. 7 6 5 5 6 A B El conjunto “A diferencia simétrica B ” que se representa es el conjunto formado por todos los elementos que pertenecen a (A-B) o(B-A). Ejemplo: 9 8 7 3 1 4 2 DIFERENCIA SIMETRICA A = {1, 2, 3, 4, 5, 6, 7} y B = {5, 6, 7, 8, 9} A B = {1, 2, 3, 4} U {8, 9}

7. También es correcto afirmar que: A B A-B B-A A B

8. COMPLEMENTO DE UN CONJUNTO Dado un conjunto universal U y un conjunto A,se llama complemento de A al conjunto formado por todos los elementos del universo que no pertenecen al conjunto A. Notación: A’ o A C Ejemplo: U ={1,2,3,4,5,6,7,8,9} A ={1,3, 5, 7, 9} y Simbólicamente: A’ = U - A

9. 1 2 3 4 5 6 7 8 9 U A A A’={2,4,6,8}

11. Dados los conjuntos: A = { 4, 7, 10, ... ,34} B = { 2, 4, 6,...,26} C = { 7,11,15,...,31} a) Expresar B y C por extensión b) Calcular: A B , C – A 1

12. a) A = {4,7,10,13,16,19,22,25,28,31,34} B = {2,4,6,8,10,12,14,16,18,20,22,24,26} C = {7,11,15,19,23,27,31} A B = { 4,10,16,22 } C – A = { 11,15,23,27 } Sabemos que A B esta formado por los elementos comunes de A y B, entonces: Sabemos que C - A esta formado por los elementos de C que no pertenecen a A, entonces: b) Calcular: A B , C – A

13. Dados los conjuntos: P = {x Z / 2x 2 +5x-3=0 } M = { x/4 N / 4≤ x < 21 } T = { x R / (x 2 - 9)(x - 4)=0 } a) Calcular: M - ( T – P ) b) Calcular: (M T ) c) Calcular: (M U T) – P 2

14. P = { x Z / 2x 2 +5x-3=0 } Analicemos cada conjunto: 2x 2 + 5x – 3 = 0 (2x-1)(x+3)=0 2x-1=0  x = 1/2 x+3=0  x = -3 Observa que x Z , entonces: P = { -3 } M = { x/4 N / 4≤ x < 21 } Como x/4 N entonces los valores de x son : 4 ; 8 ; 12 ; 16 ; 20 pero los elementos de M se obtienen dividiendo x entre 4,por lo tanto : M = {1, 2, 3, 4, 5 } 2x – 1 + 3 x   

15. T = { x R / (x 2 - 9)(x - 4)=0 } Cada factor lo igualamos a cero y calculamos los valores de x x – 4 = 0 x = 4 x 2 – 9 = 0 x 2 = 9 x = 3 o x =-3 Por lo tanto: T = { -3,3,4 } a) Calcular: M - ( T – P ) T – P = { -3,3,4 } - { -3 } T – P = {3, 4 } M - (T –P)= {1, 2, 3, 4, 5 } - {3, 4 } M - (T –P)= {1, 2, 5 }

16. M T = {3, 4} b) Calcular: ( M T ) M T = {1, 2, 3, 4, 5 } { -3,3,4 } c) Calcular: (M U T) – P M U T = {1, 2, 3, 4, 5 } U { -3, 3, 4 } M U T = { -3, 1, 2, 3, 4, 5 } (M U T) – P = { -3, 1, 2, 3, 4, 5 } - { -3 } (M U T) – P = {1, 2, 3, 4, 5 }

17. 3 Expresar la región sombreada en términos de operaciones entre los conjuntos A,B y C. A B C A B C

18. A B C A B C A B C A B C [(A B) – C] [(B C) – A] [(A C) – B] U U

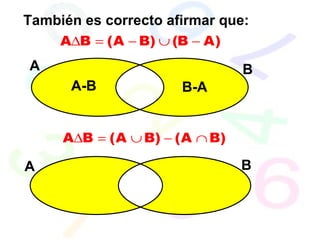
19. A B A B C Observa como se obtiene la región sombreada Toda la zona de amarillo es AUB La zona de verde es A B Entonces restando se obtiene la zona que se ve en la figura : (A U B) - (A B) C Finalmente le agregamos C y se obtiene: [ (A U B) - (A B) ] U C ( A B ) U C =

20. GRACIAS