El documento describe las funciones trigonométricas, sus dominios y rangos. Explica que el dominio de las funciones seno y coseno son todos los números reales, mientras que su rango está entre -1 y 1. El dominio de las funciones tangente y secante son todos los números reales excepto los múltiplos de π/2, y sus rangos son todos los números reales para la tangente y todos excepto entre -1 y 1 para la secante.

1. 1
I.E.E. CORONEL BOLOGNESI
Las Funciones Trigonométricas:
su dominio y su rango.
Por
Voritz Peralta Yufra
Alexander Ochoa
Profesor
Henry Villalba (Matematica)

2. Definición de función
Es una relación de dos o más variables en donde
a uno de los elementos del dominio (conjunto que
contiene todos los valores que pueden tomar la
variables independientes) corresponde uno y sólo
un elemento del rango (conjunto que contiene
todos los valores que puede tomar la variable
2
dependiente).

3. 3
Relaciones trigonométricas en triángulos rectángulos
Aunque lo común es empezar por presentar la
relaciones trigonométricas para ángulos en los
triángulos rectángulos, definidas como cocientes de
la magnitud de dos de sus lados –catetos o
hipotenusa, es posible extender su definición para
ángulos de cualquier magnitud a través del círculo
trigonométrico de radio unitario.

4. Funciones trigonométricas:
Así, cuando las relaciones trigonométricas se definen
para cualquier ángulo (sobre todo cuando se mide en
radianes, lo que en realidad es la medida del ángulo
en números reales), puede demostrarse que las
relaciones de seno, coseno, tangente, cotangente,
secante y cosecante de un ángulo, cumplen con la
definición de función. Es por ello que se les conoce
4
como funciones trigonométricas.

5. Dominio y contradominio de las funciones trigonométricas
Aunque las seis funciones trigonométricas arrojan
valores de la variable dependiente de cada una de
5
ellas, cuando se aplican a ángulos que toman
diferentes valores de la variable independiente; estas
funciones tienen dominio y rango diferentes.

6. 6
Dominio de las funciones seno y coseno de un ángulo
Como se muestra en la figura 1, en la siguiente
diapositiva, es posible definir la función seno y la
función coseno de un ángulo (x) sin importar el valor
que este ángulo tome. De manera que el dominio de
las funciones es todo el conjunto de los números
reales. Esto puede escribirse en lenguaje simbólico
como:
y = sen(x), z = cos(x)
donde x Î Â

7. Rango de las funciones seno y coseno de un ángulo
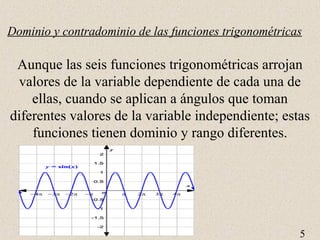
Sin embargo, la figura 1 muestra que la función seno
y la función coseno de un ángulo (x) sólo puede
tomar valores en el intervalo cerrado de –1 a 1, que
constituye el contradominio de ambas funciones.
Esto puede escribirse en lenguaje simbólico como:
7
y = sen(x) donde y Î [-1,1]
z = cos(x) donde z Î [-1,1]

8. 1.000
0.800
0.600
0.400
0.200
-0.200
-0.400
-0.600
-0.800
-1.000
8
0.000
-3p -2p -p p 2p 3p
-10 -8 -6 -4 -2 0 2 4 6 8 10
sen(x)
cos(x)
Figura 1. Funciones seno (en azul) y coseno (en rosa) del ángulo x (en radianes).

9. Características de las funciones seno y coseno de un ángulo
Característica 1. En la figura 1 (diapositiva anterior)
puede observarse el gran parecido que tienen ambas
9
funciones entre sí. De hecho, las
identidades trigonométricas
permiten asegurar que y = sen(x) = cos(x-[p/2]), lo
que también se deduce al analizar las gráficas.
Es conveniente recordar que el ángulo que mide 90º
(sexagesimales) mide [p/2] (en números reales o
radicales).

10. Características de las funciones seno y coseno de un ángulo
Característica 2. En la figura 1 también se puede
observar que los valores de ambas funciones, seno y
coseno, se repiten cíclicamente para múltiplos de 2p.
10
Esto permite escribir otras identidades
trigonométricas
de manera que:
y = sen(x) = sen(x + 2np ) siendo n elemento de
los números enteros (n Î Z), o bien
z = cos(x) = cos(x + 2np ) siendo n Î Z.

11. 11
Dominio de las funciones tangente y secante de un ángulo
Como se muestra en las figuras 2 y 3, en las
siguientes diapositivas, no siempre es posible definir
la función tangente y la función secante de un ángulo
(x). De hecho, cuando la función coseno del ángulo
toma el valor de cero, las funciones tangente y
secante no pueden definirse (¿por qué?).
En la figura 1 puede verse que esto ocurre para
ángulos que toman valores semienteros de p; lo que
simbólicamente puede expresarse como (2n+1) [p/2]
siendo n Î Z.

12. 12
Dominio de las funciones tangente y secante de un ángulo
Por lo tanto, las figuras 2 y 3, muestran que las
funciones tangente y secante
w = tan(x), v = sec(x)
tienen como dominio el conjunto de números reales
menos el conjunto de números semienteros (en donde
se dice que estas funciones son discontinuas).
xÎÂ-{±[p/2], ±[3p/2],±[5p/2],…,±(n+1)[p/2],…}
(Ver en las figuras 2 y 3 cómo es que las funciones tangente y secante
tienden a infinito o a menos infinito en los valores semienteros del
ángulo, marcados por líneas verticales que no forman parte de la
función.)

13. Rango de la función tangente de un ángulo
La figura 2 muestra que la función tangente de un
ángulo w = tan(x) puede tomar cualquier valor en el
campo de los números reales, por lo que se puede
afirmar que el contradominio de la función tangente
está formado por todos los números reales, lo que
13
simbólicamente puede escribirse como
w Î Â

14. Rango de la función secante de un ángulo
La figura 3 muestra que la función secante de un
ángulo v = sec(x) no puede tomar cualquier valor en
el campo de los números reales, porque observando
bien dicha figura la función secante nunca toma
valores comprendidos en el intervalo abierto de –1 a
14
1. Simbólicamente esto puede escribirse como
v Î Â - (-1,1)

15. 15
Ejercicio
Encontrar el dominio y el contradominio de las
funciones cotangente y cosecante de un ángulo y
explicar su respuesta.

16. 1.000
0.800
0.600
0.400
0.200
-0.200
-0.400
-0.600
-0.800
-1.000
16
0.000
-3p -2p -p p 2p 3p
-10 -8 -6 -4 -2 0 2 4 6 8 10
cot(x)
Figura 4. Función cotangente del ángulo x (en radianes).

17. 3.000
2.000
1.000
-1.000
-2.000
-3.000
17
0.000
-3p -2p -p p 2p 3p
-10 -8 -6 -4 -2 0 2 4 6 8 10
csc(x)
Figura 5. Función cosecante del ángulo x (en radianes).