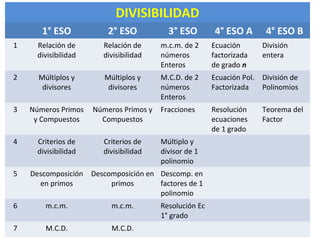
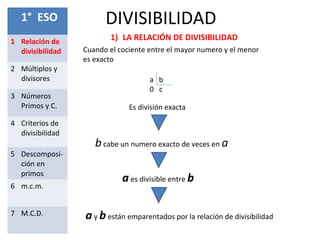
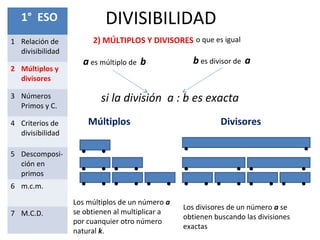
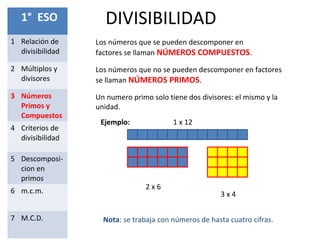
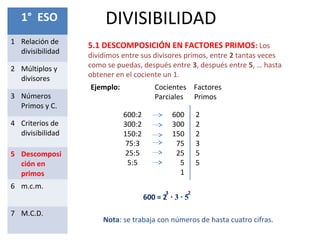
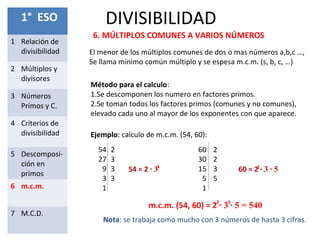
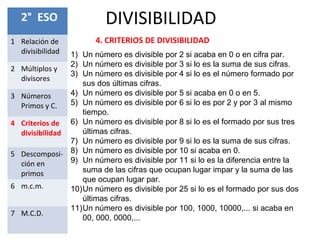
Este documento presenta los conceptos fundamentales de la divisibilidad en matemáticas. Explica la relación de divisibilidad, los múltiplos y divisores, los números primos y compuestos, los criterios de divisibilidad, la descomposición en factores primos, el mínimo común múltiplo y el máximo común divisor. El objetivo es que los estudiantes comprendan y apliquen estas nociones básicas de la divisibilidad para resolver problemas.

1. DIVISIBILIDAD
1° ESO 2° ESO 3° ESO 4° ESO A 4° ESO B
1 Relación de
divisibilidad
Relación de
divisibilidad
m.c.m. de 2
números
Enteros
Ecuación
factorizada
de grado n
División
entera
2 Múltiplos y
divisores
Múltiplos y
divisores
M.C.D. de 2
números
Enteros
Ecuación Pol.
Factorizada
División de
Polinomios
3 Números Primos
y Compuestos
Números Primos y
Compuestos
Fracciones Resolución
ecuaciones
de 1 grado
Teorema del
Factor
4 Criterios de
divisibilidad
Criterios de
divisibilidad
Múltiplo y
divisor de 1
polinomio
5 Descomposición
en primos
Descomposición en
primos
Descomp. en
factores de 1
polinomio
6 m.c.m. m.c.m. Resolución Ec
1° grado
7 M.C.D. M.C.D.

2. MÍNIMO
Reconocer si un número es múltiplo o divisor de otro número
dado. Aplicar las propiedades de los múltiplos y divisores para
resolver problemas. Utilizar los criterios de divisibilidad por 2, 3,
5, 10 y 11 en la resolución de problemas. Distinguir si un número
es primo o compuesto.
Calcular todos los divisores de un número. Fáctorizar un número.
MÁXIMO
Hallar el máximo común divisor (M.C.D.) y el mínimo común
múltiplo (m.c.m.) de dos números, descomponiéndolos en
factores primos.
Resolver problemas de la vida real en los que aparezcan
conceptos de
divisibilidad.
1° ESO
1 Relación de
divisibilidad
2 Múltiplos y
divisores
3 Números
Primos y C.
4 Criterios de
divisibilidad
5 Descomposi-
ción en
primos
6 m.c.m.
7 M.C.D.
DIVISIBILIDAD

3. DIVISIBILIDAD
1) LA RELACIÓN DE DIVISIBILIDAD
Cuando el cociente entre el mayor numero y el menor
es exacto
a b
0 c
Es división exacta
bcabe un numero exacto de veces en a
aes divisible entre b
ay bestán emparentados por la relación de divisibilidad
1° ESO
1 Relación de
divisibilidad
2 Múltiplos y
divisores
3 Números
Primos y C.
4 Criterios de
divisibilidad
5 Descomposi-
ción en
primos
6 m.c.m.
7 M.C.D.

4. DIVISIBILIDAD
2) MÚLTIPLOS Y DIVISORES
a es múltiplo de b
o que es igual
si la división a : b es exacta
b es divisor de a
Los múltiplos de un número a
se obtienen al multiplicar a
por cuanquier otro número
natural k.
Los divisores de un número a se
obtienen buscando las divisiones
exactas
Múltiplos Divisores
1° ESO
1 Relación de
divisibilidad
2 Múltiplos y
divisores
3 Números
Primos y C.
4 Criterios de
divisibilidad
5 Descomposi-
ción en
primos
6 m.c.m.
7 M.C.D.

5. DIVISIBILIDAD1° ESO
1 Relación de
divisibilidad
2 Múltiplos y
divisores
3 Números
Primos y
Compuestos
4 Criterios de
divisibilidad
5 Descomposi-
cion en
primos
6 m.c.m.
7 M.C.D.
Los números que se pueden descomponer en
factores se llaman NÚMEROS COMPUESTOS.
Los números que no se pueden descomponer en factores
se llaman NÚMEROS PRIMOS.
Un numero primo solo tiene dos divisores: el mismo y la
unidad.
1 x 12
2 x 6
3 x 4
Ejemplo:
Nota: se trabaja con números de hasta cuatro cifras.

6. DIVISIBILIDAD1° ESO
1 Relación de
divisibilidad
2 Múltiplos y
divisores
3 Numeros
Primos y C.
4 Criterios de
divisibilidad
5 Descomposi-
ción en
primos
6 m.c.m.
7 M.C.D.
MULTIPLO DE 2: Un número es múltiplo de 2 si
termina en cifra par: 0,2,4,6,8.
MULTIPLO DE 3: Un número es múltiplo de 3 si las
suma de sus cifras es múltiplo de 3.
MULTIPLO DE 5: Un número es múltiplo de 5 si termina
por 0 o 5.
MULKTIPLO DE 10: Un número es múltiplo de 10 si
termina por la cifra 0.
Nota: se trabaja con números de hasta cuatro cifras.
Ejemplo: Busca entre estos números los múltiplos de 2,
los de 3, los de 5, los de 7, los de 13.
104, 130, 140, 119, 143, 182
186, 147, 200, 255, 245, 203
4. CRITERIO DE DIVISIBILIDAD

7. DIVISIBILIDAD1° ESO
1 Relación de
divisibilidad
2 Múltiplos y
divisores
3 Números
Primos y C.
4 Criterios de
divisibilidad
5 Descomposi
ción en
primos
6 m.c.m.
7 M.C.D.
Nota: se trabaja con números de hasta cuatro cifras.
5.1 DESCOMPOSICIÓN EN FACTORES PRIMOS: Los
dividimos entre sus divisores primos, entre 2 tantas veces
como se puedas, después entre 3, después entre 5, … hasta
obtener en el cociente un 1.
Ejemplo: Cocientes Factores
Parciales Primos
600
300
150
75
25
5
1
2
2
2
3
5
5
600:2
300:2
150:2
75:3
25:5
5:5
600 = 2 ∙ 3 ∙ 5
3 2

8. DIVISIBILIDAD1° ESO
1 Relación de
divisibilidad
2 Múltiplos y
divisores
3 Números
Primos y C.
4 Criterios de
divisibilidad
5 Descomposi
ción en
primos
6 m.c.m.
7 M.C.D.
Nota: se trabaja con números de hasta cuatro cifras.
5.2 MULTIPLOS Y DIVISORES de números descompuestos en
factores primos
Ejemplo 1: dado un numero descompuesto en factores primos
buscar sus múltiplos por 2, 3 y 5
40 ∙ 5 = 200 = 2 ∙ 2 ∙ 2 ∙ 5 ∙ 5
Los múltiplos de un numero contienen todos los factores
primos de ese numero.
40
Ejemplo 2:
40 : 4 = 10 → 2 ∙ 2 ∙ 2 ∙ 5 = 4 ∙ 10
Los divisores de un numero contienen algunos de los factores
primos de ese numero.

9. DIVISIBILIDAD1° ESO
1 Relación de
divisibilidad
2 Múltiplos y
divisores
3 Números
Primos y C.
4 Criterios de
divisibilidad
5 Descomposi-
ción en
primos
6 m.c.m.
7 M.C.D.
Nota: se trabaja como mucho con 3 números de hasta 3 cifras.
6. MÚLTIPLOS COMUNES A VARIOS NÚMEROS
El menor de los múltiplos comunes de dos o mas números a,b,c …,
Se llama mínimo común múltiplo y se espesa m.c.m. (s, b, c, …)
Método para el calculo:
1.Se descomponen los numero en factores primos.
2.Se toman todos los factores primos (comunes y no comunes),
elevado cada uno al mayor de los exponentes con que aparece.
Ejemplo: calculo de m.c.m. (54, 60):
54
27
9
3
1
2
3
3
3
60
30
15
5
1
2
2
3
5
54 = 2 ∙ 33
60 = 2 ∙ 3 ∙ 52
m.c.m. (54, 60) = 2 ∙ 3 ∙ 5 = 5402 3

10. DIVISIBILIDAD1° ESO
1 Relación de
divisibilidad
2 Múltiplos y
divisores
3 Números
Primos y C.
4 Criterios de
divisibilidad
5 Descomposi-
ción en
primos
6 m.c.m.
7 M.C.D.
Nota: se trabaja como mucho con 3 números de hasta 3 cifras.
El mayor de los divisores comunes a 2, o mas números, a, b, c, …, se
llama MÁXIMO COMÚN DIVISORES y se expresa M.C.D. (a, b, c, …).
Calculo de M.C.D.:
1.Se descompones los números en factores primos.
2.Se toman solamente los factores primos comunes,
elevado cada uno al menor exponente con el que aparece.
Ejemplo: Calculo de M.C.D. (60, 100).
60
30
15
5
1
2
2
3
5
100
50
25
5
1
2
2
5
5
60 = 2 ∙ 3 ∙ 52
100 = 2 ∙ 52 2
M.C.D. (60, 100) = 2 ∙ 5 = 202

11. DIVISIBILIDAD2° ESO
1 Relación de
divisibilidad
2 Múltiplos y
divisores
3 Números
Primos y C.
4 Criterios de
divisibilidad
5 Descomposi-
ción en
primos
6 m.c.m.
7 M.C.D.
OBJETIVOS MÍNIMOS
a) Reconocer si un número es múltiplo o divisor de
otro.
b) Conocer y aplicar los criterios de divisibilidad.
c) Aplicar procedimientos óptimos para descomponer
un número en factores primos.
d) Conocer y aplicar los algoritmos óptimos para
calcular el M.C.D. y el m.c.m. de dos o más
números.
e) Resolver problemas apoyándose en el concepto de
m.c.m
f) Resolver problemas apoyándose en el concepto de
M.C.D.

12. DIVISIBILIDAD
Ej: 390:15
390 15
90 26
0
Es división exacta
390es divisible entre 15
2° ESO
1 Relación de
divisibilidad
2 Múltiplos y
divisores
3 Números
Primos y C.
4 Criterios de
divisibilidad
5 Descomposi-
ción en
primos
6 m.c.m.
7 M.C.D.
1) Decimos que un número b es divisible
entre otro a (distinto de cero) si existe un
tercer entero c tal que b = a · c

13. DIVISIBILIDAD
2. MÚLTIPLOS Y DIVISORES: PROPIEDADES
2° ESO
1 Relación de
divisibilidad
2 Múltiplos y
divisores
3 Números
Primos y C.
4 Criterios de
divisibilidad
5 Descomposi-
ción en
primos
6 m.c.m.
7 M.C.D.

14. DIVISIBILIDAD2° ESO
1 Relación de
divisibilidad
2 Múltiplos y
divisores
3 Números
Primos y
Compuesto
4 Criterios de
divisibilidad
5 Descomposi-
ción en
primos
6 m.c.m.
7 M.C.D.
Los números que se pueden descomponer en
factores se llaman NÚMEROS COMPUESTOS.
Los números que no se pueden descomponer en factores
se llaman NÚMEROS PRIMOS.
Un numero primo solo tiene dos divisores: el mismo y la
unidad.
Ejemplo:
 6: Número compuesto
 2: Número primo
 3: Número primo

15. DIVISIBILIDAD2° ESO
1 Relación de
divisibilidad
2 Múltiplos y
divisores
3 Números
Primos y C.
4 Criterios de
divisibilidad
5 Descomposi-
ción en
primos
6 m.c.m.
7 M.C.D.
4. CRITERIOS DE DIVISIBILIDAD
1) Un número es divisible por 2 si acaba en 0 o en cifra par.
2) Un número es divisible por 3 si lo es la suma de sus cifras.
3) Un número es divisible por 4 si lo es el número formado por
sus dos últimas cifras.
4) Un número es divisible por 5 si acaba en 0 o en 5.
5) Un número es divisible por 6 si lo es por 2 y por 3 al mismo
tiempo.
6) Un número es divisible por 8 si lo es el formado por sus tres
últimas cifras.
7) Un número es divisible por 9 si lo es la suma de sus cifras.
8) Un número es divisible por 10 si acaba en 0.
9) Un número es divisible por 11 si lo es la diferencia entre la
suma de las cifras que ocupan lugar impar y la suma de las
que ocupan lugar par.
10)Un número es divisible por 25 si lo es el formado por sus dos
últimas cifras.
11)Un número es divisible por 100, 1000, 10000,... si acaba en
00, 000, 0000,...

16. DIVISIBILIDAD2° ESO
1 Relación de
divisibilidad
2 Múltiplos y
divisores
3 Números
Primos y C.
4 Criterios de
divisibilidad
5 Descomposi
ción en
primos
6 m.c.m.
7 M.C.D.
5.1 DESCOMPOSICIÓN EN FACTORES PRIMOS: Los
dividimos entre sus divisores primos, entre 2 tantas veces
como se puedas, después entre 3, después entre 5, … hasta
obtener en el cociente un 1.
Ejemplo: Cocientes Factores
Parciales Primos
600
300
150
75
25
5
1
2
2
2
3
5
5
600:2
300:2
150:2
75:3
25:5
5:5
600 = 2 ∙ 3 ∙ 5
3 2

17. DIVISIBILIDAD2° ESO
1 Relación de
divisibilidad
2 Múltiplos y
divisores
3 Números
Primos y C.
4 Criterios de
divisibilidad
5 Descomposi
ción en
primos
6 m.c.m.
7 M.C.D.
5.2 MÚLTIPLOS Y DIVISORES de números descompuestos en
factores primos
Ejemplo 1: dado un numero descompuesto en factores primos
buscar sus múltiplos por 2, 3 y 5
40 ∙ 5 = 200 = 2 ∙ 2 ∙ 2 ∙ 5 ∙ 5
Los múltiplos de un numero contienen todos los factores
primos de ese numero.
40
Los divisores de un numero contienen algunos de los factores
primos de ese numero.
Ejemplo 2:
40 : 4 = 10 → 2 ∙ 2 ∙ 2 ∙ 5 = 4 ∙ 10

18. DIVISIBILIDAD2° ESO
1 Relación de
divisibilidad
2 Múltiplos y
divisores
3 Números
Primos y C.
4 Criterios de
divisibilidad
5 Descomposi-
ción en
primos
6 m.c.m.
7 M.C.D.
6. MULTIPLOS COMUNES A VARIOS NUMEROS
El menor de los múltiplos comunes de dos o mas números a,b,c …,
Se llama mínimo común múltiplo y se espesa m.c.m. (s, b, c, …)
Método para el calculo:
1.Se descomponen los numero en factores primos.
2.Se toman todos los factores primos (comunes y no comunes),
elevado cada uno al mayor de los exponentes con que aparece.
Ejemplo: calculo de m.c.m. (54, 60):
54
27
9
3
1
2
3
3
3
60
30
15
5
1
2
2
3
5
54 = 2 ∙ 33
60 = 2 ∙ 3 ∙ 52
m.c.m. (54, 60) = 2 ∙ 3 ∙ 5 = 5402 3

19. DIVISIBILIDAD2° ESO
1 Relación de
divisibilidad
2 Múltiplos y
divisores
3 Números
Primos y C.
4 Criterios de
divisibilidad
5 Descomposi-
ción en
primos
6 m.c.m.
7 M.C.D.
7. El MAYOR de los divisores comunes a 2, o mas números, a, b, c, …, se
llama MÁXIMO COMÚN DIVISOR y se expresa M.C.D. (a, b, c, …).
Calculo de M.C.D.:
1.Se descomponen los números en factores primos.
2.Se toman solamente los factores primos comunes,
elevado cada uno al menor exponente con el que aparece.
Ejemplo: Calculo de M.C.D. (60, 100).
60
30
15
5
1
2
2
3
5
100
50
25
5
1
2
2
5
5
60 = 2 ∙ 3 ∙ 52
100 = 2 ∙ 52 2
M.C.D. (60, 100) = 2 ∙ 5 = 202

20. DIVISIBILIDAD
M.C.D. y m.c.m. de dos números enteros
Múltiplos y divisores de un polinomio
Descomposiciones en factores de un polinomio
Resolución de ecuaciones de primer grado
(1 paso: quitar denominadores con el m.c.m.;
2 paso: Eliminar paréntesis;
3 paso transponer términos;
4 paso: reducir términos;
5 términos despeja la incógnita)
3° ESO
1 m.c.m. de 2
números
Enteros
2 M.C.D. de 2
números
Enteros
3 Fracciones
4 Multiplo y
divisore de 1
polinomio
5 Descomp. en
factores de 1
polinomio
6 Resolución
Ecuación de
1° grado

21. DIVISIBILIDAD
1. M.C.M. DE 2 NÚMEROS ENTERO:
Es igual al de sus valores absolutas.
Se obtiene descomponiendo los números
en factores primos y multiplicando los
factores comunes y no comunes
elevados al MAYOR exponente
Ejemplo:
m.c.m. ( -18, 42 ) =
=m.c.m. (| -18 |, | 42 |) =
=m.c.m. ( 18, 42 ) =
= m.c.m.( 2 ∙ 3 ∙ 3 , 2 ∙ 3 ∙ 7 ) =
= 2 ∙ 3 ∙ 3 ∙ 7 = 126
3° ESO
1 m.c.m. de 2
números
Enteros
2 M.C.D. de 2
números
Enteros
3 Fracciones
4 Multiplo y
divisore de 1
polinomio
5 Descomp. en
factores de 1
polinomio
6 Resolución
Ecuación de
1° grado

22. DIVISIBILIDAD3° ESO
1 m.c.m. de 2
números
Enteros
2 M.C.D. de 2
números
Enteros
3 Fracciones
4 Multiplo y
divisore de 1
polinomio
5 Descomp. en
factores de 1
polinomio
6 Resolución
Ecuación de
1° grado
2. M.C.D. DE 2 NÚMEROS ENTERO:
Es igual al de sus valores absolutas.
Se obtiene descomponiendo los números
en factores primos y multiplicando los
factores comunes elevados al MENOR exponente
Ejemplo:
M.C.D. ( -18, 42 ) =
= M.C.D. (| -18 |, | 42 |) =
= M.C.D. ( 18, 42 ) =
= M.C.D.( 2 ∙ 3 ∙ 3 , 2 ∙ 3 ∙ 7 ) =
= 2 ∙ 3 = 6

23. DIVISIBILIDAD3° ESO
1 m.c.m. de 2
números
Enteros
2 M.C.D. de 2
números
Enteros
3 Fracciones
4 Multiplo y
divisore de 1
polinomio
5 Descomp. en
factores de 1
polinomio
6 Resolución
Ecuación de
1° grado
3. FRACCIONES: Expresión a/b en la que a y b
son números entero.
3.1 REDUCCION A COMUN DENOMINADOR: Se calcula el m.c.m. de los
denominadores que será el denominador de las fracciones equivalente.
3.2 SUMAS Y RESTA DE FRACCIÓNES: Se reducen a común
denominador
y después se suman y se restan
3.3 SIMPLIFICACION DE FRACCIONES: para simplificar las fracciones
usamos M.C.D. para obtener una fracción irreducible.
Ejemplo:
3 4 2 3 12 10 3 + 12 - 10
15 5 3 15 15 15 15
=5/15=1/3.

24. DIVISIBILIDAD3° ESO
1 m.c.m. de 2
números
Enteros
2 M.C.D. de 2
números
Enteros
3 Fracciones
4 Multiplo y
divisore de 1
polinomio
5 Descomp. en
factores de 1
polinomio
6 Resolución
Ecuación de
1° grado
4. MULTIPLO Y DIVISORE DE 1 POLINOMIO:
Si tenemos los Polinomio P(x) y Q(x) y los dividimos,
obtenemos otros dos polinomios C(x) y R(x), tales que
P(x)=Q(x) ∙ C(x) + R(x).
Si R(x)=0, la división es exacta y el polinomio P(x) es divisible por Q(x).
Ejemplo:
( x3
- 3x2
+ 2x ) : x = x2
- 3x + 2
• ( x3
- 3x2
+ 2x ) es divisible por x
• ( x3
- 3x2
+ 2x ) es múltiplo de x
• X es divisor de ( x3
- 3x2
+ 2x )
Nota: El grado de los monomio son potencias de una cifra.

25. DIVISIBILIDAD3° ESO
1 m.c.m. de 2
números
Enteros
2 M.C.D. de 2
números
Enteros
3 Fracciones
4 Multiplo y
divisore de 1
polinomio
5 Descompos.
en factores
6 Resolución
Ecuación de
1° grado
5. DESCOMPOSICIÓN EN FACTORES DE LA DIFERENCIA
DE DOS CUADRADOS:
( a2
- b2
) = ( a + b )(a - b )

26. DIVISIBILIDAD3° ESO
1 m.c.m. de 2
números
Enteros
2 M.C.D. de 2
números
Enteros
3 Fracciones
4 Multiplo y
divisore de 1
polinomio
5 Descompos.
en factores
6 Resolución
Ecuación de
1° grado
6. RESOLUCIÓN ECUACIÓN DE 1° GRADO:
1 paso: quitar denominadores
con el m.c.m.
2 paso: Eliminar paréntesis,
3 paso transponer términos.
4 paso: reducir términos
5 paso: despeja la incógnita
( )
3
82
4
13 +
=
−− xxx
( )
( )( ) ( )824133
3
82
12
4
13
12
+=−−
+
⋅=
−−
⋅
xxx
xxx
( )
328339
328133
+=+−
+=+−
xxx
xxx
332839 −=−− xxx
292 =− x
2
29
−=x

27. DIVISIBILIDAD4° ESOA
1A División de
monomios
y de
polinomios
2A Fracción
irreducible
3A Resolución
de
ecuaciones
de 1 grado
1A. DIVISIÓN DE MONOMIOS:
( ) ( ) nm
n
m
nm
x
b
a
bx
ax
bxax −
==:
DIVISIÓN DE POLINOMIOS:
( ) ( ) ( ) ( )xRxCxQxP +⋅=
Si R(x)=0 la división es exacta
32
3253
99811476 2
34
23456
+−=
+−+
+−++++
xx
xxx
xxxxxx
EJEMPLO:

28. DIVISIBILIDAD4° ESOA
1A División de
monomios
y de
polinomios
2A Fracción
irreducible
3A Resolución
de
ecuaciones
de 1 grado
2A. FRACCIÓN IRREDUCIBLE:
( )
( )
( ) ( )
( ) ( )
( )
( )xQ
xP
xDxQ
xDxP
xQ
xP
1
1
=
⋅
⋅
=
D(x) es el M.C.D. de P(x) y Q(x) por lo tanto obtenemos una
Fracción irreducible:

29. DIVISIBILIDAD
3A. RESOLUCIÓN ECUACIÓN DE 1° GRADO:
1 paso: quitar denominadores
con el m.c.m.
2 paso: Eliminar paréntesis,
3 paso transponer términos.
4 paso: reducir términos
5 paso: despeja la incógnita
( )
3
82
4
13 +
=
−− xxx
( )
( )( ) ( )824133
3
82
12
4
13
12
+=−−
+
⋅=
−−
⋅
xxx
xxx
( )
328339
328133
+=+−
+=+−
xxx
xxx
332839 −=−− xxx
292 =− x
2
29
−=x
4° ESOA
1A Ecuación
factorizadas
con factores
de grado n
2A Ecuación
Polifónicas
que pueden
factorizarse
3A Resolución
de
ecuaciones
de 1 grado

30. DIVISIBILIDAD4° ESO B
1B División
entera
2B División de
Polinomios
3B Teorema del
Factor
1B. DIVISIÓN ENTERA:
En general:
Dividendo = Divisor ∙ Cociente + Resto
D = d ∙ C + R
Si R es cero la división es exacta :
• D es divisible por d o múltiplo de d.
• d es un factor de D o un divisor de D.

31. DIVISIBILIDAD4° ESO B
1B División
entera
2B División de
Polinomios
3B Teorema del
Factor
2B. DIVISIÓN DE POLINOMIO:
En general:
Dividendo = Divisor ∙ Cociente + Resto
D (x)= d(x) ∙ C(x) + R(x)
Si R(x) es cero la división es exacta :
• D(x) es divisible por d(x) o múltiplo de d(x).
• d(x) es un factor de D(x) o un divisor de D(x).

32. DIVISIBILIDAD4° ESO B
1B División
entera
2B División de
Polinomios
3B Teorema del
Factor
3B. TEOREMA DEL FACTOR:
P(x) = (x-a)∙C(x)
Un polinomio tiene como factor x-a si el valor numérico
de dicho polinomio para x=a es cero.
EJEMPLO:
( )( )431272
−−=+− xxxx