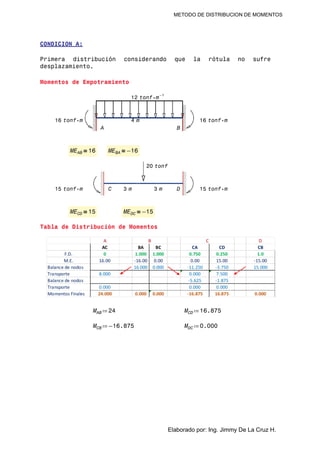
Este documento presenta la solución al análisis de una viga mediante el método de distribución de momentos. Se calculan las rigideces de las secciones, los factores de distribución, los momentos de empotramiento y las fuerzas internas para dos condiciones: considerando que la rótula no se desplaza y suponiendo un pequeño desplazamiento en un punto. Finalmente, se verifica el equilibrio estático de las dos situaciones.

1. METODO DE DISTRIBUCION DE MOMENTOS
Ejemplo 11:
Analice la viga mostrada en la figura por el metodo de distribución
de momento
⋅12 tonf m
-1
20 tonf ＝EI cte
D
A 4 m B 2 m C 3 m 3 m
Solución:
Rótula
1. Rigidez:
≔KAB =―
3
4
―
1
4
0.188
≔KBC =⋅―
3
4
―
1
2
0.375
≔KCD =⋅―
3
4
―
1
6
0.125
2. Factor de Distribución:
≔FDAB 0
≔FDBA 1
≔FDBC 1
≔FDCB =―――
KBC
+KBC KCD
0.75
≔FDCD =―――
KCD
+KBC KCD
0.25
≔FDCB 1
Elaborado por: Ing. Jimmy De La Cruz H.

2. METODO DE DISTRIBUCION DE MOMENTOS
CONDICION A:
Primera distribución considerando que la rótula no sufre
desplazamiento.
Momentos de Empotramiento
⋅12 tonf m
-1
⋅16 tonf m 4 m ⋅16 tonf m
A B
＝MEAB 16 ＝MEBA -16
20 tonf
⋅15 tonf m C 3 m 3 m D ⋅15 tonf m
＝MECD 15 ＝MEDC -15
Tabla de Distribución de Momentos
≔MAB 24 ≔MCD 16.875
≔MCB -16.875 ≔MDC 0.000
Elaborado por: Ing. Jimmy De La Cruz H.

3. METODO DE DISTRIBUCION DE MOMENTOS
Calculo de Fuerzas Internas
⋅12 tonf m
-1
24 A B C 16.875
A
4.00 m 2.00 m
Ay Cy1
＝∑MB 0
＝-⋅Cy1 2 16.875 0 ＝-+24 ⋅⋅12 4 2 ⋅Ay 4 0
≔Cy1 ―――
16.875
2
≔Ay ―――――
+24 ⋅⋅2 12 4
4
=Cy1 8.44 =Ay 30
20 v
C D
16.875 0
6 m
Cy2 Dy
＝∑MB 0
＝-+⋅Dy 6 16.875 ⋅20 3 0
≔Dy ――――――
+-16.875 ⋅20 3
6
=Dy 7.19
＝∑Fy 0
＝-+Cy2 Dy 20 0
≔Cy2 -20 Dy
=Cy2 12.81
Reacciones en los apoyos:
≔RA =Ay 30
≔RC =+Cy1 Cy2 21.25
≔RD =Dy 7.19
Elaborado por: Ing. Jimmy De La Cruz H.

4. METODO DE DISTRIBUCION DE MOMENTOS
CONDICION B:
Suponiendo que el punto B se desplaza un 1.00 cm, calculamos los
momentos de empotramientos.
A 4 m B 2 m C
Δ MECB
MEAB MEBA MEBC
≔EI 1000 ≔Δ 0.01
≔MEAB =―――
⋅⋅6 EI Δ
4
2
3.75
≔MEBA =―――
⋅⋅6 EI Δ
4
2
3.75
≔MEBC =―――
⋅-6 EI Δ
2
2
-15
≔MECB =―――
⋅-6 EI Δ
2
2
-15
Tabla de Distribución de Momentos
≔M'AB 1.875 ≔M'CD 1.875
≔M'CB -1.875 ≔M'DC 0.000
Elaborado por: Ing. Jimmy De La Cruz H.

5. METODO DE DISTRIBUCION DE MOMENTOS
Calculo de Fuerzas Internas
A B C
1.875 4.00 m 2.00 m 1.875
A'y C'y1
＝∑MB 0
＝-⋅C'y1 2 1.875 0＝-⋅A'y 4 1.875 0
≔C'y1 ―――
1.875
2
≔A'y ―――
1.875
4
=C'y1 0.938=A'y 0.469
C 6 m D
0.000
1.875
C'y2 D'y
＝∑MC 0＝∑MD 0
＝+⋅D'y 6 1.875 0＝+⋅-C'y2 6 1.875 0
≔D'y ―――
-1.875
6
≔C'y2 ―――
1.875
6
=D'y -0.313=C'y2 0.313
Reacciones en los apoyos:
≔R'A =A'y 0.469
≔R'C =+C'y1 C'y2 1.25
≔R'D =D'y -0.313
Ecuación de Condición
Para las situaciones A y B superpuestas debe cumplirse la
ecuación de equilibrio estático:
＝-+⎛⎝ ++RA RC RD
⎞⎠ ⋅⎛⎝ ++R'A R'C R'D
⎞⎠ r 68 0
≔r ――――――
-68 ⎛⎝ ++RA RC RD
⎞⎠
⎛⎝ ++R'A R'C R'D
⎞⎠
=r 6.8
Elaborado por: Ing. Jimmy De La Cruz H.

6. METODO DE DISTRIBUCION DE MOMENTOS
Momentos Finales
≔MfAB =+MAB ⋅M'AB r 36.75
≔MfCB =+MCB ⋅M'CB r -29.63
≔MfCD =+MCD ⋅M'CD r 29.63
≔MfDC =+MDC ⋅M'DC r 0
Fuerzas Cortantes Finales
≔Afy =+Ay ⋅A'y r 33.19
≔Cfy1 =+Cy1 ⋅C'y1 r 14.81
≔Cfy2 =+Cy2 ⋅C'y2 r 14.94
≔Dfy =+Dy ⋅D'y r 5.06
Diagrama de Fuerza Cortante
14.81 5.06
33.19 14.94
Diagrama de Momento Flector
36.75
8.81
29.63
Elaborado por: Ing. Jimmy De La Cruz H.