Una turbina Pelton opera bajo una altura neta de 240m. Se determina la fuerza tangencial del chorro sobre las cucharas, la potencia desarrollada, el rendimiento hidráulico y global, y la potencia útil. La fuerza tangencial es de 73.564,298 N. La potencia desarrollada es de 2.225 KW. El rendimiento hidráulico es de 79.6% y el rendimiento global es de 77.2%. La potencia útil en el eje es de 2.934,835 CV.

1. UNIVERSIDAD “FERMIN TORO
VICE RECTORADO ACADEMICO
FACULTAD DE INGENIERIA
ESCUELA DE INGENERIA EN MANTENIMIENTO MECANICO
Estudiante:
Felix Velásquez 26.267.439
CABUDARE, SEPTIEMBRE 2016
EJERCICIO PRÁCTICO N° 2

2. Problema
Una turbina Pelton trabaja bajo una altura neta de 240m. Sus
características son: Coeficiente de tobera es (φ) igual a 0,98;
Kc1u = 0,45; y un Ku1 = 0,70; un ángulo α1 = 0, un ángulo
β2 = 15º ; u1 = 0,45 c1; w2 = 0,70 w1; diámetro del chorro
ds = 150 mm.; diámetro medio de la rueda: D = 1.800 mm.
Determinar:
a) La fuerza tangencial ejercida por el chorro sobre las cucharas
b) La potencia desarrollada por la turbina
c) El rendimiento hidráulico
d) El rendimiento global, siendo: ηmec= 0,97; ηvol = 1
e) La potencia útil en el eje de la máquina

3. Datos
 Hneta = 240 m.
 β2 =15º α1 = 0º
 ϕ = 0, 98
 w2 = ku1 . w1
 ku1 = 0, 70⇒w2 = 0, 70 . w1
 kc1u = 0, 45
 u1 = 0, 45. c1
 dS =150 mm.
 D =1.800 mm.

4. Solución del problema
Antes de buscar la fuerza tangencial ejercida por el chorro
sobre las cucharas, se procede a resolver los triángulos de
velocidad y luego aplicar ecuación:
Fch = Q . Y . (w1u − w2u ) A
g
? ? ?

5. a) Triángulos de velocidades:
Entrada:
c1 =ϕ . 2. g . Hn
C1 = 0, 98. 2 . (9,81ms2 ) . (240 m)
U1 = u2 = u
  
C1 = 67, 248 m/s
u1 = kcu1 . c1
u1 = 0, 45. 2.g.Hneta
u1 = 0, 45. 67, 248 m/s
u1 = 30, 262 m/s
w1 = w1u
w1u = c1 − u1
w1u = (67, 248− 30, 262) m/s
w1u = 36, 986 m/s
α1=0; Β1= 0
w1
→
u1
→
U1 = u2 = u
→
→ →
c1
→

6. a) Triángulos de velocidades:
Salida
u2 = u1 = 30, 25 m/s
w2 = ku1 x w1
w2 = 0,70 x 36, 986 m/s w2 = 25,89 m/s
c
2 = (u
2)
2+ (w
2)
2− 2 . u
2 . w
2 . cosβ2
c2= (30, 25)2 + (25,89)2 − 2 x [(30, 25 x 25,89 x cos 15° )]
c
2 = 8, 51 m/s
w2u = − w2 . Cos β2
w2u = − 25,89 m/s. Cos 15° w2u = − 25 m/s
senα2 =25,89. sen15º
8, 51
senα2 = 0, 787
W 2 senβ2 = c2 senα2 ⇒ senα2 = w 2 .senβ2
c2
α2 = 51, 9º
------------
w2
→ →
c2
u2
→
α2
β2

7. Por otra parte, se procede a buscar el caudal Q:
Q = c1 . . dS 2
4
Q = 67, 248 m .  . (0,150 m)2
s 4 Q =1,188 m3
s
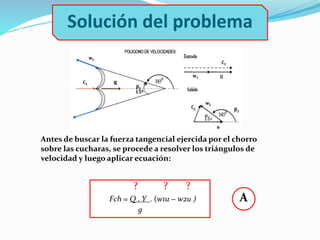
a) La fuerza tangencial Fch ejercida por el chorro sobre las cucharas:
(Sustituimos valores en la ecuación):
Fch = Q. γ .(w1u − w2u )
g
A
Ahora procedo a sustituir valores obtenidos en la ecuación: cos β1 =1 cos β2 =1
Fch =1,188 m3/s. 1.000kgf / m3 . [(36, 986 −(−25)]m/s
9,81 m /s2
Fch = 7.506, 561 kgf
Multiplico por 9,8 para llevarlo a Newton: Fch = 73.564, 298 N

8. b) La potencia desarrollada por la turbina(potencia efectiva):
Dividir entre 735,5 para llevarlo a CV:
Se procede a buscar la altura teórica Hu:
Pefect = Fch x u Pefect = 73.564, 298 N x 30, 25m/s
Pefect= 2.225.320, 008 N .m
s
Pefect = 2.225 Kw
Pefect = 3.027, 646 CV
C) El rendimiento hidráulico ηh : Hid = Hu
H
Hu = Pi / Q.  . g Hu = ____2.225.000 kg.m 2/s 3 ___
1,188 m3. 1000 kg . 9,81m
s m3 s 2
Hu =191m.
A
?

9. Ahora, sustituyo valores en: ηHid
d) El rendimiento global, siendo:
Suponiendo un rendimiento volumétrico igual a la unidad:
e) Potencia útil en el eje de la maquina (La potencia útil se conoce
también como potencia al freno):
Hid = 191 m
240 m Hid = 0, 796
Hid = 79, 6%
Total = Vol . Mec . Hid
Vol =1
Total = 0, 97 x 0, 796 Total = 0, 772 Total = 77, 2%
Pfre = γ x Q x Hneta x ηTotal
75
Pfre = 1.000kg/m 3 x 1,188m 3/s x 240m x 0, 772
75
Pfre = 2.934,835CV