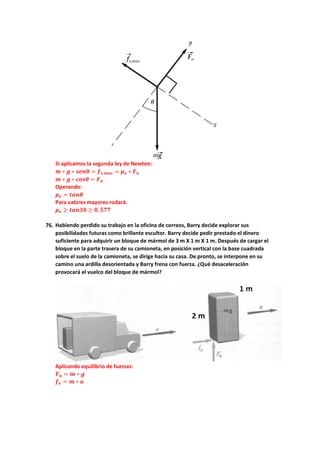
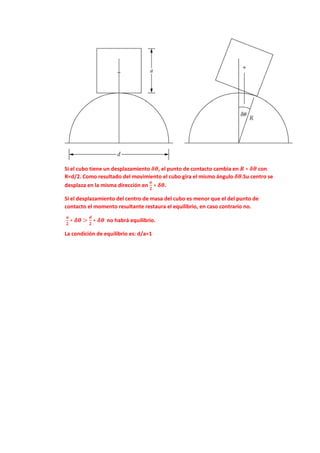
Este documento discute los conceptos de equilibrio estático y elasticidad, centro de gravedad y fuerzas. Explica las condiciones para que exista equilibrio estático, como la suma de fuerzas y momentos resultantes deben ser cero. También presenta varios ejemplos numéricos que ilustran cómo calcular fuerzas desconocidas aplicando estas condiciones de equilibrio.




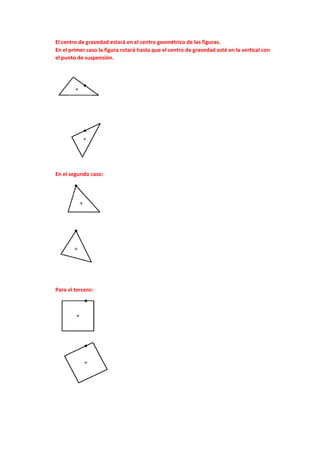











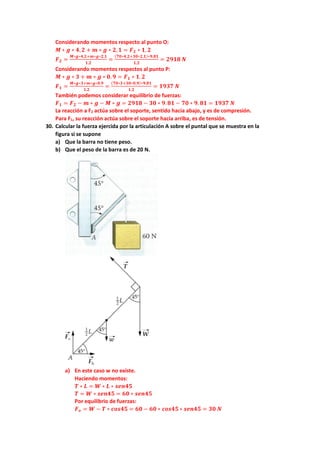






















![Para tener equilibrio rotacional debemos tener momento nulo. El momento respecto
al centro es:
𝑴𝑴𝟏𝟏 ∗ 𝒈𝒈 ∗ 𝑹𝑹𝟏𝟏 = 𝑴𝑴𝟐𝟐 ∗ 𝒈𝒈 ∗ 𝑹𝑹𝟐𝟐
Eso se cumple en el caso c.
68. ¿Cuál de las siguientes magnitudes podría n tener unidades de N/m2
?
a) Módulo de Young.
b) Módulo de cizalladura.
c) Tensión.
d) Deformación.
El módulo de Young es:
𝒀𝒀 =
𝑻𝑻/𝑨𝑨
∆𝑳𝑳/𝑳𝑳
Las unidades S.I.:
[𝒀𝒀] =
𝑵𝑵/𝒎𝒎𝟐𝟐
𝒎𝒎/𝒎𝒎
=
𝑵𝑵
𝒎𝒎𝟐𝟐
[𝑴𝑴𝒔𝒔] = �
𝑭𝑭𝒔𝒔/𝑨𝑨
𝒕𝒕𝒕𝒕𝒕𝒕
� =
𝑵𝑵
𝒎𝒎𝟐𝟐
[𝑻𝑻𝑻𝑻𝑻𝑻𝑻𝑻𝑻𝑻ó𝒏𝒏] = [𝑭𝑭/𝑨𝑨] =
𝑵𝑵
𝒎𝒎𝟐𝟐
[𝑫𝑫𝑫𝑫𝑫𝑫𝑫𝑫𝑫𝑫𝑫𝑫𝑫𝑫𝑫𝑫𝑫𝑫ó𝒏𝒏] = 𝒕𝒕𝒕𝒕𝒕𝒕
Este último no tiene dimensiones de
𝑵𝑵
𝒎𝒎𝟐𝟐.
69. Una persona está sentada en una silla con la espalda erecta. Si intenta levantarse sin
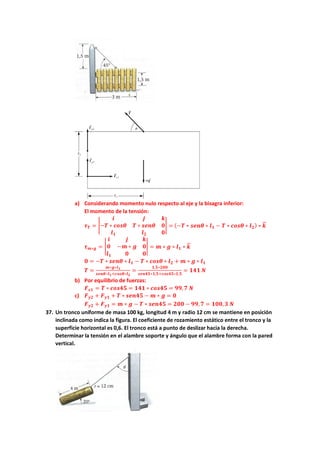
inclinarse hacia delante no puede hacerlo. ¿Por qué?
El centro de gravedad está sobre sus pies, para levantarse el centro de seguridad debe
estar por delante de sus pies y tener un momento resultante.
70. Un tablero de 90 N que tiene una longitud de 12 m está apoyado en dos soportes, cada
uno de los cuales dista 1 m del extremo del tablero. Se coloca un bloque de 360 N sobre
el tablero a 3 m de un extremo, como se indica en la figura. Hallar la fuerza ejercida por
cada soporte sobre el tablero.
Tomando momentos respecto al soporte de la derecha:
𝑵𝑵𝒊𝒊 ∗ 𝟏𝟏𝟏𝟏 = 𝟗𝟗𝟗𝟗 ∗ 𝟒𝟒 + 𝟑𝟑𝟑𝟑𝟑𝟑 ∗ 𝟐𝟐 ; 𝑵𝑵𝒊𝒊 =
𝟗𝟗𝟗𝟗∗𝟓𝟓+𝟑𝟑𝟑𝟑𝟑𝟑∗𝟐𝟐
𝟏𝟏𝟏𝟏
= 𝟏𝟏𝟏𝟏𝟏𝟏 𝑵𝑵
Por equilibrio de fuerzas:](https://image.slidesharecdn.com/equilibrioestticoyelasticidad-220312080447/85/Equilibrio-estatico-y-elasticidad-41-320.jpg)