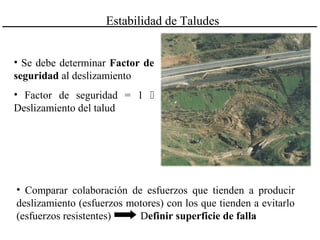
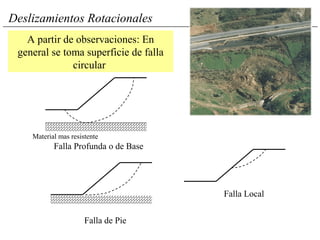
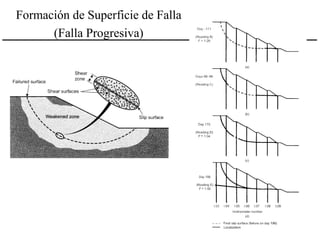
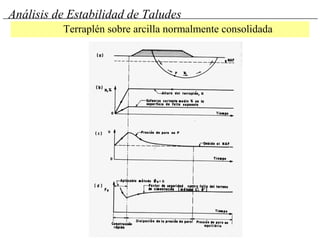
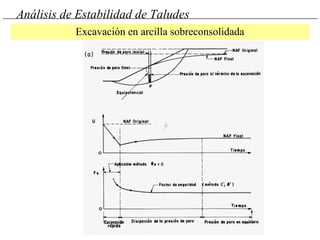
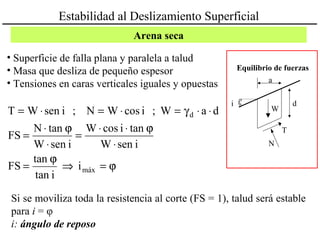
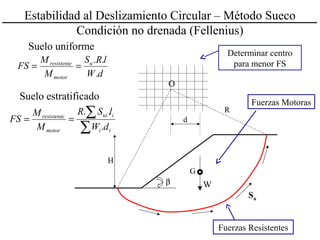
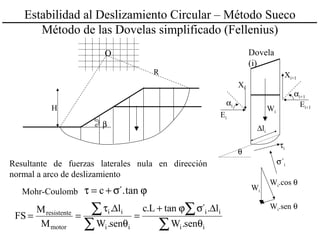
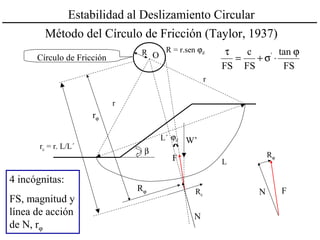
El documento describe diferentes métodos para analizar la estabilidad de taludes. Explica los tipos de taludes y fallas, y analiza la estabilidad frente a deslizamientos superficiales y circulares mediante el método sueco y el método del círculo de fricción. También menciona consideraciones generales como la elección de parámetros resistentes y el monitoreo de terraplenes de prueba.

1. ESTABILIDAD DE TALUDES
• Tipos de Taludes
• Tipos de Falla de Talud
• Cálculo de Estabilidad
• Estabilidad al Deslizamiento Superficial
• Estabilidad al Deslizamiento Circular
– Método Sueco
– Método del Círculo de Fricción. Ábacos de Taylor

2. Estabilidad de Taludes
Taludes:
– Suelo
– Roca
Taludes:
– Naturales
– Artificiales:
• Cortes
• Terraplenes

4. Estabilidad de Taludes
• Se debe determinar Factor de
seguridad al deslizamiento
• Factor de seguridad = 1 
Deslizamiento del talud
• Comparar colaboración de esfuerzos que tienden a producir
deslizamiento (esfuerzos motores) con los que tienden a evitarlo
(esfuerzos resistentes) Definir superficie de falla

5. Tipos de Fallas de Taludes
Varnes (1978)
(a) Caídas (“Falls”)
(b) Vuelco (“Topple”)
(c) Deslizamiento (“Slides”)
(d) Escurrimiento (“Spread”)
(e) Flujo (“Flow”)
• Deslizamientos:
• Superficiales
• Rotacionales
• Traslacionales

6. Deslizamientos Rotacionales
Falla Local
Falla de Pie
Falla Profunda o de Base
Material mas resistente
A partir de observaciones: En
general se toma superficie de falla
circular

7. Formación de Superficie de Falla
(Falla Progresiva)

8. Análisis de Estabilidad de Taludes
• Parámetros de Resistencia al Corte a ser usados:
• Arenas: φ
• Arcillas:
• Análisis a Corto Plazo (Final de Obra): Su
• Análisis a Largo Plazo: c; φ
• Situaciones en Arcillas:
• Terraplén sobre arcilla normalmente consolidada
• Excavación en arcilla sobreconsolidada

9. Análisis de Estabilidad de Taludes
Terraplén sobre arcilla normalmente consolidada

10. Análisis de Estabilidad de Taludes
Excavación en arcilla sobreconsolidada

11. • Superficie de falla plana y paralela a talud
• Masa que desliza de pequeño espesor
• Tensiones en caras verticales iguales y opuestas
Si se moviliza toda la resistencia al corte (FS = 1), talud será estable
para i = φ
i: ángulo de reposo
Estabilidad al Deslizamiento Superficial
ϕ=⇒
ϕ
=
⋅
ϕ⋅⋅
=
⋅
ϕ⋅
=
⋅⋅γ=⋅=⋅=
máx
d
i
inat
tan
FS
isenW
tanicosW
isenW
tanN
FS
daW;icosWN;isenWT
T
i
W
a
d
N
Equilibrio de fuerzas
Arena seca

12. Estabilidad al Deslizamiento Superficial
• Superficie de falla plana y paralela al talud
• Masa que desliza es de pequeño espesor
• No existe flujo de agua en el interior
T
i
W
a
d
N´
a.d.γw
Talud sumergido
ϕ=⇒
ϕ
=
⋅
ϕ⋅⋅
=
⋅
ϕ⋅
=
⋅⋅γ=⋅=⋅=
máx
'
'
'
'
'''''
i
inat
tan
FS
isenW
tanicosW
isenW
tanN
FS
daW;icosWN;isenWT
Arena sumergida

13. En general
• El talud es estable para i < ϕ
• El ángulo de fricción para el que comienza deslizamiento está
relacionado con ϕmáx (dependiendo de eo)
• Para arena suelta, ϕ = ϕcv.
Flujo de agua reduce estabilidad de talud
Estabilidad al Deslizamiento Superficial
itan
tan
FS
ϕ
=

14. O
Fuerzas Resistentes
W
G
R
Fuerzas Motoras
β
H
Su
d
Determinar centro
para menor FS
∑
∑==
ii
iui
motor
resistente
dW
lSR
M
M
FS
.
..
Suelo estratificado
dW
lRS
M
M
FS u
motor
resistente
.
..
==
Suelo uniforme
Estabilidad al Deslizamiento Circular – Método Sueco
Condición no drenada (Fellenius)

15. Estabilidad al Deslizamiento Circular – Método Sueco
Método de las Dovelas simplificado (Fellenius)
O
R
β
H
∑
∑
∑
∑
θ
∆σϕ+
=
θ
∆τ
==
ii
ii
ii
ii
motor
resistente
sen.W
l.´tanL.c
sen.W
l.
M
M
FS
ϕσ+=τ tan´.cMohr-Coulomb
Ei+1
Dovela
(i)
Wi
θ
Ei
∆li
σ´i
τi
Wi
Wi.sen θ
Wi.cos θ
Xi+1
Xi
αi
αi+1
Resultante de fuerzas laterales nula en dirección
normal a arco de deslizamiento

16. Estabilidad al Deslizamiento Circular
Método del Círculo de Fricción (Taylor, 1937)
O
W’
r
β
R
r
L´
L
R = r.sen ϕd
F
ϕd
Rc
rc = r. L/L´
Círculo de Fricción
N
Rϕ
rϕ
FS
tan
FS
c
FS
' ϕ
⋅σ+=
τ
N
Rϕ
F
4 incógnitas:
FS, magnitud y
línea de acción
de N, rϕ

17. Estabilidad al Deslizamiento Circular
Método del Círculo de Fricción (Taylor, 1937)
• Suponiendo rϕ = r quedan 3 incógnitas que pueden determinarse a
partir de las ecuaciones de equilibrio
• FS calculado a partir de esta hipótesis es un límite inferior
• Límite superior de FS se obtiene suponiendo esfuerzos efectivos
concentrados únicamente en los extremos del círculo de falla
(Frölich, 1955)
• En talud real esfuerzos normales estarán distribuidos sobre arco de
falla de forma desconocida
• Se tienen dos FS:
• Solución correcta es la que hace:
dce
c
tan
tan
FS;
R
Lc
C
C
FS
ϕ
ϕ
=
⋅
== ϕ
FSFSFSc == ϕ

18. • Solución particular de Método del Círculo de Fricción para círculo
de falla crítico en suelos homogéneos saturados (Taylor, 1948)
• Esfuerzos normales distribuidos de forma similar a semionda
sinusoidal
• Se define Coeficiente de Estabilidad (m):
• Para suelo homogéneo existen tres variables: m, ϕ y β
• Ábacos para determinación de círculos de falla críticos sin
necesidad de tanteos
• En suelos homogéneos con círculo crítico de base vertical
tangente a círculo de fricción pasa por punto medio de talud
Método del Círculo de Fricción
Ábacos de Taylor para Suelo Homogéneo Saturado (1948)
γ
=
.H.FS
c
m

19. • Existen métodos que consideran parcial o totalmente fuerzas entre
dovelas (Bishop, Jambu, Spencer)
• Existen métodos que suponen otros tipos de superficies de falla
(método de la cuña, espiral logarítmica, etc.)
• Método de dovelas simplificado da coeficientes de seguridad con
intervalo de confianza de ±10% respecto a parámetros de resistencia
supuestos. Fundamental elección de parámetros resistentes
• Otros casos a considerar: largo plazo con flujo en régimen
establecido (redes de flujo), vaciado rápido (elevadas presiones
neutras)
• Se puede ajustar parámetros de proyecto a partir de observación de
comportamiento de terraplenes de prueba instrumentados
(monitoreo de deformaciones y presiones neutras)
Consideraciones GeneralesConsideraciones Generales