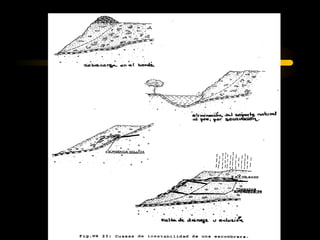
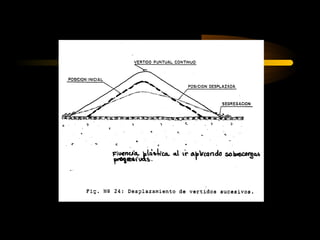
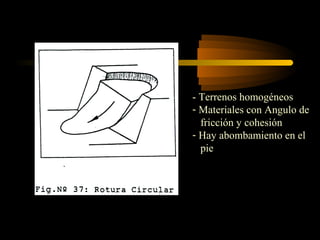
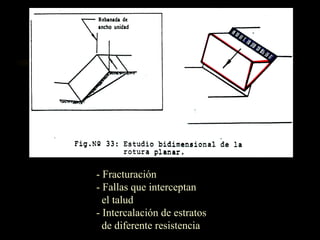
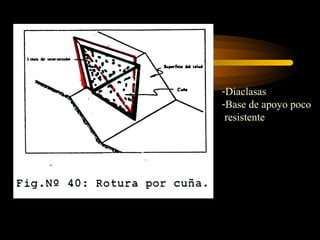
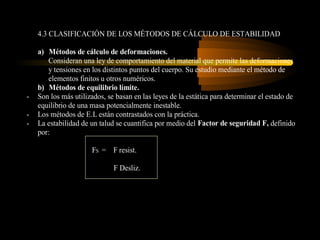
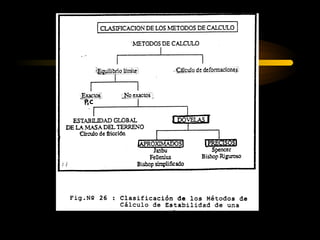
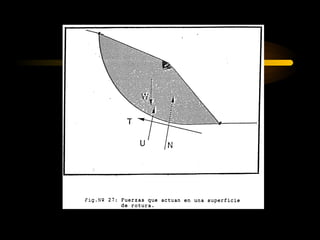
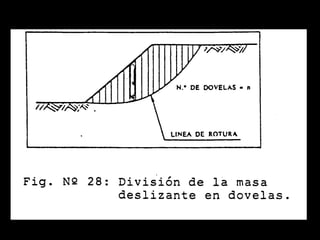
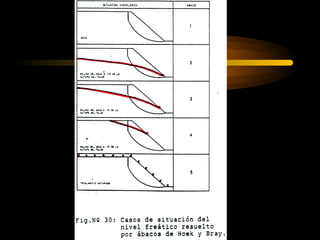
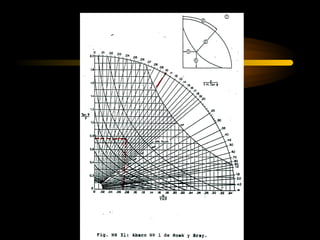
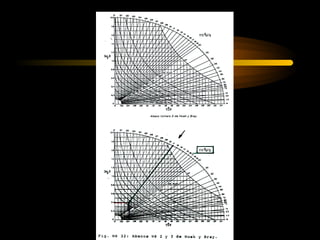
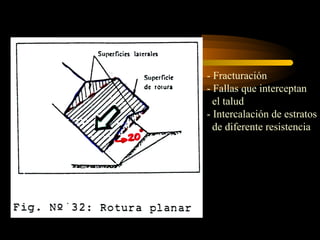
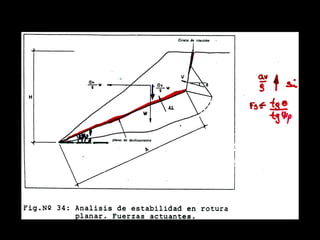
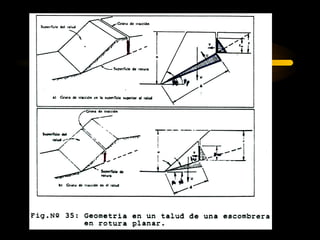
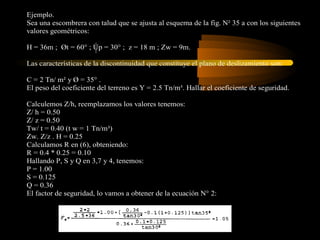
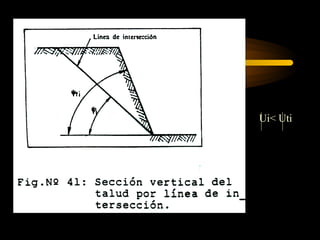
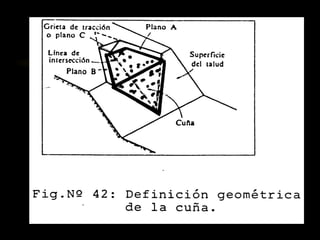
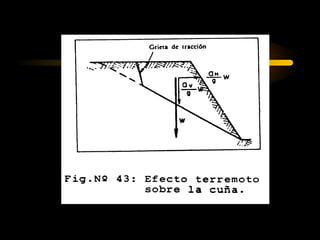
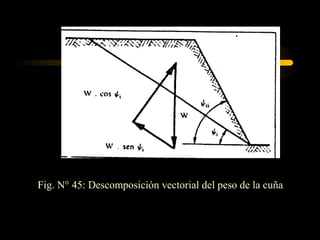
El documento describe diferentes métodos para analizar la estabilidad de taludes. Se mencionan cuatro formas comunes de inestabilidad y sus causas. Luego, se describen cuatro métodos para calcular el factor de seguridad de taludes: el método de Hoek y Bray para roturas circulares, el método para roturas planas, y los métodos de Spencer y Fellenius para analizar taludes divididos en franjas. Cada método utiliza ecuaciones basadas en la ley de Coulomb para determinar las fuerzas que mantienen el equilibrio.

1. ANÁLISIS DE ESTABILIDAD DE
TALUDES

2. 4.1 FORMAS DE INESTABILIDAD:
Los fenómenos de inestabilidad mpás frecuentes observados en escombreras corresponden
alos tipos siguientes:
- Deslizamientos superficiales, típicos de escombros sin cohesión. Rápidos y
bajos vólumenes.
- Deslizamientos profundos, de tipo aproximadamente circular o mixto, con tramos
paralelos a un contorno base. Materiales con rozamiento y cohesión. El movimiento
típico es un abombamiento al pie de los taludes.
Las causa de inestabilidad suelen ser:
• Sobrecargas
• Socavaciones
• Erosión interna.
• Presiones intersticiales por ascenso de nivel freático.
• Existen además fenómenos de fluencia plástica.

6. 4.2. FORMAS DE ROTURA:
Las formas de reales de superficie de rotura son diversas y depende de:
- La anisotropía del suelo
- La heterogeneidad de los materiales
- Las presiones intersticiales.
Entre las principales superficies de rotura tenemos:
a) Planas:
Cuando la estratigrafía presenta alternancias de capas muy diferentes, o cuando la
longitud de la línea de deslizamiento es muy grande en relación con el espesor de los
estratos.
b) Circular:
Se produce en depósitos en los que los materiales presentan una propiedades
geotécnicas homogéneas.
c) No Circular:
Es una superficie de rotura mixta que combina una sección circular y un deslizamiento.
Se presenta en materiales con características diferentes.
d) En Cuña:
Típica en los casos en que la base de apoyo no es lo suficiente resistente para soportar
el peso de los estériles

7. - Terrenos homogéneos
- Materiales con Angulo de
fricción y cohesión
- Hay abombamiento en el
pie

8. - Fracturación
- Fallas que interceptan
el talud
- Intercalación de estratos
de diferente resistencia

9. -Diaclasas
-Base de apoyo poco
resistente

10. 4.3 CLASIFICACIÓN DE LOS MÉTODOS DE CÁLCULO DE ESTABILIDAD
a) Métodos de cálculo de deformaciones.
Consideran una ley de comportamiento del material que permite las deformaciones
y tensiones en los distintos puntos del cuerpo. Su estudio mediante el método de
elementos finitos u otros numéricos.
b) Métodos de equilibrio límite.
- Son los más utilizados, se basan en las leyes de la estática para determinar el estado de
equilibrio de una masa potencialmente inestable.
- Los métodos de E.L están contrastados con la práctica.
- La estabilidad de un talud se cuantifica por medio del Factor de seguridad F, definido
por:
FS = F resist.
F Desliz.

11. - En la obtención del factor de seguridad se le supone constante en toda la superficie de
deslizamiento.
- Siguen la ley lineal de coulomb:
t = c + otgø
Donde:
T = Tensión tangencial máxima en un punto de la superficie de deslizamiento.
C = Cohesión de la superficie de deslizamiento.
O = Tensión normal a la superficie de deslizamiento en el punto considerado.
Ø = Angulo de rozamiento interno de la superficie de deslizamiento.
- Cuando la superficie de rotura no es conocida (caso más frecuente) se calculan los
factores de seguridad correspondientes a un cierto número de superficies y se define
como factor de seguridad de talud el mínimo obtenido.
- Trabajan con tensiones efectivas.
- Se seleccionan diversas superficies de rotura hasta llegar a la más critica para el talud
considerado, que será la que dé un menor coeficiente de seguridad.
- Estos métodos se clasifican en:
a) Método Exactos:
- Aplicados a roturas planas y curvas.

15. 4.4 DESCRIPCIÓN DE LOS MÉTODOS
4.4.1 MÉTODO DE HOEK Y BRAY.
- Es un método gráfico válido para superficies de rotura circulares.
- Los paso son:
a) Se elige el tipo de escenario que es probable que se presente sobre la estructura a
analizare.
b) Se calcula el valor adimensional:
C
Y*H*tagø
Donde:
T = densidad del material
H = altura del talud
C = cohesión aparente
Ø = ángulo de rozamiento interno.
c) En los ábacos se sigue el radio del valor encontrado anteriormente hasta que corte
a la curva que corresponde el ángulo del talud.
d) Se busca sobre los ejes vertical y horizontal los valores de tagø/FS Y Thfs, a partir
de los cuales se calcula el valor de FS, más conveniente.

16. Ejemplo.
Una escombrera de estériles de carbón con nivel freático que surge a ¼ de la altura del
talud. Los parámetros reintentes son: C = 40 KN/m2 , T = 18 KN/m3y ø = 22°.
Hallar el factor de seguridad para H = 50 m y un ángulo de talud de 25°.
C = 0.11
Y*H*tagø
Con el ábaco número 3 se obtiene los siguientes resultados:
Tgø = 0.4y C = 0.044
FS yHFS
El factor de seguridad del talud es 1.01.

20. 4.4.2. MÉTODO PARA ROTURA PLANAR.
- Para hablar propiamente de rotura planar, se deben cumplir dos condiciones:
a) Los rumbos o trazas horizontales del plano del talud y del plano de deslizamiento deben
ser paralelos, formando entre sí un ángulo máximo de 20°.
b) Los límites laterales de la masa deslizante ha de producir una resistencia al
deslizamiento despreciable.
- El factor de seguridad es:
Donde:
C = Cohesión efectiva en la superficie de deslizamiento.
Ø = Ángulo de rozamiento interno en la superficie de deslizamiento.
A = Área de la superficie de deslizamiento, de ancho unidad.
W = peso de la masa deslizante, de ancho unidad.
U = Ángulo que forma el plano de deslizamiento con la horizontal.
U = Resultante de las presiones intersticiales sobre el plano de deslizamiento.
8 = Ángulo que forma la grieta de tracción con la vertical.
V = Resultante de las presiones intersticiales sobre la grieta de tracción.
G = Aceleración de la gravedad.

21. - Fracturación
- Fallas que interceptan
el talud
- Intercalación de estratos
de diferente resistencia

22. La formula es aplicable al caso en que no se considera la ación del terremoto haciendo
a V = a H= 0 y al caso en que el terreno este seco totalmente U= V = 0.
Si realizamos las siguientes simplificaciones:
- El talud a estudiar es un plano de inclinación Ø. La superficie del terreno que queda
encima del talud es un plano horizontal.
- No se considera el efecto sísmico.
- La grieta de tracción es vertical.
- La distribución es triangular en las presiones intersticiales que actúan sobre la base de la
masa deslizante y sobre la grieta de tracción. El valor máximo se da en la intersección
entre las dos superficies.
Obtendremos las siguientes simplificaciones para la ecuación N² 1:
A= H–Z
SinUp

25. Donde:
H = Altura del talud.
Z = Profundidad al límite superior del talud.
Zw =Altura de agua en la grieta de tracción.
T = Peso especifíco de la masa deslizante.
Tw = Peso especifíco del agua
La ecuación (1) puede escribirse en función de los parámetros adimensionales de la forma
siguiente:

26. Donde:

27. Ejemplo.
Sea una escombrera con talud que se ajusta al esquema de la fig. N² 35 a con los siguientes
valores geométricos:
H = 36m ; Øt = 60° ; Up = 30° ; z = 18 m ; Zw = 9m.
Las características de la discontinuidad que constituye el plano de deslizamiento son:
C = 2 Tn/ m² y Ø = 35° .
El peso del coeficiente del terreno es Y = 2.5 Tn/m³. Hallar el coeficiente de seguridad.
Calculemos Z/h, reemplazamos los valores tenemos:
Z/ h = 0.50
Z/ z = 0.50
Tw/ t = 0.40 (t w = 1 Tn/m³)
Zw. Z/z . H = 0.25
Calculamos R en (6), obteniendo:
R = 0.4 * 0.25 = 0.10
Hallando P, S y Q en 3,7 y 4, tenemos:
P = 1.00
S = 0.125
Q = 0.36
El factor de seguridad, lo vamos a obtener de la ecuación N° 2:

28. Ui< Uti

32. Fig. N° 45: Descomposición vectorial del peso de la cuña

33. Fig. N° 46: Obtención de Na y Nb en una sección de la
cuña por un plano perpendicular a la línea de intersección

34. Si sumamos para todas las franjas, tendremos:
Donde:
Mi = cosai (1 + tanaitanØi)
Fs
- Esta ecuación es la que se usa para obtener el factor de seguridad.
- Como proceso Fs, aparece de modo implícito ha de obtenerse mediante un proceso
iterativo
- La simplificación asumida por Bishop hace que este método no cumpla el equilibrio de
las fuerzas horizontales y es estrictamente cierta si las fuerzas x fueran nulas o si se
cumple
Ø = Constante
A = constante.
Y estará tanto más alejada de la realidad cuanto mayor sea la variación de estos dos
ángulos.

35. b) Método de Spencer.
- La hipótesis de trabajo es que las fuerzas interfranjas están igualmente inclinadas
respecto a la horizontal Xi = 8Ei.
- Estableciendo el equilibrio de fuerzas horizontales, obtendremos:
Ti cosai – NiSenai= - ( Ei – Ei - 1)
Equilibrio de fuerzas verticales:
Ti senai + Nicosai = Wi – (Xi – Xi-1) = Wi – 8 (Ei – Ei-1)
Tomando momentos:
de la relación de Mohr – colomb:
Ti = Ci bi + (Ni - Uibi)tanØi
Fs

36. Resolviendo el sistema de 3n ecuaciones con 3n incógnitas, obtendremos un sistema de dos
ecuaciones implícitas en Fs y 8 de la forma:
Donde:

37. c) Método de Fellenius.
- La hipótesis es que la resultante de las fuerzas que actúan las caras de las rebanadas es
paralela a la base de las franjas:
- Tomando momentos con respecto al centro del circulo:
Estableciendo equilibrio de fuerzas según la dirección Ni, tenemos:
Ni = Wi cosai
De la expresión de Mohr y Coulomb, sumando para todas las franjas y sustituyendo los
valores de iNi, Ti, de las ecuaciones anteriores, se obtiene el coeficiente de
seguridad, el cual será igual a :