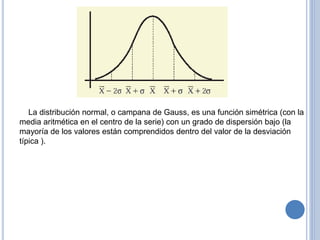
1) El documento describe diferentes medidas de tendencia central y dispersión para resumir distribuciones de frecuencias, incluyendo cuartiles, deciles, percentiles, rango, desviación media, varianza y desviación típica. 2) Estas medidas deben cumplir condiciones como depender de todos los valores y ser únicas, calculables y de fácil obtención para cada distribución. 3) Las medidas de dispersión indican qué tan dispersos están los valores con respecto al centro y proveen información adicional sobre la confiabilidad de las medidas de tend

1. Instituto Universitario Politécnico
“Santiago Mariño”
Extensión Barcelona
Escuela de ingeniería electrónica
Alumno:
Miguel Brunings
25.427.231
Febrero del 2017

2. Son indicadores usados para señalar que porcentaje de datos dentro de una
distribución de frecuencias superan estas expresiones, cuyo valor representa el
valor del dato que se encuentra en el centro de la distribución de frecuencia, por
lo que también se les llama " Medidas de Tendencia Central ".
Pero estas medidas de posición de una distribución de frecuencias han de
cumplir determinadas condiciones para que lean verdaderamente
representativas de la variable a la que resumen. Toda síntesis de una
distribución se considerara como operativa si intervienen en su determinación
todos y cada uno de los valores de la distribución, siendo única para cada
distribución de frecuencias y siendo siempre calculable y de fácil obtención.
Las medidas de posición nos facilitan información sobre la serie de datos que
estamos analizando. La descripción de un conjunto de datos, incluye como un
elemento de importancia la ubicación de éstos dentro de un contexto
de valores posible. Una vez definidos los conceptos básicos en el estudio de
una distribución de frecuencias de una variable, estudiaremos las distintas
formas de resumir dichas distribuciones mediante medidas de posición (o
de centralización), teniendo presente el error cometido en el resumen mediante
las correspondientes medidas de dispersión.

3. • Deben ser definidas rigurosamente y no ser susceptibles de diversas
interpretaciones.2.
• Deben depender de todas las observaciones de la serie, de lo contrario no
seria una característica dela distribución.3.
• No deben tener un carácter matemático demasiado abstracto.4.
• Deben ser susceptibles de cálculo algebraico, rápido y fácil.

4. 1. Cuartiles
Son medidas posicionales que dividen la distribución de frecuencia en cuatro
partes iguales. Se designa con el símbolo Qa.
Q1, Q2 y Q3 determinan los valores correspondientes al 25%, al 50% y al
75% de los datos.
Q2 coincide con la mediana.
Como se calculan los cuartiles:
1. Ordenamos los datos de menor a mayor
2. Buscamos el lugar que ocupa cada cuartil mediante la expresión:

5. Número impar de datos
2, 5, 3, 6, 7, 4, 9
Número par de datos
2, 5, 3, 4, 6, 7, 1, 9

6. Cálculo de los cuartiles para datos agrupados
En primer lugar buscamos la clase donde se encuentra
en la tabla de las frecuencias acumuladas.
Li es el límite inferior de la clase donde se encuentra la mediana.
N es la suma de las frecuencias absolutas.
Fi-1 es la frecuencia acumulada anterior a la clase mediana.
ai es la amplitud de la clase.

7. Ejercicio de cuartiles
Calcular los cuartiles de la distribución de la tabla:
Cálculo del primer cuartil

8. Cálculo del segundo cuartil
Cálculo del tercer cuartil

9. 2. Deciles
Son medidas de posición que dividen la distribución de frecuencia en diez
partes iguales y estas van de desde el numero uno hasta el numero nueve. Los
deciles se les designa con las letras Da.
Cálculo de los deciles
En primer lugar buscamos la clase donde se encuentra
en la tabla de las frecuencias acumuladas.
Li es el límite inferior de la clase donde se encuentra la mediana.
N es la suma de las frecuencias absolutas.
Fi-1 es la frecuencia acumulada anterior a la clase mediana.
ai es la amplitud de la clase.

10. Ejercicio de deciles
Calcular los deciles de la distribución de la tabla:
Cálculo del primer decil

11. Cálculo del segundo decil
Cálculo del tercer decil
Cálculo del cuarto decil

12. Cálculo del quinto decil
Cálculo del sexto decil
Cálculo del séptimo decil

13. Cálculo del octavo decil
Cálculo del noveno decil

14. 3. Percentiles
Un percentil es una de las llamadas medidas de posición no central
(cuartiles, deciles, quintiles, percentiles, etc) que se puede describir como una
forma de comparación de resultados, por ello es un concepto ampliamente
utilizado en campos como la estadística o el análisis de datos. El percentil es
un número de 0 a 100 que está muy relacionado con el porcentaje pero que no
es el porcentaje en sí. Para un conjunto de datos, el percentil para un valor
dado indica el porcentaje de datos que son igual o menores que dicho valor; en
otras palabras, nos dice dónde se posiciona una muestra respecto al total.
Cálculo de los percentiles
En primer lugar buscamos la clase donde se encuentra
en la tabla de las frecuencias acumuladas.

15. Li es el límite inferior de la clase donde se encuentra la mediana.
N es la suma de las frecuencias absolutas.
Fi-1 es la frecuencia acumulada anterior a la clase mediana.
ai es la amplitud de la clase.
Ejercicio de percentiles
Calcular el percentil 35 y 60 de la distribución de la tabla:

16. Percentil 35
Percentil 60

17. Representación grafica de los cuartiles
Representación grafica de los deciles

18. Las medidas de tendencia central ofrecen una idea aproximada del
comportamiento de una serie estadística. No obstante, no resultan suficientes
para expresar sus características: una misma media puede provenir de valores
cercanos a la misma o resultar de la confluencia de datos estadísticos
enormemente dispares. Para conocer en que grado las medidas de tendencia
central son representativas de la serie, se han de complementar con medidas de
dispersión como la varianza o la desviación típica.
La dispersión es importante porque:
• Proporciona información adicional que permite juzgar la confiabilidad de la
medida de tendencia central. Si los datos se encuentran ampliamente
dispersos, la posición central es menos representativa de los datos.
• Ya que existen problemas característicos para datos ampliamente dispersos,
debemos ser capaces de distinguir que presentan esa dispersión antes de
abordar esos problemas.
• Quizá se desee comparar las dispersiones de diferentes muestras. Si no se
desea tener una amplia dispersión de valores con respecto al centro de
distribución o esto presenta riesgos inaceptables, necesitamos tener habilidad
de reconocerlo y evitar escoger distribuciones que tengan las dispersiones más
grandes.

19. Concentración y dispersión
Las medidas de centralización ayudan a determinar el «centro de gravedad»
de una distribución estadística. Para describir el comportamiento general de la
serie se necesita, sin embargo, una información complementaria para saber si
los datos están dispersos o agrupados.
Así, las medidas de dispersión pueden definirse como los valores numéricos
cuyo objeto es analizar el grado de separación de los valores de una serie
estadística con respecto a las medidas de tendencia central consideradas.
Las medidas de dispersión son de dos tipos:
• Medidas de dispersión absoluta: como recorrido, desviación media,
varianza y desviación típica, que se usan en los análisis estadísticos
generales.
• Medidas de dispersión relativa: que determinan la dispersión de la
distribución estadística independientemente de las unidades en que se
exprese la variable. Se trata de parámetros más técnicos y utilizados en
estudios específicos, y entre ellas se encuentran los coeficientes de apertura,
el recorrido relativo, el coeficiente de variación (índice de dispersión de
Pearson) y el índice de dispersión mediana.

20. La distribución normal, o campana de Gauss, es una función simétrica (con la
media aritmética en el centro de la serie) con un grado de dispersión bajo (la
mayoría de los valores están comprendidos dentro del valor de la desviación
típica ).

21. Rango o recorrido
Es la medida de variabilidad más fácil de calcular. Para datos finitos o sin
agrupar, el rango se define como la diferencia entre el valor más alto (Xn ó
Xmax.) y el mas bajo (X1 ó Xmin) en un conjunto de datos.
Desviación media
Como medida de dispersión más frecuentemente utilizada, la desviación
media se define como la media aritmética de los valores absolutos de la
desviación de cada valor de la variable con respecto a la media. Su formulación
matemática es la siguiente:

22. Varianza y desviación típica
La desviación media no siempre suministra una idea clara del grado de
separación entre los valores de una variable estadística. Para estudios científicos,
se prefiere utilizar una pareja de parámetros relacionados que se conocen
como varianza y desviación típica.
La varianza se define como el cociente entre la suma de los cuadrados de las
desviaciones de los valores de la variable y el número de datos del estudio.
Matemáticamente, se expresa como:
Por su parte, la desviación típica, simbolizada por s, se define sencillamente
como la raíz cuadrada de la varianza:
Por lo tanto, se tiene que:
La varianza y la desviación típica, cada una con su respectivo valor, se usan
indistintamente en los estudios estadísticos.