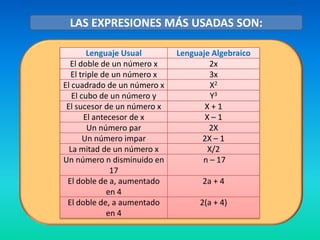
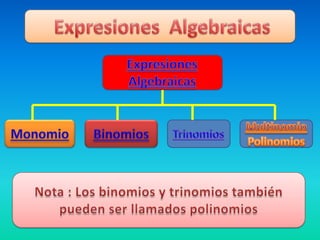
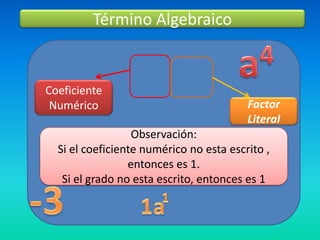
El documento explica cómo expresar problemas matemáticos que involucran números enteros, su doble, división y multiplicación usando el lenguaje algebraico. Específicamente, muestra cómo escribir un problema que involucra sumar un número a su doble, dividir el resultado por tres y multiplicarlo por dos usando letras en lugar de números. Luego, introduce conceptos como monomios, binomios, trinomios y polinomios, y cómo reducir términos semejantes en expresiones algebraicas.

2. El Lenguaje Algebraico
Si a un número entero le sumamos su doble, divides el resultado por 3 y,
finalmente, multiplicas todo por 2, ¿qué número obtienes?.
Para resolver problemas de este tipos recurrimos al Álgebra, es decir, a
la rama de la matemática que estudia la relación entre los números,
letras y signos.
Veamos cómo escribir este problema usando letras.
Sea a el número entero a
El numero entero más su doble a + 2a
Dividimos por tres a + 2a
3
Multiplicamos todo por 2 2 a + 2ª
3

3. LAS EXPRESIONES MÁS USADAS SON:
Lenguaje Usual Lenguaje Algebraico
El doble de un número x 2x
El triple de un número x 3x
El cuadrado de un número x X2
El cubo de un número y Y3
El sucesor de un número x X+1
El antecesor de x X–1
Un número par 2X
Un número impar 2X – 1
La mitad de un número x X/2
Un número n disminuido en n – 17
17
El doble de a, aumentado 2a + 4
en 4
El doble de, a aumentado 2(a + 4)
en 4

4. Ejercicios
1.- Expresa en lenguaje algebraico.
a) A aumentado en el doble de b. _______
b) Cincuenta menos el producto de diez por p. _______
c) La mitad de un número x, más su quina parte. _______
d) El cuadrado de un número y, disminuido en tres. _______
e) La diferencia de los cubos de x e y. _______
f) El sucesor de un número v. _______
g) Los 3 primeros múltiplos de x. _______
h) La suma de dos números es 8. _______
i) La diferencia de dos números es dos. _______
j) La suma de tres números es menor que diez. _______
2.- Si x es la edad Patricia, expresa en lenguaje algebraico
a) La edad de que tenía hace cinco años.
b) La edad que tendrá dentro de cinco años.
c) Los años que faltan para que cumpla 80

7. Monomio
Monomio es aquella Expresión Algebraica que posee solo
un Término algebraico
Ejemplos: -0,8xy
5 x2yz4
-25 q2 pz4

8. Binomio
binomio es aquella Expresión Algebraica que posee dos
Términos algebraicos
3yz 4 +7z
2 q2 + pz4
Ejemplos:
p+q
5 x2yz4 + 3xy
z 2x

9. Trinomio
Trinomio es aquella Expresión Algebraica que posee tres
Términos algebraicos
La practica
Ejemplos: hace al maestro
3xp + r- 6
z4 +7z + q
-2 q2 – x + pz4

10. Polinomio
Multinomio es aquella Expresión Algebraica que posee
cuatro o más términos algebraicos
Recuerda esto
Ejemplos: te acompañara
 x2 + 8x + xy + 5 siempre
 3a2b – 8 a2b – 7a2b + 3a2b
 d4 – d3 – d2 + d – 1 + 2

11. Término Algebraico
Coeficiente
Numérico Factor
Literal
Observación:
Si el coeficiente numérico no esta escrito ,
entonces es 1.
Si el grado no esta escrito, entonces es 1

12. Valor de una Expresión Algebraicas
Las expresiones algebraicas no representan valores en sí, sino que pueden
ser evaluadas para distintos valores que se les asignen a las letras que las
componen.
Ejemplos:
Sea x= 3 , y = -5 , reemplazando esos valores en la
expresión :
3xy + y- 5 =
3( 3 )( -5 )+(-5)- 5 =
9 (-5 ) - 5 - 5=
- 45 -10 = -55

13. Valor de una Expresión Algebraicas
Ejemplo:
Si a = 3 y b = 2, reemplazamos
esos valores en la expresión:
=3 a – 2b – 5a + 4b – 6a + 3b =
=3  3 - 2  2 - 5  3 + 4  2 - 6  3 + 3  2 =
= 9 - 4 - 15 + 8 - 18 + 6 = -14
Para x = 4
2x – 1 = 2.4 – 1 = 8 – 1 = 7
X² - 3 = 16 – 3 = 13
3x/2 = 3.4/2 = 12/2 = 6

14. Sucesiones
Ejemplo:
3, 7, 11, 15 … ¿Qué término sigue?
Si nos fijamos, cada término se
obtiene sumando 4 (+4) al anterior. Luego
el término siguiente será el número 19.
Pero si nos preguntan qué término ocupa
la posición 20, tendríamos que escribir
todos los números anteriores para saber
cuál es.
Esto se soluciona calculando la expresión
algebraica de su formación con respecto a
su posición o lugar que ocupa.

15. Sucesiones
Así:
3 , 7 , 11 , 15 , 19 , …
1 2 3 4 5
Como la serie va de 4 en 4, la regla en
cuanto a su posición será 4x, y para
obtener el valor exacto observamos que
debemos restar 1 (-1).
Luego la expresión quedaría como:
4x – 1
De esta forma el término veinte será:
4.20 -1 = 80 – 1 = 79

16. Sucesiones
Otro ejemplo:
5 , 8 , 11 , 14 , 17 , …
1 2 3 4 5
La serie va de 3 en 3 (sumar 3 al anterior
“+3”. Entonces, la regla de recurrencia será
3x, y para obtener el valor exacto
observamos que debemos sumar 2 “+2”.
Luego la expresión quedaría como:
3x + 2
De esta forma, p.e. el término doce será:
3.12 + 2 = 36 + 2 = 38

17. Sucesiones
Ejercicios:
1.- Calcula la regla de formación y el
término 15 de las siguientes sucesiones:
a) 1, 4, 7, 10, 13, …
b) 2, 4, 6, 8, 10, …
c) -7, -2, 3, 8, 13, …
d) 1, 4, 9, 16, 25, …
e) -2, 2, 6, 10, 14, ...
f) 2, 4, 8, 16, 32, …
g) 0, -2, -4, -6, -8, …
h) 3, 9, 15, 21, 27, …
i) 2, 5, 10, 17, 26, …
j) 1, 3, 5, 7, 9, …

18. Sucesiones
Solución:
a) 3x-2 T(15)= 3.15-2= 45-2= 43
b) 2x T(15)= 2.15= 30
c) 5x-12 T(15)= 5.15-12= 75-12= 63
d) x² T(15)= 15² = 225
e) 4x-6 T(15)= 4.15-6= 60-6= 54
f) 2ⁿ T(15)= 2¹⁵ = 32768
g) 2-2x T(15)= 2-2.15= 2-30= -28
h) 6x-3 T(15)= 6.15-3= 90-3= 87
i) x² +1 T(15)= 15² +1= 225+1= 226
j) 2x-1 T(15)= 2.15-1= 30-1= 29

19. Términos semejantes
Los términos son semejantes cuando tienen el mismo factor literal y el mismo
exponente es decir son idénticas.
Ejemplos:
En 2a2b-ab-3 a2b, los términos 2a2b y -3 a2b son semejantes.
En -0,2m3n-0,1mn2 -6 mn2 + m3n , hay dos pares de términos semejantes: -0,2m3n
con m3n y -0,1mn2 con -6 mn2
La expresión x3+ x2y+xy2+y3 no tiene términos semejantes.

20. Términos semejantes
Reducción de términos semejantes: se pueden reducir al sumar o restar, sumando o
restando sus coeficientes numéricos y conservando el factor literal.
La reducción se realiza bajo las siguientes reglas:
1.- si ambos son positivos, suma y se conserva el signo positivo
2.-si poseen signos diferentes, se restan y se conserva el signo del mayor valor
absoluto.
Ejemplo:
El término 3x2y y el término 2x2y, son semejantes. ( tiene factor literal iguales) y al
sumarlo da 5x2y
El término 6ab2+4ab-4 ab2-ab2+2 ab -11a-1 se reduce cada grupo de términos
semejantes
Reducir los términos con parte literal 6 ab2 -4ab2-ab2 = (6-4+1) ab2 =1 ab2= ab2
en los termino con parte literal ab: 4ab+2ab-11ab=(4+2-11)ab=-5ab
luego la expresión algebraica se reduce a: ab2-5ab-1

21. Ejercicios de reducción de términos
semejantes
Yo confío en
ustedes