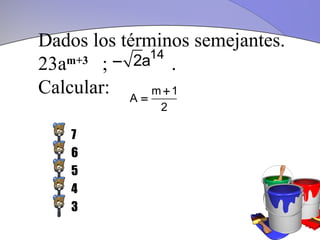
Este documento define expresiones algebraicas y proporciona ejemplos. Explica que una expresión algebraica relaciona valores indeterminados con constantes y operaciones. Describe cómo clasificar expresiones como racionales, irracionales, enteras o fraccionarias. Además, define términos como términos semejantes y coeficientes numéricos. Finalmente, explica cómo simplificar expresiones algebraicas mediante la suma de términos semejantes.

1. Expresiones
algebraicas

2. Objetivos de la lección
Definir e ilustrar ejemplos de términos
fundamentales relacionados con
expresiones algebraicas.
Explicar el proceso para simplificar
expresiones algebraicas.
Simplificar expresiones algebraicas
dadas.

3. Responde a las siguientes
interrogantes
¿De qué trata el video?
¿A qué se llama expresiones algebraicas?
¿Cómo se clasifican las expresiones
algebraicas?
¿Qué son términos semejantes

4. Definiciones
Fundamentales

5. Expresiones
algebraicas

6. Una expresión algebraica es
una expresión en la que se
relacionan valores indeterminados
con constantes y cifras, todas ellas
ligadas por un número finito de
operaciones de suma, resta,
producto, cociente, potencia y raíz.

7. Ejemplos de
Expresiones
Algebraicas
a ) x + 2 xy
2
b) 2 x + y x 2 3
x. y − 2 x
c) 2
x +1

8. Definiciones
V
Letra o símbolo que representa cualquier
cantidad o número. Se llama variable porque
esta cantidad puede variar.
Se refiere a un número. Se llama constante
porque su valor no varía, es siempre constante
el valor que represente el número.

9. Tipos de Expresiones Algebraicas
Expresiones Algebraicas
Racionales Irracionales
Enteras Fraccionarias

10. Expresión Algebraica Racional
Es racional cuando las variables no están
afectadas por la radicación
Ejemplo
x + x. y
2 2
+3
2 y +1
2

11. Expresión Algebraica Irracional
Es irracional cuando las variables están
afectadas por la radicación
Ejemplo
x +2x y

12. Expr. Algebraica Racional Entera
Una expresión algebraicas es racional entera
cuando la indeterminada está afectada sólo por
operaciones de suma, resta, multiplicación y
potencia natural
Ejemplo
x +3x y + y
2 4 5

13. Expr. Algebraica Racional
Fraccionaria
Una expresión algebraicas racional es
fraccionaria cuando la indeterminada aparece en
algún denominador.
Ejemplo
1 -1 2
+ x y −3
2
ó x + x y -3
x

14. Definiciones
1. Términos de una Expresión
SonAlgebraica –
aquellos que están separados por sumas o
restas
Son los términos que tienen –
2. Términos Semejantes las mismas
variables elevadas a las mismas potencias
Número que acompaña las variables
3. Coeficiente Numérico –
en un término

15. Definiciones
4. Grado de un término –
Es la suma de los exponentes de las variables
en un término
5. Grado de una expresión
algebraica –
Es equivalente al grado del término que tenga
el grado mayor. Para hallar el grado de la
expresión algebraica hay que hallar el grado
de cada término primero y luego ver cuál
es el grado mayor. Este será el grado de la
expresión.

16. ¿Habrán términos
¿Cuál es el grado de semejantes en cada
cada expresión expresión?
algebraica? 3x
¿Cuántos
términos
¿Cuáles son x4 - 10x + 11x tiene cada
los
expresión?
coeficientes
numéricos? 4x2y + 5xy2 + 5 x2y
-5x3yz - x2y2z2 + 4 - 2

17. Términos
1 término 3x
3 términos x4 - 10x + 11x
3 términos 4x2y + 5xy2 + 5 x2y
4 términos -5x3yz - x2y2z2 + 4 - 2

18. Términos semejantes
No hay 3x
-10x , 11x x4 - 10x + 11x
4x2y , 5 x2y 4x2y + 5xy2 + 5 x2y
4 , -2
-5x3yz - x2y2z2 + 4 - 2

19. Coeficientes numéricos
El signo que está
delante del número
3 3x le pertenece al
coeficiente
numérico.
1 , -10 , 11 x4 - 10x + 11x
4 ,5 ,5 4x2y + 5xy2 + 5 x2y
-5, -1, 4 , -2 -5x3yz - x2y2z2 + 4 - 2

20. Grado de expresión algebraica
Grado 1 3x
Grado 4 x4 - 10x + 11x
Grado 3 4x2y + 5xy2 + 5 x2y
Grado 6 -5x3yz - x2y2z2 + 4 - 2

21. Simplificación

22. Simplificación de
expresiones
algebraicas
1.
Pasos a seguir:
Localizar los términos semejantes.
2. Sumar solamente los coeficientes
numéricos de los términos semejantes
aplicando las reglas de suma de enteros.
(Recuerda que en la suma de enteros a
veces se suma y a veces se resta.)

23. Ejemplo 1: Simplifica
3x2 + 2x - 8 + 9 x3 + 6x – 7 – 4x2 =
3x2 + 2x - 8 + 9 x3
– 4x2 + 6x - 7
- x2 + 8x - 15 + 9 x3

24. Ejemplo 2: Simplifica
7 (2x2 + x - 8) =
Aplicar Propiedad Distributiva
14 x2 + 7 x - 56

25. Ejemplo 3: Simplifica
5x (x2 - 3x + 1) =
5 x3 - 15 x2 + 5x
Se suman los exponentes de las
variables

26. Ejemplo 4: Simplifica
5 (x – 2y) – (y - 3x) + (5x - 8y) =
5x – 10 y – y + 3x + 5x – 8y =
13 x - 19 y
El signo de – delante de un paréntesis es lo
mismo que si hubiera un –1. Se multiplica –1 por
cada término dentro del paréntesis cuando hay
un – delante de un paréntesis.

27. Practica
Simplificar
Expresiones
Algebraicas

28. Instrucciones
Simplifica cada expresión algebraica a
continuación.
Cuando hayas obtenido la respuesta, haz
clic en el botón correspondiente para ver
la respuesta.

29. 7x – 2x – 8 + x + 5x – 12 =
2 2
8x2 + 3x – 20
8x2 + 7x – 20
11x – 20
11x2 – 20
5x2 + 6x – 20

30. 5ab (a – 4ab + 2) =
5ab – 20 ab + 10 ab
5a2b – 20 a2b2 + 10 ab
35a2b2
-5a2b2
-5ab

31. - ( 2x - 3x + 6) =
2
- 2x2 – 3x + 6
- 2x2 – 3x - 6
- 2x2 + 3x - 6
2x2 – 3x + 6
2x2 + 3x - 6

32. 5 (x – 2y) – (y + 3x) + (5x – 8y) =
13x + y
13x3 + y3
13x – 19y
7x3 - 19 y3
7x – 19y

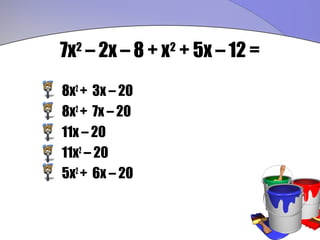
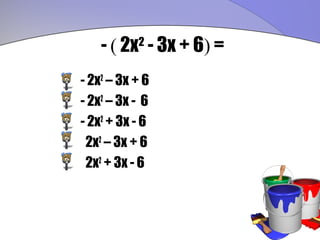
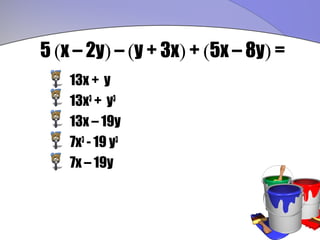
33. -2 { 3x + [x – (3x – 1)]}
-10x + 2
4x – 1
-8x – 1
-2x – 2
- 14x + 2

34. Si los términos t1 y t2
son semejantes.
t1 = 30x4 t2 = 4xa
Calcular: M = a +5
4
3
2
1
0

35. Dados los términos semejantes.
14
23am+3 ; − 2a .
Calcular: A = m + 1
2
7
6
5
4
3

36. Fin de la lección
Oprime aquí para salir