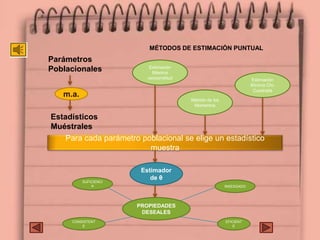
Este documento describe la familia exponencial y su utilidad para obtener estadísticos suficientes. La familia exponencial permite expresar la función de densidad de probabilidad de una muestra de forma que facilite el cálculo de un estadístico suficiente de dimensión k para el parámetro poblacional. Se proveen ejemplos como la distribución exponencial, Poisson, normal y beta. Pertenecer a la familia exponencial garantiza que el estadístico sea insesgado, eficiente y suficiente, incluyendo el caso de mín

1. “ Familia Exponencial”
Prof. Matías Hernández Sergio Alejandro
Integrantes:
Romero González Verónica
Ponce Rosas Diana Gisela Gpo.1502
Universidad Nacional Autónoma De México
Facultad de Estudios Superiores Acatlán
MAC

2. Índice
1. Objetivo
2. Introducción
3. Familia Exponencial
4. Ejemplos
5. Generalización para k-parámetros
6. Ejemplos
7. Conclusión
8. Bibliografía

3. Objetivo
Conocer la FAMILIA EXPONENCIAL ,
y su utilidad para obtener
estadísticos suficientes.

4. Introducción
IMPORTANCIA:
Si la distribución de Probabilidad de la muestra representada
por f( •, θ) admite la descomposición exponencial, esto
facilita el cálculo de un estadístico suficiente de dimensión k
para θ (parámetro poblacional)

5. mu
Tenemos muestra aleatoria x1,…,xn
f(•,θ) , tal que la función de
densidad se pueda expresar como:
Entonces dicha distribución pertenece
a la FAMILIA EXPONENCIAL y no es una
estadística suficiente.
De hecho, se puede demostrar que la
estadística suficiente para obtener es mínima.
muestra
θ=
?

6. Parámetros
Poblacionales
m.a.
Estadísticos
Muéstrales
Para cada parámetro poblacional se elige un estadístico
muestra
Estimación
Máxima
verosimilitud
Método de los
Momentos
Estimación
Mínima Chi-
Cuadrada
MÉTODOS DE ESTIMACIÓN PUNTUAL
Estimador
de θ
PROPIEDADES
DESEALES
INSESGADO
EFICIENT
E
CONSISTENT
E
SUFICIENCI
A

7. Familia Exponencial de Densidades
DEFINICIÓN. Una familia con un parámetro (θ es unidimensional)
de densidad f(*,θ) se puede expresar como:
Para y para una elección adecuada de las
funciones se definen concretamente a la
familia exponencial o clase exponencial.

8. Ejemplos
Si
entonces pertenece a la familia
exponencial para:
Distribución Exponencial
∴ pertenece a la clase exponencial

9. Distribución Poisson
Ejemplos
Si f(x, θ)= f(θ,λ) es la función de densidad de
una Poisson entonces :
Para
∴ pertenece a la clase exponencial

10. K-Parámetros de la Familia Exponencial
DEF. Una familia de densidad
puede ser expresada como:

11. K-Parámetros de la Familia Exponencial
Para una elección adecuada de las funciones
pertenece a la familia exponencial.
Observación: note que el número de
términos en la suma de exponentes es k y
por tanto la dimensión del parámetro.

12. Ejemplos
Distribución Normal
Si ,
donde
entonces
pertenece a la familia exponencial

13. Tome:
∴ pertenece a la clase exponencial

14. Distribución Beta
Tenemos la función de densidad de una distribución beta
Entonces se puede expresar
∴ pertenece a la clase exponencial
donde

15. Conclusiones
Una herramienta para encontrar los mejores
estimadores, es verificar que pertenecen a la CLASE
EXPONENCIAL
brinda:
Estimadores con CARACTERÍSTICAS DESEABLES.
 f(•,θ) de una m.a es MIEMBRO DE LA CLASE
EXPONENCIAL con k-parámetros entonces
d(x) es suficiente.
Condensa la info.
en la muestra sin
perder la info. de θ

16. ¿Por qué es una estadística suficiente
mínima?
Si pusiste atención…
Al pertenecer a la clase exponencial cumple con
ser insesgado, eficiente, y suficiente.
Donde tenemos 2 estimadores insesgados (T y T´)
y var (T)≤ var (T´) con mínima varianza entonces,
NO solamente tenemos un estimador insesgado
sino un UMVUE.(Estimador Uniformemente
insesgado de mínima varianza)

17. •Mood, Alexander McFarlane.
“Introduction to the theory of statistics”
Ed. McGraw – Hill. 1913
•Cepeda Cuervo, Edilberto.
“Estadística Matemática” Ed.
Universidad Nacional de Colombia
• Mateos, Gregoria. et. al. “Statistical
Methods”
Bibliografía