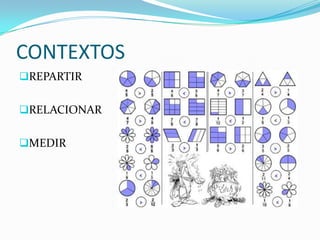
Este documento destaca la importancia de enseñar las fracciones y los números decimales como diferentes representaciones del mismo concepto subyacente de número racional. Propone evitar tratarlos como conceptos separados para ayudar a los estudiantes a comprender su relación. También enfatiza la necesidad de abordar este tema complejo con un enfoque que promueva la abstracción y la resolución de problemas en diferentes contextos.

1. “…Cuando en la escuela trabajamos con fracciones así como con números y
expresiones decimales, deberíamos tener en cuenta que estamos enfrentados a
recortes de transposición de un megaconcepto: número racional. Por lo tanto, lo
que intentamos es un acercamiento al concepto de número racional, concepto de
enorme complejidad y que requiere de un considerable nivel de abstracción. Sin
embargo, en ocasiones encontramos que tratamos números decimales y fracciones
como objeto de conocimiento distintos, impidiendo así que los alumnos logren
identificarlos como diferentes formas de representación del mismo número, lo que
no ayuda a la construcción del concepto.”
Liliana Pazos

2. SIGNIFICADOS DE LAS FRACCIONES
 RELACIÓN PARTE TODO.
OPERADOR
COCIENTE
EXPRESIÓN DE PROBABILIDAD

3. Aspectos a tener en cuenta en la
enseñanza.
 Relacionar en la recta numérica en forma periódica los
números naturales, con los decimales y los
fraccionarios.
 Abordaje de las fracciones por medio de
problematizaciones.
 Trabajar en forma intensa las propiedades de los
números decimales y procurar que el alumno
comprenda las diferencias con los números naturales.

4.  No limitar el trabajo con fracciones a la relación parte-
todo sino trabajar los otros sentidos de las fracciones y
abordarlas en los diferentes contextos.
 Analizar y explicar las distintas representaciones de un
mismo número (naturales, decimales, fracciones,
porcentajes).

5.  Usar diferentes estrategias de cálculo y de estimación
para resolver problemas en situaciones aditivas y
multiplicativas involucrando a números fraccionarios.
 Interpretar y producir información numérica muy
variada.

6. RELACIÓN PARTE - TODO
 A través de la relación parte todo se tiene un puente
de entrada a la conceptualización de la unidad como
un todo divisible en partes más pequeñas.

7. CONTEXTOS
REPARTIR
RELACIONAR
MEDIR

8. EJEMPLOS DE SITUACIONES CON
FRACCIONES
 COMO PARTE DE UN TODO.
Presentar al alumno varias figuras con secciones
pintadas en su interior. Preguntar qué parte de la
unidad representan.
 DE LA PARTE AL TODO
¿Cuánto le falta a 2/5 para obtener un entero?
¿Cuánto le falta a 2/5 para obtener dos unidades.

9. Como operador…
 De dos docenas de bombones, 2/3 son de dulce de
leche. ¿Cuántos bombones son de dulce de leche?
 Ya he colocado 132 libros en la biblioteca. Ellos son ¾
del total de libros a colocar. ¿Cuántos libros tendrá en
total la biblioteca?

10. Como cociente…
 Si quiero repartir dos pizzas entre tres amigos. ¿Cómo
puedo hacer?
COMO COMPARACIÓN…
 Sebastián y Marisa comen pizzas de igual tamaño.
Sebastián ha comido 2/3 de su pizza y Marisa 4/5 de la
suya. ¿Cuál de los dos ha comido más?

11. Como porcentaje…
 Para buscar el 35% de 420, dos niños realizaron
diferentes procedimientos:
JUAN MIGUEL
420 X 35/100 420 X 0,35.
Explica el procedimiento que realizó cada uno.

12. COMO PROBABILIDAD…
 Al tirar un dado ¿Cuál es la probabilidad de que saque
tres? Expresar en formato de fracción.
 En una clase hay 16 niñas y 8 varones. ¿Cuál es la
probabilidad de que salga el nombre de una niña?
Expresar el resultado en formato de fracción.

13. “ El alumno aprende adaptándose a un
medio que es factor de contradicciones, de
dificultades, de desequilibrios. Este saber,
fruto de la adaptación del alumno, se
manifiesta por las respuestas nuevas que
son la prueba del aprendizaje…”
BROUSSEAU

14.  TRABAJO REALIZADO POR JOSÉ MIGUEL DE
SOUZA
 DURAZNO - URUGUAY
 NOVIEMBRE DE 2012