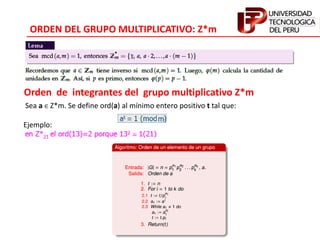
El documento trata sobre criptografía clásica y teoría de números. Explica conceptos como aritmética modular, congruencias, máximo común divisor, inversos módulo m, teorema de Euler, logaritmo discreto, residuos cuadráticos y raíces cuadradas módulo n. También presenta algoritmos como el de Euclides, el extendido de Euclides, exponenciación rápida y baby-step giant-step para calcular logaritmos discretos.

1. CRIPTOGRAFÍA CLÁSICA
Teoría de Números
Docente: Juan Carlos Broncano Torres
FISE-UTP Lima-Perú

2. Los Enteros Módulo n
La aritmética modular fue introducida en 1801 por Carl Friedrich
Gauss en su libro Disquisitiones Arithmeticae.
Algunas veces se le llama, sugerentemente, aritmética del reloj,
ya que los números «dan la vuelta» tras alcanzar cierto valor
llamado módulo.
Definición de congruencia
http://www.numbertheory.org/php/php.html

5. Clases residuales módulo m

7. Suma y producto en Zm
Así podemos ver que las demás operaciones
aritméticas modulares se definen como:

8. Si m es un número primo p, entonces todos los elementos de Zp salvo el cero tienen inverso.

9. Cualquier medio de transmisión es inseguro
Máximo común divisor

10. Algoritmo de Euclides
El algoritmo de Euclides se basa en la aplicación sucesiva del siguiente
lema:
Este resultado lo podemos usar para obtener un algoritmo para calcular
el máximo común divisor de dos números.

12. Algoritmo Extendido de Euclides.
El siguiente teorema establece la llamada “Identidad de Etienne Bezout”
aunque el resultado lo descubrió primero el francés Claude Gaspard
Bachet de Méziriac (1581-1638).

14. Inversos módulo m

17. Algoritmo para el cálculo del teorema chino de los restos congruentes

19. Existencia del inverso por Primalidad
Teorema fundamental de la aritmética
Nota: Observe que el número 1 no es ni primo ni compuesto. Esto garantiza la
unicidad de la factorización.

20. POTENCIAS mod m

22. Teorema de Euler
El teorema de Euler es uno de los grandes hitos en la desarrollo de
la teoría de números. Fue probado por Euler en 1760. Este teorema
extiende el teorema “pequeño” de Fermat a un módulo arbitrario.
Euler parece que no usaba una notación funcional para esta función;
él usó en algún momento la notación “πn”.
Gauss introdujo la notación “ ϕ(n)” aunque también se usa “Ø(n) ”. Sylverter introdujo la
notación “Totient (n)” que a veces aparece en la literatura actual.

23. Este teorema nos permite calcular ϕ(n) de manera directa, si conocemos la
factorización prima de n.
Ejemplo
ϕ(15) = ϕ(3∗5) = ϕ(3)* ϕ(5)=(3-1)(5-1) = 2∗4 = 8

24. Este teorema también puede formularse del siguiente modo:
Ejemplo
Este teorema parece algo extraño, ¿para qué usar fracciones si podemos calcular ϕ(n)
con enteros?.
Es cierto. Pero esta forma de expresar ϕ será de mucha utilidad más adelante cuando
aparezcan los factores (1 -1/pi) en productos infinitos.

25. De este Teorema podemos deducir como calcular el inverso multiplicativo en :
Cálculo de inversos con Teorema Euler

26. ¿Qué hacemos si no se conoce φ(n)?
Si no conocemos ϕ (n) o no queremos usar los teoremas de Euler o Fermat, siempre
podremos encontrar el inverso de a en el cuerpo n usando el Algoritmo Extendido de
Euclides.
Algoritmo Extendido de Euclides

27. Exponenciación Rápida
Ejemplo

29. ORDEN DEL GRUPO MULTIPLICATIVO: Z*m
Orden de integrantes del grupo multiplicativo Z*m
Sea a ∈ Z*m. Se define ord(a) al mínimo entero positivo t tal que:
Ejemplo:

30. Generadores de grupos Cíclico
G = { an | n ∈ Z }. Dado que un grupo generado por un elemento
de G es, en sí mismo
En teoría de grupos, un grupo cíclico es un grupo que puede
ser generado por un solo elemento; es decir, hay un
elemento a del grupo G (llamado "generador" de G), tal que
todo elemento de G puede ser expresado como una potencia
de a. En otras palabras, G es cíclico, con generador a, si
Grupo cíclico

31. Propiedades del grupo Cíclico Z*m

32. RAÍCES PRIMITIVAS Y LOGARITMO DISCRETO
Raíces Primitivas

35. Logaritmo discreto o Indicador

40. Algoritmo Shanks : Baby-step giant step

41. Algoritmo Baby-step giant step

43. RESIDUOS CUADRÁTICOS
Congruencias cuadráticas módulo m

45. Criterio de Euler

48. Símbolos de Legendre y Jacobi
El símbolo de Legendre nos permite establecer si un
número a es o no es residuo cuadrático módulo un primo
p, mediante un cálculo automático. La ley de la
reciprocidad cuadrática, una de las joyas de la teoría de
números, simplifica notablemente este cálculo.
El símbolo de Jacobi es una generalización del símbolo de
Legendre que permite una simplificación del cálculo
cuando el módulo no es primo.
Los estudios en residuos cuadráticos de Euler fueron
extendidos por Legendre. El símbolo de Legendre nos
proporciona una serie de reglas para el cálculo
automático. Estas reglas en el fondo, son aplicaciones
simplificadas del criterio de Euler.

49. En algunos textos se usa una definición alternativa: Si p es primo impar

50. Ley de Reciprocidad Cuadrática

52. Símbolo de Jacobi

53. Algoritmo SIJ((a; n)), que calcula el símbolo de Jacobi (a/n)

54. Raíces cuadradas modulares
Evidentemente, la raíz cuadrada de un valor entero módulo n existe, si y sólo si,
dicho valor entero es resto cuadrático módulo n. Además, en el caso de que exista, se
puede demostrar que dicha raíz cuadrada no es única. Existen diversos algoritmos
para el cálculo de raíces cuadradas módulo n. Para presentarlos, se distinguirán los
dos casos posibles que se pueden presentar: que el entero n sea un número primo o
bien que sea un número compuesto.
Raíz cuadrada módulo n, con n primo
En el caso de que n sea un número primo, se puede demostrar que todo valor
entero a, que sea resto cuadrático módulo n, tiene dos raíces cuadradas de la
forma r módulo n y tales que:
Existen algoritmos capaces de calcular estas raíces de forma eficiente, aunque
tienen una complejidad computacional bastante elevada. A continuación, se pasa a
explicar uno de ellos, debido a L.M. Adleman, Manders y G.L. Miller.

55. Se debe tener en cuenta que, n ≠2 y el valor entero a tiene que estar comprendido
entre 0 < a < n, siendo a resto cuadrático módulo n.
Algoritmo para el cálculo de raíces cuadradas módulo primo

58. Raíz cuadrada módulo n, con n compuesto
En este punto se describe el cálculo de raíces cuadradas módulo n, en el caso de que
n sea un número compuesto de la forma:
con p y q factores primos de n. En estas condiciones, se puede demostrar que todo
valor entero a, con 0 < a < n que sea resto cuadrático módulo n, tiene cuatro raíces
cuadradas módulo n. Estas, son de la forma ±x y ±y módulo n y tales que:
verificándose que:
En estas condiciones, las raíces ±x mod n se denominan no gemelas, al igual que
las raíces ±y mod n. Cualesquiera otras dos raíces se denominan gemelas. Las raíces
cuadradas de a módulo n pueden calcularse de forma eficiente si se suponen
conocidos los factores primos p y q de n.

59. Algoritmo para el cálculo de raíces cuadradas módulo compuesto