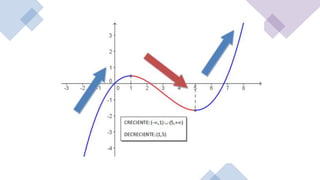
El documento aborda el estudio de funciones crecientes y decrecientes a través de la primera derivada, definiendo cómo determinar el comportamiento de una función en intervalos dados. Se explica que una función es creciente si su derivada es positiva y decreciente si es negativa, junto con aplicaciones en análisis de costos, demanda y optimización. Se presentan ejemplos y ejercicios para ilustrar estos conceptos en diversas áreas como economía y ingeniería.

1. Funciones
crecientes y
decrecientes,
aplicando la
primera
derivada

3. Introducción
En el estudio de las funciones, comprender el comportamiento de estas es fundamental.
Una de las herramientas más útiles para analizar el comportamiento de una función es su
primera derivada. En esta presentación, exploraremos cómo la primera derivada nos
permite determinar si una función es creciente o decreciente en un intervalo dado.

4. Definición de función creciente: Una función f(x) se dice que es creciente en un
intervalo I si para cualquier par de puntos x1 y x2 en I, con x1 < x2, se cumple que
f(x1) < f(x2).
Definición de función decreciente: Una función f(x) se dice que es decreciente
en un intervalo I si para cualquier par de puntos x1 y x2 en I, con x1 < x2, se
cumple que f(x1) > f(x2).
Concepto

5. Si la función f(x) es derivable en un intervalo I, entonces:
Si f'(x) > 0 para todo x
en I, entonces f(x) es
creciente en I.
Si f'(x) < 0 para todo x
en I, entonces f(x) es
decreciente en I.
Teorema de la primera
derivada

6. Aplicación
• Análisis de costos y beneficios: Determinar si el costo de
producción de un bien aumenta o disminuye a medida que
aumenta la cantidad producida.
• Análisis de la demanda: Estudiar cómo la demanda de un
producto cambia en función de su precio.
• Optimización: Encontrar el valor máximo o mínimo de
una función.
El análisis de funciones crecientes y
decrecientes tiene diversas aplicaciones en
áreas como la economía, la administración y
la ingeniería. Algunos ejemplos incluyen:

7. Ejemplos
Ejemplo 1: La función f(x) = x^2 es creciente
en el intervalo (0, ∞).
Solución: La derivada de f(x) es f'(x) = 2x. Para
x > 0, f'(x) > 0. Por lo tanto, f(x) es creciente
en (0, ∞).
Ejemplo 2: La función g(x) = -x^3 + 3x^2 - 2x +
1 es decreciente en el intervalo (1, 2).
Solución: La derivada de g(x) es g'(x) = -3(x -
1)(x - 2). Para 1 < x < 2, g'(x) < 0. Por lo tanto,
g(x) es decreciente en (1, 2).

8. Ejercicio 1: Determine si la función h(x) = x^3 - 2x^2 + x - 1 es creciente o
decreciente en el intervalo (-1, 1).
Ejercicio 2: Un fabricante de muebles estima que el costo total de producir x
unidades de un producto es C(x) = 0.005x^3 + 0.2x^2 + 10x + 500. ¿En qué
rango de producción el costo total es decreciente?
Ejercicios

9. Resumen
En esta presentación, hemos visto cómo la primera derivada nos permite determinar si
una función es creciente o decreciente en un intervalo dado. Esta herramienta es
fundamental para analizar el comportamiento de las funciones y tiene diversas
aplicaciones en áreas como la economía, la administración y la ingeniería.