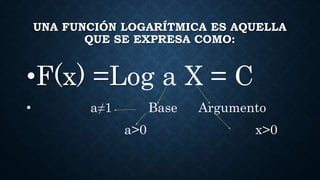
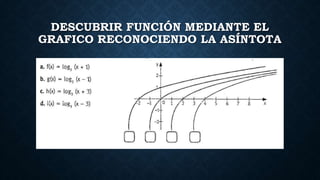
Las funciones logarítmicas son aquellas que se expresan como F(x) = Loga x, donde a es la base y x es el argumento. Estas funciones son inversas a las funciones exponenciales. Las funciones logarítmicas pueden ser crecientes si la base a es mayor que 1, o decrecientes si la base a está entre 0 y 1. Las funciones logarítmicas tienen una asíntota vertical en el eje y dada por el argumento.

1. FUNCION LOGARÍTMICA
Integrantes: Matias Fedre, Ramiro Córdoba, Augusto
Ibarguren y Nahuel Gimenez

2. UNA FUNCIÓN LOGARÍTMICA ES AQUELLA
QUE SE EXPRESA COMO:
•F(x) =Log a X = C
• a≠1 Base Argumento
a>0 x>0

3. PROPIEDADES DE LOS LOGARITMOS

4. FUNCIONES
LOGARITMICAS
LAS FUNCIONES LOGARÍTMICAS SON AQUELLAS
INVERSAS A LAS FUNCIONES EXPONENCIALES
• 1_Log a X = b ------ aˆb= X
• 2_si el argumento, en este caso “X” sea = a “1”, la
función se anula ya que : aˆ0=1
• 3_el eje Y es la asíntota vertical de la función. Y
esta se encuentra gracias al
argumento.(explicar)
• 4_Pueden ser crecientes ( a > 1)
• 5_pueden ser decrecientes (0<a<1)
PROPIEDADES
Ej:(log a X = b)

5. DESPLAZAMIENTO DE LA FUNCIÓN
Horizontal
• Depende del argumento
• Log a (X + 1)
• Se desplaza hacia abajo porque x+1 > 0
• Log a (X-1)
• Se desplaza hacia arriba porque x-1 > 0
Vertical
• Depende del termino que suma o resta al
Log
• Log a X + 1
• Se desplaza hacia arriba desde la
intersección eje x , ya que el termino es
positivo.
• Log a X -1
• Se desplaza hacia abajo ya que el termino
es negativo.

6. GRAFICAR UNA FUNCIÓN LOGARITMICA
Log 3 X Log 3 X+1

7. DESCUBRIR FUNCIÓN MEDIANTE EL
GRAFICO RECONOCIENDO LA ASÍNTOTA

8. REPASO: