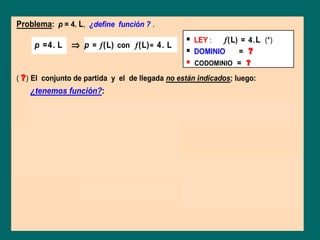
El documento define una función como una regla que asigna a cada elemento de un conjunto dominio un único elemento de un conjunto codominio. Explica que una función puede representarse como una máquina que toma valores de entrada y produce valores de salida basados en su mecanismo interno. También introduce conceptos como el dominio, codominio, gráfico de una función y cómo representar funciones gráficamente.

1. Funciones
por: Marta Bonacina
año: 2011

2. Definición de Función:
Dados dos conjuntos, A y B; llamamos función de A en B , a
“una regla o ley que a cada elemento de A asigna un único elemento de B ”
REGLA ó LEY
A B
1 1 4 8
3 9 2 π
2 5
16 2
3 49
16 π 2
4 25
25 7. 2

3. Una forma “moderna” de representar funciones es con los llamados:
"DIAGRAMAS DE MAQUINA"
x MÁQUINA f (x)
( TECLADO) ( CALCULADORA – PC ) (VISOR – PANTALLA)
f sería como una “procesadora” que :
 acepta x como “entrada”
 lo procesa según cierto “mecanismo” (la regla de f ),
 produce y = f (x) como “salida”.
La máquina, procesa los x´s a partir de distintos “mecanismos” , los que se
2
pueden representar por “ecuaciones”. Por ej, y = f (x )= x - 4x + 1. L ue go ,
♦ la x se “visualiza” como un “hueco a llenar al interior de la máquina” ; y,
♦ la regla o ley de f: como el “proceso” al que hay que someter a la x
cuando se “rellena” con ella, los huecos al interior de la máquina .
-2 -2
2
- 4 . + 1 13 f (- 2)

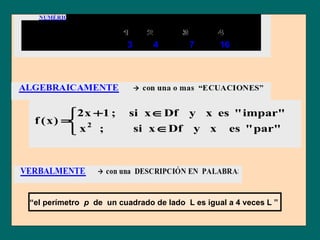
4. Definición de Función: Dados A y B; llamamos función de A en B , a
“una regla o ley que a cada elemento de A asigna un único elemento de B”.
En el ejemplo inicial, la función está presentada como una “máquina”.
¿Podremos “descubrir” la ecuación que gobierna el mecanismo de la misma?
REGLA ó LEY
A B
1 1 4 8
3 9 2 π
2
3 [ 2 + 1]2
1 16
9
4 5 2
16 π 2
4 25
25 7. 2
La ecuación es: y = ( x + 1)2
Que “leemos” : y = f ( x) con f ( x) = ( x + 1)2

5. f  función de A en B
f
A B
x Regla o Ley y

6. de llegada
CONVENCION DE NOMBRES y SIMBOLOS:
de partida A B
 f:A  B ; se lee : f aplica A en B . f
X y
y= f(x)
 al conjunto de partida ( A ), lo llamamos: DOMINIO
 al conjunto de llegada ( B ), lo llamamos: CODOMINIO
 a los elementos del dominio o del codominio los llamamos: VARIABLES.
Las variables las representamos con letras minúsculas: x, y, z, t , u, ….
 si y representa el valor obtenido de aplicar “f” a un x de A entonces:
lo llamamos Símbolo que usamos
   → imagen de x por f
 para enfatizar la
y función aplicada ( f ) y,
la variable elegida (x).
lo indicamos
     → y = f( x )

7. A B
f
X
y = f(x)
“ el valor de x en el dominio ,
se elige en forma arbitraria (entre los valores “posibles” para x ) ;
el correspondiente valor de y en el codominio ,
depende del valor de x previamente seleccionado ”

8. Existen otros conjuntos importantes asociados a función.
Uno de ellos: el conjunto “graf f ”. (gráfico de f )
Llamamos graf. f al conjunto de todos los pares ordenados
graf f cuya 1er componente es un elemento x del dominio (A) y,
su 2da componente, la imagen de x por f ; la indicamos:
f : A B
graf f = { (x ; y) / x ∈ A, y = f ( x ) }
graf f = { (x; f (x)) / x ∈ A }

9. Llamamos graf f al conjunto de todos los pares ordenados cuya
graf f primer componente es un elemento x del dominio y, su
segunda componente, la imagen de x por f ; lo indicamos:
f : A B
graf f = { (x; y) / x ∈A, y = f (x) }
Observación:
y C = graf f
Introducido un sistema de referencia
en el plano ( π ); se verifica que:
(x;y) P∈π
B
Esta correspondencia permite P
f(x)
representar gráficamente al conj. graf f .
eje horizontal ↔ Dominio (A) ↔ x
x x
eje vertical ↔ Codominio (B) ↔ y = f (x) A
{ P(x; y) / y = f (x); x ∈A } ↔ C: CURVA
PLANA

10. t
tt (hs) 32
OBSERVACIONES y EJEMPLOS: 32
32
30
 ¿Cuándo estamosLEY una función ? :
ante 28
28
tcada vez que tengamos una V(ls.)
(hs) 26
24
magnitud que “dependa” de otra. 24
24
0 8. [ ....] 0 22
V(ls)
20
8 [ ....]
Al abrir una canilla .para llenar un tanque, 20
2 4 18
el volumen de agua acumulado depende del tiempo. 16
8. [ ....] 8 16
8 16
16
 el volumen de agua acumulado es función del tiempo . 14
8. [ ....] 16
32 12
12
V(32)=
∆V = 12 16 ls
Si : V = volumen de agua en el tanque.
máquina
10
8
88
8
8
t = los objetivos de la matemática es
Uno detiempo transcurrido desde que 6
V(8) = 8 ls
hallar, se empieza a llenar elecuación” que
si existe, una “ tanque. 4 4
4
muestre como “opera” la “máquina” (LEY) V(2) = 4 ls
V= f (t) 22
sobre la “v.i.”, para obtener la “v.d.”
−18 −12−18 −6 −12 0 −6
6 12 0 18 6 24 1
−2
−4 −4
−6

11. t
tt (hs) 32
OBSERVACIONES y EJEMPLOS: 32
32
30
 ¿Cuándo estamos ante una función ? : 28
28
cada vez que tengamos una 26
24
magnitud que “dependa” de otra. 24
24
V(ls)
22
24 hs. 20
Al abrir una canilla para llenar un tanque, 20
18
el volumen de agua acumulado depende del tiempo. 16
16
16
16
 el volumen de agua acumulado es función del tiempo . 14
12
12 V(32)=
∆V = 12 16 ls
ΔV = 16 ls
Si : V = volumen de agua en el tanque. 10
8
88
8
8
t = tiempo transcurrido desde que 6
se empieza a llenar el tanque. 6 hs. ΔV = 4 ls
V(8) = 8 ls
4 4
4
V(2) = 4 ls
V= f (t) 2 hs.
2
2
−18 −12 −18 −6 −12 0 −6
6 12 0 18 6 24 1
−2
−4 −4
−6

12.  Con el tiempo el concepto de función evoluciona;
se usa tanto para representar relaciones de dependencia,
 del tipo causa-efecto, pertenecientes al mundo de lo concreto y real ;
 como relaciones de dependencia relativas al mundo de lo abstracto o ideal.

15. EJEMPLO 3
Las ecuaciones algebraicas con dos variables “abstractas” son ejemplos
típicos de relaciones de dependencia en el mundo de lo abstracto o ideal.
a) y = x +1
Por definición: y
 esta ecuación establece una relación entre dos variables abstractas.
En ella, a cada valor de x corresponde un único valor de y.
graf f ↔ { P(x; y) / y = f(x); x∈D }
Luego, considerando como dominio y codominio el conjunto R, la
graf f relación descripta = x + 1; ecuación, define función.
↔ { P(x; y) / y por esta x∈R }
La Geometría nos dice que:
dominio codominio
}↔
f : {R (x; y) / y = x +1; x∈R LEY RECTA
P R
x
x  y = x +1
Luego, y finalmente, tenemos que: x +1
y = f(x) con f(x) =
graf f ↔ RECTA
r = graf f

19. = ≠
= =
= =
≠
f = g g h

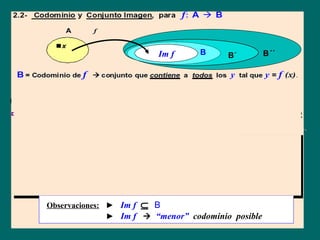
20. Ejemplo:
Analizar si “c” (costo) y “p” (perímetro) dadas a continuación son iguales:
(I) c = c(n) con c(n) = costo de ´n´ lápices de “costo unitario” $4.
(II) p = p(L) con p(L) = perímetro de un cuadrado de lado L.
1º) damos ley de cada función a través de una ecuación (facilita comparar)
(I) c = c(n) con c(n) = 4.n [ n: cantidad de lápices ]
( II ) p = p(L) con p(L)= 4.L [ L : longitud del lado del cuadrado ]
2º) damos el dominio natural de cada función.
(I) Dnc = N [ n ∈ N ; por ser una cantidad ]
( II ) Dnp = R + [ L ≥ 0 ; por ser una medida ]
0
3º) Conclusión : ley c = ley p ; Dnc ≠ Dn p
4º) Rta: las funciones costo y perímetro dadas no son iguales

21.  y= f(x)
Im f B B´ B´´
Observaciones: ► Im f ⊆ B
► Im f  “menor” codominio posible

22. NOTA:
en general a distintas leyes corresponden conjuntos imagen distintos;
pero; a leyes iguales pueden también corresponder imágenes distintas
( c: función “costo” ) (p: función “perímetro”)
 Ley : n → c = 4 n  Ley : L → p = 4 L
 Dominio = N  Dominio = R+
 Codominio = R  Codominio = R
 Im c = { 4; 8; 12; 16,…}  Im p = ( 0 ; +∞ )
c ≠ p

23. graf c = { P(n;c) / c = 4n ; n ∈ N } graf p = { Q(L;p) / p = 4L ; L∈ R+ }
24 24
20 20
16 16
12 12
graf p
8
graf c 8
4
4
1 2 3 4 5 6 7 8
1 2 3 4 5 6 7 8

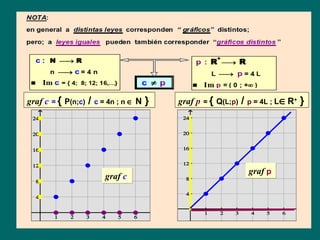
24. Las distintas formas de dar “la ley” de una función.
EJEMPLO 1:
► LEY: ECUACIÓN EN 2 VARIABLES
f : {[1 ; 3]}
1;2;3 → R  D = DOMINIO = { 1;2;3 }
[1 ; 3]
x → y = 2.x + 3 (* )  CODOMINIO = R
(*) se lee: y = f (x) con f (x) = 2.x + 3 ( imagen de x por f )
9
► LEY: TABLA DE VALORES 8
7
x 1 2 3 DOMINIO
6
y 5 7 9 IMAGEN
5
► LEY: GRÁFICO 4
graf f = { P (x;y) / x∈D; y = f (x) } 3
2
graf f graf f = { y) / x ;∈ [1; 3] ;(3;9) } + 3 }
= { P(x; (1;5) (2;7) ; y = 2x
1
−2 −1 1 2 3 4 5 6 7
−1

25. EJEMPLO 2: procedemos a analizar las siguientes expresiones coloquiales a los
efectos de decidir si las mismas ´definen función´ :
( I ) "el volumen de una esfera de metal (II) "el volumen de una esfera de metal
varia con el radio de la misma" varia con la temperatura de la misma"
(*) detectamos una relación de dependencia (*) detectamos una relación de dependencia
en que la correspondencia es unívoca en que la correspondencia es unívoca
⇓ ⇓
FUNCION FUNCION

26. ¿ Cómo expresamos estas funciones en "lenguaje matemático" ?
( I ) "el volumen de una esfera de metal ( II ) "el volumen de una esfera de metal
varia con el radio de la misma" varia con la temperatura de la misma"
1ro) reconocemos variables y elegimos letras apropiadas para identificarlas:
( I ) (radio)= r ; (volumen)= V ( II ) (temperatura)= t ; (volumen)= V
2do) establecemos el ´orden´ de dependencia:
( I ) el volumen depende del radio ( II ) el volumen depende de la temperatura
el volumen es función del radio. el volumen es función de la temperatura
V = f (r ) V=g(t)
3ro) explicitamos (de ser posible) la regla de correspondencia e indicamos Dn y Cn
( I ) V = f (r ) con f (r )= 4/3 π r 3 (II) V = g (t) con g (t )= ???
+
Dn = R
+
Cn =R
( * ) en este caso, acudiendo a la Geom. ; ( *) en este caso desconocemos una fórmula
podemos escribir la “ ley de f ” que relacione las variables; no podemos
a través de una fórmula. dar la “ley de g” con una “ecuación”
Esto plantea un problema: hallar la fórmula.

27. EJEMPLO 5
En un libro leemos: “el perímetro p de un cuadrado de lado L es; p = 4.L ”
 Esta conocida fórmula puede ser abordada desde dos perspectivas distintas:
 desde la Geometría: donde esto es una ecuación ; la cual india como
se calcula el perímetro conocido el lado;
y las letras tienen el carácter de dato ó incógnita
 desde el Cálculo: donde se reconoce como una relación de dependencia ,
o sea, como una expresión que muestra como el perímetro depende del lado
y en la que las letras tienen el carácter de variables.
Conclusión: la forma de interpretar y trabajar una fórmula depende del contexto en
el que se esté operando.
♦ Así, desde la óptica del Cálculo Matemático, la expresión leída en el libro la
registramos como una ´relación entre dos variables´.
Como a cada valor de L corresponde un único valor de p,
vemos que esta relación cumple con una de las condiciones de función.
Esta relación de dependencia. ¿ define función?

28. Problema: p = 4. L, ¿define función ? .
 LEY : f ( L) = 4. L (*)
p =4. L ⇒ p = f(L) con f(L) = 4. ⇒
L
 DOMINIO = ?
 CODOMINIO = ?
( ? ) El conjunto de partida y el de llegada no están indicados; luego:
¿tenemos función?:
Sí, estos conjuntos existen aún cuando no estén explícitamente Indicados.
La ley se ´aplica´ y ´produce´ números positivos.
Luego, p =4. L , define función:
f : R+ → R
+
L  → p = 4. L  LEY : f ( L) = 4. L (*)
+
 DOMINIO = R
f es función  CODOMINIO = R
+

30.  El(*) ¿ Quéde datos en forma gráfica posibilita
registro modelo ´ajusta mejor´ los datos ?. la búsqueda de una ecuación para f.
Según(*) curva (recta, parábola..) con la que aproximemos los “puntos soluciónpodemos obtener
la Se utilizó una de las curvas de ajuste para predecir la temperatura de la dato” a
distintas ecuaciones; luego, elegir entre ellas la que mejor “aproxima” a los “puntos dato”.
los 40´ . El resultado obtenido fue, 72,1 º C. ¿Qué modelo se usó?.
Por ej., las sgtes ecuacs resultan de aproximar,
(I) con una recta; (II) con una parábola
(I) Modelo lineal  τ =13,6 + 1.24 t (II) Modelo cuadrático  τ = 15,3 + 0.7 t + 0.018 t
2
(*) ¿ Qué modelo ´ajusta mejor´ los datos ?.
(*) Se utilizó una de las curvas de ajuste para predecir la temperatura de la solución a
los 40´ . El resultado obtenido fue, 72,1 º C. ¿Qué modelo se usó?.

31. EJEMPLO 4 la Física, muestra que, establecido un “sistema de referencia”
la altura y , en cada instante t , de un cuerpo arrojado hacia arriba,
se puede calcular según la siguiente ecuación:
y0 = altura inicial
1 2
y = yo + vo .t + a.t 9
v0 = velocidad inicial9
2
a = "g” acel. de la grav.
8
8
► Esta ecuación ¿define función ?: SI y
7 y graf f
y = f (t) con f (t) = yo + vo t + 1 at
2 ymax
2
6
► Analizamos un caso particular: 5
y0 = 0 ; v0 = 5 ; a = - 2  y = 5 t - t2 y
4
Trayectoria  3
Luego: y = f (t) No permite ver
el instante “ t” 2
Dn f = ¿??? 5 ]
[ 0; en que tiene la
altura “y” 1
+
Cod f = ¿??? t
Ro
−2 −1
−2 −1 1 2 3
2 2,5 3 4
4 5
5 6
6 7
Img f = [ 0; 6.25 ]
¿??? −1
−2

32. ¿ Existirá alguna función que describa la altura
de este cuerpo, “ para todo t ≥ 0” ?.
Si , tal función existe; lo que no es posible es
describir dicha altura con “una” ecuación. Así:
 cuando el cuerpo está cayendo, la altura del mismo respecto
del piso se expresa a través de la correspondiente fórmula física,
 cuando el cuerpo queda en “reposo” debemos acudir a otra ecuación:
y = 0.
El hecho que la ley de la función esté constituida por
más de una fórmula, lo indicamos como sigue:
y
2
5t - t ; 0≤ t ≤ 5 t=5
f (t) =
0 ; t > 5
 Las funciones definidas por varias leyes, como la del ejemplo,
reciben el nombre de funciones seccionalmente definidas .

33. RESUMEN
 DISTINTAS FORMAS DE ´DAR´ LA LEY DE UNA FUNCIÓN.
I - ALGEBRAICAMENTE  con una (ej. 2 dos (ej. 10 ) ó más ecuaciones.
Ej. 2),
II- NUMÉRICAMENTE  con una TABLA de VALORES (ej.1: τ = f ( t ) )
III - GRÁFICAMENTE  con una gráfica (ej. 9: τ = f ( t ) )
IV- VERBALMENTE  con una descripción en palabras (ej. 5 )

34. Definición de FUNCIÓN: Dados A y B; llamamos función de A en B , a
“una regla o ley que a cada elemento de A
asigna un único elemento de B”.
A B
1 1 33 8 2
2 3 9 2 π
45 2
2
3
15 7
7 8π
Regla o Ley
4 3,4
que puedo dar como 16
3 4 7 16

35. 3 4 7 16
y
18
16
14
12
10
8
6
4
2
x
−1 1 2 3 4 5 6

36. 3 4 7 16
 2 x +1 ; si x ∈Df y x es " impar"
f ( x) = 2
x ; si x ∈Df y x es " par"
“el perímetro p de un cuadrado de lado L es igual a 4 veces L ”