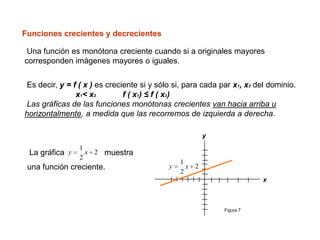
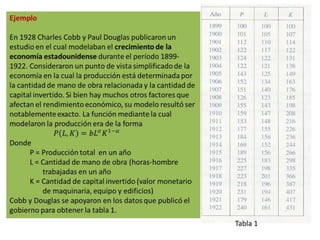
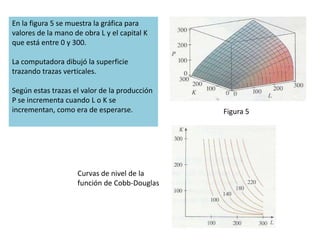
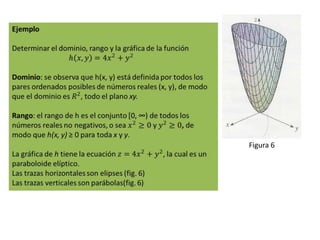
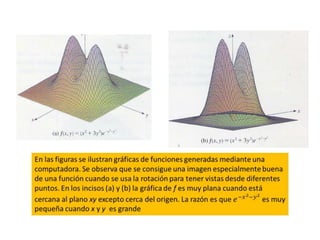
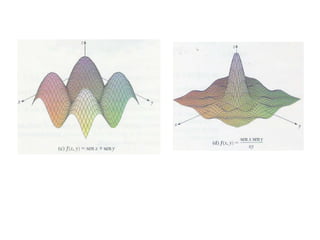
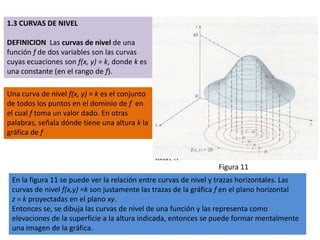
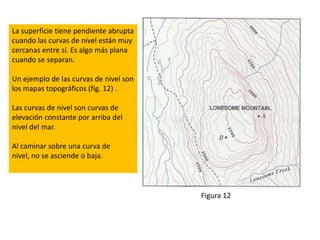
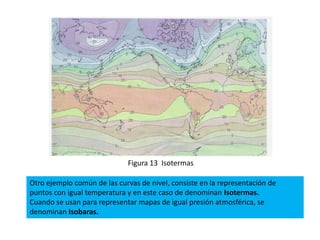
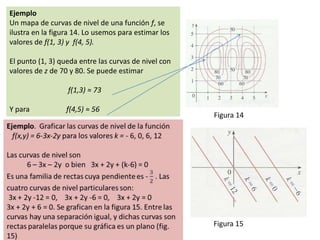
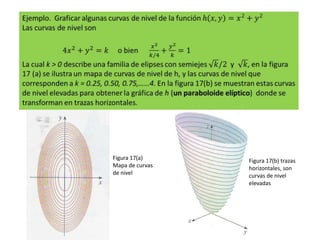
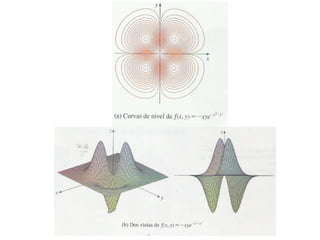
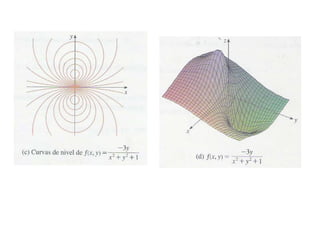
Este documento presenta conceptos básicos sobre funciones escalares de varias variables. Define una función como un conjunto de pares ordenados donde cada valor de x determina un valor único de y. Explica cómo representar funciones verbalmente, numéricamente, visualmente y algebraicamente. También cubre el dominio y rango de funciones, y cómo graficar funciones de dos o más variables.

1. UNIDAD 1 FUNCIONES ESCALARES DE VARIAS VARIABLES
Objetivo. En este capítulo se prepara el camino para el cálculo al
analizar las ideas básicas referentes a las funciones, sus gráficas y las
maneras para transformarlas y combinarlas.
1.1 Definición de función
Definición 1. Una función es un conjunto de pares ordenados con la
propiedad de que todo valor x únicamente determina un valor y. (es
importante mencionar que una función es una relación, pero una relación
puede que no sea una función).
Definición 2. Una función f es una regla que asigna a cada elemento x de
un conjunto D exactamente un elemento, llamado f(x), de un conjunto E.

2. 1) El crecimiento de la población P, de una ciudad, depende del tiempo t .
2) El costo C al enviar por mensajería documentos, o sea, que el costo
depende del peso de los documentos.
3) La velocidad de caída de un cuerpo depende de la altura a la que se deja
caer.
4) El gasto Q de agua que escurre en el cause de un río, es función de la
profundidad h del cauce o de la velocidad del agua, o sea, a mayor
profundidad mayor será el gasto Q, o bien, a mayor velocidad el gasto
Q aumenta. Q = f(h, v)

3. 1.1.1 Formas de representar las funciones
•Verbalmente (mediante una descripción en palabras)
• Numéricamente (con una tabla de valores)
• Visualmente (mediante una gráfica)
•Algebraicamente (por medio de una fórmula explícita)
Ejemplo. El crecimiento poblacional es función del tiempo y se puede
describir usando los cuatro pasos indicados.
1) se ha descrito verbalmente la función: la población P(t) de una ciudad
cambia con respecto al tiempo t.
2) La tabla representa numéricamente a la función que determina el
cambio de población P con respecto al tiempo t

4. 2) Representación de una función mediante una tabla de valores
Año Población Año Población
(en miles) (en miles)
1900 10000 1960 65870
1910 15200 1970 83400
1920 22300 1980 100390
1930 30800 1990 120500
1940 39550 2000 143780
1950 50900
3) Definición algebraica de la función de población de una ciudad.
Para 1900 < t ≤ 1940
Para 1940 < t ≤ 2000 P(t) = mt + b

5. 4) Representación del crecimiento poblacional mediante una gráfica.
Población ( P)
200 000
P(t) = mt + b
150 000
100 000
P(t) = kx2
50 000
1900 1910 1920 1930 1940 1950 1960 1970 1980 1990 2000 Tiempo ( t)
Figura 1

6. Ejemplo 2
Un recipiente rectangular para almacenamiento, con su parte superior
abierta, tiene un volumen de 15 m3 . La longitud de su base es el
doble de su ancho. El material de la base cuesta $550/m2 y el
material para los lados, cuesta $350/m2 . Expresar el costo del
material como función del ancho de la base.
Solución.
Es conveniente dibujar un diagrama como el de la figura 2 e introduciendo
la notación w y 2w como el ancho y la longitud de la base,
respectivamente, y h como la altura.
h
w
2w

7. Área de la base A (2w)( w) 2w 2 Para expresar C como función sólo
de w, se necesita eliminar h, lo que
de modo que el costo de la base es
sucede al aplicar el hecho de que el
500 (2w 2 ) volumen es de 15 m3 . De este
Dos lados del depósito tiene un área modo,
A =wh w(2w)h = 15
Y los otros dos tienen de donde resulta
15 7.5
A = 2wh h (2)
2w 2 w2
Entonces el costo para las cuatro Si se sustituye (1) en (2) para
paredes es encontrar C
350[2(wh) + 2(2wh)] . 7.5 15750
C 1000 w 2 2100 w 1000 w 2
w2 w
En consecuencia el costo total es
C = 500(2w2) + 350[2(wh) + 2(2wh)] (1) Por lo tanto, la ecuación
180
C ( w) 1000w 2 donde w 0
w
Queda expresado C como función de w

8. 1.2 Dominio y rango de funciones de varias variables
Para el cálculo del dominio de una función dada por su fórmula, debemos de
tener en cuenta que:
1) No es posible la división por 0.
2) No es posible extraer raíces cuadradas, raíces cuartas, sextas.
etc., cuando el radicando es negativo (si es posible la raíz de índice
impar).
3) No es posible calcular el logaritmo de un número negativo, ni tampoco
de 0.

9. 1
Ejemplo. Hallar el dominio de la función y f ( x)
x2 4
f(x) será un número real si x2 4 no es cero. Resolviendo la ecuación
x2 4 0 implica que x2 4 así que x 2 4 son los valores
que anulan al denominador. Por lo tanto el dominio es D = R - { -2, 2}
Ejemplo. Hallar el dominio de la función g ( x) 3x 9
La función está definida sólo cuando 3x + 9 es mayor o igual que cero.
Resolviendo 3x + 9 ≥ 0 implica 3x ≥ - 9 x ≥ - 3 de donde deducimos
que el dominio D = ( -3, ∞ ).
Ejemplo. Hallar el domino de la función h( x) x 1 1 x
Solución h (x) está definida para aquellos x ε R que hagan los dos
radicandos no negativos:
x–1≥0 y 1–x≥0 x≥1 y x≤1 x=1
Por lo tanto el dominio de la función está formado únicamente por D = {1}.

10. 1.2.1 Gráfica de funciones de varias variables
A la vista de la gráfica de una función, el dominio está formado por los
puntos del eje x o encima o debajo de los cuales hay gráfica.
Ejemplo. para la función cuya gráfica es la siguiente
y
El dominio es
D = ( - ∞, - 3) U [ (-1,0) U (0, 1) U (1, ∞) ]
-3 -1
x
1
Figura 6

11. Funciones crecientes y decrecientes
Una función es monótona creciente cuando si a originales mayores
corresponden imágenes mayores o iguales.
Es decir, y = f ( x ) es creciente si y sólo si, para cada par x1, x2 del dominio.
x1< x2 f ( x1) ≤ f ( x2)
Las gráficas de las funciones monótonas crecientes van hacia arriba u
horizontalmente, a medida que las recorremos de izquierda a derecha.
y
1
La gráfica y x 2 muestra
2
1
una función creciente. y x 2
2
x
Figura 7

12. FUNCIONES DE DOS O MAS VARIABLES
DEFINICION Si f es una función de
dos variables con dominio
D, entonces la gráfica de f es el
conjunto de todos los puntos (x, y, z)
en R³ tal que z = f(x, y, z) y (x, y) está
en D
La gráfica de una función f de dos
variables es una superficie S cuya
Figura 1. Gráfica de una ecuación es z = f(x, y).
función. Puede representarse la gráfica S de f
directamente encima o debajo de su
dominio D en el plano xy como se
indica en la figura 1.

13. Ejemplo.
Graficar la función f(x,y) = 6 – 3x – 2y
La gráfica tiene la ecuación: z = 6 – 3x – 2y o
3x + 2y + z = 6 que representa una plano
Para graficar el plano, primero se calculan las
intersecciones con los ejes.
- Al hacer y = z = 0 en la ecuación se obtiene x =
2 como intersección en el eje x
Figura 2
- Con el mismo procedimiento se obtiene la
intersección con el eje y que es 3 y la del eje
z, que es 6
- Con estos datos se puede graficar la parte de la
gráfica que está en el primer octante, ver la
figura 2

14. Figura 3. Gráfica del dominio de la función
Figura 4 Gráfica de la función

15. Tabla 1

16. En la figura 5 se muestra la gráfica para
valores de la mano de obra L y el capital K
que está entre 0 y 300.
La computadora dibujó la superficie
trazando trazas verticales.
Según estas trazas el valor de la producción
P se incrementa cuando L o K se
incrementan, como era de esperarse. Figura 5
Curvas de nivel de la
función de Cobb-Douglas

18. Figura 6

21. 1.3 CURVAS DE NIVEL
DEFINICION Las curvas de nivel de una
función f de dos variables son las curvas
cuyas ecuaciones son f(x, y) = k, donde k es
una constante (en el rango de f).
Una curva de nivel f(x, y) = k es el conjunto
de todos los puntos en el dominio de f en
el cual f toma un valor dado. En otras
palabras, señala dónde tiene una altura k la
gráfica de f
Figura 11
En la figura 11 se puede ver la relación entre curvas de nivel y trazas horizontales. Las
curvas de nivel f(x,y) =k son justamente las trazas de la gráfica f en el plano horizontal
z = k proyectadas en el plano xy.
Entonces se, se dibuja las curvas de nivel de una función y las representa como
elevaciones de la superficie a la altura indicada, entonces se puede formar mentalmente
una imagen de la gráfica.

22. La superficie tiene pendiente abrupta
cuando las curvas de nivel están muy
cercanas entre sí. Es algo más plana
cuando se separan.
Un ejemplo de las curvas de nivel son
los mapas topográficos (fig. 12) .
Las curvas de nivel son curvas de
elevación constante por arriba del
nivel del mar.
Al caminar sobre una curva de
nivel, no se asciende o baja.
Figura 12

23. Figura 13 Isotermas
Otro ejemplo común de las curvas de nivel, consiste en la representación de
puntos con igual temperatura y en este caso de denominan Isotermas.
Cuando se usan para representar mapas de igual presión atmosférica, se
denominan Isobaras.

24. Ejemplo
Un mapa de curvas de nivel de una función f, se
ilustra en la figura 14. Lo usemos para estimar los
valores de f(1, 3) y f(4, 5).
El punto (1, 3) queda entre las curvas de nivel con
valores de z de 70 y 80. Se puede estimar
f(1,3) ≈ 73
Y para f(4,5) ≈ 56
Figura 14
Figura 15

25. Figura 16

26. Figura 17(a) Figura 17(b) trazas
Mapa de curvas horizontales, son
de nivel curvas de nivel
elevadas