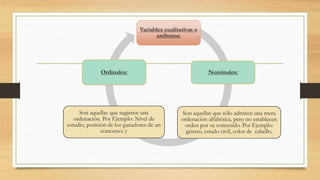
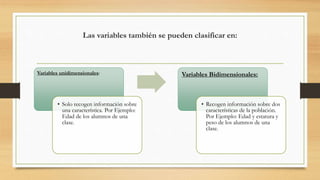
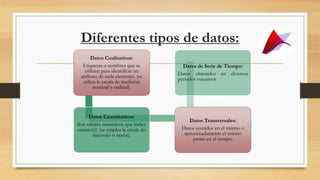
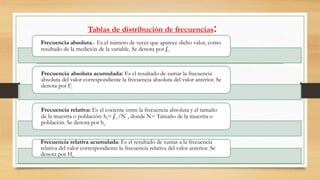
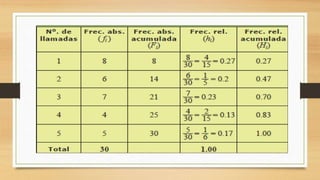
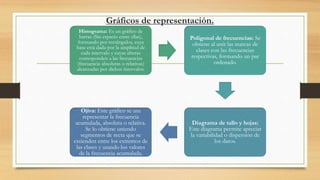
Este documento presenta una introducción general a la estadística. Explica que la estadística surgió para recopilar y describir datos sobre estados y países. Luego describe las tres etapas históricas de la estadística y ofrece definiciones de la estadística. También resume los objetivos, importancia, relación con otras disciplinas, división en estadística descriptiva e inferencial, tipos de variables y datos, y formas de presentar datos como tablas y gráficos. El documento concluye que la estadí

1. GRUPO N° 1
INTRODUCCIÓN A LA
ESTADISTICA

2. Introducción a la Estadística.
Primera etapa (Los
censos)
Segunda Etapa (De
la descripción de
los conjuntos a la
aritmética política)
Tercera etapa
(cálculo de
probabilidades)
El término estadística se deriva de la palabra latina status (que significa “estado”). Los
primeros usos de la estadística implicaron la recopilación de datos y la elaboración de
gráficas, para describir diversos aspectos de un estado o de un país.

3. Significados
Ciencia que recoge, organiza, presenta, analiza e interpreta datos
con el fin de propiciar la toma de decisiones más eficaz.
La estadística es la ciencia cuyo objetivo es reunir información
cuantitativa concerniente a individuos, grupos, series de hechos, etc.
para deducir de su análisis, conclusiones precisas o previsiones para el
futuro.
Ciencia inductiva que permite inferir características cualitativas y
cuantitativas de un conjunto mediante los datos contenidos en un
subconjunto del mismo

4. Objetivo
• El objetivo fundamental de la estadística es analizar datos y transformarlos
en información útil para la tomar decisiones.

5. Importancia de la estadística
• Los hombres y mujeres de negocios, en su eterna búsqueda de la
rentabilidad, consideran que la estadística es esencial en el proceso de toma
de decisiones.
• Para quienes están en el área de la investigación de mercados, la estadística es
de gran ayuda en el momento de determinar qué tan probable es que un
producto nuevo sea exitoso

6. Su relación con otras asignaturas.
• La investigación en Psicología, Sociología y Educación, al igual que ocurre en
otras ciencias, en buena medida se basa en el manejo de recursos estadísticos
como elementos esenciales para llegar a conclusiones aceptables por el resto
de la comunidad científica.

7. • La física estadística o mecánica estadística es la parte de la física que
trata de determinar el proceder agregado termodinámico de estructura
macroscópicos a partir de consideraciones microscópicas utilizando para ello
herramientas estadísticas junto a leyes mecánicas.
• La física estadística puede describir numerosos campos con una naturaleza
estocástica (reacciones nucleares, sistemas biológicos, químicos, neurológicos,
etc.).

8. • En medicina se utiliza el concepto de historia clínica para el registro de
datos sanitarios significativos de un paciente, que se ascienden hasta su
nacimiento o incluso a su herencia genética.
• La bioestadística, de forma general, es la aplicación de la estadística a la
biología. Debido a que las cuestiones a investigar en biología son de
naturaleza muy variada, por ejemplo, la medicina, ciencias agropecuarias y
forestales, la bioestadística ha difundido sus dominios para incluir cualquier
modelo cuantitativo, no sólo estadístico, que pueda ser usado para responder
a estas necesidades.
• Entre otras disciplinas.

9. División de la estadística para su estudio.
• Estas técnicas son tan variadas que los estadísticos, por lo general, las dividen
en dos grandes categorías:
Estadística
descriptiva y
Estadística
inferencial.

10. La estadística
descriptiva
Consiste en la presentación
de datos en forma de tablas
y gráficas
Esta comprende cualquier
actividad relacionada con los
datos y está diseñada para
resumir o descubrir los
mismos sin factores
pertinentes adicionales
La estadística
inferencial
Se deriva de muestras que
son subconjuntos de una
población con alguna
característica de interés
A partir de las observaciones
hechas a una parte de un
conjunto numeroso de
elementos, se infiere acerca
de las características que
posee la población.

11. Método estadístico con la investigación
científica.
• La ciencia , tecnología demandan de la aplicación del método científico para llevar a cabo su
desarrollo, donde la estadística es una de las herramientas matemáticas fundamentales, que apoya
al investigador en su proceso de indagación, investigación, búsqueda desde la perspectiva de la
filosofía analítica en el diseño del:
• 1. Planteamiento del problema.
• 2. Operacionalización del problema.
• 2.1. Formulación de hipótesis.
• 2.2. Operativización de conceptos teóricos.
• 2.3. Definición de unidades de análisis.
• 3. Diseño muestral.
• 4. Técnicas de análisis de datos.

12. Definición y clasificación de las variables.
Variable
Variables cuantitativas
Variables cualitativas o
atributos
Es una característica que se
asocia a los elementos de
una muestra o población.

13. Variables
cuantitativas
Discretas
sólo se miden por
medio de valores
puntuales
Por Ejemplo:
Numero de materias,
cantidad de médicos
en un hospital
Continuas
Pueden tomar
cualquier valor
intermedio entre dos
números, es decir,
intervalos.
Por Ejemplo: El peso
y la estatura de una
persona.

14. Variables cualitativas o
atributos:
Nominales:
Son aquellas que sólo admiten una mera
ordenación alfabética, pero no establecen
orden por su contenido. Por Ejemplo:
género, estado civil, color de cabello.
Son aquellas que sugieren una
ordenación. Por Ejemplo: Nivel de
estudio, posición de los ganadores de un
concurso; y
Ordinales:

15. Las variables también se pueden clasificar en:
Variables unidimensionales:
• Solo recogen información sobre
una característica. Por Ejemplo:
Edad de los alumnos de una
clase.
Variables Bidimensionales:
• Recogen información sobre dos
características de la población.
Por Ejemplo: Edad y estatura y
peso de los alumnos de una
clase.

16. Diferentes tipos de datos:
Datos Cualitativos:
Etiquetas o nombres que se
utilizan para identificar un
atributo de cada elemento. (se
utiliza la escala de medición
nominal y ordinal).
Datos Cuantitativos:
Son valores numéricos que indica
cuanto(s). (se emplea la escala de
intervalo o razón).
Datos Transversales:
Datos reunidos en el mismo o
aproximadamente el mismo
punto en el tiempo.
Datos de Serie de Tiempo:
Datos obtenidos en diversos
períodos sucesivos

17. Formas de presentar los datos.
*Tabuladamente.
*Gráficamente
*Mediante números que caracterizan al
grupo de datos.
Los datos obtenidos
se los puede
representar de
diferentes formas:

18. TABLAS DE FRECUENCIA
Según el número de observaciones y el rango de la variable, podemos clasificar las tablas de la siguiente manera:
Tablas de Tipo I:
EL tamaño de la población o muestra es pequeño. Por ejemplo: Las edades de 6 personas: 15, 18, 19, 21, 24, 28. Sólo de ordenan
de manera creciente o decreciente.
Tablas de tipo II:
El tamaño de la población o muestra es grande y el rango de la variable es pequeño. Por ejemplo:
El número diario de llamadas telefónicas realizadas en una casa durante 30 días, se encuentra tabulado así:
3 2 5 4 2 1
2 1 3 5 2 3
3 2 2 1 4 5
2 3 5 4 5 1
4 3 1 1 1 3

19. • Sea la variable el numero diario de llamadas, telefónicas, podemos observas
que el rango de la variable está entre 1 y 5 llamadas, y que el total de datos es
30 llamadas. Por lo tanto, la tabla de frecuencias se estructura:
• Ordenando los datos creciente o decreciente, luego se estructura la tabla de
frecuencia relacionando el conteo con un número (Frecuencia):
N° de llamadas Frecuencia
1
7
2
7
3
7
4
4
5
5
TOTAL 30

20. • Tablas de tipo III : llamada tabla de intervalos, el tamaño de la población o
muestra es grande y el rango de la variable es grande.
5 28 47 22 12 20
44 18 40 50 23 10
14 28 26 30 27 16
42 55 36 27 27 50
38 15 31 24 43 7

21. • Sea la variable la edad de las personas, observamos que los valores están
dispersos y que el rango de la variable está entre 5 y 55 por lo cual, si se
quiere elaborar una tabla, está debe ser de intervalos.
Intervalos Frecuencia
5 - 9 2
9 - 13 2
13 - 17 3
17 - 21 2
21 - 25 3
25 - 29 6
29 - 33 2
33 - 37 1
37 - 41 2
41 - 45 3
45 - 49 1
49 - 53 2
53 - 57 1
TOTAL 30

22. Tablas de distribución de frecuencias:
Frecuencia absoluta.- Es el número de veces que aparece dicho valor, como
resultado de la medición de la variable. Se denota por ʄ i
Frecuencia absoluta acumulada: Es el resultado de sumar la frecuencia
absoluta del valor correspondiente la frecuencia absoluta del valor anterior. Se
denota por Fi
Frecuencia relativa: Es el cociente entre la frecuencia absoluta y el tamaño
de la muestra o población: hi= ʄ i /N´, donde N= Tamaño de la muestra o
población. Se denota por hi.
Frecuencia relativa acumulada: Es el resultado de sumar a la frecuencia
relativa del valor correspondiente la frecuencia relativa del valor anterior. Se
denota por Hi.

24. Gráficos de representación.
Histograma: Es un gráfico de
barras (Sin espacio entre ellas),
formando por rectángulos, cuya
base está dada por la amplitud de
cada intervalo y cuyas alturas
corresponden a las frecuencias
(frecuencia absolutas o relativas)
alcanzadas por dichos intervalos.
Poligonal de frecuencias: Se
obtiene al unir las marcas de
clases con las frecuencias
respectivas, formando un par
ordenado.
Diagrama de tallo y hojas:
Este diagrama permite apreciar
la variabilidad o dispersión de
los datos.
Ojiva: Este gráfico se usa
representar la frecuencia
acumulada, absoluta o relativa.
Se lo obtiene uniendo
segmentos de recta que se
extienden entre los extremos de
las clases y usando los valores
de la frecuencia acumulada.

25. CONCLUSIONES
A lo largo de nuestra investigación hemos ido
descubriendo y cubriendo los objetivos
planteados desde el inicio.
En el primer capítulo donde fue el desarrollo de
nuestro trabajo se presentaron las bases de de
nuestro proyecto lo cual fue enfocada de
manera uniforme y ampliada a criterio de todos
nosotros cual era la información específica,
relevante y necesaria para este tipo de trabajo.
Este tipo de actividad se dio por la necesidad del ser
humano de mantener la información acerca del
comportamiento de algunas variables como la salud,
vitalidad, progreso, crecimiento, morbilidad en todos
los aspectos de los seres humanos, una gran
herramienta de apoyo para los investigadores que la
usan como herramienta y evaluación de patrones, para
la toma de decisiones acertadas para la humanidad o la
vida en general.
Este tipo de actividad se dio por la necesidad del ser
humano de mantener la información acerca del
comportamiento de algunas variables como la salud,
vitalidad, progreso, crecimiento, morbilidad en todos
los aspectos de los seres humanos, una gran
herramienta de apoyo para los investigadores que la
usan como herramienta y evaluación de patrones, para
la toma de decisiones acertadas para la humanidad o la
vida en general.
Como nos hemos visto obligados a estar físicamente en
un futuro las nuevas tecnologías para el aprendizaje
deben estar listas para los alumnos y poder desarrollar
de la misma manera como si lo estuviésemos haciendo
personalmente podríamos incluir las salas de chat y
hasta videos conferencias que nos acercan a una
situación física o presencial.

26. BIBLIOGRAFÍA
• Berenson M,.Levine D,.Krehbiel T., (2001) Estadística para administración (Segunda edición)
• Levein R,.RubinD.,Banderas M., Valle J, Gómez R., (2004) Estadística para administración y economía (Séptima
edición)
• Mason R., Lind D., Marchal W., (2002) Estadística para administración y economía (Décima edición)
• Triola Mario, (2004) Estadística (Novena edición)
• Webster, Allen (2000), Estadística aplicada a los negocios y la economía (Tercera edición)
• Espol (2006) , Fundamentos de matemáticas (Segunda Edición )