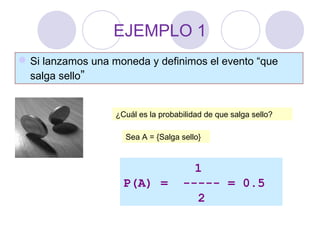
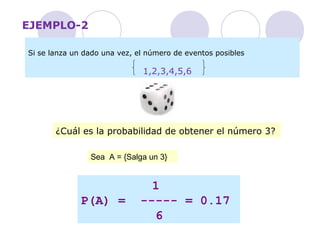
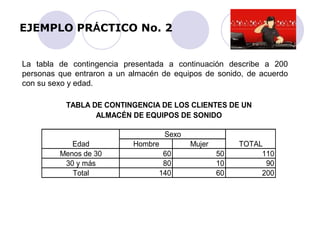
Este documento introduce los conceptos básicos de la teoría de la probabilidad. Explica que la probabilidad se refiere a la posibilidad de que ocurra un evento en particular o a su frecuencia relativa. Luego describe los tres enfoques para determinar la probabilidad: clásico a priori, clásico empírico y subjetivo. Finalmente, introduce conceptos como sucesos, operaciones con eventos como la multiplicación y la probabilidad condicional.