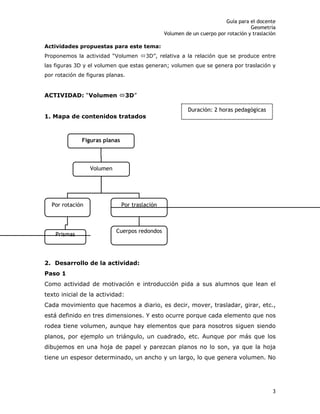
Este documento presenta una guía para docentes sobre el volumen de cuerpos generados por rotación y traslación de figuras planas. Incluye contenidos curriculares, aprendizajes esperados, recursos digitales y una actividad propuesta con ejercicios de cálculo de volúmenes de figuras tridimensionales como cilindros, conos y esferas.