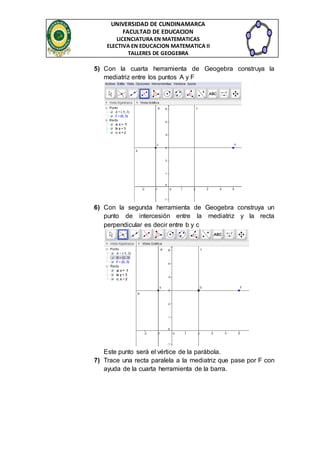
Este documento presenta una guía para un taller sobre secciones cónicas utilizando la herramienta Geogebra. Explica cómo construir geométricamente una circunferencia y una parábola, identificando sus partes como el centro, radio, diámetro y foco. También incluye ejercicios prácticos para que los estudiantes apliquen los procedimientos aprendidos y evalúen su comprensión de estos conceptos geométricos.