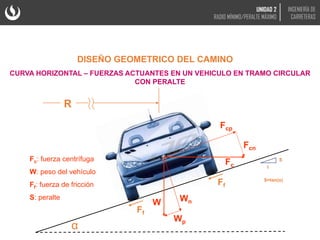
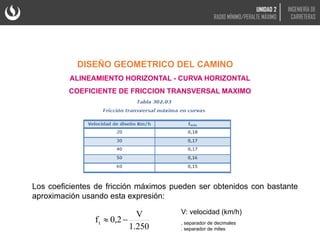
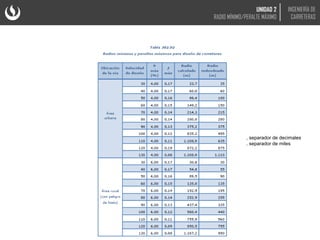
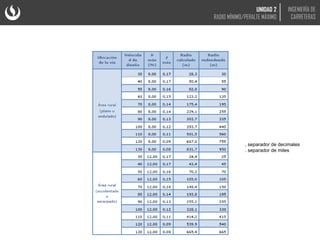
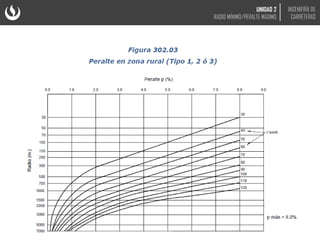
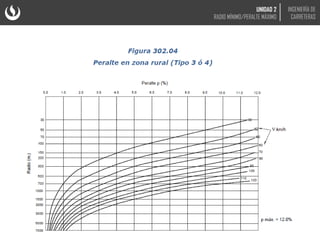
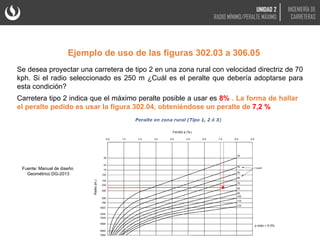
El documento trata sobre el diseño geométrico de curvas horizontales en carreteras. Explica que el peralte y el radio mínimo de una curva dependen de la velocidad de diseño, el coeficiente de fricción y fuerzas como la centrífuga. Incluye fórmulas y gráficas para calcular el peralte óptimo en función del radio de la curva y la velocidad.

1. UNIVERSIDAD PERUANA DE CIENCIAS APLICADAS
LAUREATE INTERNATIONAL UNIVERSITIES
INGENIERÍA DE CARRETERAS
UNIDAD 2
TRAMOS TANGENTES Y DISTANCIAS DE VISIBILIDAD
RADIO MÍNIMO Y PERALTE MÁXIMO
VISIBILIDAD EN CURVAS HORIZONTALES
CURVAS DE TRANSICIÓN
SOBRE ANCHOS
FACULTAD DE INGENIERÍA
CARRERA DE INGENIERÍA CIVIL

2. El aspecto crítico en el Alineamiento Horizontal está en el diseño de las curvas
horizontales donde los vehículos tienden a conservar el movimiento en línea
recta.
DISEÑO GEOMETRICO DEL CAMINO
ALINEAMIENTO HORIZONTAL – CURVA HORIZONTAL
Los vehículos permanecen en la curva
primeramente debido a la fricción
transversal entre el pavimento y sus
llantas, pero a veces no es suficiente por
lo que se da una inclinación a la calzada
llamada peralte.
UNIDAD 2
RADIO MÍNIMO/PERALTE MÁXIMO
INGENIERÍA DE
CARRETERAS

3. Fc: fuerza centrífuga
W: peso del vehículo
Ff: fuerza de fricción
S: peralte
DISEÑO GEOMETRICO DEL CAMINO
CURVA HORIZONTAL – FUERZAS ACTUANTES EN UN VEHICULO EN TRAMO CIRCULAR
CON PERALTE
Fcp
Fcn
Fc
W
Ff
Wn
Wp
Ff
R
α
S
1
S=tan(α)
UNIDAD 2
RADIO MÍNIMO/PERALTE MÁXIMO
INGENIERÍA DE
CARRETERAS

4. • La fuerza de fricción Ff se opone al deslizamiento lateral entre las llantas y
el pavimento.
• A velocidades altas esta fuerza no es suficiente para impedir el
deslizamiento.
• Es necesario el peralte.
• En la figura, la resultante paralela al pavimento (Fcp – Wp) actúa hacia la
derecha, y debe ser contrarrestada por la fuerza de fricción transversal Ff
que actúa hacia la izquierda.
DISEÑO GEOMETRICO DEL CAMINO
CURVA HORIZONTAL – FUERZAS ACTUANTES EN UN VEHICULO EN TRAMO CIRCULAR
CON PERALTE
UNIDAD 2
RADIO MÍNIMO/PERALTE MÁXIMO
INGENIERÍA DE
CARRETERAS

5. α
DISEÑO GEOMETRICO DEL CAMINO
CURVA HORIZONTAL – FUERZAS ACTUANTES EN UN VEHICULO EN TRAMO CIRCULAR
CON PERALTE
W
tanα
F
Wtanα
F
cosα
entre
dividiendo
Wcosα
senα
F
Wsenα
cosα
F
W
F
W
F
)
W
(F
W
F
:
tanto
lo
por
)
W
(F
F
x
normal
fuerza
F
:
que
sabe
se
pero
F
)
W
(F
c
c
t
c
c
n
cn
p
cp
t
t
n
cn
p
cp
t
n
cn
f
t
f
f
p
cp

















f
f
f
f
f (ft: coeficiente de fricción transversal)
UNIDAD 2
RADIO MÍNIMO/PERALTE MÁXIMO
INGENIERÍA DE
CARRETERAS

6. Fc: fuerza centrífuga
m: masa del vehículo
a: aceleración radial
DISEÑO GEOMETRICO DEL CAMINO
CURVA HORIZONTAL – FUERZAS ACTUANTES EN UN VEHICULO EN TRAMO CIRCULAR
CON PERALTE
Modelación Matemática:
Fc = ma (1)
m = W/g (2)
a = V2/R (3)
Reemplazando (2) y (3) 3n (1)
(4)
gR
WV
F
2
c 
UNIDAD 2
RADIO MÍNIMO/PERALTE MÁXIMO
INGENIERÍA DE
CARRETERAS

7. Reemplazando el valor de Fc (ecuación 4) y tan por la sobreelevación S,
resulta:
DISEÑO GEOMETRICO DEL CAMINO
CURVA HORIZONTAL – FUERZAS ACTUANTES EN UN VEHICULO EN TRAMO CIRCULAR
CON PERALTE
(5)
S)
g(
V
R
ó
gR
V
S
0)
S
(
S
de
normales
valores
para
S)
(1
gR
V
S
1
S
gR
V
S
gR
V
W
S
gR
WV
WS
gR
WV
t
2
2
t
t
t
2
t
2
2
2
2
t














f
f
f
f
f
f
UNIDAD 2
RADIO MÍNIMO/PERALTE MÁXIMO
INGENIERÍA DE
CARRETERAS

8. Expresando la velocidad V en km/h, el radio R en metros y sustituyendo g por
9.81 m/s2, se tiene:
DISEÑO GEOMETRICO DEL CAMINO
CURVA HORIZONTAL – FUERZAS ACTUANTES EN UN VEHICULO EN TRAMO CIRCULAR
CON PERALTE
V: Km/h
R: m
S)
127(f
V
R
t
2


ft: coeficiente de fricción transversal
S: peralte (en decimal)
UNIDAD 2
RADIO MÍNIMO/PERALTE MÁXIMO
INGENIERÍA DE
CARRETERAS

9. DISEÑO GEOMETRICO DEL CAMINO
ALINEAMIENTO HORIZONTAL - CURVA HORIZONTAL
COEFICIENTE DE FRICCION TRANSVERSAL
• Los valores de “ft” varían entre 0,5 y 0,35 según estudios, pero los valores
máximos de diseño según AASHTO, en pavimento húmedo varían entre 0,17
y 0,09 de acuerdo a la velocidad.
• El coeficiente de fricción Transversal varia de acuerdo al tipo de superficie
del pavimento (Asfalto, concreto o superficie granular) y a la fricción ejercida
por los neumáticos al pasar por la curva circular
UNIDAD 2
RADIO MÍNIMO/PERALTE MÁXIMO
INGENIERÍA DE
CARRETERAS

10. DISEÑO GEOMETRICO DEL CAMINO
ALINEAMIENTO HORIZONTAL - CURVA HORIZONTAL
COEFICIENTE DE FRICCION TRANSVERSAL MAXIMO
Los coeficientes de fricción máximos pueden ser obtenidos con bastante
aproximación usando esta expresión:
V: velocidad (km/h)
1.250
V
0,2
ft 
 , separador de decimales
. separador de miles
UNIDAD 2
RADIO MÍNIMO/PERALTE MÁXIMO
INGENIERÍA DE
CARRETERAS

11. Los valores de peralte y coeficiente de fricción máximo permiten obtener los
radios mínimos absolutos para una curva circular.
DISEÑO GEOMETRICO DEL CAMINO
ALINEAMIENTO HORIZONTAL - CURVA HORIZONTAL
RADIO MINIMO ABSOLUTO
Es importante recordar que el valor de peralte máximo depende del tipo de
carretera según la orografía (1, 2, 3, 4) zona con hielo y zona urbana.
)
S
127(f
V
R
max
máx
t
2
mín


V: Km/h
R: m
ft: coeficiente de fricción transversal
S: peralte (en decimal)
UNIDAD 2
RADIO MÍNIMO/PERALTE MÁXIMO
INGENIERÍA DE
CARRETERAS

12. • Tiene un valor máximo hallado de experiencias prácticas.
• El valor máximo esta sujeto a diferentes condiciones, como: condiciones de
clima, nieve, hielo, forma del terreno, área rural o urbana y flujo de vehículos
a baja velocidad.
• Por lo mencionado anteriormente se deduce que no hay un valor máximo
universal para el peralte, sino que depende de cada situación específica.
Valores máximos
de peralte (Smax)
DISEÑO GEOMETRICO DEL CAMINO
ALINEAMIENTO HORIZONTAL - CURVA HORIZONTAL
PERALTE O SOBREELEVACION
S = 12% para área rural (accidentado o escarpado)
S = 8% para área rural (plano o ondulado)
S = 6% para área rural con nieve o hielo
S = 4% para área urbanas
UNIDAD 2
RADIO MÍNIMO/PERALTE MÁXIMO
INGENIERÍA DE
CARRETERAS

13. , separador de decimales
. separador de miles
UNIDAD 2
RADIO MÍNIMO/PERALTE MÁXIMO
INGENIERÍA DE
CARRETERAS

14. , separador de decimales
. separador de miles
UNIDAD 2
RADIO MÍNIMO/PERALTE MÁXIMO
INGENIERÍA DE
CARRETERAS

15. En la selección de un radio existen diversas posibilidades dependiendo del
peralte y el coeficiente de fricción seleccionados. Hay casos extremos, uno de
ellos es cuando hay radios muy amplios que no requieren de peralte alguno y
el otro es cuando el peralte y el coeficiente de fricción son máximos
determinando el radio mínimo absoluto (más pequeño de todos) que podría
usarse .
DISEÑO GEOMETRICO DEL CAMINO
ALINEAMIENTO HORIZONTAL - CURVA HORIZONTAL
CAMBIO DE PERALTE Y RADIO PARA UNA VELOCIDAD DIRECTRIZ
α
UNIDAD 2
RADIO MÍNIMO/PERALTE MÁXIMO
INGENIERÍA DE
CARRETERAS

16. Entre los casos extremos mencionados anteriormente el peralte y fricción
varían gradualmente hasta alcanzar su valor máximo respectivo. La variación
que experimentan podría ser estimada en base a 5 procedimientos
mencionados en el libro de la AASHTO. A continuación se mencionan los
procedimientos pero se recalca que el 5to es el utilizado en la actualidad.
1. El peralte y el coeficiente de fricción son directamente proporcionales a la
inversa del radio (curvatura).
2. Cuando un vehículo viaja a la velocidad de diseño todo el efecto de la fuerza
centrífuga es tomado por la fricción que varía en forma lineal hasta que
alcanza su valor máximo; después de esto, para situaciones más adversas
la fricción permanece constante (ft máx ) y aparece luego el peralte, para
tomar el efecto remanente, hasta que alcanza su valor máximo (S máx).
DISEÑO GEOMETRICO DEL CAMINO
ALINEAMIENTO HORIZONTAL - CURVA HORIZONTAL
CAMBIO DE PERALTE Y RADIO PARA UNA VELOCIDAD DIRECTRIZ
UNIDAD 2
RADIO MÍNIMO/PERALTE MÁXIMO
INGENIERÍA DE
CARRETERAS

17. 3. Cuando un vehículo viaja a la velocidad de diseño todo el efecto de la fuerza
centrífuga es tomado por el peralte que varía en forma lineal hasta que
alcanza su valor máximo; después de esto, para situaciones más adversas
el peralte permanece constante (Smáx ) y aparece luego la fricción, para
tomar el efecto remanente, hasta que alcanza su valor máximo (ft máx).
4. El método 4 es el mismo que el método 3, excepto que es basado en la
velocidad de circulación (running speed) en vez de la velocidad de diseño.
DISEÑO GEOMETRICO DEL CAMINO
ALINEAMIENTO HORIZONTAL - CURVA HORIZONTAL
CAMBIO DE PERALTE Y RADIO PARA UNA VELOCIDAD DIRECTRIZ
UNIDAD 2
RADIO MÍNIMO/PERALTE MÁXIMO
INGENIERÍA DE
CARRETERAS

18. El uso del método 5 y la ecuación (**)
.
DISEÑO GEOMETRICO DEL CAMINO
ALINEAMIENTO HORIZONTAL - CURVA HORIZONTAL
CAMBIO DE PERALTE Y RADIO PARA UNA VELOCIDAD DIRECTRIZ
5. El peralte y coeficiente de fricción transversal presentan una relación
curvilínea en relación con la inversa del radio, con valores entre los
métodos 1 y 3.
)
S
127(f
V
R
max
máx
t
2
mín


(**)
Es posible la construcción de las figuras 302.02 a 302.05 del Manual de
Diseño Geométrico de Carreteras DG 2013.
UNIDAD 2
RADIO MÍNIMO/PERALTE MÁXIMO
INGENIERÍA DE
CARRETERAS

19. UNIDAD 2
RADIO MÍNIMO/PERALTE MÁXIMO
INGENIERÍA DE
CARRETERAS

20. UNIDAD 2
RADIO MÍNIMO/PERALTE MÁXIMO
INGENIERÍA DE
CARRETERAS

21. UNIDAD 2
RADIO MÍNIMO/PERALTE MÁXIMO
INGENIERÍA DE
CARRETERAS

22. UNIDAD 2
RADIO MÍNIMO/PERALTE MÁXIMO
INGENIERÍA DE
CARRETERAS

23. Ejemplo de uso de las figuras 302.03 a 306.05
Se desea proyectar una carretera de tipo 2 en una zona rural con velocidad directriz de 70
kph. Si el radio seleccionado es 250 m ¿Cuál es el peralte que debería adoptarse para
esta condición?
Carretera tipo 2 indica que el máximo peralte posible a usar es 8% . La forma de hallar
el peralte pedido es usar la figura 302.04, obteniéndose un peralte de 7,2 %
Fuente: Manual de diseño
Geométrico DG-2013
UNIDAD 2
RADIO MÍNIMO/PERALTE MÁXIMO
INGENIERÍA DE
CARRETERAS

24. Elección del radio de la curva circular simple
• No hay una regla fija , pero los radios de las curvas deben ser lo más
grandes posibles adaptándose a la topografía de la zona.
• Se recomienda no proyectar dos curvas horizontales en el mismo sentido
cuando entre ellas exista una tangente corta, siendo preferible emplear una
sola curva que abarque a las dos.
• Cuando se pasa de una zona a otra con diferente velocidad directriz, el
cambio debe ser gradual; por ejemplo no es recomendable una curva
cerrada al final de un largo tramo recto.
• Los radios de las curvas consecutivas deben asegurar que no exista una
variación muy grande entre las velocidades que pueden alcanzarse en ellas.
• Sólo se usarán radios mínimos cuando su uso sea estrictamente obligatorio
según la topografía y las condiciones de operación.
ALINEAMIENTO HORIZONTAL - CURVA HORIZONTAL
ELECCION DEL RADIO DE LA CURVA CIRCULAR SIMPLE
UNIDAD 2
RADIO MÍNIMO/PERALTE MÁXIMO
INGENIERÍA DE
CARRETERAS

25. CURVA CIRCULAR
DISEÑO GEOMETRICO DEL CAMINO
ALINEAMIENTO HORIZONTAL
Fuente: Quintana y Altez
UNIDAD 2
RADIO MÍNIMO/PERALTE MÁXIMO
INGENIERÍA DE
CARRETERAS

26. CONCLUSIONES
UNIDAD 2
RADIO MÍNIMO/PERALTE MÁXIMO
INGENIERÍA DE
CARRETERAS