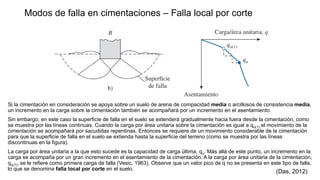
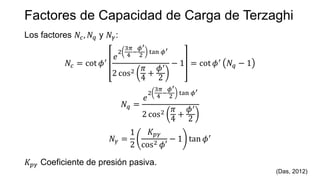
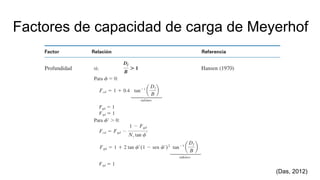
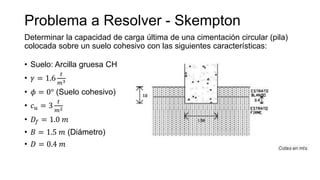
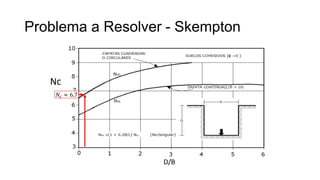
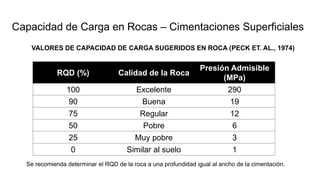
Este documento presenta los modos de falla en cimentaciones según Vesic (1973): falla general por corte, falla local por corte y falla por punzonamiento. Explica la teoría de capacidad de carga de Terzaghi (1943), Skempton y Meyerhof, incluyendo factores de capacidad, superficies de falla y ecuaciones para calcular la carga última en cimentaciones. Finalmente, discute factores como la forma, inclinación de carga y resistencia al corte a lo largo de la superficie de falla.

1. Capacidad de Carga
Ing. Rafael Ortiz Hernández
Geotecnia
División de Investigación y Posgrado Facultad de Ingeniería
Universidad Autónoma de Querétaro

2. Generalidades
Modos de Falla
Carga última
Carga permisible

3. Modos de falla en cimentaciones
Existen 3 modos de falla, de acuerdo a Vesic (1973):
• Falla general por corte
• Falla local por corte
• Falla de corte por punzonamiento
(Das, 2012)

4. Modos de falla en cimentaciones – Falla general por corte
Considere un cimentación corrida con un ancho B que se apoya sobre la superficie de una arena densa o suelo
cohesivo rígido.
Ahora, si se aplica una carga gradualmente a la cimentación, el asentamiento se incrementará. La variación de la
carga por área unitaria (q) sobre la cimentación con el asentamiento de la cimentación.
En cierto punto, cuando la carga por área unitaria es igual a qu, ocurrirá una falla repentina en el suelo que
soporta la cimentación y la superficie de falla en el suelo se extenderá hasta la superficie del terreno.
A esta carga por área unitaria, qu, suele referírsele como capacidad de carga última de la cimentación. Cuando
este tipo de falla repentina ocurre en el suelo, se denomina falla general por corte.
(Das, 2012)

5. Modos de falla en cimentaciones – Falla local por corte
Si la cimentación en consideración se apoya sobre un suelo de arena de compacidad media o arcillosos de consistencia media,
un incremento en la carga sobre la cimentación también se acompañará por un incremento en el asentamiento.
Sin embargo, en este caso la superficie de falla en el suelo se extenderá gradualmente hacia fuera desde la cimentación, como
se muestra por las líneas continuas. Cuando la carga por área unitaria sobre la cimentación es igual a qu(1) el movimiento de la
cimentación se acompañará por sacudidas repentinas. Entonces se requiere de un movimiento considerable de la cimentación
para que la superficie de falla en el suelo se extienda hasta la superficie del terreno (como se muestra por las líneas
discontinuas en la figura).
La carga por área unitaria a la que esto sucede es la capacidad de carga última, qu. Más allá de este punto, un incremento en la
carga se acompaña por un gran incremento en el asentamiento de la cimentación. A la carga por área unitaria de la cimentación,
qu(1), se le refiere como primera carga de falla (Vesic, 1963). Observe que un valor pico de q no se presenta en este tipo de falla,
lo que se denomina falla local por corte en el suelo.
(Das, 2012)

6. Modos de falla en cimentaciones – Falla corte por punzonamiento
Si la cimentación está soportada por un suelo muy suelto, la gráfica carga-asentamiento será como la
de la figura. En este caso, la superficie de falla en el suelo no se extenderá hasta la superficie del
terreno. Más allá de la carga última de falla, qu, la gráfica carga-asentamiento será muy pronunciada y
prácticamente lineal.
Este tipo de falla en el suelo se denomina falla de corte por punzonamiento.
(Das, 2012)

7. Modos de falla en cimentaciones – Vesic
Los experimentos de Vesic
(1973) en cimentaciones
desplantadas sobre rellenos de
arena de diferentes
compacidades le llevo a hacer
una clasificación de acuerdo a la
densidad relativa del material de
apoyo y al empotramiento de la
cimentación.
(Das, 2012)

8. Capacidad de carga última
La carga por área unitaria de la cimentación a la que ocurre la
falla por corte en un suelo se denomina capacidad de carga
última 𝑞𝑢.

9. Capacidad de carga permisible
Esta capacidad de carga es la permisible de acuerdo a dos
condiciones:
• Un factor aplicado a la capacidad de carga última: 𝑞𝑝𝑒𝑟𝑚 =
𝑞𝑢
𝐹𝑆
• La carga aplicada que llega a un asentamiento máximo
establecido por el proyecto.
Usualmente es la segunda condición la que domina la carga
permisible.

10. Teoría de Capacidad de Terzaghi

11. Teoría de Capacidad de Terzaghi
Terzaghi (1943) fue el primero en presentar una teoría completa
para evaluar la capacidad de carga última de cimentaciones
aproximadamente superficiales.
De acuerdo con su teoría, una cimentación es superficial si su
profundidad, Df, es menor que o igual a su ancho.
(Das, 2012)

12. Teoría de Capacidad de Terzaghi
Terzaghi sugirió que para una cimentación continua o corrida (es decir,
cuando su relación ancho a longitud tiende a cero), la superficie de falla en
el suelo ante carga última caso de falla general es el siguiente:
(Das, 2012)

13. Teoría de Capacidad de Terzaghi
El efecto del suelo arriba del fondo de la cimentación también se
puede suponer que se reemplaza por una sobrecarga
equivalente, 𝑞 = 𝛾𝐷𝑓.
(Das, 2012)

14. Teoría de Capacidad de Terzaghi
La zona de falla bajo la cimentación se puede separar en tres partes:
1. La zona triangular ACD inmediatamente abajo de la cimentación.
2. Las zonas de radiales de corte ADF y CDE, con las curvas DE y DF como arcos de una espiral logarítmica.
3. Dos zonas triangulares pasivas de Rankine FH y CEG.
Los ángulos CAD y ACD se suponen iguales al ángulo de fricción del suelo 𝜙′. Observe que, con el reemplazo
del suelo arriba del fondo de la cimentación por una sobrecarga equivalente q, se ignoró la resistencia cortante
del suelo a lo largo de las superficies de falla GI y HJ. (Das, 2012)

15. Teoría de Capacidad de Terzaghi
Aplicando un análisis de equilibrio, Terzaghi expresó la Capacidad de
carga última para una zapata corrida en la forma:
𝑞𝑢 = 𝑐′𝑁𝑐 + 𝑞𝑁𝑞 +
1
2
𝛾𝐵𝑁𝛾
Donde:
𝑐′ Intercepto de cohesión del suelo
𝛾 Peso especifico del suelo
𝑞 = 𝛾𝐷𝑓 Sobrecarga por el terreno
𝑁𝑐, 𝑁𝑞, 𝑁𝛾 Factores de capacidad de carga adimensionales 𝑓 𝜙′
(Das, 2012)

16. Factores de Capacidad de Carga de Terzaghi
Los factores 𝑁𝑐, 𝑁𝑞 y 𝑁𝛾:
𝑁𝑐 = cot 𝜙′
𝑒
2
3𝜋
4
−
𝜙′
2
tan 𝜙′
2 cos2 𝜋
4
+
𝜙′
2
− 1 = cot 𝜙′ 𝑁𝑞 − 1
𝑁𝑞 =
𝑒
2
3𝜋
4
−
𝜙′
2
tan 𝜙′
2 cos2 𝜋
4
+
𝜙′
2
𝑁𝛾 =
1
2
𝐾𝑝𝛾
cos2 𝜙′
− 1 tan 𝜙′
𝐾𝑝𝛾 Coeficiente de presión pasiva.
(Das, 2012)

17. Factores de Capacidad de Carga de Terzaghi
(Das, 2012)

18. Teoría de Capacidad de Terzaghi
Zapata corrida:
𝑞𝑢 = 𝑐′
𝑁𝑐 + 𝑞𝑁𝑞 +
1
2
𝛾𝐵𝑁𝛾
Zapata cuadrada:
𝑞𝑢 = 1.3𝑐′𝑁𝑐 + 𝑞𝑁𝑞 + 0.4𝛾𝐵𝑁𝛾
Zapata circular:
𝑞𝑢 = 1.3𝑐′𝑁𝑐 + 𝑞𝑁𝑞 + 0.3𝛾𝐵𝑁𝛾
(Das, 2012)

19. Teoría de Capacidad de Terzaghi
Para falla local por corte:
Zapata corrida:
𝑞𝑢 =
2
3
𝑐′𝑁𝑐
′ + 𝑞𝑁𝑞
′ +
1
2
𝛾𝐵𝑁𝛾
′
Zapata cuadrada:
𝑞𝑢 = 0.867𝑐′𝑁𝑐
′ + 𝑞𝑁𝑞
′ + 0.4𝛾𝐵𝑁𝛾
′
Zapata circular:
𝑞𝑢 = 0.867𝑐′
𝑁𝑐
′
+ 𝑞𝑁𝑞
′
+ 0.3𝛾𝐵𝑁𝛾
′
(Das, 2012)

20. Factores Modificados de Capacidad de Carga de Terzaghi
(Das, 2012)

21. Teoría de Capacidad de Skempton

22. Teoría de Capacidad de Skempton
Skempton encontró que en materiales de grano fino (arcillas) el
valor del factor de capacidad de carga 𝑁𝑐 no es independiente de
la profundidad de desplante, 𝑁𝑐 crece al aumentar la profundidad
de desplante del cimiento
Si bien este crecimiento no es ilimitado, de manera que 𝑁𝑐
permanece constante a una cierta profundidad de desplante.
𝑞𝑢𝑙𝑡 = 𝑞 + 𝑐𝑁𝑐
(Acevedo, 2014)

23. Teoría de Capacidad de Skempton
𝑞𝑢𝑙𝑡 = 𝑞 + 𝑐𝑢𝑁𝑐
Dónde:
𝑞 Sobrecarga por encima de la cimentación (𝑞 = 𝛾𝐷𝑓)
𝑐𝑢 Cohesión no drenada del material de desplante
𝑁𝑐 Factor de capacidad de carga que toma en cuenta la
resistencia al corte que aporta la prolongación de la
superficie de falla por encima del nivel de desplante 𝐷𝑓.

24. Factor de Capacidad de Skempton
Para una zapata corrida:
𝑁𝑐 = 5.14 1 + 0.2
𝐷𝑓
𝐵
(Solo valida hasta
𝐷𝑓
𝐵
≤ 2.5, después se vuelve constante)
Para una zapata cuadrada o circular:
𝑁𝑐 = 6.168 1 + 0.2
𝐷𝑓
𝐵
Para una zapata rectangular de ancho B y Longitud L:
𝑁𝑐𝑟 = 5.14 1 + 0.2
𝐷𝑓
𝐵
1 + 0.2
𝐵
𝐿 (Acevedo, 2014)

25. Factor de Capacidad de Skempton
(Acevedo, 2014)

26. Teoría de Capacidad de Skempton
• La teoría de Skempton es adecuada para cimentaciones en
condiciones UU saturadas (𝜙 = 0), Sean superficiales o
profundas, incluyendo el calculo de cilindros y pilotes.
• 𝑁𝑐 crece al aumentar 𝐷𝑓 hasta alcanzar un valor límite para una
relación D/B=4
• Para una zapata corrida (L/B= ∞) 5.14 ≤ 𝑁𝑐 ≤ 7.50
• Para una cimentación cuadrada o circular 6.20 ≤ 𝑁𝑐 ≤ 9.00
(Acevedo, 2014)

27. Teoría de Capacidad de Meyerhof

28. Teoría de Capacidad de Meyerhof
Las ecuaciones de la capacidad de carga última de Terzaghi son
sólo para cimentaciones continuas, cuadradas y circulares; no
abordan el caso de cimentaciones rectangulares (0 <
𝐵
𝐿
< 1).
(Das, 2012)

29. Teoría de Capacidad de Meyerhof
Además, las ecuaciones no toman en cuenta la resistencia
cortante a lo largo de la superficie de falla en el suelo arriba del
fondo de la cimentación (la parte de la superficie de falla
marcada como GI y HJ).
(Das, 2012)

30. Teoría de Capacidad de Meyerhof
Además, la carga sobre la cimentación puede estar inclinada.
Para tomar en cuenta todos estos factores, Meyerhof (1963)
sugirió la forma siguiente de la ecuación general de la capacidad
de carga:
𝑞𝑢 = 𝑐′𝑁𝑐𝐹𝑐𝑠𝐹𝑐𝑑𝐹𝑐𝑖 + 𝑞𝑁𝑞𝐹𝑞𝑠𝐹𝑞𝑑𝐹𝑞𝑖 +
1
2
𝛾𝐵𝑁𝛾𝐹𝛾𝑠𝐹𝛾𝑑𝐹𝛾𝑖
(Das, 2012)

31. Teoría de Capacidad de Meyerhof
𝑞𝑢 = 𝑐′𝑁𝑐𝐹𝑐𝑠𝐹𝑐𝑑𝐹𝑐𝑖 + 𝑞𝑁𝑞𝐹𝑞𝑠𝐹𝑞𝑑𝐹𝑞𝑖 +
1
2
𝛾𝐵𝑁𝛾𝐹𝛾𝑠𝐹𝛾𝑑𝐹𝛾𝑖
Dónde:
𝑐′ Cohesión aparente
𝑞 Esfuerzo efectivo al nivel del fondo de la cimentación
𝛾 Peso específico del suelo
𝐵 Ancho de la cimentación (diámetro en cimentación circular)
(Das, 2012)

32. Teoría de Capacidad de Meyerhof
𝑞𝑢 = 𝑐′𝑁𝑐𝐹𝑐𝑠𝐹𝑐𝑑𝐹𝑐𝑖 + 𝑞𝑁𝑞𝐹𝑞𝑠𝐹𝑞𝑑𝐹𝑞𝑖 +
1
2
𝛾𝐵𝑁𝛾𝐹𝛾𝑠𝐹𝛾𝑑𝐹𝛾𝑖
Dónde:
𝑁𝑐, 𝑁𝑞, 𝑁𝛾 Factores de capacidad de carga
𝐹𝑐𝑠, 𝐹𝑞𝑠, 𝐹𝛾𝑠 Factores de forma (shape)
𝐹𝑐𝑑, 𝐹𝑞𝑑, 𝐹𝛾𝑑 Factores de profundidad (depth)
𝐹𝑐𝑖, 𝐹𝑞𝑖, 𝐹𝛾𝑖 Factores de inclinación de la carga (inclination)
(Das, 2012)

33. Factores de capacidad de carga de Meyerhof
En 𝑁𝑞:
𝑁𝑞 = tan2 45° +
𝜙′
2
𝑒𝜋 tan 𝜙′
En 𝑁𝑐:
𝑁𝑐 = 𝑁𝑞 − 1 cot 𝜙′
En 𝑁𝛾:
𝑁𝛾 = 2 𝑁𝑞 + 1 tan 𝜙′
(Das, 2012)

34. Factores de capacidad de carga de Meyerhof
(Das, 2012)

35. Factores de capacidad de carga de Meyerhof
(Das, 2012)

36. Factores de capacidad de carga de Meyerhof
(Das, 2012)

37. Factores de capacidad de carga de Meyerhof
(Das, 2012)

38. Factores de capacidad de carga de Meyerhof
(Das, 2012)

39. Problemas para resolver

40. Problemas a resolver
Recomiendo hacer los siguientes ejemplos del libro de Das:
• Ejemplo 3.1 (Terzaghi con Factor de Seguridad)
• Ejemplo 3.2 (Meyerhof)
• Ejemplo 3.3 (Meyerhof con agua)

41. Problema a Resolver - Skempton
Determinar la capacidad de carga última de una cimentación circular (pila)
colocada sobre un suelo cohesivo con las siguientes características:
• Suelo: Arcilla gruesa CH
• 𝛾 = 1.6
𝑡
𝑚3
• 𝜙 = 0° (Suelo cohesivo)
• 𝑐𝑢 = 3
𝑡
𝑚2
• 𝐷𝑓 = 1.0 𝑚
• 𝐵 = 1.5 𝑚 (Diámetro)
• 𝐷 = 0.4 𝑚

42. Problema a Resolver - Skempton
Se calcula D/B:
𝐷
𝐵
=
0.4 𝑚
1.5 𝑚
= 0.27 < 2.5
Se utiliza la formula para 𝑁𝑐:
𝑁𝑐 = 5.14 1 + 0.2
𝐷𝑓
𝐵
1.2 = 5.14 1 + 0.2 0.27 1.02
𝑁𝑐 = 6.501

43. Problema a Resolver - Skempton
𝑁𝑐 ≈ 6.7

44. Problema a Resolver - Skempton
Se calcula la capacidad de carga última:
𝑞𝑢 = 𝑐𝑢𝑁𝑐 + 𝛾𝑞𝐷𝑓
𝑞𝑢 = 3
𝑡
𝑚2
6.501 + 1.6
𝑡
𝑚2
1.0 𝑚
𝑞𝑢 = 19.503
𝑡
𝑚2
+ 1.6
𝑡
𝑚2
𝑞𝑢 = 21.103
𝑡
𝑚2

45. Valores reportados de
Capacidad de Carga

46. Valores reportados de Capacidad de Carga
(Briaud, 2013)
Valores admisibles, donde la capacidad de carga esta regulada por asentamientos.

47. Capacidad de Carga de Pilas

48. Capacidad de Carga de Pilas
Las pilas de cimentación obtienen su capacidad de carga por
tres mecanismos:
• Por punta, al apoyarse en un estrato firme y competente de
espesor adecuado.
• Por fuste, al tener resistencia del material que rodea a la pila.
• Una combinación de ambos, punta y fuste.
(SMIG, 2001)

49. Capacidad de Carga de Pilas
La capacidad de carga admisible de una pila se obtiene con la
siguiente formula:
𝑞𝑎𝑑𝑚 =
𝑄𝑝
𝐹𝑆𝑝
+
𝑄𝑓
𝐹𝑆𝑓
Dónde:
𝑄𝑝 Resistencia en punta de la pila
𝑄𝑓 Resistencia en fuste de la pila
𝐹𝑆𝑝, 𝐹𝑆𝑓 Factores de seguridad para cada tipo de resistencia
(SMIG, 2001)

50. Capacidad de Carga de Pilas
Existen 2 métodos tradicionales para el calculo de la capacidad
de carga en fuste y punta en pilas:
• Suelos de grano fino (cohesivos) - Método 𝛼
• Suelos de grano grueso (friccionantes) - Método 𝛽
(SMIG, 2001)

51. Capacidad de Carga de Pilas – Método 𝛼
En punta:
𝑄𝑝 = 𝑐𝑢𝑁𝑐
′𝐴𝑝
𝑄𝑝 Capacidad de carga última de una pila por punta.
𝑐𝑢 Resistencia al corte no drenado.
𝑁𝑐
′
Coeficiente de capacidad de carga
(7 para diámetros 0.5 – 1.0 m y 6 para diámetros > 1.0 m)
𝐴𝑝 Área de la punta de la pila
(SMIG, 2001)

52. Capacidad de Carga de Pilas – Método 𝛼
En fuste:
𝑄𝑠 = 𝛼𝐶𝑢𝑠𝐴𝑠
𝑄𝑠 Capacidad de carga última de una pila por fricción lateral.
𝛼 Factor de adherencia, valorado entre 0.2 a 0.4.
𝑐𝑢𝑠 Resistencia al corte no drenado, limitado a 100 kPa
𝐴𝑠 Área lateral del fuste.
(SMIG, 2001)

53. Capacidad de Carga de Pilas – Método 𝛽
En punta:
𝑄𝑝 = 𝑞𝑝𝐴𝑝; 𝑞𝑝 = 𝑝𝑜
′ 𝑁𝑞
′
𝑄𝑝 Capacidad de carga última de una pila por punta.
𝑞𝑝 Capacidad por punta unitaria.
𝑝𝑜
′
Presión efectiva vertical al nivel de desplante de la pila.
𝑁𝑞
′ Factor de capacidad de carga (Brinch Hansen/Meyerhof)
𝐴𝑝 Área de la punta de la pila
(SMIG, 2001)

54. Capacidad de Carga
de Pilas – Método 𝛽
𝑁𝑞
′ Factor de capacidad de carga
(Brinch Hansen/Meyerhof)
(SMIG, 2001)

55. Capacidad de Carga de Pilas – Método 𝛽
En fuste:
𝑄𝑠 = 𝛽𝑝𝑜𝑠
′
𝐴𝑠; 𝛽 = 𝐾𝑠 tan 𝛿
𝑄𝑠 Capacidad de carga última de una pila por fricción lateral.
𝐾𝑠 Relación entre esfuerzos efectivos horizontales y verticales.
(𝐾𝑠 = 0.7 si 𝐿𝑠 < 8 m, 0.6 si 𝐿𝑠 de 8 – 12 m y 0.5 si 𝐿𝑠 > 12 m)
tan 𝛿 Coeficiente de fricción lateral pila/suelo.
(𝛿 = 𝜙′ − 3°)
𝑝𝑜𝑠
′ Presión vertical efectiva promedio a lo largo del pilote
𝐴𝑆 Área lateral del fuste.
(SMIG, 2001)

56. “Hacer una cimentación profunda es un acto de fe”
– Manuel Jesús Mendoza López
II-UNAM
Conferencia Magistral
5° Simposio Internacional de Cimentaciones Profundas
CDMX, México
Incertidumbre en las condiciones de sitio.
Incertidumbre en las mediciones de parámetros geotécnicos.
Incertidumbre en la capacidad de carga.
Incertidumbre en las consideraciones de carga.
Incertidumbre en la calidad de los materiales.
Incertidumbre en el proceso constructivo.
Incertidumbre en el comportamiento a largo plazo.
Ignoramus et ignorabimus

57. Manual de Cimentaciones Profundas
Lo más novedoso y el estado del arte
en calculo de capacidad de carga en
cimentaciones con métodos analíticos
y métodos de pruebas de campo se
puede ver en el Tomo 1 de la nueva
edición del Manual de Cimentaciones
Profundas publicado por la SMIG y por
el M.I. Walter Paniagua y
colaboradores del Instituto de
Ingeniería de la UNAM.

58. Capacidad de Carga de
Cimentaciones Compensadas

59. Cimentaciones Compensadas
Tres casos de cimentaciones compensadas:
• Cimentación totalmente compensada
La carga de la estructura igual al peso del suelo excavado.
• Cimentación sobrecompensada
La carga de la estructura es menor al peso del suelo excavado.
• Cimentación subcompensada o parcialmente compensada
La carga de la estructura es mayor al peso del suelo excavado.

60. Cimentaciones Compensadas
Se debe considerar el estado de presiones en el suelo antes y
después de la construcción de la cimentación. El incremento
neto de presión Δ𝑤 vale:
Δ𝑤 = 𝑤𝑎 × 𝑤𝑜 − 𝑃𝑜𝑣
Dónde:
𝑤𝑎 Incremento neto de presión
𝑤𝑜 Incremento total de carga de toda la estructura
𝑃𝑜𝑣 Presión total inicial en el suelo a nivel de desplante

61. Capacidad de Carga de Pilotes

62. Una pausa: Terminología
Los términos pila y pilote no deben de ser intercambiables, pero
dependiendo de la normativa, manual o especificación pueden
significar lo mismo.
Para esta presentación un pilote es un elemento que es hincado
en el terreno por medios mecánicos o vibratorios y por lo mismo
no tiene geometrías grandes (< 60 cm).
Una pila es un elemento de diámetro mayor a 60 cm y es
perforado y colado en sitio.

63. Ecuación de Hincado
Una de las formas más comunes de calcular la capacidad de carga en
pilotes hincados es la ecuación de energía:
𝑅𝑢𝑑 =
𝑒𝑊ℎ
𝑠 +
𝑐
2
Dónde:
𝑅𝑢𝑑 Capacidad de carga última en la pila al momento del hincado
𝑒 Eficiencia del sistema de hincado
𝑊 Peso del martillo
ℎ Altura de caída del martillo
𝑠 Movimiento de desplazamiento del pilote después del golpe
𝑐 Rebote elástico de la pila (5 mm)
(Briaud, 2013)

64. Algunos datos de martillos diésel
(SMIG, 2001)

65. Capacidad de Carga en Rocas
Cimentaciones Superficiales
Cimentaciones Profundas

66. Capacidad de Carga en Rocas – Cimentaciones Superficiales
El diseño de cimentaciones superficiales suele utilizar la
resistencia a la compresión simple de la sustancia de la roca.
La sustancia de la roca es solo uno de los parámetros que
definen la resistencia de la roca, se debería de tomar en
cuenta la presencia de fracturas o juntas.
Es por eso que una de las formas de calcular la capacidad de
carga de una cimentación es por medio de su calidad de la roca.

67. Capacidad de Carga en Rocas – Cimentaciones Superficiales
RQD (%) Calidad de la Roca
Presión Admisible
(MPa)
100 Excelente 290
90 Buena 19
75 Regular 12
50 Pobre 6
25 Muy pobre 3
0 Similar al suelo 1
Se recomienda determinar el RQD de la roca a una profundidad igual al ancho de la cimentación.
VALORES DE CAPACIDAD DE CARGA SUGERIDOS EN ROCA (PECK ET. AL., 1974)

68. Capacidad de Carga en Rocas – Cimentaciones Profundas
El diseño de cimentaciones profundas suele utilizar la resistencia
a la compresión simple de la sustancia de la roca.
Aunque se suele recomendar que la cimentación quede
empotrada en la roca, con 1 o 2 diámetros de profundidad, en
la realidad esto es poco seguido debido a la dificultad de
perforación. Usualmente solo se perfora la roca alterada por
la meteorización ya que es más fácil.
Esto es útil para cargas axiales pero no para cargas
laterales.

69. Capacidad de Carga en Rocas – Cimentaciones Profundas
Por lo general se asume que la capacidad ultima se desarrolla a
una deformación vertical equivalente al 5% del diámetro de la
pila.
La capacidad ultima se calcula como 2.5xUCS, donde UCS es la
resistencia a la compresión simple de la sustancia de la roca
(AASHTO LRFD Bridge Design Manual, Section 10)
En muchísimos casos lo que termina controlando es
realmente la capacidad del concreto.
(Conversación con Sebastián Lobo-Guerrero)

70. Referencias
Das, B. M. (2010) Fundamentos de Ingeniería de Cimentaciones, 7ma
Edición, Cengage Learning.
Acevedo R., M. (2014) Teoría de Capacidad de Carga de Skempton
https://es.scribd.com/doc/213274611/Teoria-de-Skempton
SMIG (2001) Manual de Cimentaciones Profundas.
Briaud, J. L. (2013). Geotechnical engineering: unsaturated and saturated
soils. John Wiley & Sons.