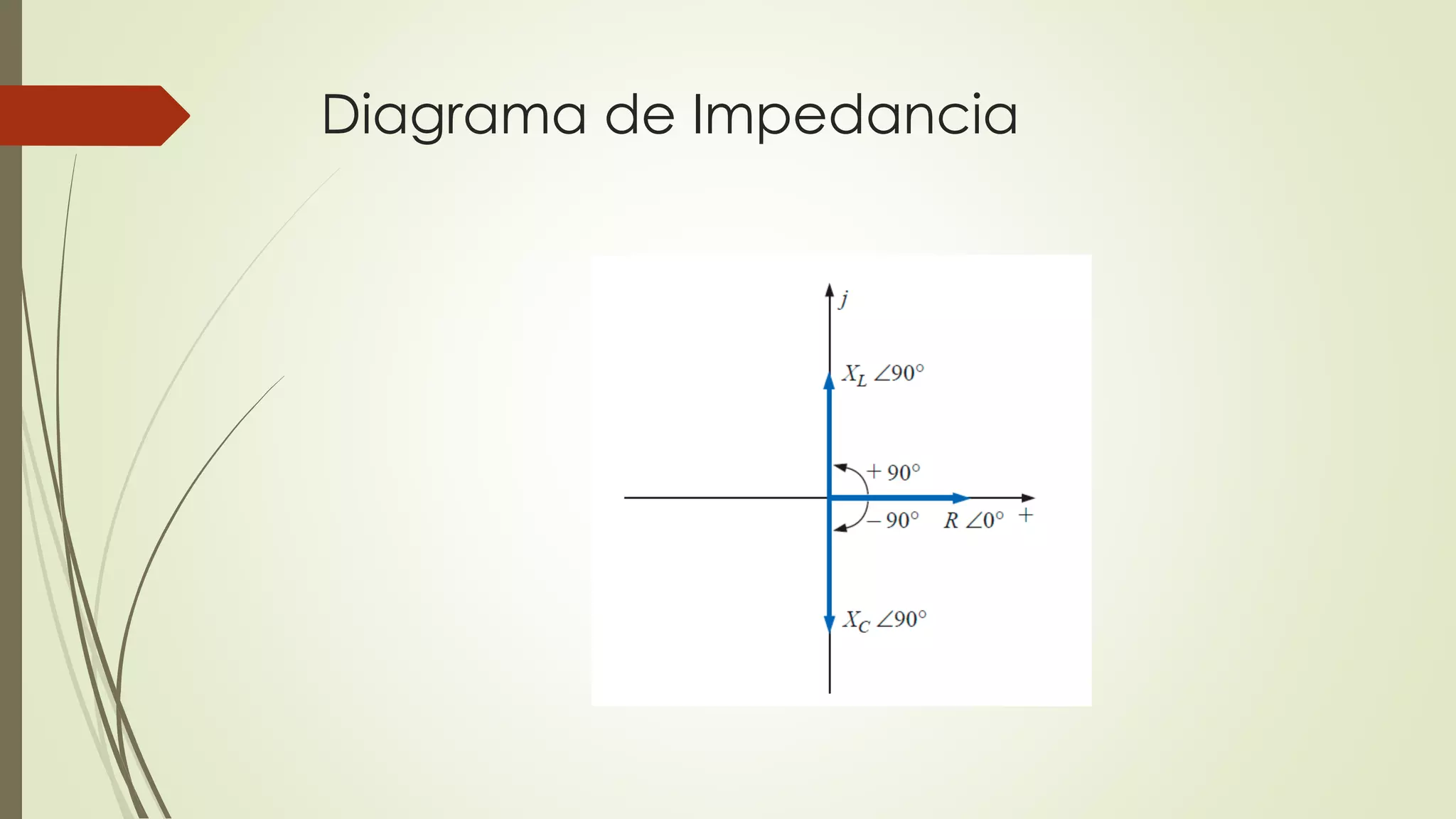
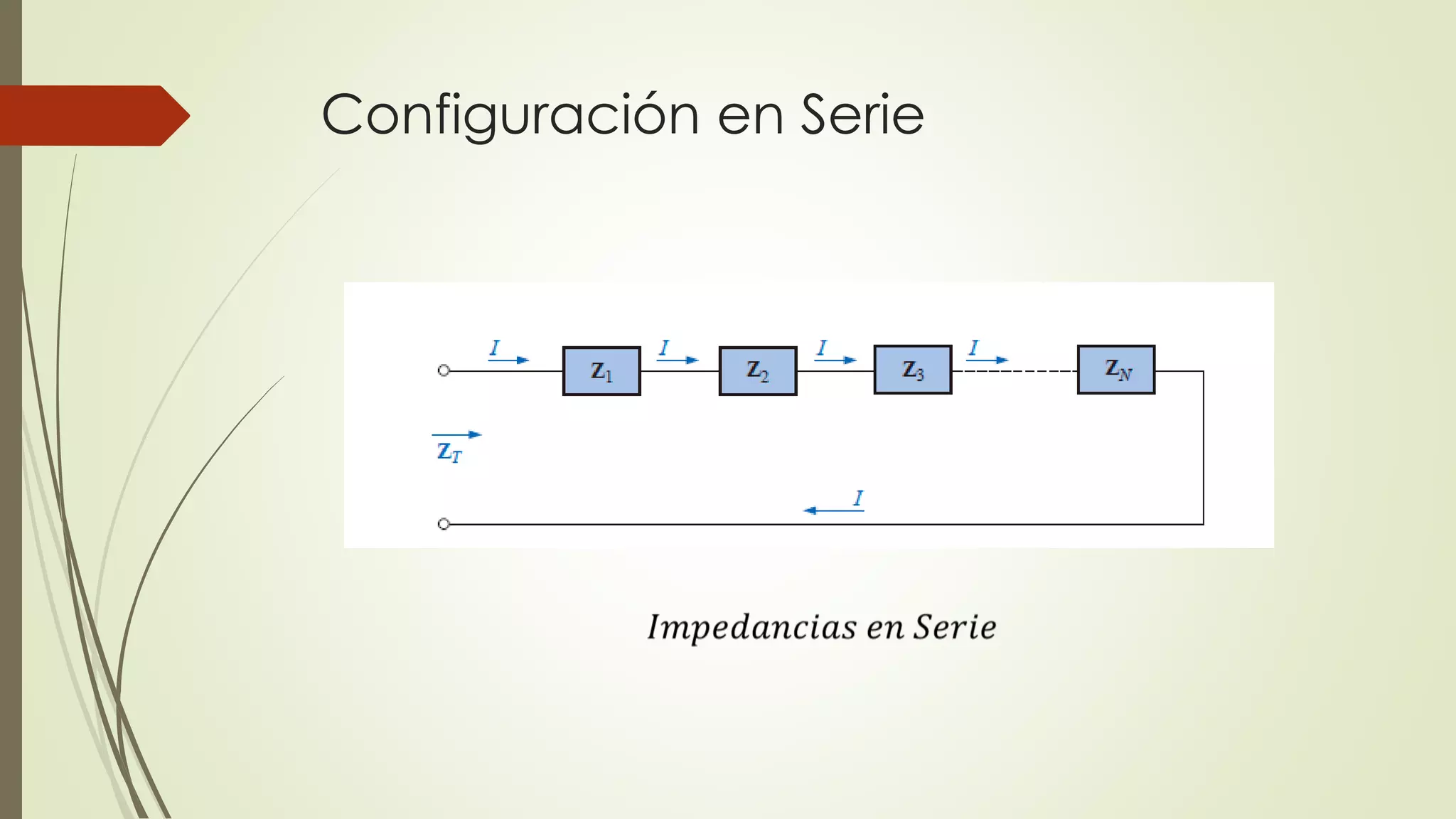
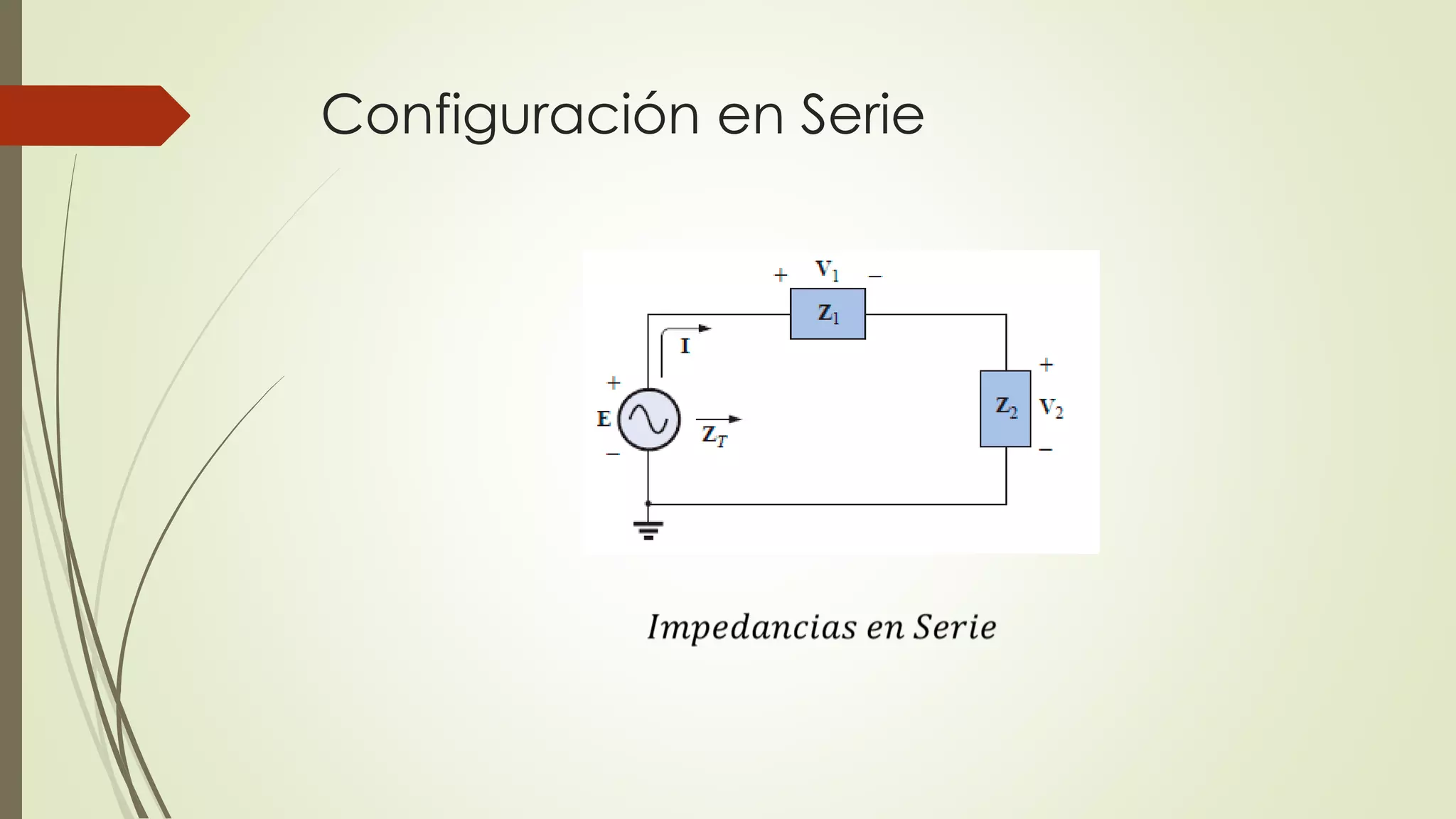
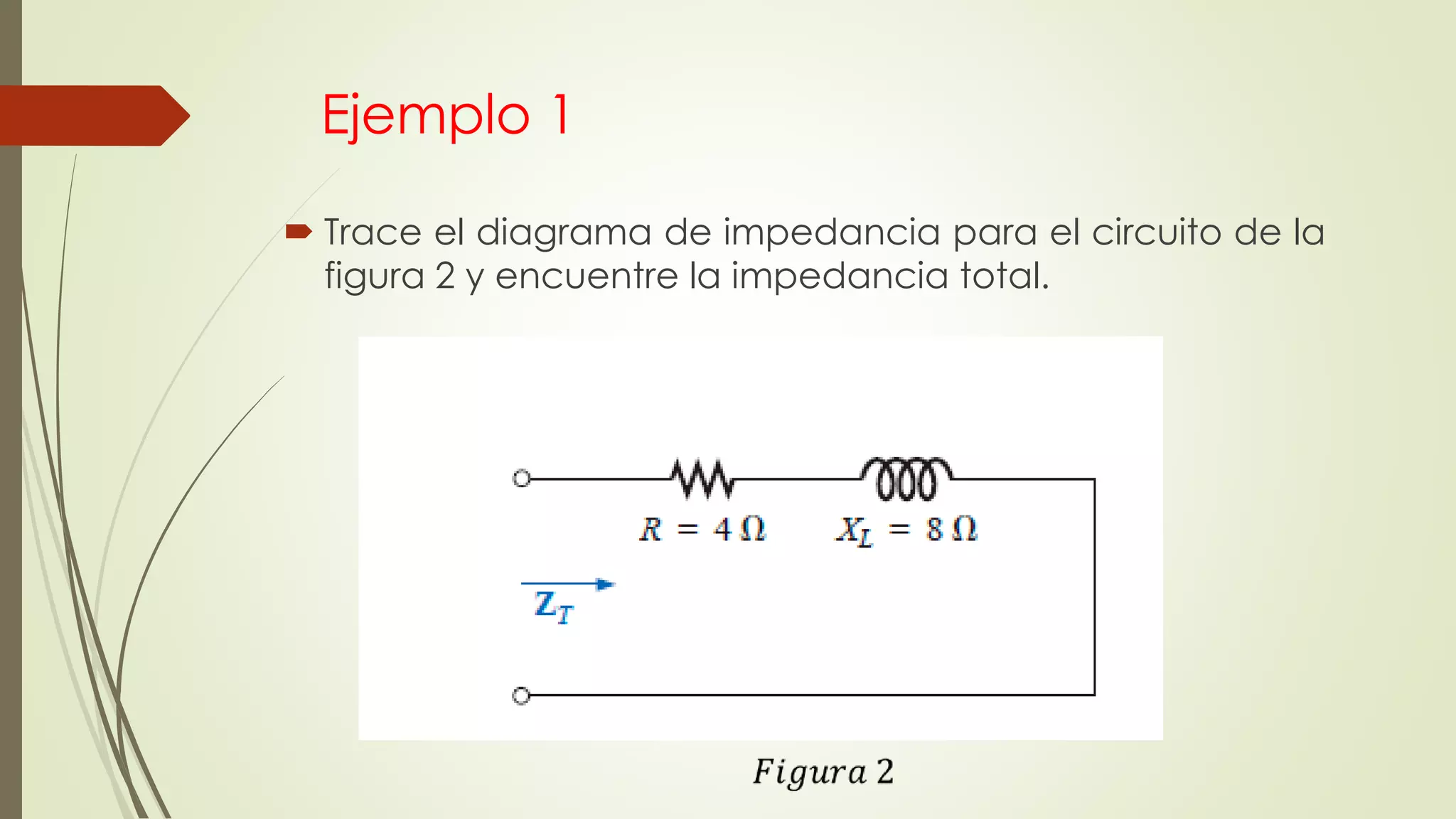
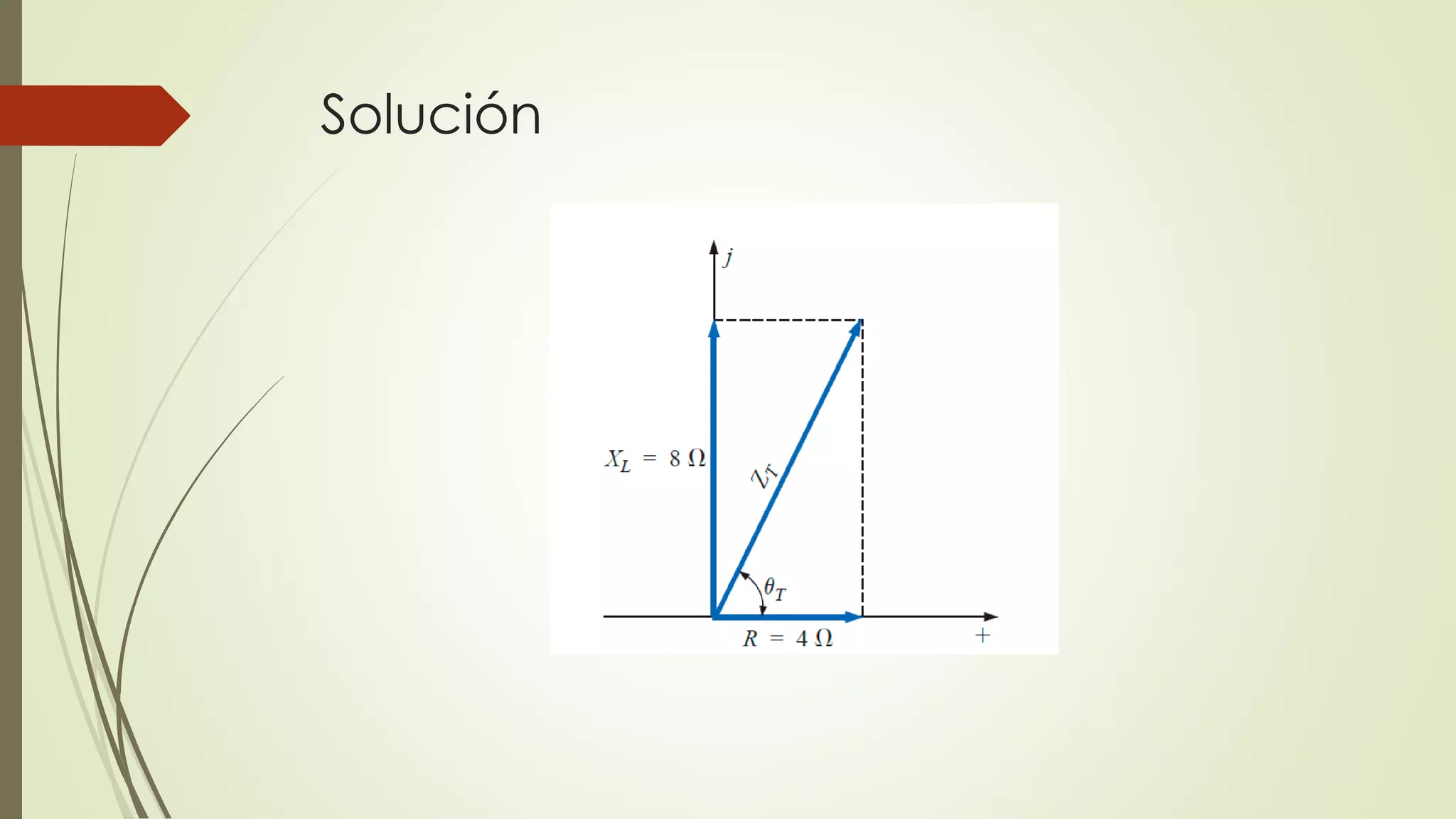
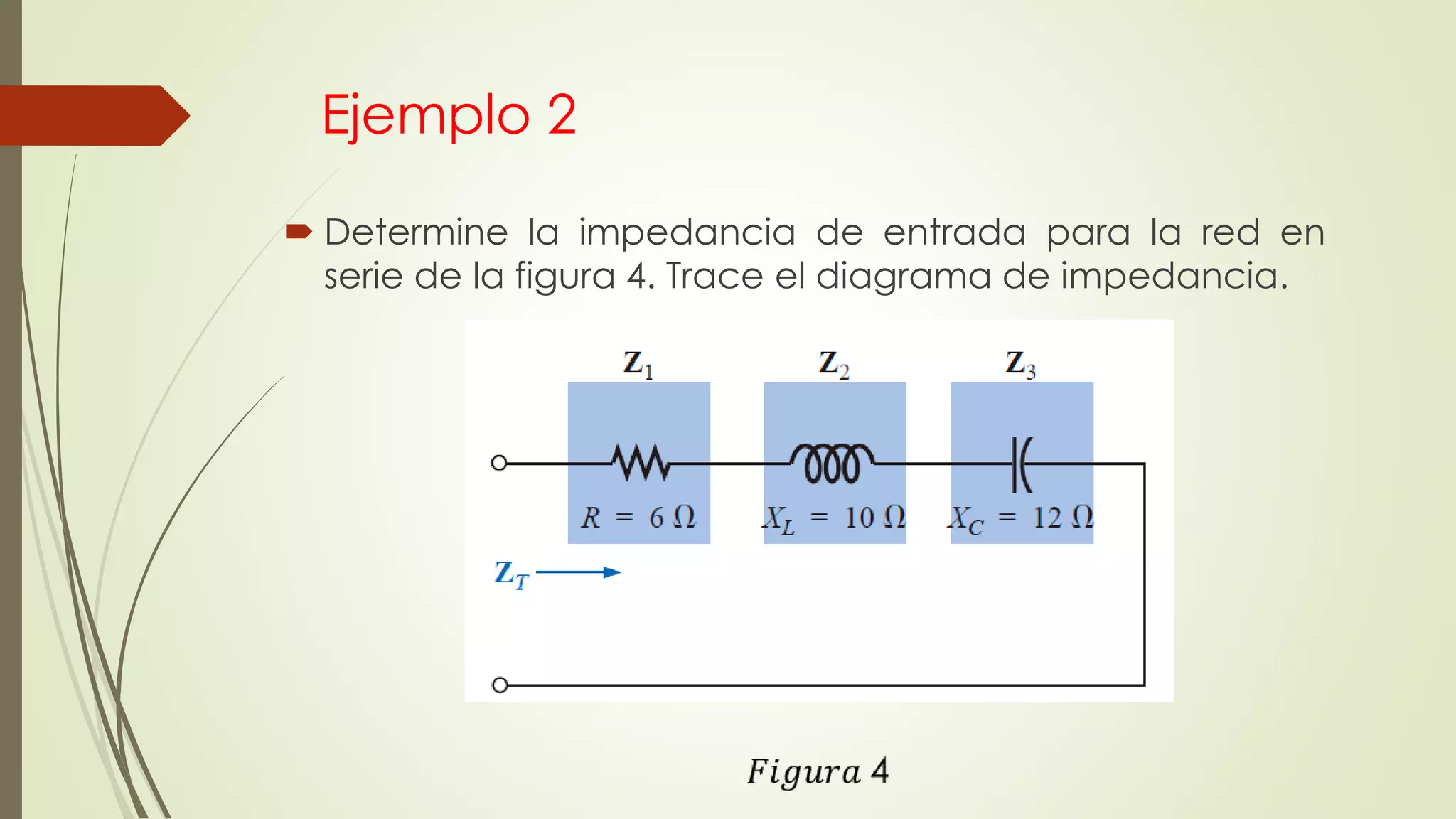
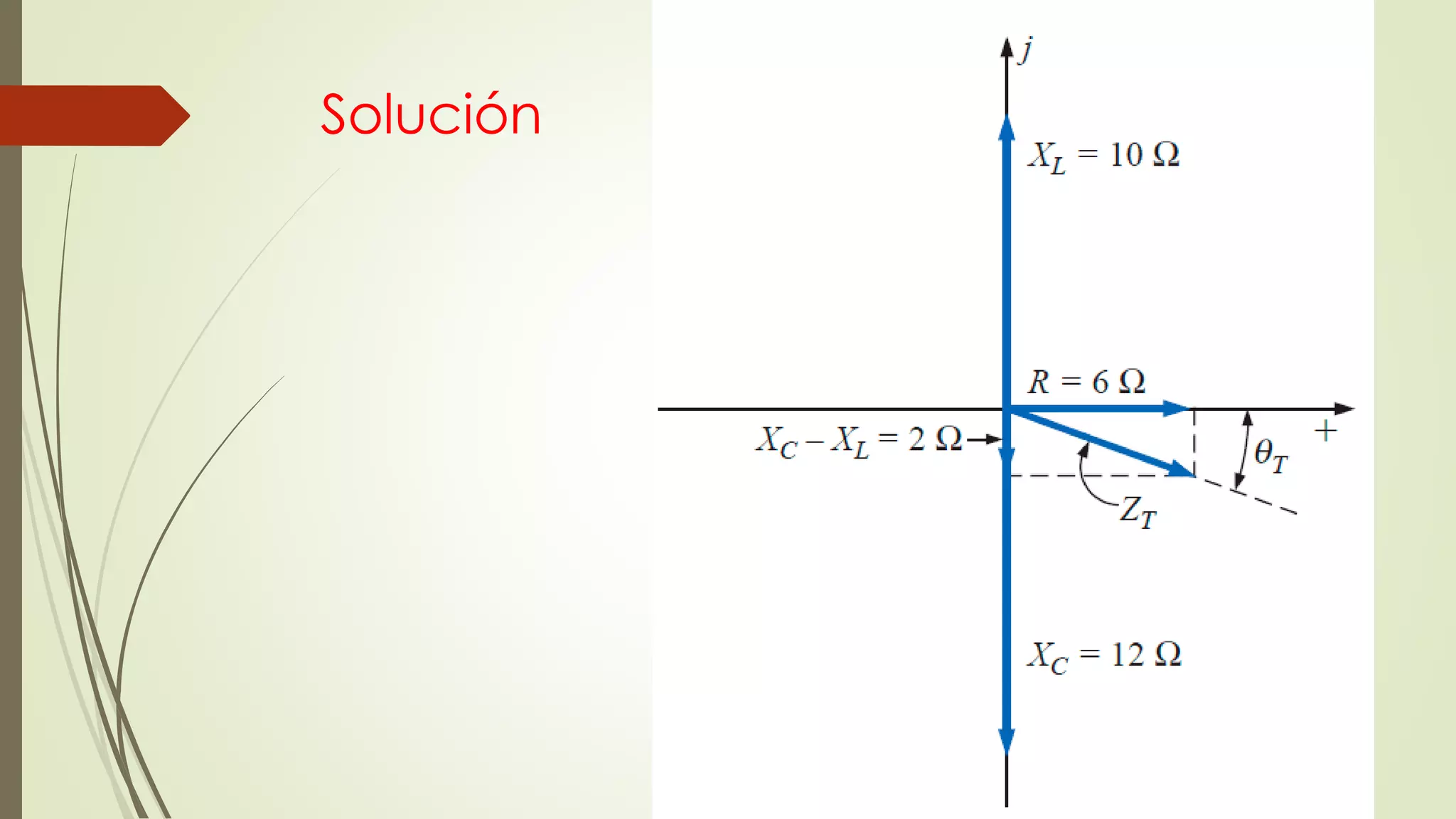
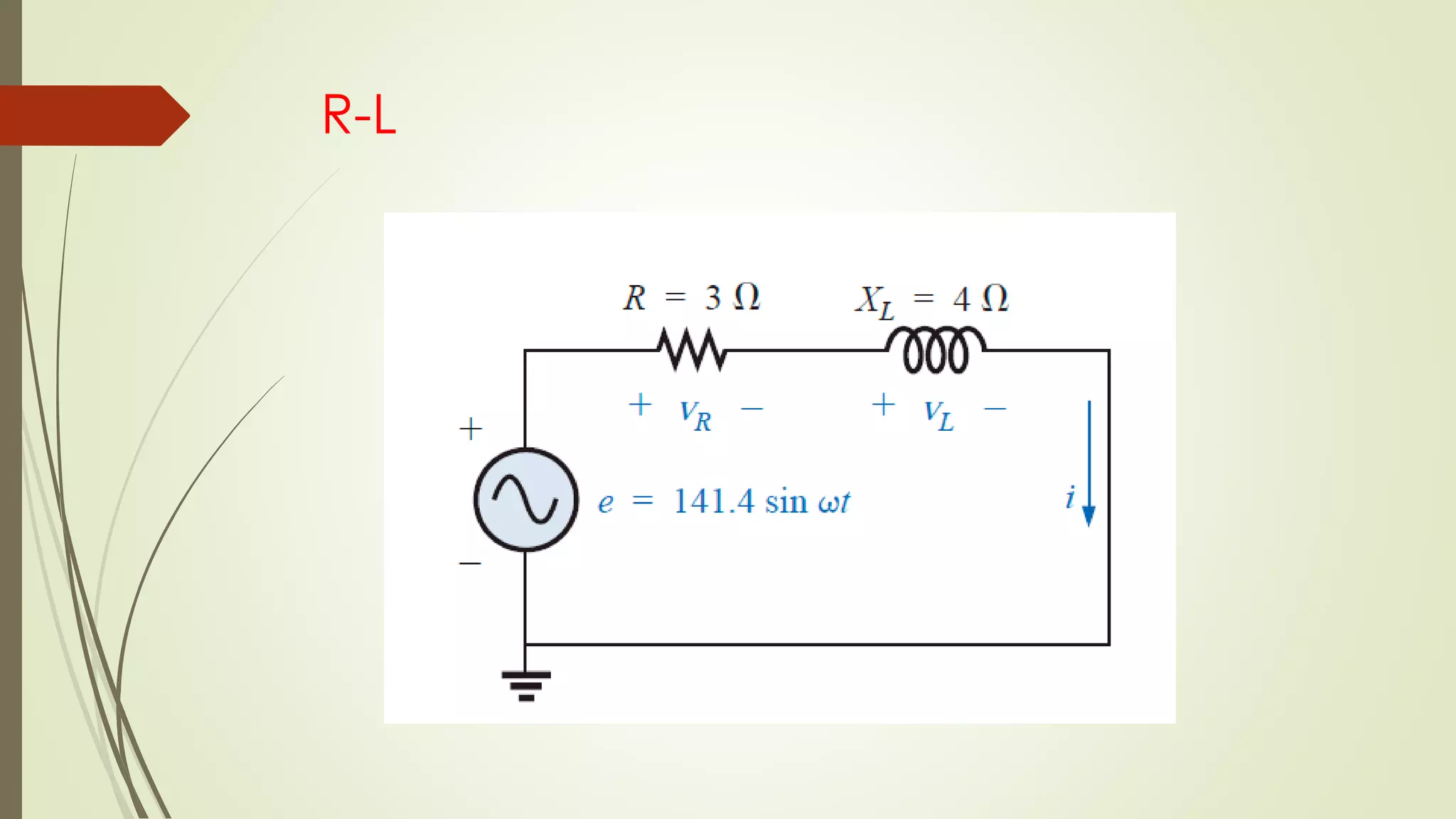
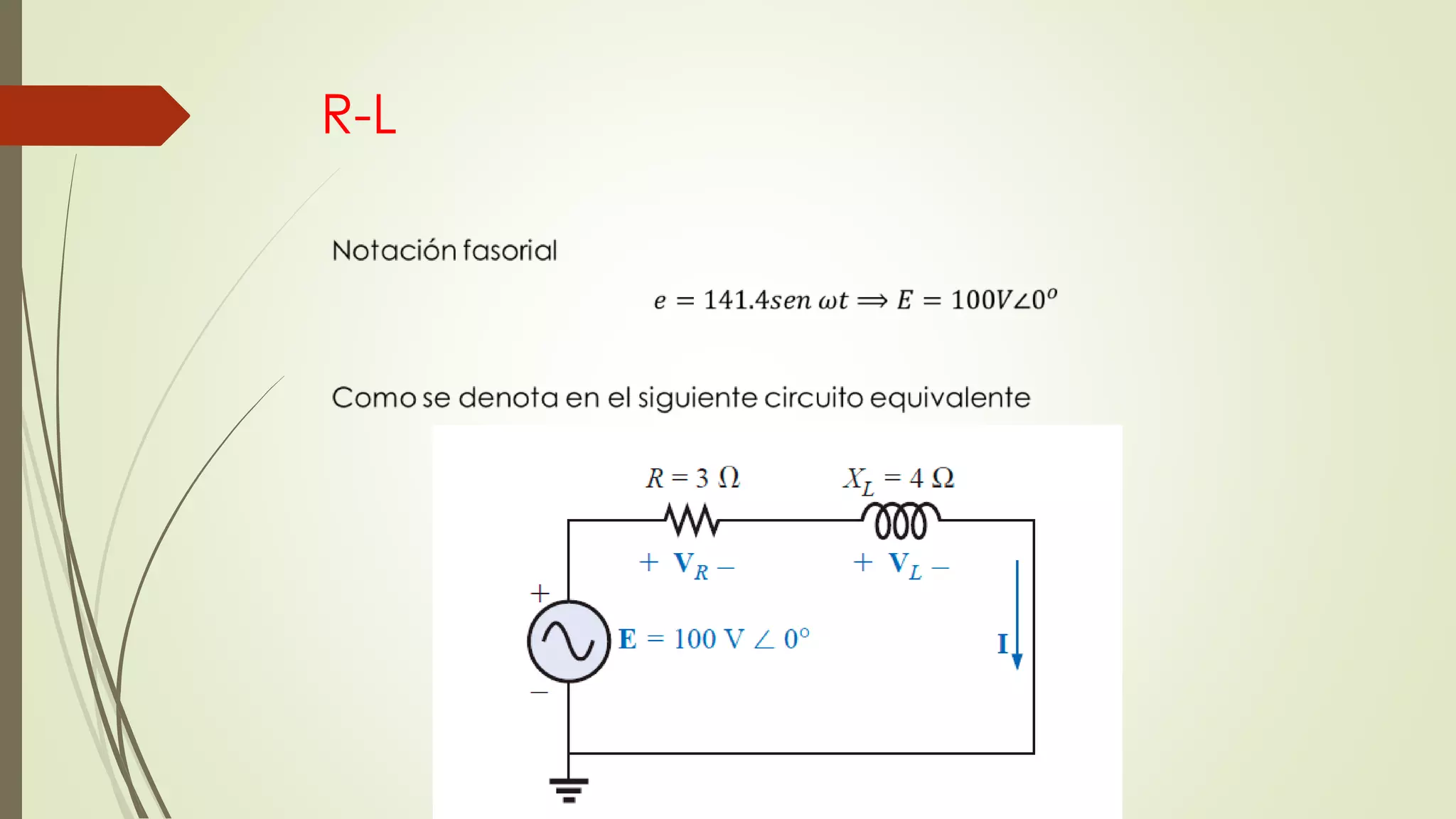
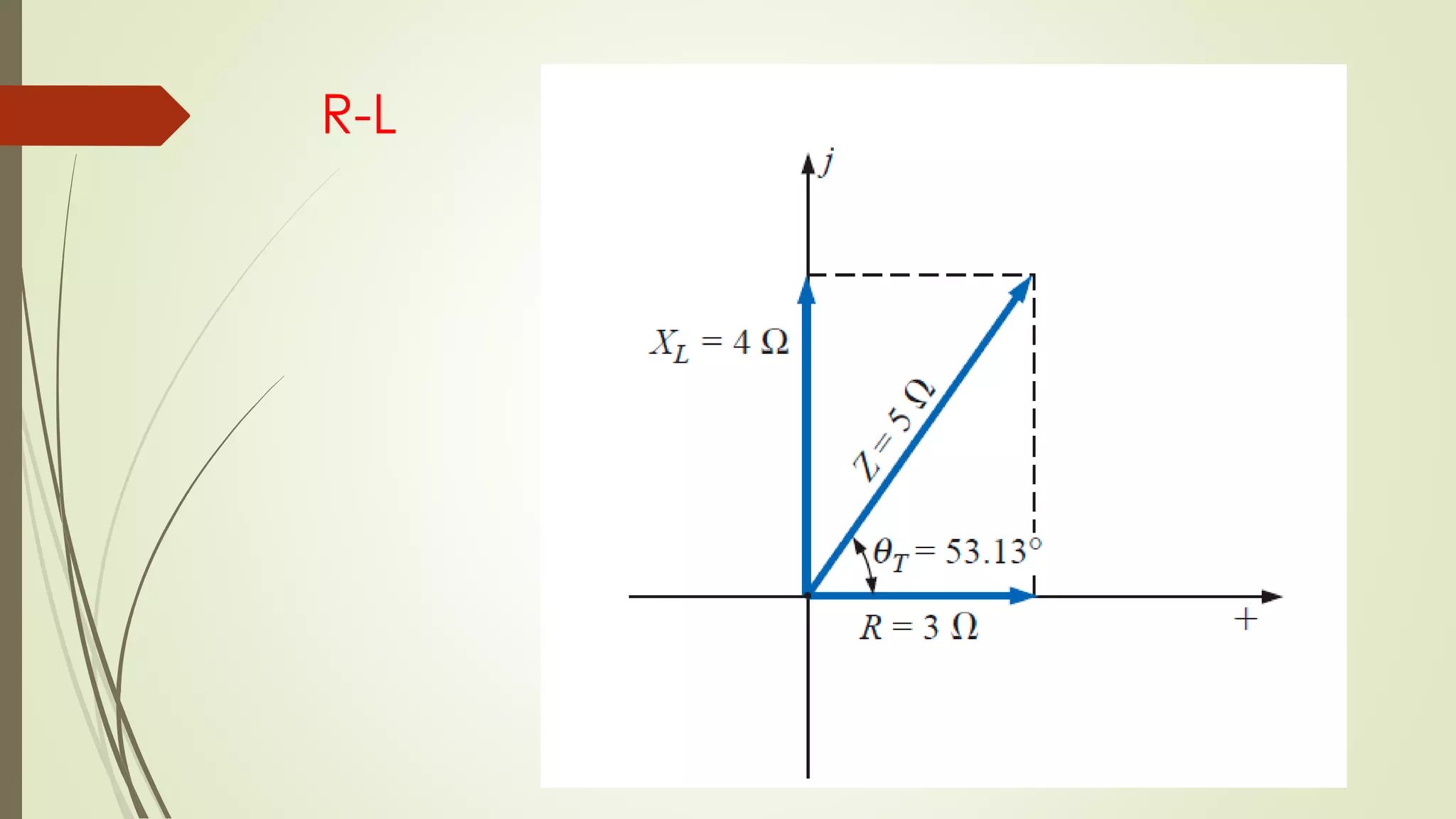
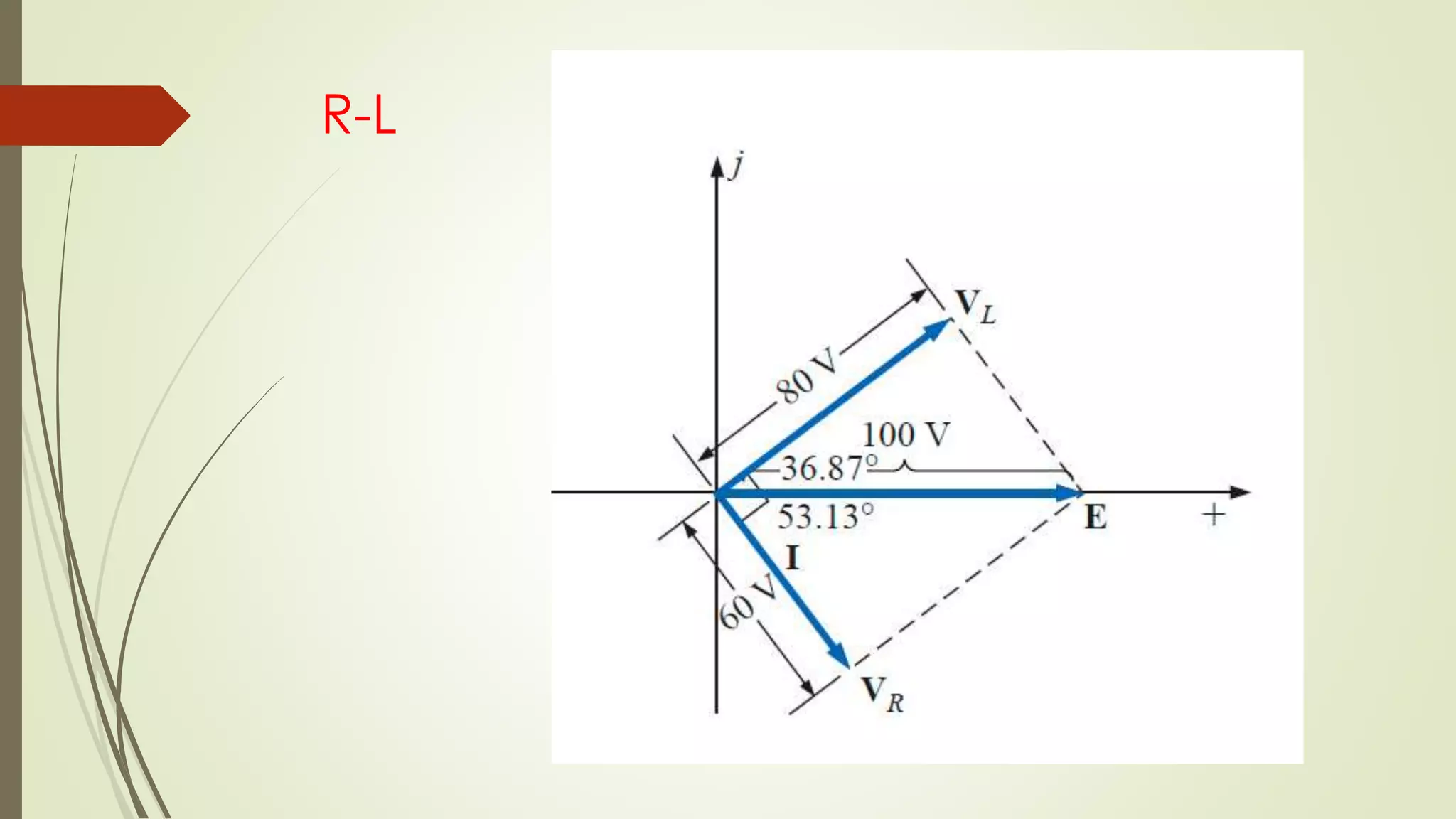
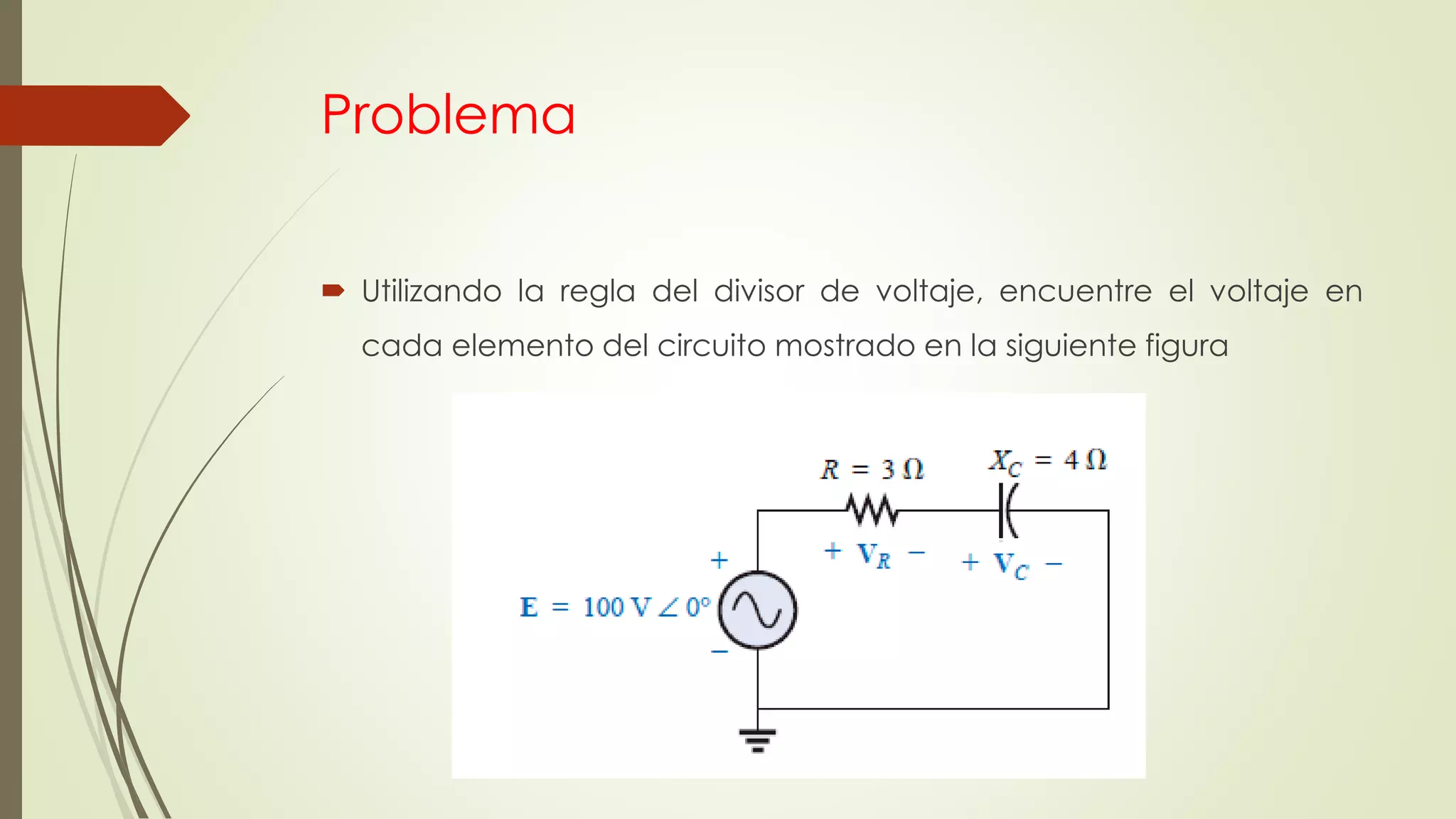
Este documento trata sobre circuitos en serie de corriente alterna. Explica que la impedancia total de un circuito en serie es la suma de las impedancias individuales, y cómo se pueden representar circuitos en serie usando diagramas de impedancia. También cubre conceptos como la ley de Ohm para corriente alterna y cómo calcular voltajes e impedancias totales en circuitos en serie.