Descargado 20 veces
Subido porTensor
Teoria de colas
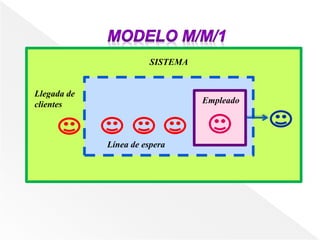
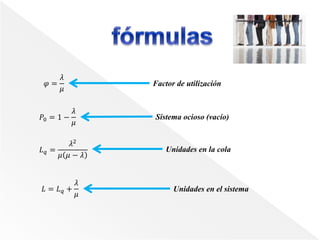
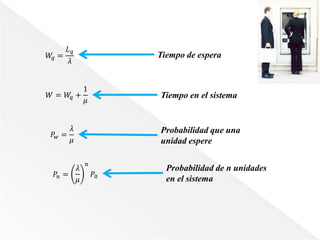
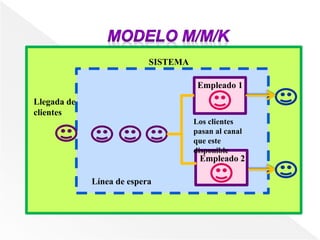
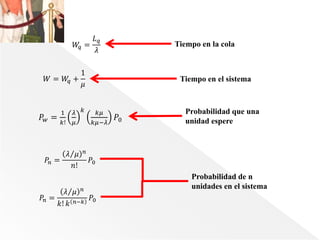
Este documento presenta las fórmulas y conceptos básicos de la teoría de colas para sistemas con un solo canal y múltiples canales. Para sistemas con un solo canal, introduce las fórmulas para calcular la probabilidad de que el sistema esté vacío, el número promedio de unidades en la cola y en el sistema, los tiempos promedio de espera y en el sistema. Para sistemas con múltiples canales, extiende estas fórmulas para cuando hay k canales en paralelo.
Más contenido relacionado
Teoria de colas
- 1.
- 2. Empleado Línea de espera Llegadade clientes SISTEMA
- 3. 𝑃0 = 1− 𝜆 𝜇 𝐿 𝑞 = 𝜆2 𝜇 𝜇 − 𝜆 𝐿 = 𝐿 𝑞 + 𝜆 𝜇 𝜑 = 𝜆 𝜇 Factor de utilización Unidades en el sistema Unidades en la cola Sistema ocioso (vacío)
- 4. 𝑊𝑞 = 𝐿 𝑞 𝜆 𝑊= 𝑊𝑞 + 1 𝜇 𝑃𝑤 = 𝜆 𝜇 𝑃𝑛 = 𝜆 𝜇 𝑛 𝑃0 Tiempo en el sistema Tiempo de espera Probabilidad que una unidad espere Probabilidad de n unidades en el sistema
- 5. Empleado 1 Línea deespera Llegada de clientes SISTEMA Empleado 2 Los clientes pasan al canal que este disponible
- 6. 𝑃0 = 1 𝑛=0 𝑘−1 (𝜆 𝜇) 𝑛 𝑛! + 𝜆 𝜇 𝑘 𝑘! 𝑘𝜇 𝑘𝜇 − 𝜆 𝐿 𝑞 = 𝜆 𝜇 2 𝑘 − 1 ! 𝑘𝜇 − 𝜆 2 𝜑 = 𝜆 𝑘𝜇 𝐿 = 𝐿 𝑞 + 𝜆 𝜇 Factor de utilización Unidades en el sistema Unidades en la cola Sistema ocioso (vacío)
- 7. 𝑃𝑤 = 1 𝑘! 𝜆 𝜇 𝑘 𝑘𝜇 𝑘𝜇−𝜆 𝑃0 𝑃𝑛= 𝜆 𝜇 𝑛 𝑛! 𝑃0 𝑃𝑛 = 𝜆 𝜇 𝑛 𝑘! 𝑘 𝑛−𝑘 𝑃0 𝑊𝑞 = 𝐿 𝑞 𝜆 𝑊 = 𝑊𝑞 + 1 𝜇 Tiempo en la cola Tiempo en el sistema Probabilidad que una unidad espere Probabilidad de n unidades en el sistema