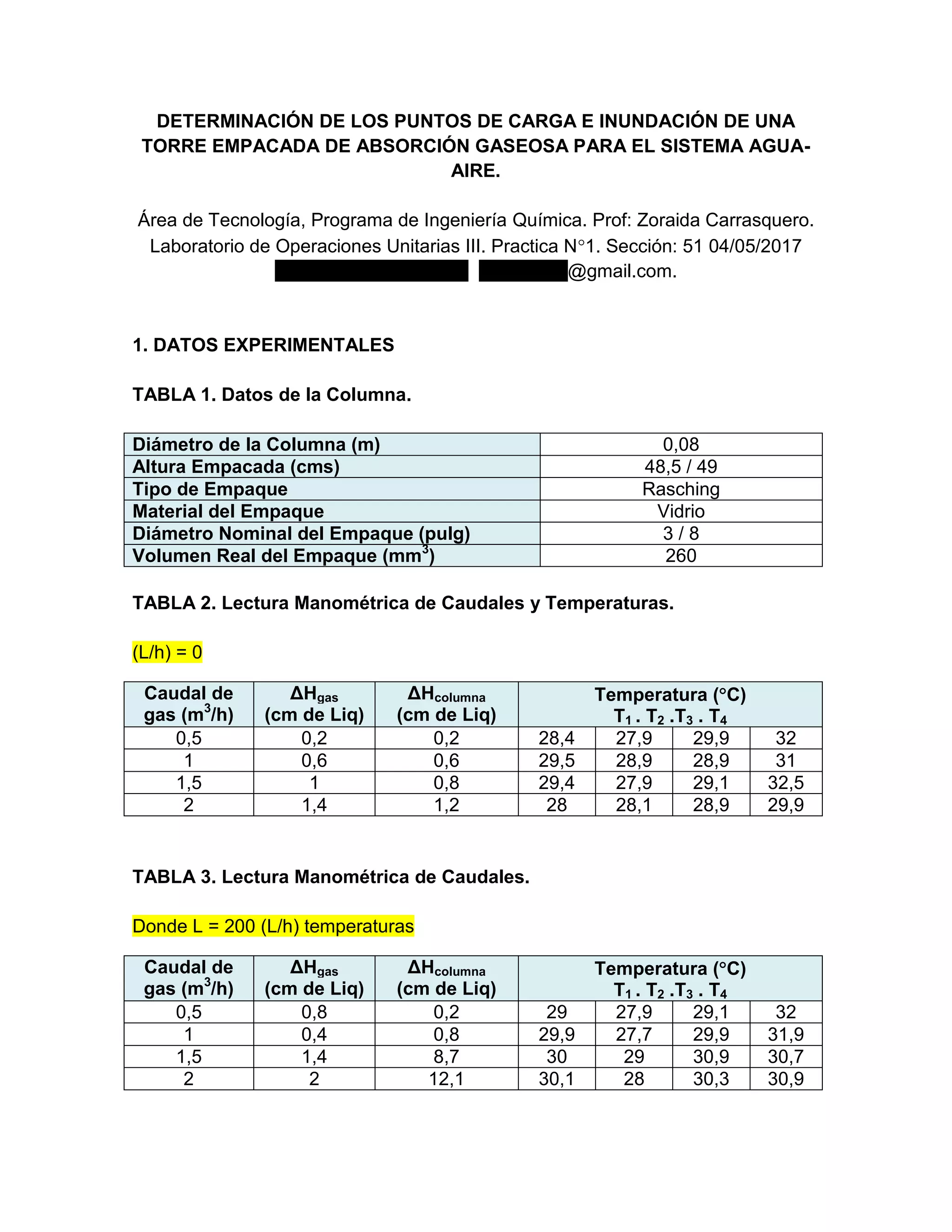
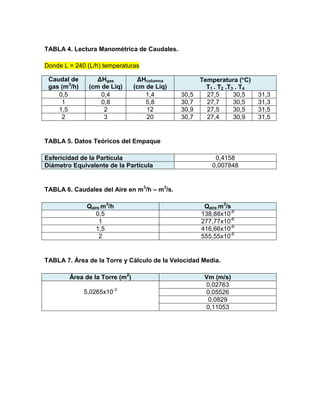
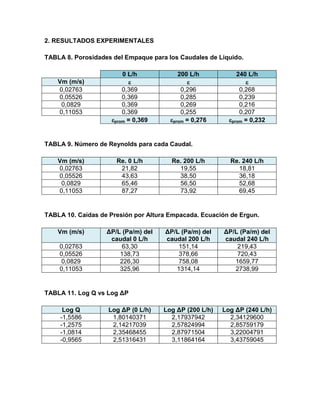
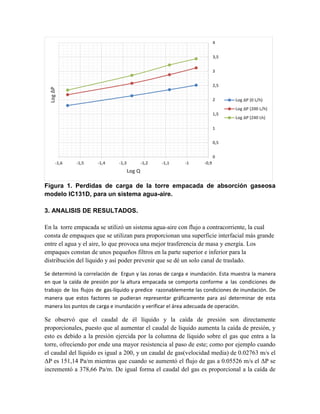
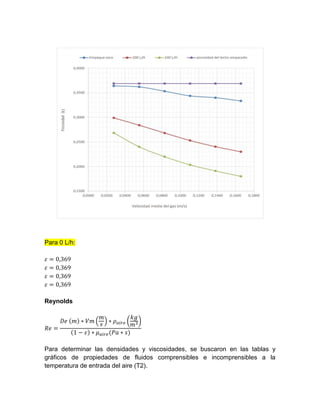
El documento detalla un experimento sobre la determinación de puntos de carga e inundación de una torre empacada utilizada en un sistema agua-aire, incluyendo datos experimentales y teóricos. Se constató que la caída de presión es directamente proporcional al caudal del gas y líquido, influyendo en la eficiencia de la transferencia de masa. Las conclusiones subrayan la importancia de la relación entre caudales, caída de presión y condiciones de inundación en la operación de la torre.

1. DETERMINACIÓN DE LOS PUNTOS DE CARGA E INUNDACIÓN DE UNA
TORRE EMPACADA DE ABSORCIÓN GASEOSA PARA EL SISTEMA AGUA-
AIRE.
Área de Tecnología, Programa de Ingeniería Química. Prof: Zoraida Carrasquero.
Laboratorio de Operaciones Unitarias III. Practica N1. Sección: 51 04/05/2017
fabioladiaz@gmail.com EdgarOrtiz@gmail.com.
1. DATOS EXPERIMENTALES
TABLA 1. Datos de la Columna.
Diámetro de la Columna (m) 0,08
Altura Empacada (cms) 48,5 / 49
Tipo de Empaque Rasching
Material del Empaque Vidrio
Diámetro Nominal del Empaque (pulg) 3 / 8
Volumen Real del Empaque (mm3
) 260
TABLA 2. Lectura Manométrica de Caudales y Temperaturas.
(L/h) = 0
Caudal de
gas (m3
/h)
ΔHgas
(cm de Liq)
ΔHcolumna
(cm de Liq)
Temperatura (C)
T1 . T2 .T3 . T4
0,5 0,2 0,2 28,4 27,9 29,9 32
1 0,6 0,6 29,5 28,9 28,9 31
1,5 1 0,8 29,4 27,9 29,1 32,5
2 1,4 1,2 28 28,1 28,9 29,9
TABLA 3. Lectura Manométrica de Caudales.
Donde L = 200 (L/h) temperaturas
Caudal de
gas (m3
/h)
ΔHgas
(cm de Liq)
ΔHcolumna
(cm de Liq)
Temperatura (C)
T1 . T2 .T3 . T4
0,5 0,8 0,2 29 27,9 29,1 32
1 0,4 0,8 29,9 27,7 29,9 31,9
1,5 1,4 8,7 30 29 30,9 30,7
2 2 12,1 30,1 28 30,3 30,9

2. TABLA 4. Lectura Manométrica de Caudales.
Donde L = 240 (L/h) temperaturas
Caudal de
gas (m3
/h)
ΔHgas
(cm de Liq)
ΔHcolumna
(cm de Liq)
Temperatura (C)
T1 . T2 .T3 . T4
0,5 0,4 1,4 30,5 27,5 30,5 31,3
1 0,8 5,8 30,7 27,7 30,5 31,3
1,5 2 12 30,9 27,5 30,5 31,5
2 3 20 30,7 27,4 30,9 31,5
TABLA 5. Datos Teóricos del Empaque
Esfericidad de la Partícula 0,4158
Diámetro Equivalente de la Partícula 0,007848
TABLA 6. Caudales del Aire en m3
/h – m3
/s.
Qaire m3
/h Qaire m3
/s
0,5 138,88x10-6
1 277,77x10-6
1,5 416,66x10-6
2 555,55x10-6
TABLA 7. Área de la Torre y Cálculo de la Velocidad Media.
Área de la Torre (m2
) Vm (m/s)
5,0265x10-3
0,02763
0,05526
0,0829
0,11053

3. 2. RESULTADOS EXPERIMENTALES
TABLA 8. Porosidades del Empaque para los Caudales de Liquido.
0 L/h 200 L/h 240 L/h
Vm (m/s)   
0,02763 0,369 0,296 0,268
0,05526 0,369 0,285 0,239
0,0829 0,369 0,269 0,216
0,11053 0,369 0,255 0,207
prom = 0,369 prom = 0,276 prom = 0,232
TABLA 9. Número de Reynolds para cada Caudal.
Vm (m/s) Re. 0 L/h Re. 200 L/h Re. 240 L/h
0,02763 21,82 19,55 18,81
0,05526 43,63 38,50 36,18
0,0829 65,46 56,50 52,68
0,11053 87,27 73,92 69,45
TABLA 10. Caídas de Presión por Altura Empacada. Ecuación de Ergun.
Vm (m/s) ΔP/L (Pa/m) del
caudal 0 L/h
ΔP/L (Pa/m) del
caudal 200 L/h
ΔP/L (Pa/m) del
caudal 240 L/h
0,02763 63,30 151,14 219,43
0,05526 138,73 378,66 720,43
0,0829 226,30 758,08 1659,77
0,11053 325,96 1314,14 2738,99
TABLA 11. Log Q vs Log ΔP
Log Q Log ΔP (0 L/h) Log ΔP (200 L/h) Log ΔP (240 L/h)
-1,5586 1,80140371 2,17937942 2,34129600
-1,2575 2,14217039 2,57824994 2,85759179
-1,0814 2,35468455 2,87971504 3,22004791
-0,9565 2,51316431 3,11864164 3,43759045

4. Figura 1. Perdidas de carga de la torre empacada de absorción gaseosa
modelo IC131D, para un sistema agua-aire.
3. ANALISIS DE RESULTADOS.
En la torre empacada se utilizó un sistema agua-aire con flujo a contracorriente, la cual
consta de empaques que se utilizan para proporcionan una superficie interfacial más grande
entre el agua y el aire, lo que provoca una mejor trasferencia de masa y energía. Los
empaques constan de unos pequeños filtros en la parte superior e inferior para la
distribución del líquido y así poder prevenir que se dé un solo canal de traslado.
Se determinó la correlación de Ergun y las zonas de carga e inundación. Esta muestra la manera
en que la caída de presión por la altura empacada se comporta conforme a las condiciones de
trabajo de los flujos de gas-líquido y predice razonablemente las condiciones de inundación. De
manera que estos factores se pudieran representar gráficamente para así determinar de esta
manera los puntos de carga e inundación y verificar el área adecuada de operación.
Se observó que el caudal de él líquido y la caída de presión son directamente
proporcionales, puesto que al aumentar el caudal de líquido aumenta la caída de presión, y
esto es debido a la presión ejercida por la columna de líquido sobre el gas que entra a la
torre, ofreciendo por ende una mayor resistencia al paso de este; como por ejemplo cuando
el caudal del líquido es igual a 200, y un caudal de gas(velocidad media) de 0.02763 m/s el
ΔP es 151,14 Pa/m mientras que cuando se aumentó el flujo de gas a 0.05526 m/s el ΔP se
incrementó a 378,66 Pa/m. De igual forma el caudal del gas es proporcional a la caída de
0
0,5
1
1,5
2
2,5
3
3,5
4
-1,6 -1,5 -1,4 -1,3 -1,2 -1,1 -1 -0,9
LogΔP
Log Q
Log ΔP (0 L/h)
Log ΔP (200 L/h)
Log ΔP (240 Lh)

5. presión debido a que al incrementar el caudal de aire, se ve incrementada su velocidad y a
su vez la fricción por los empaques con el paso del aire a través de ellos.
4. CONCLUSIONES
 La Caída de Presión es directamente proporcional al Caudal y Velocidad
del Gas.
 A través de la Ecuación de Leva se puede determinar en las torres
empacadas las pérdidas de carga, caídas de presión en función de la altura
y los casos de inundación que pueden ocurrir en la misma.
 Cuando se trabaja con empaques secos no se puede determinar el Punto
de Carga ni Inundación, ya que este arroja una línea recta.
 A mayor cantidad de caudal, se estima que se reduce el porcentaje de error
y se obtendrían mejores beneficios.
 A mayor área de contacto interfacial, mayor será la transferencia de masa.
 En la región comprendida entre el punto de carga y el punto inundación, la
retención de líquido aumenta rápidamente con el flujo del gas, mientras que
el área libre para el flujo de gas se reduce y la presión en la torre aumenta,
esto debido a que la fase liquida se vuelve turbulenta.
 El Punto de Inundación de la Torre se observa de manera experimental
cuando se forman burbujas en la parte superior de los empaques dentro de
la misma.
 Se recomienda que una misma persona realice las lecturas en los
manómetros para tener el mismo margen de error.
5. REFERENCIAS BIBLIOGRAFICAS
 McCabe. W, Smith. J, Harriott. P. Operaciones Unitarias en Ingeniería
Química. Mc Graw Hill. Séptima Edición. Capítulo 18.
 Perry. R, Green. D, Manual del Ingeniero Químico. Mc Graw Hill. Séptima
Edición. Volumen I. Capítulo 1.

6.  Perry. R, Green. D, Manual del Ingeniero Químico. Mc Graw Hill. Séptima
Edición. Volumen III. Capítulo 14.
 UNEFM. Manual de Laboratorio de Operaciones Unitarias III. Corte III-2012.
Practica Nº 1.
6. APENDICE
Para L = 0 L/h
Transformar los valores para Q, medidos en m3
/h a m3
/s con el caudal del aire,
Qaire = 0,5 m3
/h y los otros caudales.
Área de la Torre
NOTA: El valor del diámetro de la torre (D) es un valor suministrado.
Velocidad Media
Porosidad
Para el cálculo de la porosidad se utilizo la Grafica N3 del comportamiento de la
porosidad experimental en función de la velocidad media del gas a empaque seco
y flujos de líquido.

7. Para 0 L/h:
Reynolds
( ) ( )
Para determinar las densidades y viscosidades, se buscaron en las tablas y
gráficos de propiedades de fluidos comprensibles e incomprensibles a la
temperatura de entrada del aire (T2).

8. NOTA: El diámetro equivalente (De) es un valor suministrado.
( ) ( )
Determinación de la caída de presión por altura empacada utilizando la
ecuación de Ergun
( ) ( ) ( )
=
= 63,30 Pa/m