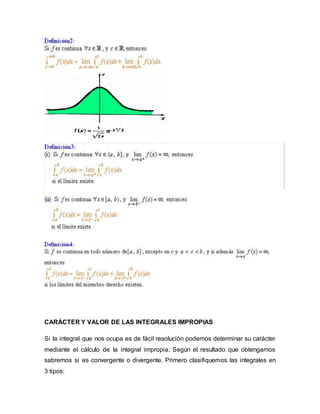
Este documento define las integrales impropias y explica que ocurren cuando el intervalo de integración o la función no son bien comportados. Explica que hay diferentes tipos de integrales impropias dependiendo de si la función se hace infinita en los límites o en puntos internos. Finalmente, detalla cómo determinar si una integral impropia convergente o divergente dependiendo de si las integrales de primera y segunda especie que la componen son convergentes o no.

1. Universidad “Fermín Toro”
Vice-Rectorado Académico
Facultad de Relaciones Industriales
Núcleo Araure- Portuguesa
Participante:
Meiker, Martinez
C.I. 24895665
Matemática II
SAIA
Araure, abril 2016

2. DEFINICIÓN DE INTEGRALES IMPROPIAS
Las denominadas integrales impropias son una clase especial de integrales
definidas (integrales de Riemann) en las que el intervalo de integración o
la función en el integrando o ambos presentan ciertas particularidades. Las
integrales impropias no son realmente una nueva forma de integrales, sino una
extensión natural a las propiedades de la integral y un replanteamiento de
nuestro concepto de área bajo la curva.
es impropia si se presenta uno de los siguientes casos:
1.- a = - o b = a = - y b =
2.- no es acotada en alguno de los puntos de dichos puntos se llaman
singularidades de
Existes diversos tipos de integrales impropias las cuales definiremos a
continuación:

3. CARÁCTER Y VALOR DE LAS INTEGRALES IMPROPIAS
Si la integral que nos ocupa es de fácil resolución podemos determinar su carácter
mediante el cálculo de la integral impropia. Según el resultado que obtengamos
sabremos si es convergente o divergente. Primero clasifiquemos las integrales en
3 tipos:

4.  Primera especie
Son del tipo:
ó
Presentan una asíntota horizontal.
 Segunda especie
Son del tipo:
y que no está definida en el intervalo de integración o en cualquier
punto del dominio o los extremos de integración.
Presentan una asíntota vertical.
 Tercera especie
Son mezclas de los dos tipos anteriores, es decir, que presentan un infinito en
los extremos de integración y la función se hace infinito en uno o más puntos del
intervalo de integración.
Este tipo de integrales impropias se pueden dividir en suma de dos integrales:
una de primera especie y otra de segunda especie. Por lo tanto deberemos seguir
los pasos anteriores para determinar su carácter, y tener en cuenta que para que
sea convergente tanto la integral de primera especie como la de segunda especie
tienen que ser convergentes, si no, en cualquier otro caso, diverge.

5. EJERCICIOS RESUELTOS
1)
2)

6. 3)

7. 4)