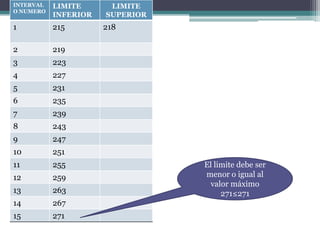
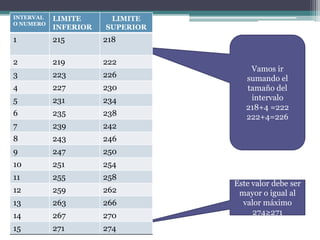
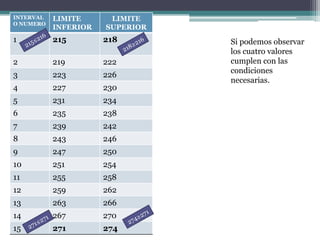
Este documento explica cómo calcular intervalos aparentes de datos agrupados. Primero, se encuentran el valor mínimo y máximo de los datos para determinar el rango. Luego, se elige un número de intervalos y se calcula el tamaño de cada intervalo dividiendo el rango entre el número de intervalos. Finalmente, se establecen los límites inferiores y superiores de cada intervalo sumando el tamaño de intervalo de forma secuencial.

1. Como obtener los
intervalos aparentes

2. INTRODUCCION
• En esta presentación que le muestro a
continuación , como obtener el calculo de
intervalos aparentes.
• El objetivo es mostrar detalladamente las
operaciones que se deben realizar para obtener
el resultado.

3. Datos Agrupados
232 240 230 256 233 266 245 239 245 240 239 247 258 251 260 245 233 244 241 246 261 259 237 242 220 249 255 232 245 244
247 248 249 254 235 242 249 248 254 248 239 246 242 242 225 243 243 230 243 235 245 250 250 248 240 245 239 246 241 246
232 235 253 249 235 254 216 247 241 258 244 247 245 231 255 251 239 239 263 235 262 246 257 247 244 255 248 244 231 248
236 229 254 246 235 242 240 250 241 263 263 249 242 248 230 258 254 257 247 250 253 271 250 234 263 251 255 256 248 253
246 260 258 234 260 239 238 241 257 244 254 251 217 243 264 245 253 238 240 241 250 247 247 242 250 250 244 246 248 237
257 229 255 247 257 245 245 249 254 256 237 249 252 244 252 232 240 249 258 251 232 245 241 241 246 242 240 251 242 236
249 233 237 256 246 245 258 240 257 254 251 254 248 248 243 252 243 258 253 242 249 229 261 246 244 245 239 234 258 257
225 237 250 248 239 226 253 243 233 256 242 242 238 246 250 243 242 232 261 242 258 243 249 248 241 258 247 255 255 258
245 248 249 227 240 246 244 241 251 254 252 253 252 258 240 250 234 245 239 246 247 245 249 264 244 239 253 260 243 239
252 254 251 244 240 247 244 248 238 240 260 244 242 244 266 237 249 246 237 235 236 240 247 253 241 245 246 252 235 228

4. DATOS AGRUPADOS
• PRIMER PASO
• 1. Encontrar el mínimo y máximo de la tabla de
datos
• Valor mínimo : 216
• Valor máximo: 271
• Rango : 271-216 = 55

5. SEGUNDO PASO
• Se determina el numero de intervalos en que se
van agrupar los datos.
• Establecemos arbitrariamente el numero de
intervalos con el cual vamos a realizar en este
caso seria de 15

6. TERCER PASO
• Determinamos el tamaño del intervalo,
• Este se determina diviendo el rango entre el
numero de intervalos:
En este caso como
estamos trabajando
• 55/15 = 3.6 con números
enteros, se puede
redondear a 4 para
poder obtener los
intervalos con
éxito, en algunos
casos es necesario
intentar varias veces

7. CUARTO PASO DETERMINAR
INTERVALOS APARENTES
• Se elige un valor inicial el cual este será el
primer limite inferior, este debe ser menor o
igual al valor mínimo, en este caso seria el
numero 215

8. INTERVALOS APARENTES
INTERVALO LIMITE LIMITE
NUMERO De este punto se parte
INFERIOR SUPERIOR
el valor inicial y se
1 215 calculan los 10
limites inferiores.
Se ira
2 NUMERO
ELEGIDO
sumando el Se va sumando a cada
3 , TAMBIEN tamaño del limite el tamaño de
PUDO intervalo Intervalo.
HABER SIDO 215+4
4
213,214
219+4
5
6
7
8
9
10

9. INTERVAL LIMITE LIMITE
O NUMERO
INFERIOR SUPERIOR
1 215 218
2 219
3 223
4 227
5 231
6 235
7 239
8 243
9 247
10 251
11 255 El limite debe ser
12 259 menor o igual al
valor máximo
13 263 271≤271
14 267
15 271

10. INTERVALOS APARENTES
INTERVAL LIMITE LIMITE
O NUMERO
INFERIOR SUPERIOR
Para determinar el
1 215 218 limite superior se
toma en cuanta el
2 219 219-1 segundo limite
superior osease 219
3 223
A este se le resta -1
4 227
5 231
6 235
7 239
8 243
9 247
10 251
11 255
12 259
13 263
14 267
15 271

11. INTERVAL LIMITE LIMITE
O NUMERO
INFERIOR SUPERIOR
1 215 218
2 219 222
Vamos ir
3 223 226 sumando el
4 227 230 tamaño del
5 231 234 intervalo
218+4 =222
6 235 238 222+4=226
7 239 242
8 243 246
9 247 250
10 251 254
11 255 258
Este valor debe ser
12 259 262 mayor o igual al
13 263 266 valor máximo
14 267 270 274≥271
15 271 274

12. INTERVAL LIMITE LIMITE
O NUMERO
INFERIOR SUPERIOR
1 215 218 Si podemos observar
los cuatro valores
2 219 222 cumplen con las
condiciones
3 223 226
necesarias.
4 227 230
5 231 234
6 235 238
7 239 242
8 243 246
9 247 250
10 251 254
11 255 258
12 259 262
13 263 266
14 267 270
15 271 274

13. NOTAS
• En dado caso que el intervalo no haya cumplido
con las especificaciones , solo es necesario
aumentar el valor inicial una unidad.
• Si al aumentar el valor inicial no es suficiente y
aumentar el tamaño del intervalo tampoco
cumplen todas las especificaciones .
• Es necesario cambiar el numero de intervalos.