Un intervalo de confianza es un rango de valores que se estima probablemente incluya un parámetro desconocido de la población con un cierto nivel de confianza. Cuanto más amplio es el intervalo, mayor es la probabilidad de que incluya el parámetro, pero menos precisa es la estimación. Los intervalos de confianza se calculan a partir de datos de una muestra y se usan comúnmente niveles de confianza del 95% y 99%.

2.  En estadística, se llama intervalo de confianza a un par de
números entre los cuales se estima que estará cierto valor
desconocido con una determinada probabilidad de acierto.
Formalmente, estos números determinan un intervalo, que se
calcula a partir de datos de una muestra, y el valor
desconocido es un parámetro poblacional. La probabilidad de
éxito en la estimación se representa con 1 - α y se denomina
nivel de confianza. En estas circunstancias, α es el llamado
error aleatorio nivel de significación, esto es, una medida de
las posibilidades de fallar en la estimación mediante tal
intervalo.

3.  El nivel de confianza y la amplitud del intervalo varían
conjuntamente, de forma que un intervalo más amplio tendrá más
posibilidades de acierto (mayor nivel de confianza), mientras que
para un intervalo más pequeño, que ofrece una estimación más
precisa, aumentan sus posibilidades de error.
 El nivel de confianza y la amplitud del intervalo varían
conjuntamente, de forma que un intervalo más amplio tendrá más
posibilidades de acierto (mayor nivel de confianza), mientras que
para un intervalo más pequeño, que ofrece una estimación más
precisa, aumentan sus posibilidades de error.

4.  En definitiva, un intervalo de confianza al 1 - α por ciento para la
estimación de un parámetro poblacional θ que sigue una
determinada distribución de probabilidad , es una expresión del tipo
[θ1, θ2] tal que P[θ1 ≤ θ ≤ θ2] = 1 - α, donde P es la función de
distribución de probabilidad de θ.
Las líneas verticales representan 50 construcciones
diferentes de intervalos de confianza para la estimación
del valor μ.

5.  De una población de media y desviación típica se
pueden tomar muestras de elementos. Cada una de
estas muestras tiene a su vez una media ( ). Se puede
demostrar que la media de todas las medias muéstrales
coincide con la media poblacional:[2]
 Pero además, si el tamaño de las muestras es lo
suficientemente grande,[3] la distribución de medias
muéstrales es, prácticamente, una distribución normal (o
gaussiana) con media μ y

6.  una desviación típica dada por la siguiente
expresión:
 Esto se representa como sigue
 Si estandarizamos, se sigue que:

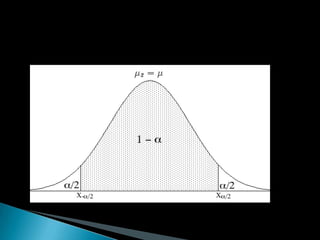
7.  En una distribución Z ~ N(0, 1) puede calcularse fácilmente un intervalo
dentro del cual caigan un determinado porcentaje de las
observaciones, esto es, es sencillo hallar z1 y z2 tales que P[z1 ≤ z ≤
z2] = 1 - α, donde (1 - α)·100 es el porcentaje deseado (véase el uso
de las tablas en una distribución normal).
 Se desea obtener una expresión tal que
 En esta distribución normal de medias se puede calcular el intervalo
de confianza donde se encontrará la media poblacional si sólo se
conoce una media muestral ( ), con una confianza determinada.
Habitualmente se manejan valores de confianza del 95 y del 99 por
ciento. A este valor se le llamará (debido a que es el error que se
cometerá, un término opuesto).

8.  En esta distribución normal de medias se puede calcular el intervalo
de confianza donde se encontrará la media poblacional si sólo se
conoce una media muestral ( ), con una confianza determinada.
Habitualmente se manejan valores de confianza del 95 y del 99 por
ciento. A este valor se le llamará (debido a que es el error que se
cometerá, un término opuesto).
 Para ello se necesita calcular el punto —o, mejor dicho, su versión
estandarizada o valor critico— junto con su "opuesto en la
distribución" . Estos puntos delimitan la probabilidad para el
intervalo, como se muestra en la siguiente imagen: