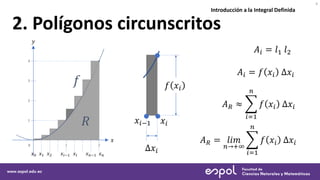
Este documento introduce el concepto de integral definida y cómo se puede usar para calcular el área bajo una curva. Explica cómo aproximar el área usando polígonos inscritos y circunscritos, dividiendo el intervalo en subdivisiones más pequeñas. También presenta los objetivos de determinar el área de una región usando estos métodos y referencias adicionales sobre el tema.