Este documento introduce el concepto de integral definida como el límite de una suma de áreas. Explica cómo dividir un intervalo en subintervalos para aproximar el área bajo una curva mediante rectángulos, y cómo hacer que la suma se aproxime al área total al reducir el tamaño de los subintervalos. También establece las definiciones matemáticas precisas de suma inferior, suma superior e integral de Riemann, y analiza las condiciones para que una función sea integrable.

1. VBV
LA INTEGRAL DEFINIDA
1

2.  Derivada  Recta tangente
 Integral  Área
 Entendemos:
 Área de una función f : región comprendida entre
la función y el eje X, entre dos líneas verticales.
2

3. 3
Pensemos en como obtener el
área bajo la función f
f(x)
Sabemos calcular el área de
polígonos…

4. 4
Podríamos …
x0 x1
x
f(x)
x2 x3 x4
Nosotros construiremos
rectangulos!!!

5. 5
En realidad…
 Este es un problema muy
antiguo (Arquimedes se
plantea esto, pero son
Newton y Leibniz los que
lo resuelven).
 Idea: Construir
rectangulos “bajo” la
curva f(x), encontrar el
área de todos estos
rectangulos.

6. Sea [a,b] un intervalo
cerrado.
 Dividamos el intervalo [a, b] en n sub-intervalos
no necesariamente iguales eligiendo n-1 puntos
entre a y b, y, hagamos x0=a y xn=b de tal forma
que:
x0 < x1 < x2 < x3 < … < xn-2 < xn-1 < xn
 Diremos que P ={x0,x1, . . . ,xn} es una partición de
[a,b]
6

7. Denotemos por Δxi la longitud de
cada sub-intervalo tal que:
Δx1 = x1 – x0
Δx2 = x2 – x1
…
Δxi = xi – xi-1
…
Δxn-1 = xn-1 – xn-2
Δxn = xn – xn-1
Notar que Δxi corresponderá a la
base de cada rectangulo.
7

8.  A la longitud del sub-intervalo (o sub-
intervalos) más largo de la partición P se
llama norma de la partición y se le
denota ||P||.
 Esto es, ||P||= max{Δxi :i=1,…,n}
8

9. Ejemplo:
 Considerar el intervalo [1,3] y construir una
partición donde n=4.
9

10. Pensar en una partición para
[a,b]
 Geométrica:
 a, ar, ar2,… arm, donde r0
 Aritmética:
 a, a+d, a+2d, … a+md
10

11. PARTICIÓN GEOMÉTRICA
 Se define r como la raíz n-ésima del
cuociente: b/a
 Se tiene: xi= x0*rn
 Notar que en esta partición la amplitud de
cada sub-intervalo Δxi NO es constante .
11

12. PARTICIÓN ARITMÉTICA
 Se define d=(b-a)/n
 Se tiene: xi= x0+id
 Notar que en esta partición la amplitud de
cada sub-intervalo Δxi es constante e igual a d.
 Por esto, denotamos Δx=d.
12

13. Pensemos en la altura de
cada rectángulo…
 Sea f : [a,b]  una función acotada
 P ={x0,x1, . . . ,xn} una partición de [a,b]
 Para i = 1, . . . ,n denotamos:
 mi = inf { f (x) : x  [xi-1 , xi ] }
 Mi = sup { f (x) : x  [xi-1 , xi ] }
 Como [a,b] , y f es acotada, entonces cada i el
conjunto { f (x) : x  [xi-1 , xi ] } es no vacío y
acotado, por tanto existen su ínfimo y supremo.
13

14. 14
DEF:
SUMA INFERIOR de f asociada a P
i
n
1
i
iΔx
m
)
,
( 


P
f
s
x1 x2 … xn-1 b=xn
a=x0
f

15. 15
DEF:
SUMA SUPERIOR de f asociada a P
i
n
1
i
iΔx
M
)
,
( 


P
f
S
x1 x2 … xn-1 b=xn
a=x0
f

16. Ejemplo:
 Calcular s(f,P) y S(f,P) en el intervalo [1,3],
para la función f(x)=x2+2
 Usando una partición con n=4.
16

17. Proposición:
 Para cada partición, se verifica:
s(f,P) ≤ S(f,P)
 Dem:
mi ≤ Mi  mi Δxi ≤ Mi Δxi
  mi Δxi ≤  Mi Δxi
 s(f,P) ≤ S(f,P)
17

18. Proposición:
 P1 P2  s(f,P1) ≤ s(f,P2) y S(f,P2) ≤ S(f,P1)
 Dem:
Pensar en agregar puntos (de a uno a la
partición P1).
18

19. Corolario:
 Sean P1 y P2 dos particiones arbitrarias de
[a,b]. Entonces:
 m (b -a) ≤ s(f ,P1) ≤ S(f,P2) ≤ M (b -a)
 Además, si P= P1  P2 , entonces:
 s(f ,P1) ≤ s(f ,P) ≤ S(f,P) ≤ S(f ,P2)
19

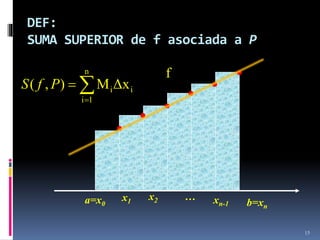
20. DEF:
INTEGRAL INFERIOR de f en
[a,b]
b]}
[a,
de
s
particione
P
:
P)
,
sup{s(f
)
( 

b
a
dx
x
f
20

21. DEF:
INTEGRAL SUPERIOR de f en
[a,b]
 
b
a
dx
x
f b]}
[a,
s
particione
P
:
P)
,
inf{S(f
)
(
21

22. OBS:

b
a
dx
x
f )
(

 
b
a
b
a
dx
x
f
dx
x
f )
(
)
(
22

23. DEF:
 f se dice RIEMANN INTEGRABLE, si:
 Se escribe:

 
b
a
b
a
dx
x
f
dx
x
f )
(
)
(

b
a
dx
x
f )
(
23

24. Pensar en…
 Alguna función que NO sea Riemann
integrable.
24

25. Ejemplo:
 Calcular la integral de Riemann para f(x)=x en
[a,b].
 Considerando las particiones aritméticas:
 Pn= {xi=a+i(b-a)/n, i=1,…,n}
 Se tiene que:
25
n
a
b
a
b
P
f
s n
2
)
(
2
)
,
(
2
2
2




n
a
b
a
b
P
f
S n
2
)
(
2
)
,
(
2
2
2





26. Pensar…
 ¿qué debe suceder para que …
??????
26

 
b
a
b
a
dx
x
f
dx
x
f )
(
)
(

27. Teorema
27
)
,
(
lim
)
,
(
lim
0
||
||
0
||
||
n
P
n
P
P
f
S
P
f
s
n
n 


 Si la norma de la partición Pn se aproxime a
cero, la suma inferior y superior coinciden.
 Esto es
 Notar que es equivalente a decir:
)
,
(
lim
)
,
(
lim
|
|
n
n
n
n
P
f
S
P
f
s






28. OBS:
28
 Si hacemos que la norma de la partición Pn se
aproxime a cero.
 Entonces, la suma de Riemann se aproximará a
un valor A que corresponde a la suma algebraica
de las áreas comprendidas entre la gráfica de la
función y=f(x) y el eje x desde a hasta b.

29. n = 3 rectángulos
Veamos esto geometricamente…

30. n = 6 rectángulos

31. n = 12 rectángulos

32. n = 24 rectángulos

33. n = 48 rectángulos

34. n = 99 rectángulos

35. La integral definida plantea el límite de una
suma de áreas.


b
a
dx
x
f
Área )
(
Interpretación …

36. Teorema
 Considere una sucesión de particiones Pn de
un intervalo [a,b] tales que:
 y,
 Entonces, f es Riemann integrable,
0
||
||
lim 


Pn
n
0
)}
,
(
)
,
(
{
lim 



Pn
f
s
Pn
f
S
n







b
a
n
n
dx
x
f
Pn
f
s
Pn
f
S )
(
)
,
(
lim
)
,
(
lim
36

37. Ejercicios:
1. Construir 10 sub-intervalos para [0,1]
usando la partición:
2. Sea f(x) = x2. Considerar una partición del
intervalo [0,1] en 8 sub-intervalos del mismo
largo. Encontrar las sumas de riemann.
37

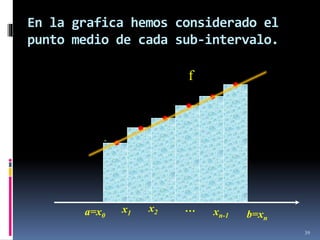
38. Definición:
 Sea f : [a,b]  una función acotada
 P una partición de [a,b]
 Una SUMA DE RIEMANN para la función f
respecto a la partición P es una suma finita de
la forma:
38
]
,
[
;
Δx
)
(
)
,
,
( 1
i
n
1
i
i i
i
i
i x
x
f
P
f
S 


  



39. 39
En la grafica hemos considerado el
punto medio de cada sub-intervalo.
x1 x2 … xn-1 b=xn
a=x0
f

40. 0
y
x
y = f(x)
x0=a xn=b
x1 x2 xn-1
xi
xi-1
• • • • • • • • • •
Δ1x Δ2x Δix Δnx
Δn-1x
… …
•
•
•
•
•
•
•
•
•
•
w1 w2 wi wn-1 wn
Otra grafica…

41. Ejemplo:
 Calcular la suma de riemann en el intervalo
[1,3], para la función f(x)=x2+2
 Usando una partición con n=4.
41

42. OBS:
 Cuando la función considerada es continua la
suma superior e inferior corresponde a la
suma de Riemann.
 Escribimos:
 Para denotar que:
42
L
P
f
S i
n



)
,
,
(
lim 




 






 |
)
,
,
(
|
||
||
.
.
,
0
,
0 L
P
f
S
P
q
t i

43. Propiedades:
 Sean f,g : [a,b]  acotadas e integrables.
 Se cumple:
43
 
 


b
a
b
a
b
a
dx
x
g
dx
x
f
dx
x
g
x
f )
(
)
(
))
(
)
(
(

 
b
a
b
a
dx
x
f
dx
x
f )
(
)
( 


44.  Salvo quizás en un un conjunto finito de puntos.
44
R
dx
x
f
dx
x
f
b
a
b
a

 
 

 ,
)
(
)
(
0
)
(
0
)
( 

 
b
a
dx
x
f
x
f
 





b
a
b
a
dx
x
g
dx
x
f
b
a
x
x
g
x
f )
(
)
(
]
,
[
),
(
)
(
 

b
a
b
a
dx
x
f
dx
x
f |
)
(
|
)
(

45. Proposición(Aditividad):
 Si f : [a,b]  es acotada e integrable, y para
todo c  [a , b] .
 Se cumple:
 f es integrable en los intervalos [a , c ] y [c , b].
 Además se verifica el reciproco.
45
 
 

c
a
b
c
b
a
dx
x
f
dx
x
f
dx
x
f )
(
)
(
)
(

46. Ejercicio
Sea f una función continua en 1, 5, si:

 


5
1
3
1
7
)
(
4
)
( dx
x
f
y
dx
x
f
Determine el valor de:

5
3
)
( dx
x
f

47. Definición:
 Sea f : [a,b]  acotada e integrable.
 Definimos:
47
0
)
(
 
a
a
dx
x
f

 

a
b
b
a
dx
x
f
dx
x
f )
(
)
(

48. Teorema:
 S f : [a,b]  es monótona entonces f es
integrable.
48

49. Observación
 Muchas de las funciones con las cuales se
trabaja en cálculo son monótonas por
intervalos.
 Por la propiedad de aditividad y este teorema
podemos argumentar la integrabilidad de
prácticamente todas las funciones
 elementales como por ejemplo ex ,
lnx,arctanx,etc.
49

50. Teorema:
 S f : [a,b]  es continua entonces f es
integrable.
50

51. Teorema:
 Si f : [a,b]  es continua en [a , b] excepto
en x0 , x1 , x2 , …, xn
 Entonces, f es integrable en [a,b].
 Además, se verifica:
51
  
 



o
o n
x
a
x
x
b
x
b
a
dx
x
f
dx
x
f
dx
x
f
dx
x
f
1
)
(
...
)
(
)
(
)
(

52. Definición:
 Sea f : [a,b]  integrable .
 se define elVALOR PROMEDIO de f en [a,b]
por:
52



b
a
dx
x
f
a
b
f
AV )
(
1
)
(

53. Teorema:
 Sea f : [a,b]  continua.
 Entonces existe c[a,b] tal que f ( c ) = AV(f).
53

54. Ejercicios
 Calcular:
 Dem.
 ¿Qué valores de a y b maximizan el valor de
54
 
4
0
]
[
)
2
( dx
x
a
b
b
a
x
e
e
dx
e 


 
b
a
dx
x
x )
( 2

55. ?
3
40
)
4
1
(
3
2
2





dx
x
 Justificando su respuesta, responda lo siguiente:
¿Será correcto afirmar que:
a)
b)
1
0
1
0
2
1
1
2
)
1
(
2
)
1
(
1
2
)
1
(
1





 


x
dx
x
dx
x

56. Determine el valor de “ ” tal que:
2
)
2
3
(
1
2



dx
x
x
k
k

57.  Se muestra al grafica de f . Usando fórmulas geométricas.
 Evaluar y calcular el área representada por la
 integral.

f

9
3
)
( dx
x
f

9
3
)
( dx
x
f

58. 








2
1
;
2
1
1
1
-
;
2
-
x
)
(
x
x
x
x
f
 


2
1
dx
x
f
 Sea:
 Calcular