Este documento trata sobre los conceptos básicos de la integral definida y sus propiedades. Explica que la integral definida representa el área bajo una curva entre dos límites y puede calcularse como el límite de la suma de Riemann. También describe propiedades como la linealidad y reglas como la regla de Barrow para calcular la integral definida en términos de la primitiva.

1. INTEGRAL DE UN INTERVALO
INTEGRAL DEFINIDA
SEMANA 15

2. INTEGRAL
INTEGRAL
INDEFINIDA NTEGRAL DEFINIDA
Primitiva Definición Cálculo
Área bajo la
curva Suma de Reimann Teoremas
Propiedades
Primitivas
inmediatas Definida Fundamental del Cálculo Valor medio
Área
Integral Propiedades
Por partes Regla de Barrow
Cambio de
variable
Descomposiciónen
fracciones simples
Cambio de
variable

9. • La suma de Riemann
representa la suma de los n rectángulos. Si la norma de la
partición tiende a cero implica que el número de celdas se
incrementa, es decir que cada vez se tienen más y más
rectángulos que se aproximan al área real bajo la curva. Por lo
tanto, por definición: la integral definida es el área bajo la
curva en sus límites.

10. Área bajo una curva
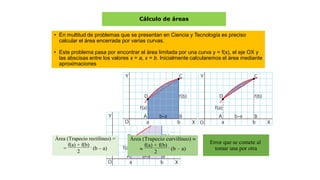
• Suponiendo f(x) acotada y positiva, la región limitada por la
gráfica de f y el eje OX en el intervalo [a, b] se denota por R(f;
[a, b]).

11. Cálculo de áreas
• En multitud de problemas que se presentan en Ciencia y Tecnología es preciso
calcular el área encerrada por varias curvas.
• Este problema pasa por encontrar el área limitada por una curva y = f(x), el eje OX y
las abscisas entre los valores x = a, x = b. Inicialmente calcularemos el área mediante
aproximaciones
Área (Trapecio rectilíneo) =
=
f(a) + f(b)

.
(b – a)
Área (Trapecio curvilíneo) 

f(a) + f(b)

.
(b – a)
Error que se comete al
tomar una por otra

12. Integral definida
Cuando se aplica el proceso anterior a cualquier función (no necesariamente positiva)
en el intervalo [a, b] obtenemos las sumas superiores e inferiores de Riemann sobre la
partición Pn.
s(f; Pn) = m1 .  x1 + m2 .  x2 + ... + mn .  xn
S(f; Pn) = M1 .  x1 + M2 .  x2 + ... + Mn .  xn
Sea mi el mínimo de f(x) en Ii = [xi-1, xi]
Sea Mi el máximo de f(x) en Ii = [xi-1, xi]
Si la función f es continua al considerar las particiones con mayor número de
intervalos de manera que la longitud de estos tienda a decrecer, las sumas de
Riemann se acercan a un número que se llama integral definida de la función f en
[a, b] y se escribe 


a
b f(x) dx .

13. Propiedades de la integral definida
2. ( ) 0.
a
a
f x dx =
3. ( ) siendo un número real.
b
a
kdx k b a k= −
( )4. ( ) ( ) ( ) ( ) .
b b b
a a a
f x g x dx f x dx g x dx =   
5. ( ) ( ) siendo un número real.
b b
a a
kf x dx k f x dx k= 
1. ( ) ( ) .
a b
b a
f x dx f x dx= − 

14. Propiedades de la integral definida
8. Si ( ) ( ) para todo [ , ],
( ) ( ) .
b b
a a
f x g x x a b
f x dx g x dx
 
 
9. Si ( ) para todo [ , ],
( ) ( ) ( ).
b
a
n f x m x a b
n b a f x dx m b a
  
−   −
.)()(.10  
b
a
b
a
dxxfdxxf
7. Si ( ) 0 para todo [ , ], ( ) 0.
b
a
f x x a b f x dx  
6. ( ) ( ) ( ) para cualquier [ , ].
b c b
a a c
f x dx f x dx f x dx c a b= +   

15. Función área o función integral
Dada una función f(x) continua y positiva en [a, b], se define la función integral
F(x) como la función que mide el área sombreada bajo f. Se representa por:
 =
x
a
xFdttf )()(

16. Función área o función integral
Dada una función f(x) continua y positiva en [a, b], se define la función integral
F(x) como la función que mide el área sombreada bajo f. Se representa por:
 =
x
a
xFdttf )()(

17. Regla de Barrow
‫׬‬𝑎
𝑏
𝑓 𝑥 𝑑𝑥 = I(x) I I(b)- I(a)

18. • ‫׬‬1
2
3𝑥2 + 2𝑑𝑥 = 3
𝑥3
3
+ 2𝑥 ‫׬‬1
2
= [ x3+2x] ‫׬‬1
2
= (23+2.2)−(13+2.1) = 12 − 3 = 9
Primer ejemplo
Segundo ejemplo

19. ‫׬‬1
2
𝑥2 𝑑𝑥 =
𝑥3
3
‫׬‬1
2
=
23
3
−
13
3
=
8
3
−
1
3
=
8−1
3
=
7
3
Tercer ejemplo

20. • Cuarto ejemplo

21. EJERCICIOS

22. Ejercicios