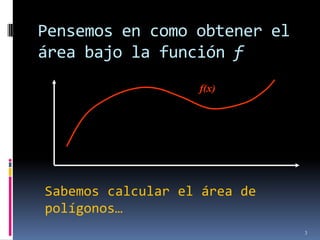
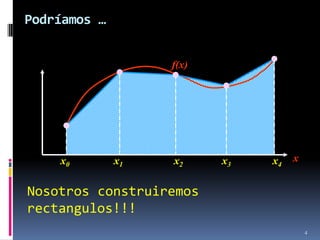
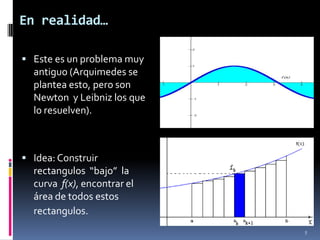
Este documento presenta los conceptos básicos de la integral definida. Explica que la integral representa el área bajo una curva y que se puede calcular dividiendo el intervalo en subintervalos para construir rectángulos de base Δx y altura f(x). También introduce las sumas inferior y superior como límites del área y la definición formal de integral definida como el límite de dichas sumas cuando la partición tiende a cero.

1. NAUDY HERNANDEZ
UNIVERSIDAD FERMIN TORO
LA INTEGRAL DEFINIDA
VBV
1

2.  Derivada  Recta tangente
 Integral  Área
 Entendemos:
 Área de una función f : región comprendida entre
la función y el eje X, entre dos líneas verticales.
2

3. Pensemos en como obtener el
área bajo la función f
f(x)
Sabemos calcular el área de
polígonos…
3

4. Podríamos …
f(x)
x0 x1 x2 x3 x4 x
Nosotros construiremos
rectangulos!!!
4

5. En realidad…
 Este es un problema muy
antiguo (Arquimedes se
plantea esto, pero son
Newton y Leibniz los que
lo resuelven).
 Idea: Construir
rectangulos “bajo” la
curva f(x), encontrar el
área de todos estos
rectangulos.
5

6. Sea [a,b] un intervalo
cerrado.
 Dividamos el intervalo [a, b] en n sub-intervalos
no necesariamente iguales eligiendo n-1 puntos
entre a y b, y, hagamos x0=a y xn=b de tal forma
que:
x0 < x1 < x2 < x3 < … < xn-2 < xn-1 < xn
 Diremos que P ={x0,x1, . . . ,xn} es una partición de
[a,b]
6

7. Denotemos por Δxi la longitud de
cada sub-intervalo tal que:
Δx1 = x1 – x0
Δx2 = x2 – x1
…
Δxi = xi – xi-1
…
Δxn-1 = xn-1 – xn-2
Δxn = xn – xn-1
Notar que Δxi corresponderá a la
base de cada rectangulo.
7

8.  A la longitud del sub-intervalo (o sub-
intervalos) más largo de la partición P se
llama norma de la partición y se le denota
||P||.
 Esto es, ||P||= max{Δxi :i=1,…,n}
8

9. Ejemplo:
 Considerar el intervalo [1,3] y construir una
partición donde n=4.
9

10. Pensar en una partición para
[a,b]
 Geométrica:
 a, ar, ar2,… arm, donde r 0
 Aritmética:
 a, a+d, a+2d, … a+md
10

11. PARTICIÓN GEOMÉTRICA
 Se define r como la raíz n-ésima del
cuociente: b/a
 Se tiene: xi= x0*rn
 Notar que en esta partición la amplitud de
cada sub-intervalo Δxi NO es constante .
11

12. PARTICIÓN ARITMÉTICA
 Se define d=(b-a)/n
 Se tiene: xi= x0+id
 Notar que en esta partición la amplitud de
cada sub-intervalo Δxi es constante e igual a d.
 Por esto, denotamos Δx=d.
12

13. Pensemos en la altura de
cada rectángulo…
 Sea f : [a,b]  una función acotada
 P ={x0,x1, . . . ,xn} una partición de [a,b]
 Para i = 1, . . . ,n denotamos:
 mi = inf { f (x) : x [xi-1 , xi ] }
 Mi = sup { f (x) : x [xi-1 , xi ] }
 Como [a,b] , y f es acotada, entonces cada i el
conjunto { f (x) : x [xi-1 , xi ] } es no vacío y
acotado, por tanto existen su ínfimo y supremo.
13

14. DEF:
SUMA INFERIOR de f asociada a P
n f
s( f , P) m i Δx i
i 1
a=x0 x1 x2 … xn-1 b=xn
14

15. DEF:
SUMA SUPERIOR de f asociada a P
n f
S ( f , P) M i Δx i
i 1
a=x0 x1 x2 … xn-1 b=xn
15

16. Ejemplo:
 Calcular s(f,P) y S(f,P) en el intervalo [1,3],
para la función f(x)=x2+2
 Usando una partición con n=4.
16

17. Proposición:
 Para cada partición, se verifica:
s(f,P) ≤ S(f,P)
 Dem:
m i ≤ Mi mi Δxi ≤ Mi Δxi
mi Δxi ≤ Mi Δxi
s(f,P) ≤ S(f,P)
17

18. Proposición:
 P1 P2 s(f,P1) ≤ s(f,P2) y S(f,P2) ≤ S(f,P1)
 Dem:
Pensar en agregar puntos (de a uno a la
partición P1).
18

19. Corolario:
 Sean P1 y P2 dos particiones arbitrarias de
[a,b]. Entonces:
 m (b -a) ≤ s(f ,P1) ≤ S(f,P2) ≤ M (b -a)
 Además, si P= P1 P2 , entonces:
 s(f ,P1) ≤ s(f ,P) ≤ S(f,P) ≤ S(f ,P2)
19

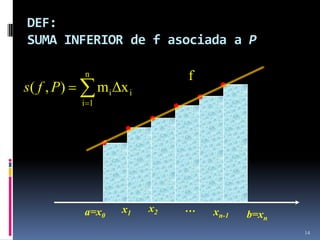
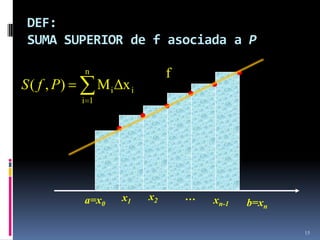
20. DEF:
INTEGRAL INFERIOR de f en
[a,b]
b
f ( x)dx sup{s(f , P) : P particione s de [a, b]}
a
20

21. DEF:
INTEGRAL SUPERIOR de f en
[a,b]
b
f ( x)dx inf{S(f , P) : P particione s [a, b]}
a
21

22. OBS:
b b
b
f ( x)dx
a
f ( x)dx
f ( x)dx
a a
22

23. DEF:
 f se dice RIEMANN INTEGRABLE, si:
b b
f ( x)dx f ( x)dx
a a
 Se escribe: b
f ( x)dx
a
23

24. Pensar en…
 Alguna función que NO sea Riemann
integrable.
24

25. Ejemplo:
 Calcular la integral de Riemann para f(x)=x en
[a,b].
 Considerando las particiones aritméticas:
 Pn= {xi=a+i(b-a)/n, i=1,…,n}
 Se tiene que:
2 2 2
b a (b a)
s( f , Pn )
2 2n
2 2 2
b a (b a)
S ( f , Pn )
2 2n 25

26. Pensar…
 ¿qué debe suceder para que …
b b
f ( x)dx f ( x)dx
a a
??????
26

27. Teorema
 Si la norma de la partición Pn se aproxime a
cero, la suma inferior y superior coinciden.
 Esto es
lim s( f , Pn ) lim S ( f , Pn )
||Pn || 0 ||Pn || 0
 Notar que es equivalente a decir:
lim s( f , Pn ) lim S ( f , Pn )
|n |n
27

28. OBS:
 Si hacemos que la norma de la partición Pn se
aproxime a cero.
 Entonces, la suma de Riemann se aproximará a
un valor A que corresponde a la suma algebraica
de las áreas comprendidas entre la gráfica de la
función y=f(x) y el eje x desde a hasta b.
28

29. Veamos esto geometricamente…
n = 3 rectángulos

30. n = 6 rectángulos

31. n = 12 rectángulos

32. n = 24 rectángulos

33. n = 48 rectángulos

34. n = 99 rectángulos

35. Interpretación …
La integral definida plantea el límite de una
suma de áreas.
b
Área f ( x) dx
a

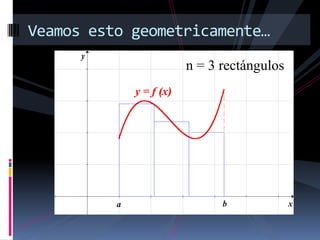
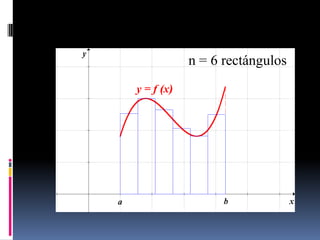
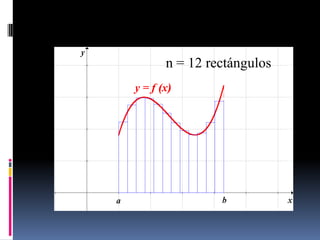
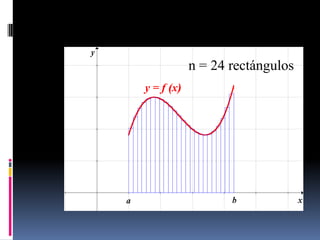
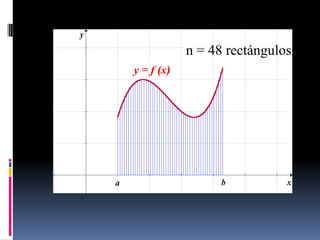
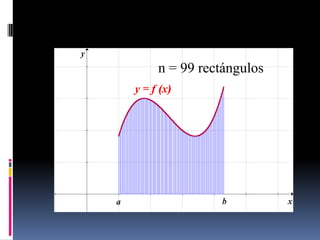
36. Teorema
 Considere una sucesión de particiones Pn de
un intervalo [a,b] tales que:
lim || Pn || 0
n
 y,
lim {S ( f , Pn) s( f , Pn)} 0
n
 Entonces, f es Riemann integrable,
b
lim S ( f , Pn) lim s( f , Pn) f ( x)dx
n n
a
36

37. Ejercicios:
1. Construir 10 sub-intervalos para [0,1]
usando la partición:
2. Sea f(x) = x2. Considerar una partición del
intervalo [0,1] en 8 sub-intervalos del mismo
largo. Encontrar las sumas de riemann.
37

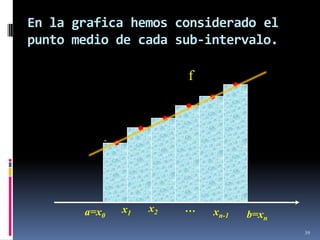
38. Definición:
 Sea f : [a,b]  una función acotada
 P una partición de [a,b]
 Una SUMA DE RIEMANN para la función f
respecto a la partición P es una suma finita de
la forma:
n
S ( f , P, i ) f ( i )Δx i ; i [ xi 1 , xi ]
i 1
38

39. En la grafica hemos considerado el
punto medio de cada sub-intervalo.
f
a=x0 x1 x2 … xn-1 b=xn
39

40. Otra grafica…
y
•
•
• y = f(x)
•
• •
•
w1 w2 wi wn-1 wn
x0=a• x1 • x2 •0 •x• x • • • • x • x =b x
i-1 i • n-1 n
•
Δ1x Δ2x … Δix … • Δn-1x Δnx

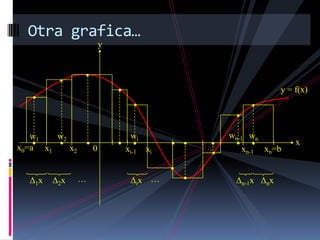
41. Ejemplo:
 Calcular la suma de riemann en el intervalo
[1,3], para la función f(x)=x2+2
 Usando una partición con n=4.
41

42. OBS:
 Cuando la función considerada es continua la
suma superior e inferior corresponde a la
suma de Riemann.
 Escribimos:
lim S ( f , P, i ) L
n
 Para denotar que:
0, 0, t.q. || P || | S ( f , P, i ) L |
42

43. Propiedades:
 Sean f,g : [a,b]  acotadas e integrables.
 Se cumple:
b b b
( f ( x) g ( x)) dx f ( x)dx g ( x)dx
a a a
b b
f ( x)dx f ( x)dx
a a
43

44. b b
f ( x)dx f ( x)dx, R
a a
b
f ( x) 0 f ( x)dx 0
a
b b
f ( x) g ( x), x [a, b] f ( x)dx g ( x)dx
a a
 Salvo quizás en un un conjunto finito de puntos.
b b
f ( x)dx | f ( x) | dx
a a 44

45. Proposición(Aditividad):
 Si f : [a,b]  es acotada e integrable, y para
todo c [a , b] .
 Se cumple:
 f es integrable en los intervalos [a , c ] y [c , b].
 Además se verifica el reciproco.
b c b
f ( x)dx f ( x)dx f ( x)dx
a a c
45

46. Ejercicio
Sea f una función continua en 1, 5 , si:
3 5
f ( x) dx 4 y f ( x) dx 7
1 1
Determine el valor de:
5
f ( x ) dx
3

47. Definición:
 Sea f : [a,b]  acotada e integrable.
 Definimos:
a
f ( x)dx 0
a
b a
f ( x)dx f ( x)dx
a b
47

48. Teorema:
 S f : [a,b]  es monótona entonces f es
integrable.
48

49. Observación
 Muchas de las funciones con las cuales se
trabaja en cálculo son monótonas por
intervalos.
 Por la propiedad de aditividad y este teorema
podemos argumentar la integrabilidad de
prácticamente todas las funciones
 elementales como por ejemplo ex ,
lnx,arctanx,etc.
49

50. Teorema:
 S f : [a,b]  es continua entonces f es
integrable.
50

51. Teorema:
 Si f : [a,b]  es continua en [a , b] excepto
en x0 , x1 , x2 , …, xn
 Entonces, f es integrable en [a,b].
 Además, se verifica:
b xo x1 b
f ( x)dx f ( x)dx f ( x)dx ... f ( x)dx
a a xo xn
51