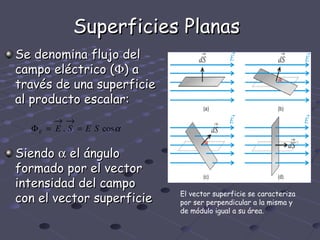
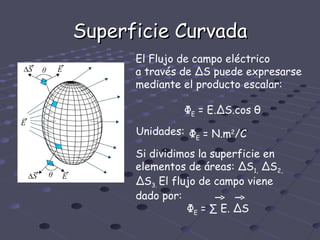
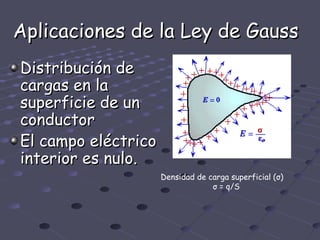
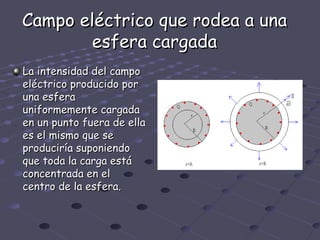
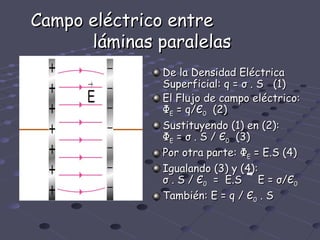
La Ley de Gauss establece que el flujo del campo eléctrico a través de una superficie cerrada es igual a la carga encerrada en su interior dividida por la permitividad del medio. Se utiliza para determinar el campo eléctrico en superficies con alto grado de simetría cuando la magnitud de E es constante y su dirección es perpendicular a la superficie. Algunas aplicaciones incluyen la distribución de cargas en la superficie de un conductor y el campo eléctrico que rodea una esfera cargada uniformemente.