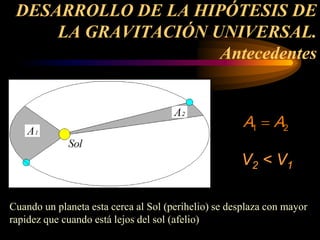
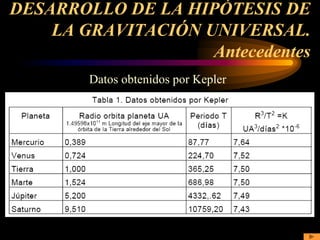
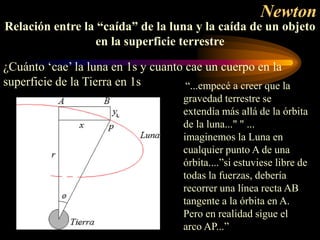
Este documento describe el desarrollo de la hipótesis de la gravitación universal de Newton. Explica los antecedentes como las leyes de Kepler y el trabajo de Galileo y Newton. Luego, detalla cómo Newton dedujo que la fuerza que mantiene a los planetas en órbita decrece con el cuadrado de la distancia, al igual que la fuerza de la gravedad terrestre. Finalmente, muestra cómo Newton comprobó con éxito su teoría al calcular el período orbital de la Luna.

1. PRINCIPIO DE LA
GRAVITACIÓN UNIVERSAL.
• FUERZA GRAVITACIONAL Newton (1685)
2
r
GMm
F =
r
r
GMm
F ˆ
2
−
=

2
r
GMm
F =
2
GMm
F
r
=
2
ˆ
GMm
F r
r
= −


2. 2 1
21
21
Gm m
F
r
= −

3. DESARROLLO DE LA HIPÓTESIS DE
LA GRAVITACIÓN UNIVERSAL.
Antecedentes
• leyes que regían los cuerpos en caída libre sobre la
superficie de la Tierra - Galileo,
• leyes del movimiento con aceleración constante,
• todos los objetos caen sobre la superficie de la
Tierra con la misma aceleración g
• se había calculado g = 9.8 m/s2

4. DESARROLLO DE LA HIPÓTESIS DE
LA GRAVITACIÓN UNIVERSAL.
Antecedentes
• Newton había formulado las tres “leyes de Newton”
Segunda Ley Newton
F ma
=
 
F ma
=

5. DESARROLLO DE LA HIPÓTESIS
DE LA GRAVITACIÓN UNIVERSAL.
Antecedentes
• Se había definido la aceleración centrípeta
2
r
v
a
r
= −
r r
F ma
= −

6. DESARROLLO DE LA HIPÓTESIS DE
LA GRAVITACIÓN UNIVERSAL.
Antecedentes
• hipótesis de Copérnico (1473-1543).
tierra esférica,
sol quieto y los planetas girando alrededor del sol en planos
coincidentes con períodos de revolución proporcional al
tamaño de las órbitas
• observaciones astronómicas de Tycho Brahe (1546 -
1601).
• Se aceptaban las tres leyes de Kepler

7. DESARROLLO DE LA HIPÓTESIS DE
LA GRAVITACIÓN UNIVERSAL.
Antecedentes
Primera ley de Kepler : Los planetas se mueven en órbitas
elípticas, con el Sol en uno de los focos

8. DESARROLLO DE LA HIPÓTESIS DE
LA GRAVITACIÓN UNIVERSAL.
Antecedentes
Cuando un planeta esta cerca al Sol (perihelio) se desplaza con mayor
rapidez que cuando está lejos del sol (afelio)
1 2
A A
=
V2 < V1

9. DESARROLLO DE LA HIPÓTESIS DE
LA GRAVITACIÓN UNIVERSAL
Tercera ley de Kepler : Si el período de rotación de dos
planetas es T1 y T2 y las distancias medias al sol son R1 y R2,
La relación entre T1 , T2 , R1 R2
3 2
1 1
2 2
R T
R T
   
=
   
   
3 3
1 2
2 2
1 2
R R
k
T T
= =
•K es una constante para todos los cuerpos que giran alrededor
de una masa central

10. DESARROLLO DE LA HIPÓTESIS DE
LA GRAVITACIÓN UNIVERSAL.
Antecedentes
Datos obtenidos por Kepler

11. DESARROLLO DE LA HIPÓTESIS DE
LA GRAVITACIÓN UNIVERSAL.
Newton
Newton acepta el modelo planetario de Copérnico
Planetas cuerpos esféricos giran en órbitas circulares
con el Sol como centro.
Supone la gravitación una ley universal.
las leyes que rigen la caída de los cuerpos en la
superficie de la Tierra son las mismas que rigen las
fuerzas que mantienen en órbitas a los planetas
alrededor del Sol

12. DESARROLLO DE LA HIPÓTESIS DE
LA GRAVITACIÓN UNIVERSAL.
Newton
Análisis de las observaciones de Kepler
Segunda Ley de Kepler
Movimiento bajo fuerzas centrales, el radio vector de la
partícula barre áreas iguales en tiempos iguales.
Fuerza de atracción en sentido contrario del vector posición
La fuerza que mueve los planetas no es en dirección de la
trayectoria, es una fuerza central que actúa perpendicular
a la trayectoria

13. DESARROLLO DE LA HIPÓTESIS DE
LA GRAVITACIÓN UNIVERSAL.
Newton
Análisis de las observaciones de Kepler
Tercera Ley de Kepler
Demostró: si se cumple la 3 ley de Kepler,
la magnitud de la fuerza entre el planeta y el Sol deberá ser
una fuerza proporcional al inverso de la distancia al
cuadrado de los dos cuerpos
2
1
F
r
∝
donde r es el radio medio de la órbita del planeta.

14. Newton
Análisis de las observaciones de Kepler
objeto en órbita de radio r , la aceleración centrípeta es
aceleración de un cuerpo de masa m es:
2
2
2
4
r r
r
r
F m a
m r
F
T
c
F m
π
=
= −
= −
2
2
r
v
a
r
r
v
T
π
= −
=
2 3
T k r
=
2 2 2
r 2 2
4
π
r 4
a = - = -
T r T

15. Newton
“...empecé a creer que la
gravedad terrestre se
extendía más allá de la órbita
de la luna..." " ...
imaginemos la Luna en
cualquier punto A de una
órbita....”si estuviese libre de
todas la fuerzas, debería
recorrer una línea recta AB
tangente a la órbita en A.
Pero en realidad sigue el
arco AP...”
Relación entre la “caída” de la luna y la caída de un objeto
en la superficie terrestre
¿Cuánto ‘cae’ la luna en 1s y cuanto cae un cuerpo en la
superficie de la Tierra en 1s

16. Newton
Relación entre la “caída” de la luna y la caída de un objeto
en la superficie terrestre
O centro de la Tierra la Luna ha “caído” YL en un segundo
calcula cuánto cae la luna en 1 s y la compara con la distancia que
recorre un objeto que cae en este mismo tiempo en la Tierra
2
0
2
L
y
r
≈
2
2
L
x
y
r
=
2
2
L
s r
x s
s
y
r
θ
=
≅
=

17. θ
sen
r
x =
θ
r
x =
En un segundo la luna recorre horizontalmente
2
1
L
r
s s
T
π
= ⋅
Si se toma r = 3.8 x 108 m y TL = 27,3 días
8
6
2 3.8 10 1
1000 1
2.36 10
m s
s m km
s
π × ⋅
≈
=
×
En un segundo la luna “cae”
2 2
3
8
( 1000 )
1.3 10
2 2 3.8 10
L
s m
y m
r m
−
= = = ×
× ×

18. θ
sen
r
x =
θ
r
x =
2
1
2 4.9
T
y g t m
= ≅
3
4
1.3 10 1
2.65 10
4.9 3600
L
T
m
y
y m
−
−
×
≈ × ≈
¿Qué distancia yT recorre en 1 s cuerpo que cae hacia Tierra?
relaciona estas dos distancias,
8
6
3.8 10
60
6.73 10
m
r
R m
×
≈
×
2
1 1
3600
L
T
y
y r
R
= =
 
 
 
relaciona las distancias de
"caída" de la luna y la
distancia que cae un cuerpo
en la Tierra y los radios de la
órbita de la luna y del cuerpo
que cae

19. θ
sen
r
x =
θ
r
x =
1 s la variación del ángulo θ es muy pequeño y si
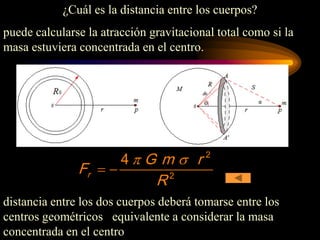
¿Cuál es la distancia entre los cuerpos?
puede calcularse la atracción gravitacional total como la suma
de las atracciones de varias capas esféricas.
2
cos
x
G dM m
dF
s
ϕ
= −
[ ]
2
2 2 2
4
2 2 4
x
k r k r G m r
F r r r
R R R
π σ
=
− + =
− ⋅ =
−
2 2
2 2 2
R r R r
x
R r R r
k r k r
R r
F ds ds
R s R
+ +
− −
 
 
−
=
− +
 
 
 
 
∫ ∫
2
2
dM r sen d
σ π θ θ
=

20. θ
sen
r
x =
θ
r
x =
1 s la variación del ángulo θ es muy pequeño y si
¿Cuál es la distancia entre los cuerpos?
puede calcularse la atracción gravitacional total como si la
masa estuviera concentrada en el centro.
2
2
4
r
G m r
F
R
π σ
= −
distancia entre los dos cuerpos deberá tomarse entre los
centros geométricos equivalente a considerar la masa
concentrada en el centro

21. Newton
M
m
F ∝
2
r
M
m
F ∝
2
r
M
m
G
F =
Una vez sustentadas las hipótesis:
•ley del inverso a la distancia al cuadrado
•fuerzas centrales
•distancias tomadas desde el centro de masas de los cuerpos
•fuerza gravitacional entre dos cuerpos de masas m y M
concluye su hipótesis sobre la gravitación universal.
F m M
∝
2
m M
F
r
∝ 2
G m M
F
r
=

22. Newton
2
L L
C
TL
M V
F =
R
M
m
F ∝
2
r
M
m
F ∝
2
r
M
m
G
F =
Prueba de la hipótesis propuesta
calcular T de la Luna alrededor de la Tierra a partir
de LGU y comparar este con el T medido
2
T
G m M
m g
R
=
2
T
GM gR
=
2
2
L
TL T
LT
m
F g R
R
= ⋅
2
2 2 2
2
2
2 4
TL TL
L
L L
R R
v
T T
π π
 
= =
 
 

23. Newton
M
m
F ∝
2
r
M
m
F ∝
2
r
M
m
G
F =
Prueba de la hipótesis propuesta
2
3 24 3
6
2 3.8 10
6.4 10 9.8
L m
s
m
T
m
π ×
=
×
TL = 2.3231 x 106s ⇒ 26.88 días ≅ 27 días
TL C
( F ) = ( F )
2 2 2
2 2
4
L LT L T
L LT LT
m R m g R
T R R
π
=
3
2 LT
L
T
R
T
R g
π
=

24. La constante de Cavendish (1797)
Cavendish utilizó una balanza de torsión
G = 6.67 10-11 new.m2kg-2 o G = 6.67 10-11 m3s-2kg-1
(sistema mks)
G = 6.67.10-8 dinas cm2 g-2 o G = 6.67.10-8 cm3s-2g-1
(sistema cgs)
1 2
2
G m m
F
d
=
2
1 2
F r
G
m m
=

25. Unidades
Las unidades de la Fuerza Gravitacional son:
Newton (sistema mks)
Dina (sistema cgs)
1 Newton = 105 dina

26. Cálculo de masa y densidad de la Tierra
LGU inicia modelamiento de la estructura de la Tierra
permitió calcular Masa y Densidad suponiendo que esta fuera
esférica.
ρt ≅ 5.52 g/cm3.
Dos siglos después se estableció la variación de la densidad de
la Tierra a través de la sismología, geofísica, planetología,
geología , entre otros
2
G m M
F m g
R
=
2
R g
M
G
=
M
V
ρ =
2
3
4
3
3
4
R g
g
G
R G R
ρ
π π
= = = 5.45 g/cm3
3
4
3
V R
π
=