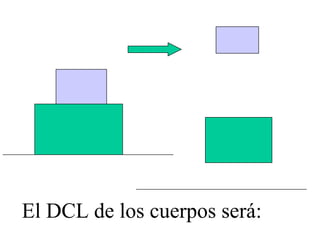
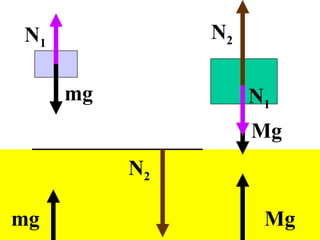
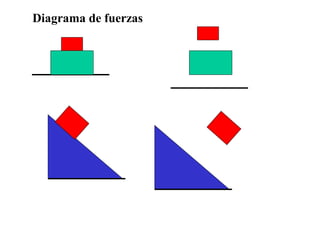
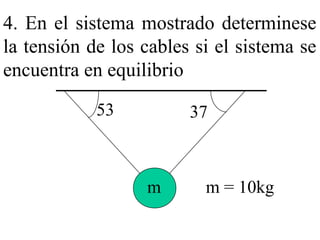
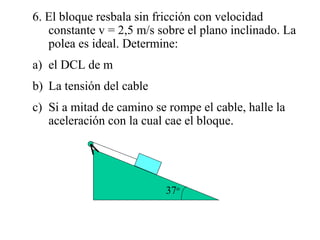
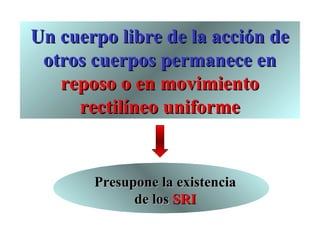
Este documento presenta un resumen de las leyes fundamentales de la mecánica clásica. Explica la primera ley de Newton sobre la inercia y el movimiento rectilíneo uniforme. Luego introduce la segunda ley sobre la relación entre fuerza, masa y aceleración. Finalmente, resume la tercera ley sobre la acción y reacción iguales y de sentido contrario entre dos cuerpos en interacción. El documento provee los conceptos básicos necesarios para comprender la dinámica newtoniana.

1. Leyes de la
mecánica
clásica

2. C 3 DINÁMICA (1)
• Primera ley de Newton.
• Fuerza. Masa. Segunda ley de Newton.
Unidades de fuerza.
•Cantidad de movimiento lineal.
Generalización de la segunda ley de Newton.
•Tercera ley de Newton.
• Sistemas de partículas.
•Bibliog. Sears, Física Universitaria

3. Mecánica de
Investiga las causas
que provocan el
los cuerpos
movimiento mecánico.
macroscópicos
Movimiento
Cinemática
Dinámica
Dinámica
mecánico

4. Problema Central de la
Mecánica Clásica
1- Se tiene un sistema físico a estudiar, del
cual conocemos sus propiedades (masa,
volumen, carga eléctrica, etc.)
2- El sistema se halla inicialmente en una
posición conocida (ya se ha definido el SRI
con observador), con una velocidad conocida,
en un entorno con el cual entra en
interacción.
3- ¿Cómo será el movimiento del sistema en
instantes posteriores?
Cinemática
Dinámica

5. S
Leyes de Fuerzas:
etc. a partir de las
propiedades del sistema
V0 Masa
y de su entorno
y0 M
t0
Volumen x0 Carga
z0 V Q
entorno ?

6. El problema de la Mecánica
Clásica
Fue resuelto por Isaac Newton
(1642-1727) bajo la óptica de la
relatividad de Galileo, cuando
promulgó sus leyes del
movimiento y formuló la ley de
la gravitación universal

7. Primera ley de Newton
Inercia es la ley de la inercia. Inercia eslos
Suele llamarse oposición que presentan la
cuerpos al cuerpos de su estado de
tendencia de los cambio a permanecer en reposo o
en movimiento rectilíneo y uniforme.
movimiento.
Un cuerpo libre de la acción de
otros cuerpos permanece en
reposo o en movimiento
rectilíneo uniforme

8. Un cuerpo libre de la acción de
otros cuerpos permanece en
reposo o en movimiento
rectilíneo uniforme
Presupone la existencia
de los SRI

9. Teoría de la
Relatividad de Galileo
Teoría Especial de
la Relatividad
Válida la primera ley de
Newton o Principio de la
Inercia SRI

10. Masa [kg]
• Es la magnitud física que permite
cuantificar la inercia
• La masa de un cuerpo es una medida de
su inercia
• La masa es una medida de la oposición
de un cuerpo a cambiar su estado de
movimiento
Es un escalar positivo o nulo m ≥ 0

11. Cantidad de Movimiento lineal
de una partícula
Se define como el producto de la masa
por la velocidad de la partícula.
p = mV
V p
[kg m/s]
Tiene carácter vectorial, y como m es
un escalar, entonces p V

12. Realidad Realidad
reflejada por un reflejada por un
observador en un observador en
SRI S otro SRI S´
Dejando invariante la forma de las
leyes físicas

13. m0
La masa es un
Teoría de la m = γ m′
invariante
Relatividad de Galileo
relativista
m0
m=
Teoría Especial de m = m′ V2
1− 2
c
la Relatividad
m ≥m0
Al considerar la cantidad de
m p
movimiento lineal como el
producto de la masa (relativista) p = mV
Si se cumple la ley de conservación de la cantidad
por la velocidad, entonces, si p del
de movimiento lineal SRI, un SRI, entonces se
sistema se conserva en un para
incumple para otro SRI´ que se mueva respecto al
también se conservará en
m0 cualquier otro SRI,
primero a v grandes p = m0V
independientemente deV la Mec. de Newton
velocidad del observador.
c 1 V/c

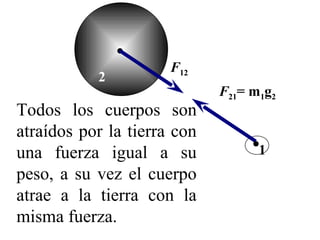
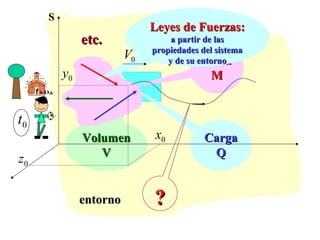
14. FUERZA de interacción [N]
Es la magnitud física que permite
cuantificar la acción del entorno
material sobre el sistema bajo estudio.
Esta acción depende de las
propiedades del sistema y del entorno
y en algunos casos del estado del
movimiento del sistema.
Tiene carácter vectorial F

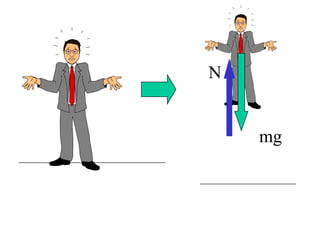
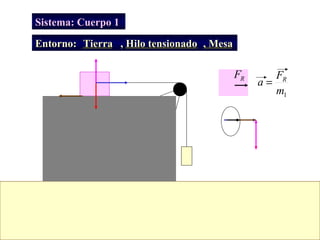
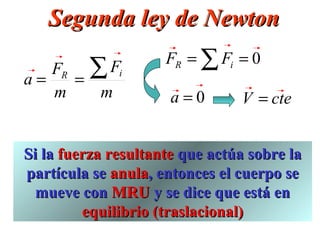
15. Segunda ley de Newton
entorno
F1 FR
F3
cuerpo
F1 F2 F3
F2
FR
a FR = m a
[N=kg m/s2]
La fuerza resultante que actúa sobre el
cuerpo es igual al producto de la masa del
cuerpo por la aceleración que adquiere.

16. Sistema: Cuerpo 1
Entorno: Tierra , Hilo tensionado , Mesa
FR FR
a=
m1

17. Segunda ley de Newton
F R = F 1 + F 2 + F3 + F 4
F1 F2
FR ∑ Fi
a= =
m m
F4 F3
∑F ix = ma x ∑F iy = ma y ∑F
iz = ma z
La aceleración del cuerpo es directamente
proporcional a la fuerza resultante que
actúa sobre él e inversamente
proporcional a su masa.

18. Segunda ley de Newton
FR = ∑ Fi = 0
FR ∑ Fi
a= =
m m a=0 V = cte
Si la fuerza resultante que actúa sobre la
partícula se anula, entonces el cuerpo se
mueve con MRU y se dice que está en
equilibrio (traslacional)

19. Teoría de la
Válida la segunda ley
Relatividad de Galileo
de Newton
Teoría Especial de F = ma
la Relatividad
m = m0 = cte
independiente del observador
dp d ( mv )
FR = FR = =ma
dt dt
v << c

20. Teoría de la
Válida la segunda ley
Relatividad de Galileo
de Newton
Teoría Especial de F = ma
la Relatividad
m = m0 = cte
Aún tomando a m nte della masa
independie como observador
relativista, la expresión F = ma cambia
de forma al llevarla de un sistema de
SRI a otro, incluso a través de las
transformaciones de Lorentz

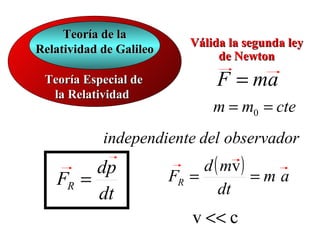
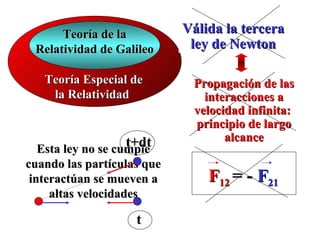
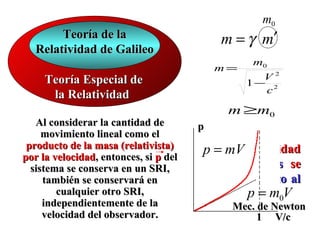
21. Teoría de la Válida la segunda ley
Relatividad de Galileo de Newton
Teoría Especial de d ( mv )
dp
F= = m0 a
la Relatividad F=dt
v <<dt
c
FUERZA [N]
Si en un SRI una partícula cambia su cantidad de
movimiento lineal, entonces existe una causa que provoca
este cambio: la acción de una fuerza sobre dicha
partícula, la cual es igual al cambio de la cantidad de
movimiento en el tiempo. Esta expresión es válida para
cualquier SRI, independientemente de la velocidad del
observador.

22. Tercera ley de Newton
Las fuerzas con que dos cuerpos actúan
uno sobre otro, son siempre de igual
módulo, están en la misma dirección y en
sentido contrario.
Agente externo 1
2
F12 = - F21
Esta ley sugiere que las fuerzas de interacción surgen
siempre por pares. Están aplicadas en cuerpos
diferentes

23. T
S

24. F12
2
F21= m1g2
Todos los cuerpos son
atraídos por la tierra con
una fuerza igual a su 1
peso, a su vez el cuerpo
atrae a la tierra con la
misma fuerza.

25. Teoría de la Válida la tercera
Relatividad de Galileo ley de Newton
Teoría Especial de Propagación de las
la Relatividad interacciones a
velocidad infinita:
principio de largo
t+dt alcance
Esta ley no se cumple
cuando las partículas que
interactúan se mueven a F12 = - F21
altas velocidades
t

26. N
mg

27. El DCL de los cuerpos será:

28. N1 N2
mg N1
Mg
N2
mg Mg

29. Diagrama de fuerzas

30. Ejemplos
1. Si sobre un cuerpo de 10 kg de masa actúan las
fuerzas: F1=100 i + 30j, F2= -30 i – 40 j y
F3= -110 i - 20j, determine la aceleración que
adquiere m.
2. Las coordenadas de posición de una partícula de 5
kg están dadas según:
x(t) = 2t2 – t + 5 y y(t) = t3 –2t2 –t +2.
Determine a) la fuerza que actúa sobre ella en el
instante t = 2s, b) su at y aN en t = 2s, c) el ángulo
que forma la velocidad con la aceleración en el
instante t = 2s.

31. 4. En el sistema mostrado determinese
la tensión de los cables si el sistema se
encuentra en equilibrio
53 37
m m = 10kg

32. 6. El bloque resbala sin fricción con velocidad
constante v = 2,5 m/s sobre el plano inclinado. La
polea es ideal. Determine:
a) el DCL de m
b) La tensión del cable
c) Si a mitad de camino se rompe el cable, halle la
aceleración con la cual cae el bloque.
37o