Subido porDiegoFernndezVillar
817 vistas

Libro Matematicas 2ºEV 4ºPrimaria

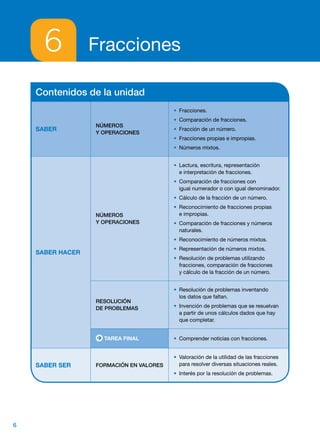
Este documento presenta una guía didáctica para la asignatura de matemáticas del cuarto curso de primaria. La guía fue creada por un equipo de Santillana Educación y contiene 15 unidades sobre diferentes temas matemáticos, así como ejercicios de cálculo mental, resolución de problemas y habilidades prácticas.

Incrustar presentación

Descargar para leer sin conexión
PRIMARIA Matemáticas GUÍA DIDÁCTICA BIBLIOTECA DEL PROFESORADO La guía didáctica Matemáticas 4, para cuarto curso de Primaria, es una obra colectiva concebida, diseñada y creada en el Departamento de Ediciones Educativas de Santillana Educación, S. L., dirigido por Teresa Grence Ruiz. En su elaboración ha participado el siguiente equipo: TEXTO Y EDICIÓN José Antonio Almodóvar Herráiz Pilar García Atance ILUSTRACIÓN Irene Hervás Alonso Felipe López Salán Eduardo Leal Uguina EDICIÓN EJECUTIVA José Antonio Almodóvar Herráiz DIRECCIÓN DEL PROYECTO Domingo Sánchez Figueroa DIRECCIÓN Y COORDINACIÓN EDITORIAL DE PRIMARIA Maite López-Sáez Rodríguez-Piñero
Dirección de arte: José Crespo Proyecto gráfico: Estudio Pep Carrió Fotografía de la cubierta: Leila Méndez Jefa de proyecto: Rosa Marín Coordinación de ilustración: Carlos Aguilera Jefe de desarrollo de proyecto: Javier Tejeda Desarrollo gráfico: Jorge Gómez, Raúl de Andrés Dirección técnica: Jorge Mira Subdirección técnica: José Luis Verdasco Coordinación técnica: Alejandro Retana Confección y montaje: Hilario Simón, Raquel Sánchez Corrección: Marta Rubio, Nuria del Peso Documentación y selección fotográfica: Nieves Marinas Fotografías: J. Jaime; A. G. E. FOTOSTOCK/Fernando Fernández; GETTY IMAGES SALES SPAIN/Photos.com Plus; HIGHRES PRESS STOCK/AbleStock.com; STOCKBYTE; MATTON-BILD; SERIDEC PHOTOIMAGENES CD; ARCHIVO SANTILLANA Cualquier forma de reproducción, distribución, comunicación pública o transformación de esta obra solo puede ser realizada con la autorización de sus titulares, salvo excepción prevista por la ley. Diríjase a CEDRO (Centro Es- pañol de Derechos Reprográficos, www.cedro.org <http://www.cedro.org>) si necesita fotocopiar o escanear algún fragmento de esta obra. © 2015 by Santillana Educación, S. L. Avda. de los Artesanos, 6 28760 Tres Cantos, Madrid PRINTED IN SPAIN ISBN: 978-84-8305-567-0 CP: 664734 Depósito legal: M-24540-2015
Índice Mapa de contenidos...................................................  4 Guiones didácticos Unidad 6. Fracciones..................................................  6 Unidad 7. Números decimales.................................... 24 Unidad 8. Operaciones con números decimales........ 40 Unidad 9. Tiempo y dinero.......................................... 58 Unidad 10. Longitud.................................................... 74
Unidades Información y actividades 1 Números de hasta siete cifras 6 • Números de seis cifras • Aproximaciones • Números de siete cifras • Números romanos 2 Suma y resta 22 • Propiedades conmutativa y asociativa • Sumas y restas combinadas • Estimación de sumas y de restas 3 Multiplicación 36 • Multiplicación por números de varias cifras • Estimación de productos • Propiedades de la multiplicación Tratamiento de la información. Coordenadas de puntos en una cuadrícula 4 División 52 • División exacta y división entera • Divisiones con ceros en el cociente • Prueba de la división • Operaciones combinadas 5 Práctica de la división 66 • Divisiones con divisor de dos cifras (I) • Propiedad de la división exacta • Divisiones con divisor de dos cifras (II) REPASO TRIMESTRAL 6 Fracciones 82 • Fracciones. Comparación de fracciones • Fracciones propias e impropias • Fracción de un número • Números mixtos 7 Números decimales 98 • Unidades decimales • Comparación de decimales • Números decimales • Aproximación de decimales 8 Operaciones con números decimales 112 • Suma de números decimales • Multiplicación de números • Resta de números decimales decimales Tratamiento de la información. de barras de tres características 9 Tiempo y dinero 128 • El reloj digital • Problemas con tiempo y dinero • Unidades de tiempo 10 Longitud 142 • El metro, el decímetro y el centímetro • El kilómetro, el hectómetro • El milímetro y el decámetro REPASO TRIMESTRAL 11 Capacidad y masa 158 • El decilitro, el centilitro y el mililitro • El decagramo, el hectogramo • El decalitro, el hectolitro y el kilolitro y el kilogramo • El decigramo, el centigramo • Problemas de medida y el miligramo 12 Rectas y ángulos 172 • Recta, semirrecta y segmento • Simetrías y traslaciones • Medida y trazado de ángulos 13 Polígonos 186 • Perímetro. Polígonos regulares • de triángulos • de cuadriláteros y paralelogramos Tratamiento de la información. Pictogramas 14 Cuerpos geométricos 202 • Prismas y pirámides. Elementos • Cuerpos redondos • de prismas y pirámides 15 Probabilidad y estadística 216 • Suceso seguro, posible e imposible • Media • Más probable y menos probable REPASO TRIMESTRAL Unidades Información y actividades 1 Números de hasta siete cifras 6 • Números de seis cifras • Aproximaciones • Números de siete cifras • Números romanos 2 Suma y resta 22 • Propiedades conmutativa y asociativa • Sumas y restas combinadas • Estimación de sumas y de restas 3 Multiplicación 36 • Multiplicación por números de varias cifras • Estimación de productos • Propiedades de la multiplicación Tratamiento de la información. Coordenadas de puntos en una cuadrícula 4 División 52 • División exacta y división entera • Divisiones con ceros en el cociente • Prueba de la división • Operaciones combinadas 5 Práctica de la división 66 • Divisiones con divisor de dos cifras (I) • Propiedad de la división exacta • Divisiones con divisor de dos cifras (II) REPASO TRIMESTRAL 6 Fracciones 82 • Fracciones. Comparación de fracciones • Fracciones propias e impropias • Fracción de un número • Números mixtos 7 Números decimales 98 • Unidades decimales • Comparación de decimales • Números decimales • Aproximación de decimales 8 Operaciones con números decimales 112 • Suma de números decimales • Multiplicación de números • Resta de números decimales decimales Tratamiento de la información. de barras de tres características 9 Tiempo y dinero 128 • El reloj digital • Problemas con tiempo y dinero • Unidades de tiempo 10 Longitud 142 • El metro, el decímetro y el centímetro • El kilómetro, el hectómetro • El milímetro y el decámetro REPASO TRIMESTRAL 11 Capacidad y masa 158 • El decilitro, el centilitro y el mililitro • El decagramo, el hectogramo • El decalitro, el hectolitro y el kilolitro y el kilogramo • El decigramo, el centigramo • Problemas de medida y el miligramo 12 Rectas y ángulos 172 • Recta, semirrecta y segmento • Simetrías y traslaciones • Medida y trazado de ángulos 13 Polígonos 186 • Perímetro. Polígonos regulares • de triángulos • de cuadriláteros y paralelogramos Tratamiento de la información. Pictogramas 14 Cuerpos geométricos 202 • Prismas y pirámides. Elementos • Cuerpos redondos • de prismas y pirámides 15 Probabilidad y estadística 216 • Suceso seguro, posible e imposible • Media • Más probable y menos probable REPASO TRIMESTRAL
Cálculo mental Solución de problemas Saber hacer • Sumar decenas, centenas y millares • Restar decenas, centenas y millares • Pasos para resolver un problema • Analizar datos de estadios • Sumar decenas a números de 3 y de 4 cifras • Restar decenas a números de 3 y de 4 cifras • Completar enunciados • Elegir regalos con puntos • Sumar centenas a números de 3 y de 4 cifras • Restar centenas a números de 3 y de 4 cifras • Reconstruir el enunciado • Comprobar un pedido • Multiplicar un número por 10, 100 y 1.000 • Multiplicar un dígito por decenas, centenas y millares • Sacar conclusiones de un enunciado • Conocer las reglas de un juego • Multiplicar dos números terminados en cero • Multiplicar números de 2 cifras por 2 y por 20 • Averiguar los datos que sobran e inventar preguntas • Organizar grupos • Dividir decenas, centenas y millares entre 10 • Dividir centenas y millares entre 100 y entre 1.000 • Averiguar e inventar los datos que faltan • Comprender noticias con fracciones • Hallar la mitad de decenas y de centenas • Hallar la mitad de números de 2 y de 3 cifras • Ordenar los datos de un problema • Estudiar la evolución de un precio • Sumar 11 a un número • Sumar 9 a un número • Extraer datos de la resolución de un problema • Revisar una factura • Restar 11 a un número • Restar 9 a un número • Cambiar datos para obtener una solución distinta • Programar horarios • Sumar números de 2 cifras sin llevar • Sumar números de 2 cifras llevando • Elegir la pregunta para que el problema se resuelva con dos operaciones • Interpretar datos de altitudes • Sumar 21, 31, 41... a números de 2 cifras • Sumar 19, 29, 39... a números de 2 cifras • Elegir la pregunta que se responde con unos cálculos • Realizar cálculos en un laboratorio • Restar 21, 31, 41... a números de 2 cifras • Restar 19, 29, 39... a números de 2 cifras • Elegir las preguntas que se pueden responder a partir del enunciado • Trabajar con ángulos en los deportes • Sumar 101, 201... a números de 3 cifras • Sumar 99, 199... a números de 3 cifras • Escribir las cuestiones intermedias en problemas de dos o más operaciones • Analizar mosaicos • Multiplicar por 11 números de 2 cifras • Multiplicar por 101 números de 2 cifras • Elegir los cálculos que resuelven un problema • Interpretar una maqueta • Multiplicar por 5 números de 2 cifras • Multiplicar por 50 números de 2 cifras • Elegir la solución más razonable • Elegir la estrategia en un concurso Cálculo mental Solución de problemas Saber hacer • Sumar decenas, centenas y millares • Restar decenas, centenas y millares • Pasos para resolver un problema • Analizar datos de estadios • Sumar decenas a números de 3 y de 4 cifras • Restar decenas a números de 3 y de 4 cifras • Completar enunciados • Elegir regalos con puntos • Sumar centenas a números de 3 y de 4 cifras • Restar centenas a números de 3 y de 4 cifras • Reconstruir el enunciado • Comprobar un pedido • Multiplicar un número por 10, 100 y 1.000 • Multiplicar un dígito por decenas, centenas y millares • Sacar conclusiones de un enunciado • Conocer las reglas de un juego • Multiplicar dos números terminados en cero • Multiplicar números de 2 cifras por 2 y por 20 • Averiguar los datos que sobran e inventar preguntas • Organizar grupos • Dividir decenas, centenas y millares entre 10 • Dividir centenas y millares entre 100 y entre 1.000 • Averiguar e inventar los datos que faltan • Comprender noticias con fracciones • Hallar la mitad de decenas y de centenas • Hallar la mitad de números de 2 y de 3 cifras • Ordenar los datos de un problema • Estudiar la evolución de un precio • Sumar 11 a un número • Sumar 9 a un número • Extraer datos de la resolución de un problema • Revisar una factura • Restar 11 a un número • Restar 9 a un número • Cambiar datos para obtener una solución distinta • Programar horarios • Sumar números de 2 cifras sin llevar • Sumar números de 2 cifras llevando • Elegir la pregunta para que el problema se resuelva con dos operaciones • Interpretar datos de altitudes • Sumar 21, 31, 41... a números de 2 cifras • Sumar 19, 29, 39... a números de 2 cifras • Elegir la pregunta que se responde con unos cálculos • Realizar cálculos en un laboratorio • Restar 21, 31, 41... a números de 2 cifras • Restar 19, 29, 39... a números de 2 cifras • Elegir las preguntas que se pueden responder a partir del enunciado • Trabajar con ángulos en los deportes • Sumar 101, 201... a números de 3 cifras • Sumar 99, 199... a números de 3 cifras • Escribir las cuestiones intermedias en problemas de dos o más operaciones • Analizar mosaicos • Multiplicar por 11 números de 2 cifras • Multiplicar por 101 números de 2 cifras • Elegir los cálculos que resuelven un problema • Interpretar una maqueta • Multiplicar por 5 números de 2 cifras • Multiplicar por 50 números de 2 cifras • Elegir la solución más razonable • Elegir la estrategia en un concurso
Fracciones6 Contenidos de la unidad SABER NÚMEROS Y OPERACIONES • Fracciones. • Comparación de fracciones. • Fracción de un número. • Fracciones propias e impropias. • Números mixtos. SABER HACER NÚMEROS Y OPERACIONES • Lectura, escritura, representación e interpretación de fracciones. • Comparación de fracciones con igual numerador o con igual denominador. • Cálculo de la fracción de un número. • Reconocimiento de fracciones propias e impropias. • Comparación de fracciones y números naturales. • Reconocimiento de números mixtos. • Representación de números mixtos. • Resolución de problemas utilizando fracciones, comparación de fracciones y cálculo de la fracción de un número. RESOLUCIÓN DE PROBLEMAS • Resolución de problemas inventando los datos que faltan. • Invención de problemas que se resuelvan a partir de unos cálculos dados que hay que completar.   TAREA FINAL • Comprender noticias con fracciones. SABER SER FORMACIÓN EN VALORES • Valoración de la utilidad de las fracciones para resolver diversas situaciones reales. • Interés por la resolución de problemas. 6
BIBLIOTECA DEL PROFESORADO Programación didáctica de aula Recursos para la evaluación • Evaluación de contenidos. Unidad 6: pruebas de control B y A. • Evaluación por competencias. Prueba 6. •  Rúbrica. Unidad 6. Enseñanza individualizada • Plan de mejora. Unidad 6. • Programa de ampliación. Unidad 6. Proyectos de trabajo cooperativo • Proyecto del segundo trimestre. Recursos complementarios • Fichas para el desarrollo de la inteligencia. • Operaciones y problemas. Aprendizaje eficaz • Técnicas de estudio y presentación de exámenes. Proyectos interdisciplinares • Programa de Educación en valores. • Programa de Educación emocional. •  Inteligencias múltiples. RECURSOS DIGITALES LibroMedia • Unidad 6: actividades y recursos. MATERIAL DE AULA Láminas OTROS MATERIALES DEL PROYECTO Cuaderno del alumno • Segundo trimestre. Unidad 6. Solución de problemas. Método DECA ES0000000024590 663006_Matematicas_4_GRAZ_24259 PRIMARIA PRIMARIA Matemáticas PRIMARIA ANDALUCÍAMatemáticas ANDALUCÍA Matemáticas ANDALUCÍA ES0000 000024 590 663006 _Matem aticas_4_GRA Z_2425 9.indd 1 04/03/2 015 11:21:19 ES0000000024593 663039_Cdno_Matematicas_4-2_22732 PRIMARIA Matemáticas Segundo trimestre Matemáticas Segundo trimestre PRIMARIA CUADERNO CUADERNO ES0000000024593 663039_Cdno_Matematicas_4-2_22732.indd 1 19/02/2015 16:56:18 SUGERENCIA DE TEMPORALIZACIÓN Enero MarzoFebrero 7
6 Fracciones Limpiando el bosque Otro año más, los vecinos de Villares se reúnen para ir a los montes cercanos y limpiarlos. Personas de todas las edades colaboran ese día. Entre los pequeños esta iniciativa es cada vez más popular y cada año se apuntan más. En muy poco tiempo se limpia todo el monte y se deja preparado para poder disfrutarlo. Limpiadores por edades cada año Niños Adultos Mayores 2013 2014 82 ES0000000024590 663006-Unidad 06_22589.indd 82 10/03/2015 13:16:43 Limpiadores por edades cada año Niños Adultos Mayores 2013 2014 Propósitos •  Reconocer situaciones reales   en las que para su resolución   se utilizan las fracciones. •  Recordar los conceptos básicos necesarios para el desarrollo   de la unidad. Previsión de dificultades •  Aunque los alumnos resuelvan bien las actividades, pueden hacerlo   de forma mecánica, sin comprender el concepto de fracción. Pregúnteles a menudo qué significa cada término de la fracción. •  Puede resultarles complejo   el calcular la fracción de un número y aplicarlo en la resolución de problemas. Trabaje el proceso   de forma colectiva, pidiendo a los alumnos que expliquen los pasos realizados. •  Para evitar errores de comprensión con los números mixtos muestre siempre su equivalencia con la suma de cierto número de unidades completas y una fracción propia. Trabajo colectivo sobre la lámina Lea la lectura y pregunte a los alumnos su opinión acerca de   la limpieza de los bosques, por qué creen que es importante limpiarlos, etc. A continuación pídales que observen el gráfico y realice de forma colectiva la primera cuestión para comprobar que los alumnos   lo interpretan correctamente. 1   El gráfico de 2013 tiene 5 partes.   Una parte corresponde a los niños, dos a los adultos   y una a los mayores. 2   En 2014 los niños fueron dos partes.  Hubo más niños que en 2013,   ya que 2 1. Otras formas de empezar •  Lleve a la clase algunas piezas de fruta, por ejemplo, una manzana, una pera, un melocotón, una mandarina, etc. Divida, a la vista de los alumnos, cada pieza de fruta en varios trozos iguales o la mandarina en gajos. Por turno, los alumnos elegirán una fruta, cogerán algunos de sus trozos   y le dirán cuántos trozos (o gajos) hay de esa fruta y cuántos han cogido, siguiendo este modelo: «Hay … trozos de … y he cogido … trozos».   Pídales después que escriban la fracción asociada en la pizarra. 8
¿Qué sabes ya? 1 El gráfico de 2013, ¿cuántas partes tiene? ¿Cuántas corresponden a los niños? ¿Cuántas partes corresponden a los adultos? ¿Y cuántas a los mayores? 2 ¿Qué parte de los limpiadores fueron niños en 2014? ¿Hubo mayor o menor número de niños limpiadores que en 2013? ¿Por qué? 3 EXPRESIÓN ORAL. Explica si el número de limpiadores adultos aumentó o disminuyó de 2013 a 2014. Lee, comprende y razona TAREA FINAL Comprender noticias con fracciones Entenderás noticias con fracciones. Antes, aprenderás a interpretarlas, escribirlas y compararlas, y a calcular la fracción de un número. SABER HACER La mitad de un número Para calcular la mitad de un número, divide ese número entre 2. La mitad de 16 16 : 2 5 8 La mitad de 40 40 : 2 5 20 La mitad de una figura Cada figura está dividida en dos partes iguales. La mitad de cada figura es de color rojo. 1 Calcula la mitad de cada número. 8 16 42 180 642 2.364 2 Escribe en tu cuaderno en qué figuras se ha coloreado la mitad. a. b. c. d. 83 ES0000000024590 663006-Unidad 06_22589.indd 83 10/03/2015 13:16:44 UNIDAD 6 3 En 2014 los adultos fueron dos partes del total de limpiadores, mientras que en 2013 fueron tres partes. El número de adultos disminuyó. ¿Qué sabes ya? Recuerde con los alumnos el procedimiento para calcular la mitad de un número y también el concepto de mitad de una figura geométrica. Señale que, para determinar la mitad en este último caso, hay que analizar si todas las partes son iguales, contar el número total de ellas y cuántas están coloreadas. 1 •  4 •  8 •  21 •  90 •  321 •  1.182 2 Figuras a, c y d. Notas Competencias •  Comunicación lingüística. Al realizar las actividades propuestas después de la lectura, es importante que los alumnos utilicen correctamente el lenguaje matemático para expresarse. Compruebe, sobre todo, en la de Expresión oral que lo hacen de forma clara. •  Aprender a aprender. Señale a los alumnos la importancia de afianzar los conocimientos para poder avanzar. Recuérdeles que ya en el curso pasado estudiaron las fracciones y el significado de sus términos, e indique que van a seguir aprendiendo más cosas sobre ellas. Inteligencia lingüística 9
Fracciones: lectura y escritura 1 Copia las figuras y escribe la fracción que representa la parte coloreada. 2 Copia las figuras y colorea en cada una la fracción que se indica. 3 Copia la figura y colorea. Observa la parte de la figura que ha coloreado cada niño. Esta figura está dividida en 2 partes iguales. Hay 1 parte coloreada. Para expresarlo utilizamos esta fracción: 1 2 . Numerador. Número de partes coloreadas Denominador. Número de partes iguales de la figura Esta figura está dividida en 3 partes iguales. Hay 1 parte coloreada. Para expresarlo utilizamos esta fracción: 1 3 . Numerador. Número de partes coloreadas Denominador. Número de partes iguales de la figura 1 3 1 2 1 3 1 2 2 4 3 5 2 9 4 9 3 9 84 ES0000000024590 663006-Unidad 06_22589.indd 84 10/03/2015 13:16:46 Propósitos •  Leer y escribir fracciones. •  Reconocer los términos   de una fracción. •  Resolver problemas con fracciones. Sugerencias didácticas Para explicar. Lea la situación y,   con el apoyo de la ilustración, indique cómo se escribe la fracción correspondiente a cada figura   coloreada y el significado de cada término. Después, exprese cómo   se lee esta fracción y explique,   con la ayuda del cuadro del apartado Hazlo así, cómo se leen las fracciones cuyo denominador es un número menor o igual que 10. Deje claro que para poder hablar de fracciones debe cumplirse que todas las partes en las que está dividido el total son iguales. Para reforzar. Si lo cree conveniente, puede escribir en la pizarra (con cifras o con letras) distintas fracciones para que los alumnos las escriban de la otra forma y anoten también cuál es su numerador y denominador. Actividades 1 1 2     2 3     2 4     4 6 2 3 4 • Un tercio. •  Un cuarto. •  Dos quintos. •  Dos sextos. •  Cuatro séptimos. •  Tres octavos. •  Cinco novenos. Otras actividades •  Escriba en la pizarra varias fracciones y pida a los alumnos   que las representen en su cuaderno. Por ejemplo: 1 2           2 3           3 4           4 5 Si tienen dificultades, puede sugerirles que, para cada fracción, tienen   que dibujar una figura (la más sencilla es un rectángulo de un cuadradito   de ancho) formada por tantos cuadraditos como indique el denominador de la fracción y colorear tantos cuadraditos como señale el numerador.   Lea después, de forma colectiva, las fracciones y comente algunas   de las representaciones aportadas. 10
6 Divide decenas, centenas, millares y decenas de millar entre 10 40 : 10 300 : 10 7.000 : 10 20.000 : 10 80 : 10 500 : 10 9.000 : 10 50.000 : 10 60 : 10 400 : 10 5.000 : 10 80.000 : 10 90 : 10 700 : 10 8.000 : 10 90.000 : 10 CÁLCULO MENTAL 30 : 10 5 3 500 : 10 5 50 4.000 : 10 5 400 30.000 : 10 5 3.000 4 Escribe en tu cuaderno cómo se lee cada fracción. 1 3 1 4 2 5 2 6 4 7 3 8 5 9 5 Escribe las fracciones. Dos cuartos. Tres quintos. Cuatro sextos. Tres séptimos. Siete octavos. Seis novenos. Problemas 6 Resuelve. Elena preparó para su cumpleaños estas 3 pizzas y dividió cada una en las partes que se indican: ¿Qué fracción representa un trozo de cada clase de pizza? Si de la pizza de queso se comieron siete octavos, ¿qué fracción de pizza quedó? HAZLO ASÍ 1 2 un medio 2 3 dos tercios 3 4 tres cuartos 4 5 cuatro quintos 1 6 un sexto 3 7 tres séptimos 5 8 cinco octavos 7 9 siete novenos ATÚN QUESO JAMÓN 85 ES0000000024590 663006-Unidad 06_22589.indd 85 10/03/2015 13:16:48 UNIDAD 6 5 •  2 4 •  3 5 •  4 6 •  3 7 •  7 8 •  6 9 6 •  Atún: 1 4 . Queso: 1 8 . Jamón: 1 6 . •  Quedó 1 8 . Cálculo mental • 4 •  30 •  700 •  2.000 •  8 •  50 •  900 •  5.000 •  6 •  40 •  500 •  8.000 •  9 •  70 •  800 •  9.000 Notas Otras actividades •  Puede también trabajar el concepto de fracción de un conjunto (parte de elementos de un conjunto que cumplen una cierta condición).   Saque a la pizarra a un grupo de como máximo 10 alumnos y pida a la clase que digan la fracción que expresa el número de alumnos que cumplen una determinada condición. Por ejemplo: – La fracción de niñas (o de niños) que hay en el grupo. – La fracción de alumnos del grupo que llevan pantalón. – La fracción de alumnos que llevan una prenda de color… Puede repetir la actividad variando el número de personas que forman el grupo, o por equipos de distinto número de miembros, para trabajar distintos denominadores. 11
Comparación de fracciones ¿En cuántas partes iguales está dividida cada figura? Figura a. … Figura b. … ¿Cuántas partes coloreadas tiene cada figura? Figura a. … Figura b. … ¿Qué fracción representa la parte coloreada de cada figura? ¿Cuál es la fracción mayor? ¿En cuántas partes iguales está dividida cada figura? Figura c. … Figura d. … ¿Cuántas partes coloreadas tiene cada figura? Figura c. … Figura d. … ¿Qué fracción representa la parte coloreada de cada figura? ¿Cuál es la fracción menor? ¿Qué ruleta tiene mayor zona roja? Fíjate en que la ruleta A tiene mayor zona roja que la ruleta B. Por tanto, resulta que: La fracción 5 8 es mayor que la fracción 3 8 . 5 8 . 3 8 ¿Qué ruleta tiene menor zona verde? Fíjate en que la ruleta D tiene menor zona verde que la ruleta C. Por tanto, resulta que: La fracción 1 8 es menor que la fracción 1 4 . 1 8 , 1 4 A CB D 5 8 1 4 3 8 1 8 1 Observa las figuras y contesta en tu cuaderno. a. c. b. d. 86 ES0000000024590 663006-Unidad 06_22589.indd 86 10/03/2015 13:16:49 Propósitos •  Comparar fracciones de igual denominador o numerador. •  Ordenar grupos de fracciones. Sugerencias didácticas Para explicar. Pida a los alumnos que observen en el libro la representación de las fracciones 5/8 y 3/8 y que comparen la parte roja. Señale que la primera figura tiene más parte coloreada que la segunda. Repita el proceso para las fracciones 1/4 y 1/8, de manera que los alumnos realicen la comparación de ambas fracciones de forma gráfica. Una vez realizada la actividad 1, donde se insiste en el trabajo gráfico, deje que los alumnos hagan por sí mismos la actividad 2 para que descubran el procedimiento de comparación a nivel numérico. Muestre la importancia de analizar siempre en primer lugar qué termino tienen en común las dos fracciones para después comparar el otro. Puede ser interesante realizar un mural en el que se ponga por escrito el procedimiento numérico con algún ejemplo. Para reforzar. Escriba varios grupos de fracciones con igual denominador o igual numerador para que los alumnos las ordenen de mayor a menor, o viceversa. Actividades 1 •  Figura a. 6 partes. Figura b. 6 partes. •  Figura a. 4 partes. Figura b. 2 partes. •  Figura a. 4 6 . Figura b. 2 6 . Fracción menor: 2 6 . •  Figura c. 6 partes. Figura d. 1 parte. •  Figura a. 1 parte. Figura b. 1 parte. Otras actividades •  Dibuje en la pizarra la siguiente figura y pida a los alumnos que la copien en sus cuadernos y coloreen el número de cuadrados que quieran. A continuación, agrupe a los alumnos por parejas y formule a cada pareja las siguientes preguntas: –  ¿Cuál de los dos ha coloreado más (o menos) parte de la figura? – ¿Qué fracción de la figura habéis coloreado cada uno? ¿Qué término coincide en ambas fracciones? – ¿Cuál de las dos fracciones tiene el numerador mayor (o menor)? ¿Cuál de las dos fracciones es mayor (o menor)? 12
Escribe tres fracciones más en cada serie y contesta. ¿Cuál es la fracción mayor en la serie a.? ¿Cuál es la fracción menor en la serie b.? RAZONAMIENTO Problemas 4 Resuelve. Marcos tiene dos cartulinas iguales, una roja y otra azul. Divide las dos en 8 partes iguales y utiliza 3 partes de cartulina roja y 5 partes de cartulina azul. ¿De qué color utiliza más? Nuria y Jorge tienen cada uno una ruleta de la misma forma y tamaño. La ruleta de Nuria está dividida en 9 partes iguales y la de Jorge en 8. Cada ruleta tiene 5 partes de rojo. ¿Qué ruleta tiene mayor zona de rojo? En una ciudad, tres séptimos de los productos reciclados son envases de vidrio, dos séptimos son envases de aluminio y un séptimo de plástico. ¿De qué tipo se recicla más? a. 1 2 , 1 3 , 1 4 b. 1 7 , 2 7 , 3 7 2 Copia y colorea en cada figura la fracción indicada. Después, completa en tu cuaderno. 3 Piensa y escribe las fracciones que se indican. Cuatro fracciones mayores que 2 7 y menores que 7 7 . Cuatro fracciones mayores que 1 9 y menores que 1 2 . 2 4 3 4 3 4 3 6 2 4 2 4 3 4 4 6 3 4 3 6 Las dos fracciones tienen igual el denominador. Compara los … Es menor la fracción de numerador menor. Las dos fracciones tienen igual el … Compara los … Es mayor la fracción de denominador menor. 6 87 ES0000000024590 663006-Unidad 06_22589.indd 87 17/03/2015 11:58:35 UNIDAD 6 •  Figura a. 1 6 . Figura b. 1 2 . Fracción menor: 1 6 . 2 Compara los numeradores. 2 4 , 3 4 Compara los denominadores. 3 4 . 3 6 3 •  3 7 , 4 7 , 5 7 , 6 7     •  1 8 , 1 7 , 1 6 , 1 5 4 • 3 8 , 5 8 . Utiliza más azul. •  5 9 , 5 8 . La ruleta de Jorge tiene más zona de color rojo. •  1 7 , 2 7 , 3 7 . Se reciclan más envases de vidrio. Razonamiento a.  1 5 , 1 6 , 1 7 b.  4 7 , 5 7 , 6 7 •  Fracción mayor: 1 2 . •  Fracción menor: 1 7 . Notas Otras actividades •  Dibuje en la pizarra tres rectángulos iguales divididos en 3, 4 y 6 partes iguales, respectivamente. Forme grupos de tres alumnos y pídales que cada uno copie las figuras y coloree dos partes en cada una. Después, pregúnteles: –  ¿Qué fracción habéis coloreado en cada figura? ¿Qué término coincide en las tres fracciones? –  ¿Cuál de las tres fracciones tiene el denominador menor (o mayor)? ¿Cuál de las tres fracciones es mayor (o menor)? 13
Fracción de un número 1 Calcula en tu cuaderno. 5 6 de 30 3 7 de 77 5 8 de 96 2 5 de 130 4 9 de 189 2 Contesta en tu cuaderno. ¿Cuántos centímetros son medio metro? 1 2 de 100 5 … ¿Cuántos gramos son un cuarto de kilo? ¿Cuántos minutos son 3 cuartos de hora? 3 Piensa y contesta sin calcular. ¿Qué es mayor: 4 5 de 20 o 2 5 de 20? ¿Qué es menor: 2 7 de 70 o 2 7 de 140? En la clase de 4.º hay 20 pinturas de cera. 3 4 de las pinturas son de color rojo. ¿Cuántas pinturas rojas hay? 3 4 de 20 5 15 Hay 15 pinturas rojas. Para calcular la fracción de un número: 1.º Divide el número entre el denominador de la fracción. 2.º Multiplica el cociente obtenido por el numerador de la fracción. Calcula 3 4 de 20 1.º Divide el número, 20, entre el denominador de la fracción, 4. 20 : 4 5 5 2.º Multiplica el cociente obtenido, 5, por el numerador de la fracción, 3. 5 3 3 5 15 EJEMPLO 5 6 de 30 30 : 6 5 …; … 3 5 5 … 5 6 de 30 5 … RECUERDA 1 metro 5 100 centímetros 1 kilogramo 5 1.000 gramos 1 hora 5 60 minutos 88 ES0000000024590 663006-Unidad 06_22589.indd 88 10/03/2015 13:16:52 Propósitos •  Calcular la fracción de un número. •  Resolver situaciones reales   en las que hay que calcular   la fracción de un número. Sugerencias didácticas Para explicar. Lea el problema propuesto y comente que en este caso calculamos la fracción de   un número, no de una figura. Explique los pasos a seguir, relacionándolo   con la idea de fracción vista hasta entonces: 3/4 de una unidad significa que de una unidad dividida en   4 partes iguales, cogemos 3 de las partes; de forma similar, para calcular 3/4 de 20 pinturas, dividimos 20 entre 4 y el resultado lo multiplicamos por 3. Si lo cree conveniente, puede trabajar con los alumnos este proceso manipulativamente. Haga en común la actividad 1  y ponga otros ejemplos para resolver de forma colectiva en la pizarra. Resuelva también entre todos   el primer problema, razonando   en común qué se debe calcular   y cómo se hace. Actividades 1 •  5 6 de 30 5 25 •  3 7 de 77 5 33 •  5 8 de 96 5 60 •  2 5 de 30 5 12 •  4 9 de 189 5 84 2 •  1 2 de 100 cm 5 50 cm •  1 4 de 1.000 g 5 250 g •  3 4 de 60 s 5 45 s 3 • 4 5 . 2 5 , luego 4 5 de 20 es mayor. •  70 , 140, luego 2 7 de 70   es menor. Otras actividades • Escriba en la pizarra varias fracciones de un número, para que los alumnos las copien y calculen en el cuaderno. Después, entregue a cada alumno un montoncito de garbanzos para que comprueben manipulativamente sus resultados siguiendo estos pasos: 1.º  Coger los garbanzos que indica el número. 2.º  Repartir los garbanzos en tantos grupos iguales como indica   el denominador de la fracción. 3.º  Contar los garbanzos que hay en el número de grupos que indica   el numerador de la fracción. 14
6 Problemas 4 Resuelve. En una bolsa hay 80 bombones. En un parque hay 160 bancos. 3 4 de los bombones son de fresa. 5 8 de los bancos son métalicos. ¿Cuántos bombones son de fresa? ¿Cuántos bancos no son metálicos? 5 Piensa y resuelve. En una clase hay 24 alumnos. De ellos, 2 8 vienen a clase caminando y 1 6 viene en autobús. ¿Cuántos alumnos de la clase vienen caminando? ¿Y en autobús? Hay 90 árboles frutales en el huerto. Un sexto de ellos son manzanos y tres quintos son perales. ¿Cuántos manzanos hay? ¿Y perales? En la biblioteca del colegio hay 250 libros. Tres quintos son cuentos, un décimo novelas y el resto son diccionarios. ¿Cuántos libros hay de cada tipo? Mónica tiene en su vivero 182 plantas. Dos séptimos son pinos y la mitad de los pinos son piñoneros. ¿Cuántos pinos piñoneros tiene? 6 Inventa y resuelve. Utiliza los datos 2 5 y 60 e inventa un problema. Después, resuélvelo y comprueba que lo has hecho bien. Divide centenas y millares entre 100 y entre 1.000 300 : 100 7.000 : 100 2.000 : 1.000 500 : 100 9.000 : 100 4.000 : 1.000 700 : 100 5.000 : 100 6.000 : 1.000 900 : 100 8.000 : 100 9.000 : 1.000 CÁLCULO MENTAL 900 : 100 5 9 6.000 : 100 5 60 7.000 : 1.000 5 7 60 2 5 89 ES0000000024590 663006-Unidad 06_22589.indd 89 10/03/2015 13:16:53 UNIDAD 6 4 •  3 4 de 80 5 80 Son de fresa 60. •  5 8 de 160 5 100 160 – 100 5 60 No son metálicos 60 bancos. 5 •  2 8 de 24 5 6; 1 6 de 24 5 4 Vienen caminando 6 alumnos y en autobús 4. •  1 6 de 90 5 15; 3 5 de 90 5 54 Hay 15 manzanos y 54 perales. •  3 5 de 250 5 150 1 10 de 250 5 25 250 2 (150 1 25) 5 75 Hay 150 cuentos, 25 novelas y 75 diccionarios. •  2 7 de 182 5 52; 1 2 de 52 5 26 Tiene 52 pinos y 26 de ellos son pinos piñoneros. 6 R. M. En un almacén hay 60 cajas. 2 5 de las cajas contienen balones. ¿Cuántas cajas con balones hay en el almacén? 2 5 de 60 5 24 En el almacén hay 24 cajas con balones. Cálculo mental •  3 •  70 •  2 •  5 •  90 •  4 •  7 •  50 •  6 •  9 •  80 •  9 Notas Otras actividades • Plantee de forma oral problemas similares a los propuestos en esta página del libro, para resolverlos en común. Por ejemplo: 2 Inés tiene 12 batidos. Un tercio de los batidos son de fresa, dos cuartos son de chocolate y un sexto son de vainilla. ¿Cuántos batidos tiene Inés de cada sabor? 2 Álvaro tiene un juego con 20 fichas. Un cuarto de las fichas son azules, dos quintos son rojas y el resto son verdes. ¿Cuántas fichas de cada color tiene el juego? 15
Fracciones propias e impropias 1 Fíjate en los términos de cada fracción y escribe en tu cuaderno si es mayor, menor o igual que la unidad. 5 6 10 8 6 6 7 5 4 4 8 9 13 10 2 Compara estas fracciones y números naturales. HAZLO ASÍ Compara 25 3 y 8 1.º Divide el numerador de la fracción entre el denominador y compara el cociente con el número natural. 2.º Si el cociente es menor, es mayor el número natural. En cualquier otro caso, es mayor la fracción. 12 2 5 3 23 3 13 5 3 6 17 2 19 4 4 Jon, Nicolás y Silvia están pintando cartulinas. ¿Qué fracción representa la parte pintada por cada uno? Jon Nicolás Silvia Ha pintado 4 6 . Ha pintado 6 6 5 1. Ha pintado 9 6 . La fracción 4 6 tiene el numerador menor que el denominador. Es una fracción propia y es menor que la unidad: 4 6 , 1. La fracción 6 6 tiene iguales su numerador y su denominador. Es igual a la unidad: 6 6 5 1. La fracción 9 6 tiene el numerador mayor que el denominador. Es una fracción impropia y es mayor que la unidad: 9 6 . 1. 8 5 8 25 3 . 8 2 5 3 1 8 90 Propósitos •  Reconocer fracciones propias   e impropias. •  Comparar fracciones y números naturales. Sugerencias didácticas Para explicar. Pida a los alumnos que lean la situación planteada   y se fijen en la parte de cartulina   que ha pintado cada uno. Caracterice las fracciones propias e impropias   y muestre la importancia de comparar siempre los dos términos para poder diferenciarlas. Trabaje en común el Hazlo así de la actividad 2, mostrando la técnica para comparar fracciones impropias y números naturales. Deje claro que toda fracción propia   es siempre menor que la unidad. Actividades 1 Mayores que la unidad: 10 8 , 7 5 y 13 10 . Iguales que la unidad: 6 6 y 4 4 . Menores que la unidad: 5 6 y 8 9 . 2 Conviene realizar el ejemplo resuelto en común, explicando que, para comparar una fracción   y un número natural, primero hay que calcular el cociente de la fracción y, después, comparar dicho cociente con el número natural. •  12 2 . 5 •  3 , 23 3 •  13 5 , 3 •  6 , 17 2 •  19 4 . 4 Notas Otras actividades •  Escriba en la pizarra varias fracciones en las que a cada una   le falte un término. Por ejemplo: 4               5               8               2             3             4 Elija una fracción en la que falte el numerador y propóngales que lo inventen para que la fracción sea mayor, menor e igual a la unidad. Después,   haga una puesta en común con los resultados. Proceda de forma análoga   con alguna fracción en la que falte el denominador. 16
96Números mixtos 1 Escribe el número mixto y la fracción que representa la parte coloreada. Fíjate en cuántas figuras completas hay. 2 Copia en tu cuaderno y representa cada número mixto. En la pizzería venden pizzas partidas en 8 trozos iguales. Miguel ha comprado 20 porciones para invitar a merendar a unos amigos. 20 8 de pizza son 2 pizzas y 4 8 de otra. 20 8 se escribe así: 2 4 8 . El número 2 4 8 es un número mixto y está formado por un número natural y una fracción. Un número mixto está formado por un número natural y una fracción. 2 pizzas Copia y rodea en tu cuaderno el número mixto mayor de cada pareja. RAZONAMIENTO 3 4 7 2 4 7 5 2 9 5 6 9 2 3 7 4 5 7 20 8 4 8 1 3 4 1 1 2 1 2 3 91 UNIDAD 6 Propósitos •  Reconocer un número mixto. •  Interpretar y representar números mixtos. Sugerencias didácticas Para explicar. Lea la situación propuesta y pida a los alumnos   que se fijen en la representación gráfica de las porciones de pizza. Muestre que 20 porciones son   2 pizzas completas y 4 porciones   de otra. Escriba en la pizarra   la fracción y el número mixto, haciéndoles ver la relación entre uno   y otro. Señale que todo número mixto está formado por un número natural (figuras enteras) y una fracción propia (partes de una figura). Actividades 1 1 2 3 5 5 3 2 2 5 5 12 5 1 2 4 5 6 4 2 Razonamiento Pida a los alumnos que expresen   sus ideas para resolver la actividad. Coméntelas señalando que una forma de resolverla es escribiendo cada número mixto en forma de fracción y comparando las fracciones obtenidas, o bien comparando las partes enteras de los números mixtos y si son iguales, las fracciones propias. 25 7 . 18 7     Es mayor 3 4 7 . 47 9 , 51 9     Es mayor 5 6 9 . 17 7 , 33 7     Es mayor 4 5 7 . Competencias •  Conciencia y expresión cultural. Las representaciones gráficas   son un componente fundamental a la hora de trabajar con fracciones   y números mixtos. Trabaje en común actividades similares a la actividad 2   en las que los alumnos tengan que realizar representaciones por sí mismos. Ayúdeles pidiéndoles que determinen en primer lugar, mirando el denominador de la fracción propia, en cuántas partes deben dividir cada unidad. Puede pedirles también que realicen dibujos utilizando representaciones   de números mixtos y que sus compañeros escriban qué números mixtos   se han utilizado. Inteligencia espacial 17
Averigua los datos que faltan en cada problema e invéntalos. Después, resuelve. 1 Marcos tiene 75 años, Luisa algunos menos que él y Teo menos que Luisa. ¿Cuántos años tienen entre los tres? 2 Laura tenía varias bolsas iguales de patatas. Vendió 35 kilos. ¿Cuántos kilos de patatas le sobraron? 3 César tenía varios billetes de 20 €. Prestó algunos a su hermana. ¿Cuánto dinero le quedó? 4 Marta es más alta que su hermana Paula. ¿Cuántos centímetros es más alta Marta que Paula? Vamos a leer el problema, averiguar los datos que faltan para resolverlo e inventar un valor para ellos. Después, lo resolveremos. Esta noche, en el restaurante, han pedido manzana de postre 14 personas, han pedido pera algunas personas menos y naranja algunas personas más. ¿Cuántas personas han pedido de postre fruta? 1.º Comprende. Datos Han pedido manzana 14 personas. Algunas personas menos han pedido pera, y algunas más han pedido naranja. Pregunta ¿Cuántas personas han pedido de postre fruta? Para resolver el problema hay que saber cuántas personas han pedido pera y cuántas naranja. Inventamos unos valores que cumplan el enunciado. Por ejemplo: han pedido pera 10 personas y naranja 20 personas. 2.º Piensa qué hay que hacer. Hay que sumar todas las personas que han pedido de postre fruta. 3.º Calcula. 14 1 10 1 20 5 44 Solución: Han pedido de postre fruta 44 personas. 4.º Comprueba. Revisa si lo has hecho bien. Averiguar e inventar los datos que faltan Solución de problemas 92 ES0000000024590 663006-Unidad 06_22589.indd 92 10/03/2015 13:16:58 Propósitos •  Resolver problemas averiguando   e inventando los datos que faltan. •  Completar unos cálculos e inventar problemas que se resuelvan   con dichos cálculos. Sugerencias didácticas Para explicar. Haga que los alumnos lean detenidamente el problema   y pregúnteles qué operación hay que realizar para resolverlo y qué datos hay que utilizar. Explique cuáles son los datos que faltan y muestre que se han inventado para esos datos unos valores que cumplen las condiciones del enunciado. Pídales que ellos mismos propongan otros valores posibles que cumplan también las condiciones, y que después resuelvan los problemas que hayan obtenido. Actividades 1 R. M. Marcos tiene 75 años, Luisa 5 años menos que él y Teo 5 años menos que Luisa. ¿Cuántos años tienen entre los tres?  75 1 70 1 65 5 210  Entre los tres tienen 210 años. 2 R. M. Laura tenía 9 bolsas   de patatas de 12 kg cada una.   Vendió 35 kilos. ¿Cuántos kilos  de patatas le sobraron?  12 3 9 2 35 5 73  Le sobraron 73 kg de patatas. 3 R. M. César tenía 7 billetes de 20 €. Prestó 2 billetes a su hermana. ¿Cuánto dinero le quedó?  7 3 20 2 2 3 20 5 100  Le quedaron 100 €. 4 R. M. Marta mide 135 cm   y su hermana Paula 116 cm. ¿Cuántos centímetros es más alta Marta que Paula?  135 2 116 5 19  Marta mide 19 cm más que Paula. 5 R. M. David compró 3 libros por   9 € cada uno y una bufanda   por 12 €. ¿Cuánto dinero gastó David?  3 3 9 1 12 5 39  David gastó 39 €. Otras actividades •  Agrupe a los alumnos por parejas e indique a cada alumno que   le diga a su compañero dos cálculos sencillos (hechos mentalmente),  para que este los escriba en una hoja e invente el enunciado de un problema, que se resuelva con dichos cálculos. A continuación, entre los dos resolverán el problema inventado comprobando si realizan los dos cálculos   propuestos al principio. 18
Inventa y completa en tu cuaderno los números que faltan en los cálculos. Después, escribe un problema que se resuelva con ellos. 6 Inventa los datos que faltan en cada problema. Fíjate después si tiene sentido y resuélvelo en tu cuaderno. 5 David compró varios libros, todos del mismo precio. Después, se compró una bufanda que era algo más cara que un libro. ¿Cuánto dinero gastó David? 6 Un perro grande pesa bastantes kilos. Un gato pesa mucho menos que él y un perro pequeño pesa casi igual que un gato. ¿Cuánto pesan los tres juntos? 7 En un vagón de tren iban varias personas. Al llegar a una parada, se bajaron algunas y subieron más personas de las que se bajaron. ¿Cuántas personas iban en el tren tras esa parada? 8 Marta compró varias cajas iguales de bombones. Jacinto compró el doble de bombones que ella. ¿Cuántos bombones compró Jacinto? 9 Ramón tenía unos ahorros. Su madre le dio un billete y después se compró un chándal. ¿Cuánto dinero le quedó? INVENTA TUS PROBLEMAS Inventa y completa en tu cuaderno los números que faltan en los cálculos. Después, escribe un problema que se resuelva con ellos. 70 1 ... 5 ... ... 1 10 5 ... 1 50 2 ... 5 ... ... 1 40 5 ... 3 6 3 ... 5 ... ... 1 8 5 ... 2 4 3 ... 5 ... 2 3 ... 5 ... 4 93 ES0000000024590 663006-Unidad 06_22589.indd 93 10/03/2015 13:17:00 UNIDAD 6 6   R. M. Un perro grande pesa 19 kg. Un gato pesa 2 kg y un perro pequeño pesa 3 kg. ¿Cuánto pesan los tres juntos? 19 1 2 1 3 5 24 Los tres juntos pesan 24 kg. 7   R. M. En un vagón de tren iban 45 personas. Al llegar a una parada se bajaron 17 personas y subieron 23. ¿Cuántas personas iban en el tren tras esa parada? 45 2 17 1 23 5 51 En el tren iban 51 personas. 8   R. M. Marta compró 3 cajas de bombones con 24 bombones cada una. Jacinto compró el doble de bombones que ella. ¿Cuántos bombones compró Jacinto? 3 3 24 3 2 5 144 Jacinto compró 144 bombones. 9   R. M. Ramón tenía ahorrados 85 €. Su madre le dio un billete de 20 € y después se compró un chándal por 59 €. ¿Cuánto dinero le quedó? 85 1 20 2 59 5 46 Le quedaron 46 €. Inventa tus problemas Realice el primer problema en común. Pida a un alumno que salga a la pizarra y exponga al resto de la clase su propuesta para completar los cálculos y un problema asociado. Entre todos se comprobará si la propuesta es o no correcta. Después, haga que realicen el resto de los problemas de forma individual y compruebe los resultados en común. 1   R. M. 70 1 40 5 110 110 1 10 5 120 Felipe tiene en su granja 70 corderos y 40 gallinas. Hoy ha comprado 10 corderos más. ¿Cuántos animales en total tiene ahora Felipe? 2   R. L. 3   R. L. 4   R. L. Competencias •  Iniciativa y emprendimiento. Las actividades de invención de problemas son un contexto muy adecuado para desarrollar esta competencia. Pida a los alumnos, a la hora de trabajar las actividades de esta página, que tengan cuidado al completar los cálculos y anímelos a ser creativos cuando planteen los problemas. Recuérdeles la importancia de comprobar que el problema que han planteado se resuelve con dichos cálculos. Inteligencia intrapersonal 19
6 Completa los huecos. 3 7 , 7 4 8 . 4 6 . 6 10 , 10 7 Calcula. 3 8 de 16 3 8 de 88 9 10 de 500 6 7 de 147 2 3 de 2.340 4 5 de 6.925 8 VOCABULARIO. Explica qué son las fracciones impropias y cómo puedes reconocerlas. 9 Escribe en tu cuaderno, para cada fracción, si es mayor, menor o igual que la unidad. 9 9 7 4 4 7 8 9 6 2 10 Compara. Escribe el signo adecuado. 11 2 y 4 3 y 8 3 17 5 y 2 5 y 22 4 11 Escribe el número mixto y la fracción representados en cada figura. 12 Escribe un número mixto y represéntalo en tu cuaderno. 1 Escribe la fracción que representa la parte coloreada e indica cuáles son sus términos. 2 Escribe cómo se lee cada fracción. 3 7 1 2 2 4 4 5 5 6 3 8 7 9 9 10 3 Expresa con cifras. Un quinto. Cuatro octavos. Dos sextos. Un tercio. Cinco décimos. Tres cuartos. Tres novenos. Dos séptimos. 4 Copia y colorea para que la descripción sea cierta. Seis décimos de los globos son azules y el resto son rojos. 5 Compara. 5 6 5 7 6 10 3 10 5 8 3 8 4 9 4 5 ACTIVIDADES 94 ES0000000024590 663006-Unidad 06_22589.indd 94 10/03/2015 13:17:01 Propósitos •  Repasar y afianzar los contenidos básicos de la unidad. Actividades 1   5 8 ; 6 10 ; 4 9 ; 4 5 2   •  Tres séptimos. •  Un medio. •  Dos cuartos. •  Cuatro quintos. •  Cinco sextos. •  Tres octavos. •  Siete novenos. •  Nueve décimos. 3   •  1 5 •  2 6 •  15 10 •  3 9 •  4 8 •  1 3 •  3 4 •  2 7   4   6 10 de 10 5 6 Rojos: 6, azules: 4. 5   •  5 6 . 5 7 •  6 10 . 3 10 •  5 8 . 3 8 •  4 9 , 4 5 6   R. M. •  3 7 , 5 7 •  4 8 . 4 10 •  6 8 . 6 9 •  4 10 , 7 10 7   •  6 •  33 •  450 •  126 •  1.560 •  5.540 8   Las fracciones impropias son mayores que la unidad y tienen el numerador mayor que el denominador. 9  Mayores: 7 4 y 6 2 . Igual: 9 9 . Menores: 4 7 y 8 9 . 10  •  11 2 . 4 •  3 . 8 3 •  17 5 . 2 •  5 , 22 4 11  • 1 3 6 5 9 6 •  2 1 2 5 5 2 Otras actividades •  Nombre varias fracciones para que los alumnos las escriban en el cuaderno al dictado. Por ejemplo: 1 2     3 5     2 3     5 7     3 2     2 4     4 5     5 6 Después, corríjalas pidiendo a varios alumnos que las lean por orden para que otro compañero las escriba en la pizarra. A continuación, puede trabajar con estas fracciones el reconocimiento de sus términos, su representación, o la comparación de las fracciones que tengan el mismo denominador o el mismo numerador, tanto a nivel colectivo en la pizarra o de forma individual en el cuaderno. 20
15 Resuelve. Marta trabaja en una oficina. Se encarga de comunicarse por teléfono y por correo electrónico con varias empresas. ¿Cuántas llamadas ha hecho Marta a empresas que no son nacionales? ¿Qué fracción de las llamadas han sido? ¿Ha enviado más correos a España o a Europa? ¿Puedes saberlo sin hacer cálculos? ¿Cómo? ¿Cuántos correos ha enviado a Europa? ¿Cuántos ha enviado a América? ¿Cómo lo has averiguado? Problemas 13 Piensa y resuelve. En una fiesta se repartieron 3 tartas en partes iguales entre 10 niños. ¿Qué fracción de tarta le correspondió a cada uno? ¿Fueron más o menos de cuatro décimos? Begoña vende bizcochos partidos en 2 partes iguales. Ha vendido 13 partes. ¿Cuántos bizcochos enteros y partes de bizcocho ha vendido? Exprésalo con un número mixto. 14 Resuelve. Marcos y Concha han partido una barra de pan en 8 partes iguales. Marcos ha comido cinco octavos y Concha ha comido menos que él. ¿Qué fracción de barra ha podido comer Concha? Pedro tiene bombones de varios tipos. Dos octavos son de fresa, un octavo de menta y el resto de avellana. ¿De qué tipo hay más bombones? ¿Y menos? En el colegio hay 250 alumnos. Cuatro quintos de ellos comen en el comedor. ¿Cuántos alumnos comen en el comedor? ¿Cuántos no comen en él? 15 Resuelve. Marta trabaja en una oficina. Se encarga de comunicarse por teléfono y por correo electrónico con varias empresas. ¿Cuántas llamadas ha hecho Marta a empresas que no son nacionales? ¿Qué fracción de las llamadas han sido? ¿Ha enviado más correos a España o a Europa? ¿Puedes saberlo sin hacer cálculos? ¿Cómo? ¿Cuántos correos ha enviado a Europa? ¿Cuántos ha enviado a América? ¿Cómo lo has averiguado? 6 16 Ayer me comí tres cuartos de las peras que tenía. Hoy he comido 2 peras, que eran las que me quedaban. ¿Cuántas peras tenía? Demuestra tu talento 180 llAMADAS 4 5 a empresas nacionales 595 CorrEoS 4 7 a España, 2 7 a Europa y el resto a América 95 ES0000000024590 663006-Unidad 06_22589.indd 95 10/03/2015 13:17:02 UNIDAD 6 12  R. M. 1 1 4 5 5 4 13  •  Le correspondió 3 10 de tarta a cada uno; es decir, menos de cuatro décimos. •  13 2 5 6 1 2 . Ha vendido 6 bizcochos y medio. 14  • Ha podido comer 1 8 , 2 8 o 3 8 . •  Fresa: 2 8 . Menta: 1 8 . Avellana: 5 8 . Hay más de avellana y menos de menta. •  4 5 de 250 5 200 250 2 200 5 50 Comen 200 alumnos y no comen 50. 15  •  4 5 de 180 5 144 180 2 144 5 36 Ha hecho 36 llamadas. •  Han sido 1 5 de las llamadas. •  4 7 . 2 7 . Más a España. •  2 7 de 595 5 170 Ha enviado 170 correos a Europa. •  1 7 de 595 5 85 Ha enviado 85 correos a América. Demuestra tu talento 16  2 peras son 1 4 de las peras, luego el total de las peras es 8. Notas Competencias •  Competencia social y cívica. Al realizar la actividad 15, puede llevar a cabo un debate con los alumnos sobre distintos temas relacionados con la competencia y con el contexto que aparece en ella: el mundo del trabajo y la relación con personas de otras empresas y países. Pida a los alumnos que enuncien conductas o valores positivos que deban tener lugar en ese entorno y cómo pueden influir en una relación cordial y productiva. 21
Comprender noticias con fracciones 1 Lee la noticia y resuelve. ¿Qué fracción de los asistentes a yoga correspondió a adultos? ¿Y de los asistentes a gimnasia? ¿Cuál de las dos fracciones es mayor? ¿Qué fue mayor: la fracción de mayores asistentes a yoga o la fracción de adultos? ¿Cómo lo has averiguado? ¿Cuántos jóvenes asistieron a yoga? ¿Cuántos mayores asistieron a gimnasia? Ordena, de menor a mayor número, los tipos de asistentes a yoga. ¿Cómo lo has hecho? 2 TRABAJO COOPERATIVO. Averigua con tu compañero si estas oraciones son correctas. Si es posible, hacedlo sin calcular. Hubo más mayores en yoga que jóvenes. Hubo más mayores en gimnasia que en yoga. Hubo más jóvenes en yoga que mayores. SABER HACER El pueblo del deporte En la localidad de Villares se celebró ayer la XII Jornada Deportiva municipal. Gente de todas las edades participó, superando la asistencia de otros años. Por ejemplo, mil doscientas personas probaron la actividad de yoga y ochocientas personas se acercaron a la zona de gimnasia. La distribución por edades fue la siguiente: Jóvenes Adultos Mayores Yoga Gimnasia 96 ES0000000024590 663006-Unidad 06_22589.indd 96 10/03/2015 13:17:05 Propósitos •  Desarrollar la competencia matemática resolviendo situaciones de la vida real. •  Repasar contenidos clave. Actividades pág. 96 1   •  Adultos en yoga: 2 6 . Adultos en gimnasia: 2 8 . Es mayor la de adultos en yoga. •  Mayores en yoga: 1 6 . Adultos en yoga: 2 6 . Es mayor la de adultos en yoga. •  3 6 de 1.200 5 600 Asistieron a yoga 600 jóvenes. •  2 8 de 800 5 200 Asistieron a gimnasia   200 mayores. •  Mayores , adultos , jóvenes 2   •  1 6 , 3 6 . Falso. •  2 8 . 1 6 . Verdadero. •  3 6 . 1 6 . Verdadero. Actividades pág. 97 1   •  320.500. Trescientos veinte mil quinientos. •  706.096: Setecientos seis mil noventa y seis. •  2.700.009. Dos millones setecientos mil nueve. •  6.091.000. Seis millones noventa y un mil. 2   •  5.821 •  538 •  10.574 •  4.025 •  12.717 •  36.028 3   •  28.623 •  c 5 958, r 5 8 •  175.820 •  271 •  349.520 •  c 5 378, r 5 17 4   •  8 2 2 5 6 •  7 3 4 5 28 •  3 2 3 5 0 •  10 1 4 5 14 •  9 2 8 5 1 •  6 : 3 5 2 Desarrollo de la competencia matemática •  Los contextos reales de aplicación de lo aprendido en la unidad permiten   un desarrollo potente de esta competencia. El contexto ofrecido, las noticias en medios de comunicación, resulta próximo a los alumnos. Al comprobar las respuestas, preste especial atención a las explicaciones de los alumnos sobre sus procesos de razonamiento. Cuando realicen el trabajo cooperativo, pida a cada grupo que aporte varias afirmaciones correctas más, utilizando los gráficos de la página, y que den también razón de cómo han analizado la corrección de las tres afirmaciones propuestas. Inteligencia interpersonal 22
4 Calcula. 8 2 (5 2 3) (9 2 2) 3 4 8 2 5 2 3 10 1 8 : 2 9 2 2 3 4 (8 2 2) : 3 5 Estima estas operaciones. 675 1 492 2.708 1 1.611 914 2 236 5.333 2 2.638 675 3 2 3.194 3 7 6 Escribe el número que representa cada número romano. VI XIII CIV MCM 7 Completa. 8 3 (2 1 …) 5 8 3 … 1 8 3 4 (7 2 3) 3 … 5 … 3 5 2 … 3 5 1 Escribe el número y cómo se lee. 3 CM 1 2 DM 1 5 C 7 CM 1 6 UM 1 9 D 1 6 U 2 U. de millón 1 7 CM 1 9 U 6 U. de millón + 9 DM 1 1 UM 2 Calcula. 1.039 1 4.782 3.456 2 2.918 9.675 1 899 4.911 2 886 12.099 1 618 37.902 2 1.874 3 Calcula. Después, haz la prueba de las divisiones. 329 3 87 8.630 : 9 745 3 236 6.504 : 24 1.028 3 340 13.247 : 35 8 Los 312 alumnos de un colegio van a viajar en autobuses con capacidad para 52 plazas cada uno. ¿Cuántos autobuses serán necesarios? 9 Marisol tenía 8 billetes de 20 € y 3 billetes menos de 50 €. Quiere comprar una lavadora que cuesta 400 €. ¿Tendrá suficiente dinero? 10 Eugenio le dice a su nieta Elena: ¿Qué es mejor: recibir cada día del año 20 € o cada mes del año 600 €? 11 En el almacén envasaron 1.500 kg de lentejas en sacos de 12 kg. Vendieron 80 sacos. ¿Cuántos kilos de lentejas les quedaron? 12 Mercedes compró 25 sillas a 90 € cada una. Las vendió 18 € más caras, pero le quedaron 4 sillas sin vender. ¿Ganó dinero? ¿Cuánto? 13 Raúl tenía 20 rollos de cuerda de 18 m cada uno. Los ha cortado en trozos de 5 m. ¿Cuántos trozos de 5 m ha obtenido? ¿Y de 3 metros? Problemas REPASO ACUMULATIVO 6 97 ES0000000024590 663006-Unidad 06_22589.indd 97 10/03/2015 13:17:06 UNIDAD 6 5   •  700 1 500 5 1.200 •  900 2 200 5 700 •  700 3 2 5 1.400 •  3.000 1 2.000 5 5.000 •  5.000 2 3.000 5 2.000 •  3.000 3 7 5 21.000 6   •  6      •  13      •  104      •  1.900 7   •  8 3 (2 1 4) 5 8 3 2 1 8 3 4 5 5 48 •  (7 2 3) 3 5 5 7 3 5 2 3 3 5 5 5 20 8   312 : 52 5 6  Serán necesarios 6 autobuses. 9  8 3 20 1 5 3 50 5 410  410 . 400 Sí, tendrá suficiente dinero. 10 365 3 20 5 7.300  12 3 600 5 7.200 Es mejor cada día 20 €. 11  1.500 : 12 5 125 125 2 80 5 45 45 3 12 5 540 Quedaron 540 kg de lentejas. 12 25 3 90 5 2.250  (90 1 18) 3 21 5 2.268 2.268 2 2.250 5 18 Mercedes ganó 18 €. 13  18 : 5   c 5 3, r 5 3 De cada rollo obtiene 3 trozos de 5 m y 1 trozo de 3 m. En total ha obtenido 60 trozos de 5 m y 20 trozos de 3 m. Notas Repaso en común •  Pida a los alumnos que realicen de forma individual las actividades propuestas en esta página. Después, haga una puesta en común con los resultados obtenidos para detectar las dificultades. Puede pedir también a los alumnos que digan en qué actividades han tenido más problemas. Si lo cree conveniente, proponga otras actividades similares a las propuestas para reforzar los contenidos. 23
Números decimales7 Contenidos de la unidad SABER NÚMEROS Y OPERACIONES • Unidades decimales. • Números decimales. • Comparación de decimales. • Aproximación de decimales. SABER HACER NÚMEROS Y OPERACIONES • Reconocimiento de las unidades decimales y sus equivalencias. • Escritura de unidades decimales en forma de fracción y de número decimal. • Lectura y escritura de números decimales. • Diferenciación de la parte entera y decimal de un número decimal. • Descomposición, ordenación y comparación de números decimales. • Aproximación de números decimales a un orden dado. RESOLUCIÓN DE PROBLEMAS • Resolución de problemas ordenando primero los datos. • Ordenación de los datos e invención de una pregunta que se resuelva usando todos ellos.   TAREA FINAL • Estudiar la evolución de un precio. SABER SER FORMACIÓN EN VALORES • Valoración de la utilidad de los decimales para comprender diversas situaciones reales. • Interés por la resolución de problemas. 24
BIBLIOTECA DEL PROFESORADO Programación didáctica de aula Recursos para la evaluación • Evaluación de contenidos. Unidad 7: pruebas de control B y A. • Evaluación por competencias. Prueba 7. •  Rúbrica. Unidad 7. Enseñanza individualizada • Plan de mejora. Unidad 7. • Programa de ampliación. Unidad 7. Proyectos de trabajo cooperativo • Proyecto del segundo trimestre. Recursos complementarios • Fichas para el desarrollo de la inteligencia. • Operaciones y problemas. Aprendizaje eficaz • Técnicas de estudio y presentación de exámenes. Proyectos interdisciplinares • Programa de Educación en valores. • Programa de Educación emocional. • Inteligencias múltiples. RECURSOS DIGITALES LibroMedia • Unidad 7: actividades y recursos. MATERIAL DE AULA Láminas OTROS MATERIALES DEL PROYECTO Cuaderno del alumno • Segundo trimestre. Unidad 7. Solución de problemas. Método DECA SUGERENCIA DE TEMPORALIZACIÓN Enero MarzoFebrero ES0000000024590 663006_Matematicas_4_GRAZ_24259 PRIMARIA PRIMARIA Matemáticas PRIMARIA ANDALUCÍAMatemáticas ANDALUCÍA Matemáticas ANDALUCÍA ES0000 000024 590 663006 _Matem aticas_4_GRA Z_2425 9.indd 1 04/03/2 015 11:21:19 ES0000000024593 663039_Cdno_Matematicas_4-2_22732 PRIMARIA Matemáticas Segundo trimestre Matemáticas Segundo trimestre PRIMARIA CUADERNO CUADERNO ES0000000024593 663039_Cdno_Matematicas_4-2_22732.indd 1 19/02/2015 16:56:18 25
7 Números decimales Cada año más altos Los alumnos de 4.º, desde que iban a Infantil, miden su altura cada año a mitad de curso. Forman grupos de tres y con la cinta métrica se miden unos a otros. En una tabla van anotando las alturas en metros de cada uno. Desde hace tiempo, todos miden 1 metro y muchos centímetros. ¡Algunos quizá lleguen a medir 2 metros de altura! Altura en metros Ana 1 m y 30 cm Carlos 1 m y 26 cm Asun 1 m y 35 cm Ernesto 1 m y 32 cm Julián 1 m y 29 cm 98 ES0000000024590 663006-Unidad 07_22590.indd 98 10/03/2015 13:16:50 Propósitos •  Reconocer situaciones reales en las que se utilicen números decimales. •  Recordar los conceptos básicos necesarios para el desarrollo de la unidad. Previsión de dificultades •  Algunos alumnos pueden tener dificultad en la lectura y escritura   de números decimales cuando   la primera o las dos primeras cifras decimales son cero. Realice actividades de lectura y escritura de números decimales para subsanar estas posibles dificultades. •  Las aproximaciones de decimales plantean en ocasiones dificultades   a los alumnos. Muestre la similitud con el proceso seguido en   los números naturales. Trabajo colectivo sobre la lámina Pida a un alumno que lea la lectura   y pregúnteles si ellos se han medido  alguna vez, si saben cuánto miden, cuál es esa medida, etc.   A continuación, hágales observar la tabla y pregunte a la clase si conocen otra forma de expresar esas estaturas.  Si los alumnos no la aportan, señale que existe otra manera, utilizando los números decimales. Comente que en esta unidad van a trabajar con estos números y que aprenderán muchas cosas sobre ellos. 1 Ana mide 1 m y 30 cm.   Es más alta que Carlos.  Hay 4 cm de diferencia.  La que mide más es Asun y   el que mide menos Carlos. 2 Carlos: 1,26 m.   Asun: 1,35 m.  Ernesto: 1,32 m.   Julián: 1,29 m. 3 R. M. Puede medir 1,27 m   o 1,28 m. También cualquier  otro decimal comprendido entre 1,26 y 1,29. Otras formas de empezar •  Pida a los alumnos que traigan a clase folletos publicitarios, revistas, periódicos…, y que busquen en ellos contextos en los que aparezcan números decimales. Comente con ellos algunos casos. Después, pregúnteles si saben cuál de los números es mayor o menor   y que expliquen por qué. •  Pregunte a los alumnos que si conocen situaciones en las que se utilizan números decimales y pídales que las enumeren. Propóngales que digan por qué creen que son necesarios en esas situaciones los números decimales. 26
¿Qué sabes ya? 1 ¿Cuánto mide Ana? ¿Es más alta que Carlos? ¿Cuántos centímetros hay de diferencia entre ellos? De los cinco alumnos, ¿quién es el que mide más? ¿Y menos? 2 Si escribimos la altura de Ana como 1,30 m, ¿cómo escribirías la altura de los demás alumnos? ¿Cómo se escribiría la altura del más alto? 3 EXPRESIÓN ORAL. ¿Cuánto puede medir Lidia si mide más que Carlos y menos que Julián? Da varias posibilidades. Lee, comprende y razona Fracciones de denominador 10 – Denominador: cada figura está dividida en 10 partes iguales. – Numerador: número de partes coloreadas en cada figura. 2 10 5 10 8 10 dos décimos cinco décimos ocho décimos 1 Escribe cada fracción representada y cómo se lee. 2 Dibuja en tu cuaderno y representa estas fracciones. 3 10 7 10 Un décimo. Seis décimos. 3 Observa las figuras pintadas de cada color y completa en tu cuaderno como en el ejemplo. TAREA FINAL Estudiar la evolución de un precio Al final de la unidad analizarás los cambios de un precio. Antes, trabajarás con los números decimales, los compararás y aproximarás. SABER HACER EJEMPLO … figuras y ... 10 de otra. 99 ES0000000024590 663006-Unidad 07_22590.indd 99 10/03/2015 13:16:51 UNIDAD 7 ¿Qué sabes ya? Repase con los alumnos los conceptos relacionados con las fracciones de denominador 10: lectura, escritura, representación..., ya que están muy relacionados con las décimas, las primeras unidades decimales que estudiarán en la unidad. 1 •  4 10 . Cuatro décimos. •  5 10 . Cinco décimos. •  9 10 . Nueve décimos. 2 R. L. 3 •  2 figuras y 2 10 de otra. •  3 figuras y 6 10 de otra. Notas Competencias •  Comunicación lingüística. Al realizar las actividades propuestas después de la lectura, es importante que los alumnos conozcan y utilicen el lenguaje matemático correctamente para expresarse. •  Aprender a aprender. Exprese a los alumnos la importancia que tiene afianzar y reforzar los conocimientos para poder avanzar sin dificultad. Recuérdeles cómo se representan las unidades decimales, así como su expresión en forma de fracción y en forma decimal. Inteligencia lingüística 27
Unidades decimales 1 Escribe en forma de fracción y en forma de número decimal. 3 décimas 8 centésimas 4 milésimas 5 décimas 5 centésimas 7 milésimas 7 décimas 12 centésimas 92 milésimas 9 décimas 39 centésimas 214 milésimas 2 Copia la tabla en tu cuaderno y complétala. Las unidades decimales se obtienen al dividir la unidad en partes iguales. Se pueden expresar como fracción o como número decimal. Si la unidad se divide en 10 partes iguales, cada parte es 1 décima. 1 unidad 5 10 décimas 1 10 5 0,1 fracción decimal Si la unidad se divide en 100 partes iguales, cada parte es 1 centésima. 1 unidad 5 100 centésimas 1 100 5 0,01 fracción decimal Si la unidad se divide en 1.000 partes iguales, cada parte es una milésima. 1 unidad 5 1.000 milésimas 1 1.000 5 0,001 EJEMPLO 3 décimas 5 3 10 5 0,3 Unidades decimales 18 centésimas 39 milésimas Forma de fracción 7 10 713 1.000 Forma decimal 0,18 0,65 Las equivalencias entre la unidad y las unidades decimales son: 1 unidad 5 10 décimas 5 100 centésimas 5 1.000 milésimas 1 décima 5 10 centésimas 1 centésima 5 10 milésimas 100 ES0000000024590 663006-Unidad 07_22590.indd 100 10/03/2015 13:16:52 Propósitos •  Reconocer las unidades decimales. •  Conocer y aplicar las relaciones entre unidades decimales. Sugerencias didácticas Para explicar. Haga que los alumnos observen el cuadro informativo y explique el significado de décima, centésima y milésima. Escriba en la pizarra cómo se expresan en forma de fracción y en forma decimal. Comente las equivalencias entre las distintas unidades decimales. Para reforzar. Prepare tarjetas de cartulina iguales y escriba en algunas de ellas unidades decimales, en otras sus expresiones como fracción, en otras como decimal y en otras su representación. Coloque las tarjetas con dibujos en fila en el corcho y ponga las demás tarjetas en su mesa, mezcladas y boca abajo. Pida a los alumnos que, por orden, cojan una tarjeta, digan qué unidad es y la coloquen debajo del dibujo correspondiente. Actividades 1   •  3 10 5 0,3 •  5 10 5 0,5 •  7 10 5 0,7 •  9 10 5 0,9 •  8 100 5 0,08 •  5 100 5 0,05 •  12 100 5 0,12 •  39 100 5 0,39 •  4 1.000 5 0,004 •  7 1.000 5 0,007 •  92 1.000 5 0,092 •  214 1.000 5 0,214 2   18 centésimas 5 18 100 5 0,18 7 décimas 5 7 10 5 0,7 65 centésimas 5 65 100 5 0,65 Otras actividades •  Proponga a los alumnos un dictado de unidades decimales. Nombre varias décimas, centésimas o milésimas para que los alumnos escriban en forma de fracción y en forma decimal. Después pida   a un alumno que escriba en la pizarra sus resultados y entre todos   se comprobará si los resultados son o no correctos. Ejemplo: 3 décimas 24 centésimas 934 milésimas 5 décimas 8 centésimas 76 milésimas 28
Problemas 5 Resuelve. Marta ha hecho un mosaico de 100 piezas. – ¿Cuántas centésimas son de color rojo? – ¿Cuántas centésimas son de color amarillo? ¿A cuántas décimas equivalen? – ¿Cuántas centésimas son de color verde? ¿A cuántas décimas y centésimas equivalen? Una parcela ha sido dividida en 1.000 partes iguales y han sembrado 350 de ellas. ¿Cuántas milésimas han sembrado? ¿Cuántas no han sido sembradas? 7 3 Completa en tu cuaderno. Usa las equivalencias. 3 unidades 5 … décimas 7 unidades 5 … décimas 9 unidades 5 … décimas 5 décimas 5 … centésimas 7 décimas 5 … centésimas 8 décimas 5 … centésimas 6 centésimas 5 … milésimas 7 centésimas 5 … milésimas 9 centésimas 5 … milésimas 4 Expresa en la unidad indicada. 2 unidades y 7 décimas 4 unidades y 5 décimas 5 unidades y 2 décimas 6 unidades y 9 décimas 5 unidades y 1 centésima 9 décimas y 8 centésimas 5 unidades y 86 centésimas 4 décimas y 5 centésimas 8 unidades y 4 milésimas 6 centésimas y 25 milésimas 7 unidades y 834 milésimas 2 centésimas y 18 milésimas Problemas 5 Resuelve. Marta ha hecho un mosaico de 100 piezas. – ¿Cuántas centésimas son de color rojo? – ¿Cuántas centésimas son de color amarillo? ¿A cuántas décimas equivalen? – ¿Cuántas centésimas son de color verde? ¿A cuántas décimas y centésimas equivalen? Una parcela ha sido dividida en 1.000 partes iguales y han sembrado 350 de ellas. ¿Cuántas milésimas han sembrado? ¿Cuántas no han sido sembradas? Halla la mitad de decenas y de centenas CÁLCULO MENTAL EJEMPLO 2 unidades y 7 décimas 5 20 décimas 1 7 décimas 5 27 décimas 10 : 2 60 : 2 20 : 2 70 : 2 40 : 2 80 : 2 50 : 2 90 : 2 30 : 2 5 15 100 : 2 600 : 2 200 : 2 700 : 2 300 : 2 800 : 2 400 : 2 900 : 2 500 : 2 5 250 En décimas En centésimas En milésimas 101 ES0000000024590 663006-Unidad 07_22590.indd 101 10/03/2015 13:16:55 UNIDAD 7 39 milésimas 5 39 1.000 5 0,039 713 milésimas 5 713 1.000 5 0,713 3   3 unidades 5 30 décimas 7 unidades 5 70 décimas 9 unidades 5 90 décimas 5 décimas 5 50 centésimas 7 décimas 5 70 centésimas 8 décimas 5 80 centésimas 6 centésimas 5 60 milésimas 7 centésimas 5 70 milésimas 9 centésimas 5 90 milésimas 4   •  27 décimas • 45 décimas •  52 décimas • 69 décimas •  501 centésimas •  586 centésimas •  98 centésimas •  45 centésimas •  8.004 milésimas •  7.834 milésimas •  85 milésimas •  38 milésimas 5   •  Rojo: 8 centésimas. Amarillo: 10 centésimas 5 5 1 décima. Verde: 37 centésimas 5 5 3 décimas y 7 centésimas. • Han sembrado 350 milésimas. 1.000 2 850 5 150 No han sembrado 150 milésimas. Cálculo mental • 5 • 30 • 50 • 300 • 10 • 35 • 100 • 350 • 20 • 40 • 150 • 400 • 25 • 45 • 200 • 450 Notas Competencias • Conciencia y expresión cultural. La realización de dibujos similares al de la actividad 5 permite, por un lado, potenciar la competencia artística y creativa de los alumnos a la vez que, a partir de los dibujos producidos, trabajan los contenidos de esta doble página. Pídales a los alumnos que en una cuadrícula 10 3 10 realicen un dibujo artístico con colores y después trabaje con ellos qué parte es de color, cómo se lee ese número decimal, a qué otras unidades decimales equivale… 29
Números decimales 1 Escribe en tu cuaderno cada número decimal representado. Después, indica cuál es su parte entera y su parte decimal. 2 Escribe un número decimal. Cuya parte entera sea 5. Cuya parte decimal sea 8 décimas. Cuya parte decimal sea 15 centésimas. Cuya parte decimal sea 392 milésimas. Laura está participando en un campeonato de gimnasia. En una de las pruebas ha obtenido 38,752 puntos. El número 38,752 es un número decimal. Un número decimal tiene dos partes, separadas por una coma: Lectura. Los números decimales se pueden leer de dos formas. 38,752 38 coma 752 38 unidades y 752 milésimas Descomposición. 38,752 5 3 decenas 1 8 unidades 1 7 décimas 1 5 centésimas 1 2 milésimas 38,752 5 30 1 8 1 0,7 1 0,05 1 0,002 Los números decimales tienen dos partes: – La parte entera (unidades, decenas, centenas…) a la izquierda de la coma. – La parte decimal (décimas, centésimas, milésimas…) a la derecha de la coma. Parte entera Parte decimal Decenas D Unidades U décimas d centésimas c milésimas m 3 8 , 7 5 2 EJEMPLO 1,7 Parte entera: … Parte decimal: … 102 ES0000000024590 663006-Unidad 07_22590.indd 102 10/03/2015 13:16:57 Propósitos •  Descomponer, leer y escribir números decimales. •  Usar los números decimales   en situaciones reales. Sugerencias didácticas Para explicar. Haga que un alumno lea la situación planteada y escriba en la pizarra el número decimal correspondiente. Comente cuál es su parte entera y decimal, cómo se descompone en sus órdenes y en forma de suma, cuáles son las dos formas de leerlo… Escriba en la pizarra otros casos similares y realice en común estos procedimientos. Muestre la similitud con los procedimientos seguidos con los números naturales y llame la atención sobre la importancia del valor posicional de las cifras. Trabaje en especial algunos casos   de números con ceros intermedios, que tienen mayor dificultad. Actividades 1 •  1,7 Parte entera: 1.  Parte decimal: 7. •  1,013 Parte entera: 1.  Parte decimal: 013. •  3,036 Parte entera: 3.  Parte decimal: 036. 2 R. M. •  5,9 •  4,8 •  3,15 •  1,392 3 •  R. M. 2 unidades y 7 décimas  2 coma 7 •  19 unidades y 36 centésimas •  8 unidades y 123 milésimas •  7 unidades y 68 centésimas •  25 unidades y 3 décimas •  6 unidades y 3 milésimas •  690 unidades y 42 centésimas •  9 unidades y 17 milésimas •  48 unidades y 902 milésimas •  16 unidades y 2 centésimas 4 •  5,4 •  17,9 •  21,37 •  236,08 •  71,008 •  56,042 Otras actividades •  Pida a los alumnos que, durante una semana, busquen y copien varios números decimales que vean en lugares fuera de la clase.   Después, trabaje esos números en común, anotando en qué lugar   los han encontrado, cuál es su escritura, su descomposición,   el valor posicional de sus cifras... 30
7 Piensa y contesta. ¿Entre qué números naturales está comprendido 3,76? ¿Existen números decimales comprendidos entre 8,4 y 8,5? Pon dos ejemplos si crees que sí. ¿Existen números decimales entre 9,27 y 9,28? Pon dos ejemplos si crees que sí. RAZONAMIENTO 3 Escribe de dos formas cómo se lee cada número. 2,7 8,123 25,3 690,42 48,902 19,36 7,68 6,003 9,017 16,02 4 Escribe con cifras cada número decimal. 5 coma 4 17 unidades y 9 décimas 21 coma 37 236 unidades y 8 centésimas 71 coma 008 56 unidades y 42 milésimas 5 Escribe el valor de la cifra 5 en cada número. 28,15 26,015 52,301 7 coma 05 25 coma 937 8 coma 105 6 Descompón cada número. 8,3 4,825 12,609 79,8 9,76 7,34 25,06 210,094 Problemas 7 Resuelve. Expresa el resultado con un número decimal. Marcos tardó 13 segundos y 15 centésimas en correr 100 metros. Leonor tardó 26 centésimas más. ¿Cuánto tardó Leonor? Marisa tenía 25 euros y 70 céntimos. Compró un pantalón por 13 euros y 25 céntimos. ¿Cuánto dinero le quedó? EJEMPLO 28,15 5 centésimas 5 0,05 103 ES0000000024590 663006-Unidad 07_22590.indd 103 10/03/2015 13:16:58 UNIDAD 7 5 • 5 centésimas 5 0,05 • 5 milésimas 5 0,005 • 5 decenas 5 50 unidades • 5 centésimas 5 0,05 • 5 unidades 5 5 • 5 milésimas 5 0,005 6 • 8 U 1 3 d 5 8 1 0,3 • 9 U 1 7 d 1 6 c 5 5 9 1 0,7 1 0,06 • 4 U 1 8 d 1 2 c 1 5 m 5 5 4 1 0,8 1 0,02 1 0,005 • 7 U 1 3 d 1 4 c 5 5 7 1 0,3 1 0,04 • 1 D 1 2 U 1 6 d 1 9 m 5 5 10 1 2 1 0,6 1 0,009 • 2 D 1 5 U 1 6 c 5 5 20 1 5 1 0,06 • 7 D 1 9 U 1 8 d 5 5 70 1 9 1 0,8 • 2 C 1 1 D 1 9 c 1 4 m 5 5 200 1 10 1 0,09 1 0,004 7 • Marcos: 13,15 s. 15 1 26 5 41 Leonor: 13,41 s. Leonor tardó 13,41 segundos. • Marisa: 25,70 €. 25 2 13 5 12 70 2 25 5 45 Le quedaron 12,45 €. Razonamiento • Entre 3 y 4. • Sí, existen infinitos números decimales. Por ejemplo: 8,41, 8,412... • Sí, existen infinitos números decimales. Por ejemplo: 8,271, 8,272... Notas Otras actividades • Realice actividades de paso de unas expresiones a otras para potenciar la comprensión de los números decimales. Enuncie o escriba una de las expresiones posibles (con cifras, con letras de una de las dos formas, descompuesta en forma de suma, descompuesta en sus órdenes…) y pida a los alumnos que determinen todas las otras. • Escriba varias expresiones de números decimales en la pizarra. Los alumnos deberán determinar cuáles de ellas corresponden a un mismo número decimal. Aproveche para trabajar los números con ceros ya que suelen plantear especiales dificultades. 31
Comparación de números decimales 1 Copia los números en tu cuaderno y rodea. 6,75 y 9,13 9,036 y 9,032 27,34 y 27,61 18,35 y 18,62 8,4 y 8,399 6,45 y 7,1 28,16 y 28,09 39,106 y 39,2 2 Ordena cada grupo de números como se indica. Usa el signo correspondiente. El modelo Veloz ha tardado 19,638 segundos en recorrer el circuito, mientras que el modelo Rayo ha tardado 19,64 segundos. ¿Cuál ha tardado menos? Compara 19,638 y 19,64 1.º Compara las partes enteras. 19,638 19,64 2.º Como las partes enteras son iguales, compara las décimas. 19,638 19,64 3.º Como las décimas son iguales, compara las centésimas. 19,638 19,64 Luego 19,638 , 19,64. Ha tardado menos el modelo Veloz. Al comparar números decimales, primero se comparan las partes enteras. Si son iguales, se comparan las décimas, centésimas, milésimas… 19 5 19 6 5 6 3 , 4 El número mayor El número menor 3 Escribe tres números mayores que 4 cuya parte decimal sea menor que 75. De menor a mayor De mayor a menor 3,6 3,59 3,475 7,9 7,84 7,82 2,83 2,834 2,9 2,87 8,15 8,2 8,179 9,5 9,52 9,253 12,34 12,39 12,4 12,397 104 ES0000000024590 663006-Unidad 07_22590.indd 104 10/03/2015 13:16:59 Propósitos •  Comparar números decimales. •  Ordenar series de números decimales de menor a mayor   o viceversa. Sugerencias didácticas Para explicar. Lea la situación planteada y escriba en la pizarra los dos números decimales. Pregunte   a los alumnos qué procedimiento seguían para comparar dos números naturales. Una vez recordado, explique el procedimiento que hay que seguir para comparar dos números decimales. Indique las similitudes entre ambos, comentando que para comparar decimales hay que comparar primero sus partes enteras, que son números naturales. Deje claro que un número decimal con menos cifras que otro no tiene por qué ser menor que él (error común). Actividades 1 •  9,13 •  9,036 •  27,61 •  18,62 •  8,399 •  6,45 •  28,09 •  39,106 2 •  3,475 , 3,59 , 3,6 •  7,82 , 7,84 , 7,9 •  2,83 , 2,834 , 2,87 , 2,9 •  8,2 . 8,179 . 8,15 •  9,52 . 9,5 . 9,253 •  12,4 . 12,397 . 12,39 . 12,34 Notas Otras actividades •  Pida a los alumnos que escriban un número decimal en un folio que cumpla una cierta condición dada por usted (por ejemplo: su parte entera es 12;   está comprendido entre 3 y 4; tiene dos cifras decimales…). Después, saque a varios a la pizarra y pídales que viendo sus números se ordenen de menor a mayor o de mayor a menor. Cuando lo hayan hecho, la clase determinará   si su ordenación es correcta o no.  Una vez establecido el orden, pida a un alumno que diga un número decimal comprendido entre dos de los números, entre qué naturales está uno   de los decimales, un número decimal mayor que el más grande de   los escritos que tenga su misma parte entera o decimal… 32
7Aproximación de números decimales Fíjate en cómo se aproximan estos números decimales. ¿Cómo se aproxima 3,7 a las unidades? 1.º Busca entre qué unidades está. Está entre 3 y 4. 2.º Elige la unidad más próxima. Para ello compara la cifra de las décimas con 5. 7 . 5 La aproximación a las unidades es 4. ¿Cómo se aproxima 9,481 a las centésimas? 1.º Busca entre qué centésimas está. Está entre 9,48 y 9,49. 2.º Elige la centésima más próxima. Para ello compara la cifra de las milésimas con 5. 1 , 5 La aproximación a las centésimas es 9,48. 3,7 4 7 . 5 3 1 1 5 4 9,481 9,48 1 , 5 8 5 8 3 3,43,2 3,6 3,93,1 3,5 3,83,3 3,7 4 9,48 9,481 9,4859,483 9,487 9,4899,482 9,4869,484 9,488 9,49 1 Aproxima cada número decimal al orden indicado. 6,4 7,2 8,8 9,3 11,6 21,7 8,72 5,49 7,18 10,11 25,63 42,91 0,726 8,124 9,017 4,777 4,771 19,818 2 Escribe dos números decimales cuya aproximación a las décimas sea 8,4. A las unidades A las décimas A las centésimas Halla la mitad de números de 2 y de 3 cifras (todas pares) CÁLCULO MENTAL 48 : 2 68 : 2 24 : 2 84 : 2 26 : 2 88 : 2 64 : 2 5 32 486 : 2 5 243 242 : 2 688 : 2 426 : 2 846 : 2 468 : 2 864 : 2 105 ES0000000024590 663006-Unidad 07_22590.indd 105 10/03/2015 13:17:00 UNIDAD 7 Propósitos •  Aproximar números decimales a las unidades, décimas y centésimas. Sugerencias didácticas Para empezar. Realice actividades de aproximación de números naturales. Para explicar. Muestre la similitud con el trabajo realizado al aproximar los números naturales. Deje claro que el número decimal obtenido en cada caso será un número natural,   un número con una cifra decimal   o un número con dos cifras decimales. En este curso hemos aproximado cada número al orden inmediatamente menor que él. Puede extender el trabajo a aproximaciones a órdenes menores (un número   de tres cifras decimales a las décimas o unidades) si lo cree conveniente. Actividades 1 •  6 7 9 9 12 22 •  8,7 5,5 7,2 10,1 25,6 42,9 •  0,73 8,12 9,02     4,78 4,77 19,82 2 R. M. 8,43        8,42        8,39        8,37 Cálculo mental • 24 • 34 • 121 • 344 • 12 • 42 • 213 • 423 • 13 • 44 • 234 • 432 Notas Otras actividades • Utilizando las tarjetas con números decimales realizadas en el apartado Otras actividades de la página anterior, pida a distintos alumnos   que salgan a la pizarra y trabajen las aproximaciones. Por ejemplo, pida  a cada uno de ellos que aproxime al orden inmediatamente menor   su número. La clase comprobará si su respuesta es correcta o no.  Después, pida a todos que digan dos números cuya aproximación  a ese orden sea la misma que la de ese número. Inteligencia espacial 33
Escribe cada problema colocando los datos en el lugar adecuado. Después, resuelve. 1 A la peluquería fueron el viernes 28 personas. De ellas, 10 eran mujeres, 45 hombres (algunos menos que mujeres) y el resto niños. ¿Cuántos niños fueron a la peluquería? 2 Juan pesa 5 kg, su hermano Raúl 20 kg menos que él, y su hermana Rosa, la más pequeña, pesa 48 kg menos que Raúl. ¿Cuántos kilos pesan los tres juntos? 3 Marta tenía 370 billetes de 18 € y 20 € en monedas. Ha comprado una cámara fotográfica de 15 €. ¿Cuánto dinero le ha sobrado? 4 En el almacén han envasado 5 kg de patatas. La mitad la han puesto en bolsas de 400 kg y el resto, en bolsas el doble de grandes, de 70 kg cada una. ¿Han obtenido más de 10 bolsas? Lee el problema y escríbelo de nuevo poniendo los datos en su lugar correspondiente. Después, revísalo y resuélvelo en tu cuaderno. En la fábrica trabajan 400 días de los 340 días de cada año. Cada día envasan 13 botes, que venden a 365 € cada uno. ¿Cuánto dinero obtienen al año por la venta? Al leer el problema vemos que hay datos mal colocados. Un año no tiene 340 días ni se pueden trabajar 400 días en un año. El problema con los datos bien colocados queda así: En la fábrica trabajan 340 días de los 365 días de cada año. Cada día envasan 400 botes, que venden a 13 € cada uno. ¿Cuánto dinero obtienen al año por la venta? Resuelve el problema en tu cuaderno. Ordenar los datos de un problema Solución de problemas 106 ES0000000024590 663006-Unidad 07_22590.indd 106 10/03/2015 13:17:01 Propósitos •  Ordenar los datos de un problema   y resolverlo. •  Ordenar los datos de un problema   e inventar una pregunta. Sugerencias didácticas Para explicar. Haga que los alumnos lean el problema y explíqueles que   los datos de este problema están desordenados y que debemos colocarlos en su lugar correspondiente. Deles un tiempo para pensar y, después, vaya razonando en común en qué lugar debe quedar cada dato. Muestre la importancia de analizar, una vez cambiados de lugar los datos, si el problema tiene sentido. Actividades 1   A la peluquería fueron el viernes 45 personas. De ellas 28 eran mujeres, 10 hombres (algunos menos que mujeres) y el resto niños. ¿Cuántos niños fueron a la peluquería?   45 2 28 2 10 5 45 2 38 5 7  A la peluquería fueron 7 niños. 2   Juan pesa 48 kg, su hermano Raúl 5 kg menos que él, y su hermana Rosa, la más pequeña, pesa 20 kg menos que Raúl. ¿Cuántos kilos pesan los tres juntos? 48 1 43 1 23 5 114  Los tres juntos pesan 114 kg. 3   Marta tenía 18 billetes de 20 €   y 15 € en monedas. Ha comprado una cámara fotográfica de 370 €. ¿Cuánto dinero le ha sobrado? 18 3 20 1 15 5 375  375 2 370 5 5  Le han sobrado 5 €. 4   En un almacén han envasado   400 kg de patatas. La mitad la han puesto en bolsas de 5 kg y el resto en bolsas el doble de grandes, de 10 kg cada una. ¿Han obtenido más de 70 bolsas?  (400 : 2) : 5 5 40; 200 : 10 5 20 40 1 20 5 60  No, han obtenido 60 bolsas. Otras actividades •  Forme grupos de 4 alumnos y pida a dos de ellos que inventen y escriban   un problema. Después, en otra hoja, lo reescribirán con los datos desordenados y se lo plantearán a los otros componentes del grupo   para que coloquen los datos en el lugar correspondiente y lo resuelvan.   Más tarde, cada grupo comprobará el desempeño del otro. A continuación, haga una puesta en común con las propuestas dadas   por los distintos grupos y resuelva algunos de los problemas propuestos   de forma colectiva. 34
Coloca los datos en el lugar adecuado e inventa una pregunta que se resuelva usando todos ellos. Después, resuélvela. 7 Coloca los datos en el lugar correcto e inventa los datos que faltan. Después, resuelve cada problema. 5 Marcos tiene que llevar en su furgoneta cuatro paquetes. El rojo es el más ligero, pesa 98 kg, el verde pesa más que él, y más aún pesan el azul y el morado, que pesan 85 kg. ¿Cuántos kilos pesan todos juntos? 6 Mónica ha comprado 3 kg de peras a 16 € el kilo y el doble de kg de manzanas, a 4 € el kg. El kilo de manzanas es más barato que el de peras. ¿Cuánto le han costado las manzanas más que las peras? 7 Jaime tenía varias monedas de 28 € y 20 billetes de 2 €. Compró un pantalón por 3 €, y un libro más barato que el pantalón. ¿Cuánto dinero le sobró? 8 La familia Sánchez ha ido al teatro. Han ido 12 adultos, 4 de ellos jubilados, y el triple de niños que de adultos, 5. La entrada de jubilado cuesta 3 €, la de niño cuesta un poco más y la de adulto es la más cara. ¿Cuánto han pagado por todas las entradas? INVENTA TUS PROBLEMAS Coloca los datos en el lugar adecuado e inventa una pregunta que se resuelva usando todos ellos. Después, resuélvela. Silvia mide 80 cm y su hermano pequeño mide 145 cm menos que ella. Micaela entrenó durante tres días. El primero entrenó menos, 45 minutos; el segundo algo más, 29 minutos, y el tercero aún más, 32 minutos. César preparó 35 bandejas de pasteles. En cada una había 3 pasteles de fresa y algunos más de chocolate. En total en cada bandeja había 15 pasteles. 1 2 3 107 ES0000000024590 663006-Unidad 07_22590.indd 107 10/03/2015 13:17:02 UNIDAD 7 5   R. M. Marcos tiene que llevar en su furgoneta cuatro paquetes. El rojo es el más ligero, pesa 85 kg, el verde pesa 88 kg y el azul y el morado pesan 98 kg. ¿Cuántos kilos pesan juntos? 85 1 88 1 2 3 98 5 369 Pesan 369 kg. 6   R. M. Mónica ha comprado 16 kg de peras a 4 € el kilo y el doble de kilos de manzanas, a 3 € el kilo. ¿Cuánto le han costado las manzanas más que las peras? 16 3 4 5 64; 16 3 2 3 3 5 96 96 2 64 5 32 Han costado 32 € más. 7   R. M. Jaime tenía 4 monedas de 2 € y 3 billetes de 20 €. Compró un pantalón por 28 € y un libro por 19 €. ¿Cuánto dinero le sobró? 4 3 2 1 3 3 20 5 68 68 2 (28 1 19) 5 21 Le sobraron 21 €. 8   R. M. La familia Sánchez ha ido al teatro. Han ido 4 adultos, 3 de ellos jubilados, y el triple de niños que de adultos, 12. La entrada de jubilado cuesta 5 €, la de niño 6 € y la de adulto 10 €. ¿Cuánto han pagado por las entradas? 1 3 10 1 3 3 5 1 12 3 6 5 97 Han pagado 97 €. Inventa tus problemas 1   R. M. Silvia mide 145 cm y su hermano pequeño mide 80 cm menos que ella. ¿Cuántos centímetros mide Silvia más que su hermano? Mide 65 cm más. 2   R. M. Micaela entrenó durante tres días. El primer día entrenó menos, 29 minutos, el segundo día más, 32 minutos y el tercer día aún más, 45 minutos. ¿Cuánto tiempo entrenó? Entrenó 106 minutos. 3   R. M. César preparó 3 bandejas de pasteles. En cada bandeja había 15 pasteles de fresa y algunos más de chocolate. En cada bandeja había 35 pasteles. ¿Cuántos pasteles de chocolate había? Había 60 pasteles de chocolate. Competencias •  Iniciativa y emprendimiento. Las actividades de invención de problemas son un contexto que permite a los alumnos profundizar en el desarrollo de esta competencia. Pida a los alumnos que a la hora de inventar preguntas sean lo más creativos posible y que no olviden comprobar la corrección del problema planteado. 35
6 Escribe de dos formas cómo se lee cada número. 1,4 9,37 15,304 0,8 8,06 31,008 7 Escribe con cifras. 2 unidades y 9 centésimas 3 unidades y 28 milésimas 15 unidades y 7 décimas 20 unidades y 106 milésimas 8 Descompón cada número decimal. 3,9 6,504 28,003 2,17 12,03 145,207 9 ¿Qué número es? Escribe. 2 unidades 1 4 décimas 3 unidades 1 2 centésimas 8 décimas 1 6 milésimas 3 unidades 1 2 décimas 1 1 milésima 10 VOCABULARIO. Explica cómo se comparan dos números decimales. Ayúdate con un ejemplo. 11 Compara. 3,5 y 3,49 2,704 y 2,706 8,004 y 8,1 9,4 y 9,402 6,72 y 6,719 4,999 y 4,996 12 Aproxima cada número al orden indicado. A las unidades: 9,4 6,8 6,9 7,1 A las décimas: 6,73 2,91 8,39 4,06 A las centésimas: 3,676 2,119 8,462 1 Expresa la parte coloreada como fracción y como número decimal. 2 Expresa como número decimal. 4 décimas 28 centésimas 275 milésimas 3 milésimas 3 10 29 100 37 1.000 5 100 145 1.000 7 1.000 3 Utiliza las equivalencias y expresa en la unidad indicada. En décimas 4 unidades 6 unidades 2 unidades y 4 décimas En centésimas 3 unidades 5 unidades 4 unidades y 25 centésimas En milésimas 7 unidades 8 unidades 5 unidades y 125 milésimas 4 Copia en tu cuaderno y rodea de rojo la parte entera y de verde, la decimal. 1,4 9,057 65,102 37,82 8,31 316,04 5 Expresa cada precio como un número decimal. 5 € y 21 céntimos 6 céntimos 4 € y 2 céntimos 14 céntimos 28 € y 50 céntimos 70 céntimos ACTIVIDADES 108 ES0000000024590 663006-Unidad 07_22590.indd 108 10/03/2015 13:17:03 Propósitos •  Repasar los contenidos básicos   de la unidad. Actividades 1   •  7 10           •  6 100           •  57 100 2   •  0,4 •  0,28 •  0,275 •  0,003 •  0,3 •  0,29 •  0,037 •  0,05 •  0,145 •  0,007 3   •  40 décimas           •  60 décimas •  24 décimas •  300 centésimas •  500 centésimas •  425 centésimas •  7.000 milésimas •  8.000 milésimas •  5.125 milésimas 4   •  1 •  9 •  65 4 057 102 •  37 •  8 •  316 82 31 04 5   •  5,21 € •  0,06 € •  4,02 € •  0,14 € •  28,50 € •  0,70 € 6   •  R. M. 1 unidad y 4 décimas  1 coma 4 •  8 décimas •  9 unidades y 37 centésimas •  8 unidades y 6 centésimas •  15 unidades y 304 milésimas •  31 unidades y 8 milésimas 7   •  2,09 •  15,7 •  3,028 •  20,106 8   •  3 U 1 9 d 5 3 1 0,9 •  2 U 1 1 d 1 7 c 5   5 2 1 0,1 1 0,07 •  6 U 1 5 d 1 4 m 5   5 6 1 0,5 1 0,004 •  1 D 1 2 U 1 3 c 5  5 10 1 2 1 0,03 •  2 D 1 8 U 1 3 m 5  5 20 1 8 1 0,003 •  1 C 1 4 D 1 5 U 1 2 d 1 7 m 5 5 100 1 40 1 5 1 0,2 1 0,007 Otras actividades •  Escriba en la pizarra varios números decimales escritos de distintas formas. Por ejemplo: 5,087              3 unidades y 9 centésimas 3 unidades 1 5 décimas 1 8 milésimas            3 1 0,7 1 0,002 Pídales que se fijen en un número y haga que escriban su expresión   con cifras o letras, su descomposición o su lectura. También puede pedirles que los ordenen de menor a mayor. 36
BA C Problemas 13 Resuelve. El modelo A ha gastado 6,9 litros en recorrer 100 km, el modelo B 6,85 litros y el C ha gastado más que el B pero menos que el A. ¿Cuánto ha podido gastar el modelo C? Carlos tenía 2 monedas de 2 €, 1 moneda de 10 céntimos y 3 monedas de 2 céntimos. ¿Puede comprar un cuaderno que cuesta 4,15 €? 14 Resuelve. Lara ha tardado en nadar una distancia 2 minutos y 9 décimas; José, 2 minutos y 9 milésimas, y Olga, 2 minutos y 9 centésimas. ¿Quién ha llegado el primero a la meta? David ha saltado 6,7 m de longitud y Lidia 5,2 m. ¿Cuántos metros ha saltado aproximadamente cada uno? Miguel ha comprado un pantalón por 35,62 €, una camisa por 17,26 € y un abrigo por 80,19 €. ¿Cuánto cuesta aproximadamente cada prenda? 15 Observa la tabla y resuelve. Observa las temperaturas máximas y mínimas en grados centígrados de varias localidades en un año. ¿Qué lugar tuvo la temperatura máxima más alta? ¿Y la mínima más baja? Luisa quiere ir a veranear a un lugar que tuviera menos de 36 ºC de máxima. ¿A cuáles podrá ir? Pedro quiere ir en invierno a un lugar que tuviera más de 1 ºC de mínima. ¿A cuáles podrá ir? 7 16 Ordena de menor a mayor estos números. ¿Cómo lo haces? 0,7 71 100 0,69 695 1.000 Demuestra tu talento Lugar Villares Valverde Cerrillo Cobijo Máxima 32,5 34,9 37,8 33,8 Mínima 1,6 0,5 1,2 0,9 109 ES0000000024590 663006-Unidad 07_22590.indd 109 10/03/2015 13:17:04 UNIDAD 7 9   •  2,4 •  0,806 •  3,02 •  3,201 10  R. L. 11  •  3,5 . 3,49 •  2,704 , 2,706 •  8,004 , 8,1 •  9,4 , 9,402 •  6,72 . 6,719 •  4,999 . 4,996 12  •  9  7  7  7 •  6,7 2,9 8,4 4,1 •  3,68  2,12  8,46 13  •  Ha podido gastar 6,86 ℓ; 6,87 ℓ; 6,88 ℓ o 6,89 ℓ. •  2 3 2 1 0,10 1 3 3 0,02 5 5 4,16 € Sí, puede comprarlo. 14  •  Lara: 2,9 min José: 2,009 min Olga: 2,09 min Ha llegado primero José. •  David: 7 m aprox. Lidia: 2 m aprox. •  Pantalón: 35,60 €. Camisa: 17,30 €. Abrigo: 80,20 €. 15  •  Cerrillo: 37,8 ºC. Valverde: 0,5 ºC. •  Villares, Valverde y Cobijo. •  Villares y Cerrillo. Demuestra tu talento 16   Escribimos las fracciones en forma de número decimal y, después, comparamos. 0,7        0,71        0,69        0,695 0,69 , 695 1.000 , 0,7 , 71 100 Notas Competencias •  Competencia matemática, científica y tecnológica. La situación presentada en la actividad 15 presenta un contexto en el que se relacionan las Matemáticas con conceptos del ámbito científico como son las temperaturas máximas y mínimas. Señale la relación existente entre las diferentes disciplinas de este ámbito y anímelos a buscar y utilizar, siempre que puedan, esas conexiones. Pídales que planteen a sus compañeros preguntas similares a las ofrecidas. 37
Estudiar la evolución de un precio En la clase de 4.º están haciendo un trabajo sobre la variación en los precios de los combustibles. Han representado en un gráfico el precio medio en euros de un litro en algunos meses de 2014. SABER HACER 1 Observa el gráfico y resuelve. ¿Cuánto valía el litro de gasoil en marzo? ¿Y el de gasolina en mayo? ¿En qué mes aumentó el precio del gasoil con respecto al mes anterior? ¿En qué meses fue igual el precio de la gasolina? ¿En qué meses el litro de gasoil costaba más de 1,35 €? ¿En qué meses el litro de gasolina costaba menos de 1,41 €? 2 TRABAJO COOPERATIVO. Resuelve con tu compañero. Redondead cada precio del gráfico a los céntimos de euro y contestad de nuevo las preguntas de la actividad 1. ¿Hay alguna diferencia con las respuestas obtenidas anteriormente? 1,42 1,41 1,4 1,39 1,38 1,37 1,36 1,35 1,34 1,33 1,32 1,31 1,3 Enero JunioMayoAbrilMarzoFebrero Gasoil Gasolina 1,404 1,411 1,401 1,412 1,355 1,355 1,338 1,346 1,3381,338 1,402 1,402 110 ES0000000024590 663006-Unidad 07_22590.indd 110 10/03/2015 13:17:06 Inteligencia interpersonal Propósitos •  Desarrollar la competencia matemática resolviendo   una situación real. •  Repasar contenidos básicos. Actividades pág. 110 1   •  Gasoil en marzo: 1,338 €. Gasolina en mayo: 1,402 €. •  Aumentó en junio. •  En abril y mayo. •  En enero y febrero. •  En enero, marzo, abril y mayo. 2   Gasolina: 1,40 1,41 1,40  1,40 1,40 1,41  Gasoil: 1,36 1,36 1,34  1,34 1,34 1,35 •  Gasoil en marzo: 1,34 €. Gasolina en mayo: 1,40 €. •  Aumentó en junio. •  En enero, marzo, abril y mayo. •  En enero y febrero. •  En enero, marzo, abril y mayo. Actividades pág. 111 1   •  200.071 •  8.402.093 •  3 4 •  1 5 •  7 10 •  2 6 2   •  96.108 •  c 5 3.619, r 5 5 •  87.788 •  c 5 762, r 5 14 •  344.454 •  c 5 1.236, r 5 40 3   •  7 2 6 5 1 •  3 1 10 2 1 5 12 •  9 2 5 5 4 •  8 : 8 1 3 5 4 •  3 2 1 5 2 •  9 2 2 2 6 5 1 4   •  Siete novenos. •  Tres octavos. •  Nueve décimos. •  Cuatro quintos. 5   •  11 5 y 10 7 6   •  2 3 . 2 5 •  8 10 . 3 10 •  5 2 . 5 7   Desarrollo de la competencia matemática •  En esta página los alumnos tienen que aplicar distintos conceptos estudiados en la unidad para resolver una situación de la vida real. Hágales observar en el gráfico que el precio de los combustibles   varía de un mes a otro. A la hora de abordar el trabajo cooperativo,   pídales que intenten expresar los nuevos datos de forma gráfica. También puede ser interesante que busquen información actualizada sobre los precios de ambos combustibles en fechas próximas. 38
4 Escribe cómo se lee cada fracción. 7 9 3 8 9 10 4 5 5 Copia en tu cuaderno las fracciones que sean impropias. 11 5 7 10 10 7 6 9 6 Compara cada pareja de fracciones. 7 Calcula. 2 3 de 120 4 5 de 165 Seis octavos de 160. 1 Escribe con cifras. Doscientos mil setenta y uno Ocho millones cuatrocientos dos mil noventa y tres Tres cuartos Un quinto Siete décimos Dos sextos 2 Calcula. 86.234 1 9.874 28.957 : 8 91.663 2 3.875 31.256 : 41 921 3 374 68.020 : 55 3 Calcula. 7 2 2 3 3 3 1 2 3 5 2 1 9 2 (6 2 1) 8 : (2 1 6) 1 3 9 2 6 2 1 9 2 8 : 4 2 6 8 María ha cocinado 200 pasteles. Tres quintos son de chocolate y el resto de fresa. ¿De qué sabor ha cocinado más pasteles? 9 A una excursión se apuntaron 25 personas, que pagaban 20 € cada una. Se borraron 5 personas. ¿Cuánto tuvo que pagar cada una de las que quedaron si el precio total seguía siendo el mismo? 10 Sonia ha pintado tres séptimos de una figura y Laura ha pintado tres cuartos de una figura igual. ¿Cuál ha pintado más? 11 Se han envasado 15.000 bolígrafos en cajas de 6 unidades. Después, se hicieron paquetes de 8 cajas. ¿Cuántos paquetes se han obtenido? ¿Sobraron cajas? 12 En Valverde cosecharon 25.000 kg de patatas. Se quedaron 1.800 kg y el resto lo envasaron en sacos de 50 kg. ¿Cuántos sacos obtuvieron? 13 Un quinto de los 180 alumnos de Dibujo vienen a clase en bicicleta. La mitad de ellos son chicas. ¿Cuántas chicas vienen a clase en bicicleta? Problemas REPASO ACUMULATIVO 7 2 3 y 2 5 8 10 y 3 10 5 2 y 5 7 111 ES0000000024590 663006-Unidad 07_22590.indd 111 10/03/2015 13:17:06 UNIDAD 7 7 •  2 3 de 120 5 80 •  4 5 de 165 5 132 •  6 8 de 160 5 120 8 3 5 de 200 5 120 de chocolate 200 2 120 5 80 de fresa Ha cocinado más de chocolate. 9 20 3 5 5 100 100 : 20 5 5 20 1 5 5 25 Tuvo que pagar 25 €. 10  3 7 , 3 4 Ha pintado más Laura. 11 15.000 : 6 5 2.500 2.500 : 8 c 5 312, r 5 4 Se han obtenido 312 paquetes y han sobrado 4 cajas. 12 25.000 2 1.800 5 23.200 23.200 : 50 5 464 Obtuvieron 464 sacos. 13 1 5 de 180 5 36 36 : 2 5 18 Vienen en bicicleta 18 chicas. Notas Repaso en común • Reúna a los alumnos en pequeños grupos y pida a cada uno de ellos que proponga en una hoja distintas actividades relacionadas con los contenidos tratados en la unidad. Pueden ayudarse de las planteadas en el libro de texto. Un grupo trabajará las unidades decimales, otro los números decimales, otro la comparación y otro las aproximaciones. Después, reúna todas las hojas y entregue a cada alumno un cuaderno de repaso formado por todas ellas para que practique. Resuelva algunas de ellas, las que susciten mayores dificultades, en común. 39
Operaciones con números decimales88 Contenidos de la unidad SABER NÚMEROS Y OPERACIONES • Suma de números decimales. •  Resta de números decimales. •  Multiplicación de números decimales. SABER HACER NÚMEROS Y OPERACIONES • Cálculo de sumas de números decimales y de fracciones decimales. • Cálculo de restas de números decimales y de fracciones decimales. • Cálculo de operaciones combinadas de sumas y restas de decimales. • Multiplicación de números decimales. • Multiplicación de un número decimal por un natural y por la unidad seguida de ceros. • Resolución de problemas utilizando la suma, resta y multiplicación de números decimales. RESOLUCIÓN DE PROBLEMAS • Escritura de un problema obteniendo los datos de su resolución. • Invención de un problema utilizando unas palabras y unos cálculos.   TAREA FINAL • Revisar una factura. FORMACIÓN EN VALORES • Valoración de las operaciones con decimales para la resolución de situaciones reales. • Interés por la resolución de problemas. 40
BIBLIOTECA DEL PROFESORADO Programación didáctica de aula Recursos para la evaluación • Evaluación de contenidos. Unidad 8: pruebas de control B y A. • Evaluación por competencias. Prueba 8. •  Rúbrica. Unidad 8. Enseñanza individualizada • Plan de mejora. Unidad 8. • Programa de ampliación. Unidad 8. Proyectos de trabajo cooperativo • Proyecto del segundo trimestre. Recursos complementarios • Fichas para el desarrollo de la inteligencia. • Operaciones y problemas. Aprendizaje eficaz • Técnicas de estudio y presentación de exámenes. Proyectos interdisciplinares • Programa de Educación en valores. • Programa de Educación emocional. • Inteligencias múltiples. RECURSOS DIGITALES LibroMedia • Unidad 8: actividades y recursos. MATERIAL DE AULA Láminas OTROS MATERIALES DEL PROYECTO Cuaderno del alumno • Segundo trimestre. Unidad 8. Solución de problemas. Método DECA SUGERENCIA DE TEMPORALIZACIÓN Enero MarzoFebrero ES0000000024590 663006_Matematicas_4_GRAZ_24259 PRIMARIA PRIMARIA Matemáticas PRIMARIA ANDALUCÍAMatemáticas ANDALUCÍA Matemáticas ANDALUCÍA ES0000 000024 590 663006 _Matem aticas_4_GRA Z_2425 9.indd 1 04/03/2 015 11:21:19 ES0000000024593 663039_Cdno_Matematicas_4-2_22732 PRIMARIA Matemáticas Segundo trimestre Matemáticas Segundo trimestre PRIMARIA CUADERNO CUADERNO ES0000000024593 663039_Cdno_Matematicas_4-2_22732.indd 1 19/02/2015 16:56:18 41
8 Operaciones con números decimales La olimpíada de primavera Cada año en el colegio, cuando llega la primavera, celebran su propia olimpíada. Se realizan muchas pruebas y todos tienen la oportunidad de participar en ellas. Una de las más famosas es la vuelta al colegio. ¡Está tan disputada que tienen que medir los tiempos en décimas de segundo! Tiempos en la vuelTa al ColeGio mario 23,8 s Teresa 23,4 s andrés 24,6 s mercedes 24,2 s 112 ES0000000024590 663006-Unidad 08_22591.indd 112 10/03/2015 13:16:31 TiEMPOs En LA vUELTA AL COLEGiO Mario 23,8 s Teresa 23,4 s Andrés 24,6 s Mercedes 24,2 s Propósitos •  Reconocer situaciones reales en las que se utilicen números decimales. •  Recordar los conceptos básicos necesarios para el desarrollo de la unidad. Previsión de dificultades •  Algunos alumnos pueden tener dificultad en la colocación de los números decimales para calcular sumas y restas cuando los números tienen distinto número de cifras decimales. Ayúdeles explicando   que las comas de los números decimales deben estar en la misma columna y la coma del resultado estará siempre colocada debajo   de ellas. •  Vigile que los alumnos colocan correctamente la coma en   el resultado de los productos al multiplicar decimales. En ocasiones lo suelen olvidar o colocar mal. Pídales que razonen a menudo cuántas cifras deben separar   con la coma. Trabajo colectivo sobre la lámina Lea la situación planteada y pida   a los alumnos que lean en el cuadro   el tiempo que tardó cada niño en dar la vuelta al colegio. Pídales que recuerden cómo se leen esos números, qué partes tienen, cuál   es el valor de cada cifra… 1   Mario: 23,8 s. Parte entera: 23. Parte decimal: 8. 2   Menos de 24 s: Mario y Teresa. Más de 23,9 s: Andrés   y Mercedes. 3   Recuerde a los alumnos, si es necesario, cómo se comparan números decimales.  23,4 , 23,8 , 24,2 , 24,6 4   R. M.      24,3      24,4      24,5  Si lo cree conveniente puede explicar a los alumnos que entre dos números decimales hay infinitos números decimales. Otras formas de empezar •  Pida a los alumnos que expresen oralmente situaciones reales   en las que se utilizan números decimales y que pongan algunos ejemplos. Pregunte por qué creen que son necesarios en esas situaciones los números decimales y que expliquen los inconvenientes que habría si no se pudieran utilizar. Aporte algunos ejemplos de contextos en los que sea necesario sumarlos, restarlos o multiplicarlos y pida a los alumnos que aporten otros ellos mismos. 42
1 ¿Qué número expresa el tiempo que tardó Mario? ¿Cuál es su parte entera? ¿Y su parte decimal? 2 ¿Quiénes tardaron menos de 24 segundos en la vuelta al colegio? ¿Y más de 23,9 segundos? 3 Ordena los cuatro tiempos de menor a mayor. 4 EXPRESIÓN ORAL. Di dos tiempos que sean mayores que el de Mercedes pero menores que el de Andrés. Explica cómo los has obtenido. Lee, comprende y razona Números decimales: lectura y descomposición Los números decimales tienen una parte entera, a la izquierda de la coma, y una parte decimal, a la derecha de la coma. Parte entera: 13. Parte decimal: 75. Lectura: 13 unidades y 75 centésimas o 13 coma 75. Descomposición: 1 decena 1 3 unidades 1 7 décimas 1 5 centésimas 1 D 1 3 U 1 7 d 1 5 c 10 1 3 1 0,7 1 0,05 1 Escribe cómo se lee cada número y su descomposición. 3,9 18,36 27,04 6,198 2,031 11,005 Comparación de números decimales Para comparar números decimales, primero compara sus partes enteras; si son iguales, compara las décimas; si también lo son, las centésimas, y así sucesivamente. 2 Compara cada pareja de números. 6,75 y 7 8,36 y 8,39 7,042 y 7,03 5,003 y 5,011 ¿Qué sabes ya? TAREA FINAL Revisar una factura Al final de la unidad revisarás si una factura es correcta. Antes, aprenderás a sumar, restar y multiplicar números decimales. SABER HACER 3,82 , 4 7,16 . 7,12 9,325 , 9,328 13,75 113 ES0000000024590 663006-Unidad 08_22591.indd 113 10/03/2015 13:16:33 UNIDAD 8 ¿Qué sabes ya? Asegúrese de que los alumnos dominan los procedimientos de lectura, escritura, descomposición y comparación de decimales ya que son muy importantes para que aborden con éxito la unidad. 1   •  3 unidades y 9 décimas 3 1 0,9 •  18 unidades y 36 centésimas 10 1 8 1 0,3 1 0,06 •  27 unidades y 4 centésimas 20 1 7 1 0,04 •  6 unidades y 198 milésimas 6 1 0,1 1 0,09 1 0,008 •  2 unidades y 31 milésimas 2 1 0,03 1 0,001 •  11 unidades y 5 milésimas 10 1 1 1 0,005 2   •  6,75 , 7 •  8,36 , 8,39 •  7,042 . 7,03 •  5,003 , 5,011 Notas Competencias •  Comunicación lingüística. Al realizar las actividades propuestas después de la lectura es importante que los alumnos utilicen correctamente el lenguaje matemático para expresarse. Anímelos a ser correctos y compruebe que lo hacen de forma clara. •  Aprender a aprender. Señale que el aprendizaje es un proceso continuo y que después de estudiar los números decimales en la unidad anterior van a seguir aprendiendo sobre ellos; ahora van a aprender a sumarlos, restarlos y multiplicarlos. Inteligencia lingüística 43
Suma de números decimales 1 Copia en tu cuaderno y calcula. 2 Coloca los números y calcula. 7,8 1 2,9 27,6 1 3,905 14,29 1 21,84 12,667 1 4,82 6,075 1 8,399 9,66 1 96,553 3 Piensa y contesta. Si sumas dos números con dos cifras decimales que sean menores que 10, ¿cuál es el valor máximo que puede tener esa suma? Michi pesa 15,78 kg y su cría, Sol, pesa 9,6 kg. ¿Cuántos kilos pesan los dos juntos? Suma 15,78 y 9,6 1.º Coloca un número debajo del otro, de forma que coincidan en la misma columna las cifras del mismo orden. D U d c 1 5, 7 8 1 9, 6 2.º Suma como si fueran números naturales y escribe una coma en el resultado, debajo de la columna de las comas. D U d c 1 5, 7 8 1 9, 6 2 5, 3 8 Los dos juntos pesan 25,38 kg. Para sumar números decimales, se colocan de forma que coincidan en la misma columna las cifras del mismo orden. Después, se suman como si fueran números naturales y se coloca una coma en el resultado debajo de la columna de las comas. D U d c 1 5, 7 8 1 3 2, 0 7 D U d c m 7 6, 9 1 8 4, 6 5 2 C D U d c 4 2 9, 6 1 7 8, 7 4 PRESTA ATENCIÓN Fíjate en que las comas de ambos números estén en la misma columna. Pon la coma en el resultado. 9,6 15,78 114 ES0000000024590 663006-Unidad 08_22591.indd 114 10/03/2015 13:16:35 Propósitos •  Sumar dos o más números decimales. •  Resolver problemas de sumas   de números decimales. Sugerencias didácticas Para explicar. Lea la situación planteada y pregunte a los alumnos qué operación hay que realizar para resolverla. Escriba la suma correspondiente en la pizarra   y resuélvala explicando los pasos que hay que seguir. Haga especial hincapié en la colocación de los números decimales. Señale que en las sumas la coma del resultado quedará colocada bajo las comas de los sumandos. Para reforzar. Pregunte a los alumnos cómo sumarían un número natural y un decimal. Hágales ver que podemos considerar a los números naturales como números decimales sin parte decimal. Actividades 1   •  47,85 •  161,552 •  508,34 2   •  10,7 •  31,505 •  36,13 •  17,487 •  14,474 •  106,213 3   Pregúnteles cuál es el mayor número decimal con 2 cifras decimales menor que 10. Deles un tiempo para pensar y hágales ver que ese número es 9,99 y, por tanto, el máximo valor de la suma será 19,98. 4   •  (2,6 1 3,5) 1 4,8 5 10,9  2,6 1 (3,5 1 4,8) 5 10,9 •  (8,25 1 1,9) 1 6,74 5 16,89 8,25 1 (1,9 1 6,74) 5 16,89 •  (0,372 1 1,6) 1 2,88 5 4,852 0,372 1 (1,6 1 2,88) 5 4,852 5   •  0,8 1 0,36 5 1,16 •  0,178 1 0,9 5 1,078 •  0,71 1 0,071 5 0,781 •  0,6 1 0,806 5 1,406 Otras actividades •  Forme grupos de tres alumnos y haga que cada grupo prepare cinco tarjetas con estos números decimales. Pida a cada grupo que ponga las tarjetas boca abajo y cada alumno,   por turno, cogerá dos tarjetas y calculará la suma correspondiente, volviendo a dejar las dos tarjetas en el montón. Después, haga que comparen los resultados obtenidos y ganará el alumno que haya obtenido la suma mayor. 2,75 0,469 8,53 9,732 46,8 44
8 4 Suma cada grupo de tres números de dos formas cambiando el orden de los sumandos. ¿Obtienes el mismo resultado? ¿Por qué crees que ocurre? 5 Suma estas fracciones. Exprésalas primero en forma de número decimal. 8 10 1 36 100 178 1.000 1 9 10 71 100 1 71 1.000 6 10 1 806 1.000 Problemas 6 Resuelve. Un gato pesa 5,2 kg, una tortuga 1,78 kg y un loro 0,625 kg. – ¿Cuánto pesan juntos el gato y la tortuga? ¿Y la tortuga y el loro? – ¿Cuánto pesan los tres animales juntos? Un caracol trepó tres días por una pared. El primer día trepó 2,78 m, el segundo día 4,5 m y el tercero 5,81 m. ¿Qué distancia trepó en total? Lidia sacó en dos exámenes 8,5 puntos y 6,78 puntos, respectivamente. Nadia sacó 8,71 puntos y 6,59 puntos en los mismos exámenes. ¿Quién sacó más puntuación total? Miguel pesa 42,75 kg y su hermana Eva pesa 1,8 kg más que él. ¿Cuántos kilos pesan los dos juntos? Suma 11 a un número: primero suma 10 y luego suma 1 37 1 11 213 1 11 1.872 1 11 45 1 11 562 1 11 3.624 1 11 58 1 11 718 1 11 6.513 1 11 69 1 11 849 1 11 9.129 1 11 CÁLCULO MENTAL 2,6 1 3,5 1 4,8 0,372 1 1,6 1 2,88 8,25 1 1,9 1 6,74 EJEMPLO 8 10 1 36 100 5 0,8 1 … 5 … 347 357 358 1 10 1 1 1 11 115 ES0000000024590 663006-Unidad 08_22591.indd 115 10/03/2015 13:16:36 UNIDAD 8 6   •  El gato y la tortuga: 5,2 kg 1 1,78 kg 5 6,98 kg La tortuga y el loro: 1,78 kg 1 0,625 kg 5 2,405 kg Los tres juntos: 5,2 kg 1 1,78 kg 1 0,625 kg 5 5 7,605 kg •  2,78 1 4,5 1 5,81 5 13,09 En total trepó 13,09 metros. •  Lidia: 8,5 1 6,78 5 15,28 Sacó 15,28 puntos. Nadia: 8,71 1 6,59 5 15,30 Sacó 15,30 puntos. Sacó más puntuación Nadia. •  42,75 1 1,8 5 44,55 42,75 1 44,55 5 87,30 Los dos juntos pesan 87,30 kg. Cálculo mental •  48 •  224 •  1.883 •  56 •  573 •  3.635 •  69 •  729 •  6.524 •  80 •  860 •  9.140 Notas Otras actividades •  Pida a cada alumno que complete una ficha con su nombre, su altura en metros y su peso en kilos. A continuación, haga grupos de tres alumnos y pídales que calculen actividades similares a las siguientes: –  La altura total de los dos más altos. –  El peso total de los dos de menor peso. –  La altura total de los tres. –  El peso total de los tres. 45
Resta de números decimales 1 Coloca los números y calcula. 9,6 2 1,9 27,16 2 3,9 23,5 2 3,76 18,91 2 4,675 4,8 2 1,999 8,4 2 2,067 2 Calcula el término que falta en cada caso. ★ 1 2,5 5 3 ★ 2 1,28 5 4 ★ 1 1,3 5 2,6 ★ 2 3,6 5 5,889 6,72 1 ★ 5 9,126 11,2 2 ★ 5 8,88 1,8 1 ★ 5 4,675 9,75 2 ★ 5 2,6 En la prueba de salto de longitud, Mario ha saltado 4,75 m y Olga ha saltado 5,2 m. ¿Cuánto ha saltado Olga más que Mario? Resta 5,2 2 4,75 1.º Coloca un número debajo del otro, de forma que las comas concidan. Añade ceros si faltan cifras decimales. U d c 5, 2 0 2 4, 7 5 2.º Resta como si fueran números naturales y escribe una coma en el resultado debajo de la columna de las comas. U d c 5, 2 0 2 4, 7 5 0, 4 5 Olga ha saltado 0,45 m más que Mario. Para restar números decimales, se colocan de forma que coincidan en la misma columna las cifras del mismo orden. Se añaden ceros si faltan cifras decimales y, después, se resta como si fueran números naturales. Luego se coloca la coma en el resultado. PRESTA ATENCIÓN Coloca ceros en los lugares en los que falten cifras decimales. EJEMPLO ★ 5 3 2 2,5 5 0,5 EJEMPLO ★ 5 4 1 1,28 5 5,28 116 ES0000000024590 663006-Unidad 08_22591.indd 116 10/03/2015 13:16:37 Propósitos •  Restar números decimales. •  Resolver situaciones de resta. Sugerencias didácticas Para explicar. Pida a un alumno   que lea la situación propuesta   y pregúnteles qué operación hay que realizar para resolverla. Escriba   la resta correspondiente en la pizarra explicando que, cuando los números decimales tienen distinto número   de cifras decimales, completamos   con ceros. Muestre la similitud con   la suma al colocar los términos. Para reforzar. Escriba en la pizarra varias restas de números decimales con distinto número de cifras decimales, y pídales que coloquen   los números para restarlos y completen con los ceros necesarios. Después, calcularán esas restas. Pregúnteles cómo realizarían la resta de un número decimal y un natural,   y trabaje algún ejemplo en común. Actividades 1   •  7,7 •  23,26 •  19,74 •  14,235 •  2,801 •  6,333 2   •  5 3 2 2,5 5 0,5 •  5 2,6 2 1,3 5 1,3 •  5 9,126 2 6,72 5 2,406 •  5 4,675 2 1,8 5 2,875 •  5 4 1 1,28 5 5,28 •  5 5,889 1 3,6 5 9,489 •  5 11,2 2 8,88 5 2,32 •  5 9,75 2 2,6 5 7,15 3   •  6,1 2 1,89 5 4,21 •  5,42 1 6,7 5 12,12 •  7,2 2 0,667 5 6,533 •  5 1 0,61 5 5,61 •  8,21 2 0,11 5 8,10 •  9,6 2 1,733 5 7,867 4   •  0,5 2 0,12 5 0,38 •  0,45 2 0,009 5 0,441 •  0,7 2 0,002 5 0,698 •  0,06 2 0,004 5 0,056 Otras actividades • Pida que cada alumno escriba en su cuaderno tres números decimales   con una, dos y tres cifras decimales respectivamente, y calcule todas   las restas posibles con los números que ha escrito. Haga que un alumno salga a la pizarra y escriba los números que   ha escrito y las restas correspondientes. Entre todos se comprobará   si la solución dada es o no correcta. Puede repetir el proceso con varios alumnos. 46
8 RAZONAMIENTO Problemas 5 Resuelve. Manuel ha comprado 7,5 kg de manzanas, 4,92 kg de peras y 1,925 kg de plátanos. ¿Cuánto pesan las manzanas más que las peras? ¿Y los plátanos menos que las manzanas? Ruth corrió tres veces los 100 m lisos. La primera vez tardó 15,2 s, la segunda vez 0,4 s menos que la primera y la tercera vez 0,38 s menos que la segunda. ¿Cuánto tardó la tercera vez? Andrés pesa 57,50 kg y su prima Ana pesa 9,8 kg menos que él. ¿Cuántos kilos pesan los dos juntos? Lola tenía 40 €. Gastó 8,93 € en un pañuelo y 12,79 € en unos pendientes. ¿Cuánto dinero le quedó? 3 Halla el resultado de estas expresiones. Sigue el mismo orden que en las operaciones combinadas con números naturales. 2,5 1 3,6 2 1,89 5 1 (2,6 2 1,99) 8,42 2 3 1 6,7 8,21 2 (5 2 4,89) 9,6 2 2,4 2 0,667 9,6 2 (2,4 2 0,667) 4 Resta estas fracciones. Exprésalas primero en forma de número decimal. 5 10 2 12 100 45 100 2 9 1.000 7 10 2 2 1.000 6 100 2 4 1.000 RECUERDA 1.º Operaciones de los paréntesis. 2.º Sumas y restas en el orden en el que aparecen. 117 Piensa y contesta. Pon ejemplos si es necesario. La suma de dos números decimales ¿puede ser un número natural? ¿Y la resta de dos números decimales? Si restas dos números decimales con dos cifras en su parte decimal, ¿puedes obtener otro con una sola cifra decimal? 2,3 1,49 8,278 ES0000000024590 663006-Unidad 08_22591.indd 117 10/03/2015 13:16:38 UNIDAD 8 5   •  7,5 2 4,92 5 2,58 Las manzanas pesan 2,58 kg más que las peras. 7,5 2 1,925 5 5,575 Los plátanos pesan 5,575 kg menos que las manzanas. •  15,2 2 0,4 5 14,8 14,8 2 0,38 5 14,42 La tercera vez tardó 14,42 s. •  57,50 2 9,8 5 47,70 57,50 1 47,70 5 105,20 Los dos juntos pesan 105,20 kg. •  8,93 1 12,79 5 21,72 40 2 21,72 5 18,28 Le quedaron 18,28 €. Razonamiento •  Sí, la suma y la resta de dos números decimales puede ser un número natural. Basta con que sean iguales o bien que sumen una unidad. Ejemplos: 12,65 1 3,35 516 34,56 2 9,56 5 25 •  Sí, basta con que sus cifras de las centésimas sean iguales. Ejemplo: 14,25 2 6,75 5 7,50 Notas Otras actividades •  Prepare un dado pegando en sus caras pegatinas, de forma que haya dos caras con un 1, otras dos con un 2 y otras dos con un 3. Lance el dado y pida a un alumno que diga un número decimal cuyo número de cifras decimales sea el que haya salido en el dado. Escríbalo en la pizarra. Repita el proceso para obtener otro número y pida a los alumnos que sumen y resten los dos números escritos. •  Puede pedir a los alumnos que investiguen si la suma de decimales cumple las propiedades conmutativa y asociativa. Con la resta, puede pedirles que hagan la prueba de las restas que realicen. 47
Multiplicación de números decimales 1 Calcula en tu cuaderno. No olvides colocar la coma en su lugar correcto. 3,5 3 1,6 0,36 3 9,2 3,012 3 5,4 25,167 3 3,8 2,18 3 4,7 1,7 3 37,88 2,3 3 0,194 4,7 3 1,006 2 Escribe con cifras y calcula. Seis unidades y nueve centésimas por tres unidades y doce milésimas. Cuarenta y ocho coma dos por diecisiete coma treinta y seis. 3 Calcula estos productos de un número decimal por un número natural. 3,7 3 9 9,25 3 7 6,174 3 6 8,75 3 12 6,789 3 34 Teresa ha comprado 4,6 kg de naranjas para hacer zumo. Cada kilo cuesta 1,25 €. ¿Cuánto han costado en total? Multiplica 1,25 por 4,6 1.º Multiplica los números como si fueran números naturales. 2.º En el resultado, separa con una coma, a partir de la derecha, tantas cifras decimales como tengan en total los dos factores. Las naranjas han costado 5,75 €. Para multiplicar dos números decimales, se multiplican como si fueran números naturales, y en el resultado se separan, con una coma, a partir de la derecha, tantas cifras decimales como tengan en total los dos factores. 1, 2 5 3 4, 6 7 5 0 5 0 0 5 7 5 0 HAZLO ASÍ 1, 2 5 3 4, 6 7 5 0 5 0 0 5, 7 5 0 2 cifras decimales 1 cifra decimal 2 1 1 5 3 3 cifras decimales Considera el número natural como un número decimal sin cifras decimales. 3 3 5,61 5 16,83 2 cifras decimales 118 ES0000000024590 663006-Unidad 08_22591.indd 118 10/03/2015 13:16:39 Propósitos •  Multiplicar números decimales. •  Resolver situaciones   de multiplicación. Sugerencias didácticas Para explicar. Haga que un alumno lea la situación planteada y pregúnteles la operación que debemos calcular para resolverla. Resuelva la multiplicación correspondiente en la pizarra, explicando el procedimiento que hay que seguir. Haga especial hincapié   en la colocación de la coma en el resultado. Deje claro que en este caso la coma del resultado no se coloca bajo la coma de los términos, como   sí que ocurría en la suma y la resta. Pregúnteles a menudo dónde va la coma colocada para que interioricen este procedimiento. Comente los casos particulares de   los productos por números naturales   y por la unidad seguida de ceros. Para reforzar. Puede escribir en   la pizarra varias multiplicaciones   de números decimales y preguntar   a los alumnos cuántas cifras decimales tendrá cada resultado. Actividades 1   •  5,6 •  16,2648 •  10,246 •  0,4462 •  3,312 •  95,6346 •  64,396 •  4,7282 2   •  6,09 3 3,012 5 18,34308 •  48,2 3 17,36 5 836,752 3   •  33,3 •  64,75 •  37,044 •  105 •  230,826 4   •  30,7 •  137 •  28 •  13,4 •  276,15 •  2.800 •  620 •  4.670 5   •  0,012 3 100 5 1,2 m  La fila mide 1,2 m. Otras actividades •  Pida a los alumnos que confeccionen tablas similares a la siguiente,   y que se las intercambien entre ellos para resolverlas. Cada uno deberá después comprobar la corrección de los resultados   de su compañero. 3 3 3 5 3 7 3 10 3 100 3 1.000 2,38 7,3 7,982 0,097 3,42 48
8 4 Multiplica cada número decimal por la unidad seguida de ceros. 3,07 3 10 2,8 3 10 27,615 3 10 6,2 3 100 1,37 3 100 0,134 3 100 2,8 3 1.000 4,67 3 1.000 Problemas 5 Resuelve. Cien hormigas se han colocado en fila. Cada una de ellas mide 0,012 m. ¿Cuántos metros mide en total la fila de hormigas? Marta compró una piña por 2,75 € y 1,4 kg de fresas que costaban 2,80 € el kilo. ¿Cuánto pagó Marta por su compra? Un tren lleva 10 vagones, que miden 7,8 m cada uno, y una locomotora, que mide 2,6 m más que un vagón. ¿Cuál es la longitud total del tren? En una tienda tienen 100 paquetes de zumo de 0,25 ℓ cada uno y 32 botellas de 1,5 ℓ. ¿Cuántos litros de zumo tienen en total en la tienda? HAZLO ASÍ Para multiplicar un número decimal por la unidad seguida de ceros se desplaza la coma a la derecha tantos lugares como ceros siguen a la unidad. Si es necesario, se añaden ceros. 12,45 3 10 5 124,5 9,8 3 100 5 980 1 cero 1 lugar 2 ceros 2 lugares a la derecha a la derecha Suma 9 a un número: primero suma 10 y luego resta 1 CÁLCULO MENTAL 27 1 9 213 1 9 1.345 1 9 48 1 9 342 1 9 2.068 1 9 56 1 9 781 1 9 7.612 1 9 75 1 9 864 1 9 9.601 1 9 347 357 356 1 10 2 1 1 9 119 ES0000000024590 663006-Unidad 08_22591.indd 119 10/03/2015 13:16:40 UNIDAD 8 • 1,4 3 2,80 5 3,92 2,75 1 3,92 5 6,67 Marta pagó 6,67 €. • 7,8 1 2,6 5 10,4 m 7,8 3 10 5 78 m 10,4 1 78 5 88,4 m La longitud del tren es 88,4 m. • 0,25 3 100 5 25 32 3 1,5 5 48 48 1 25 5 73 Tienen un total de 73 litros. Cálculo mental •  36 •  222 •  1.354 •  57 •  351 •  2.077 •  65 •  790 •  7.621 •  84 •  873 •  9.610 Notas Otras actividades •  Pida a los alumnos que inventen problemas que se resuelvan con una multiplicación de un decimal por un natural o multiplicando dos decimales. Después, los intercambiarán con sus compañeros y cada uno resolverá el problema creado por el otro. Más tarde, cada alumno comprobará si su problema fue bien resuelto. Póngales algunos ejemplos para ayudarlos si lo estima oportuno: – La ruta de un conductor de autobús es de 12,75 km. ¿Cuántos kilómetros recorre diariamente si cada día hace la misma ruta 9 veces? ¿Cuántos kilómetros recorrerá a la semana? Inteligencia naturalista 49
Escribe en tu cuaderno cada problema y completa los datos que faltan teniendo en cuenta su resolución. 1 Nieves compró un libro por €. También compró un disco, algo más caro, por €. Pagó con €. ¿Cuánto dinero le quedó? 2 Miguel envasó avellanas en bolsas de kg. Envasó kg y vendió bolsas. ¿Cuántas bolsas no pudo vender? 3 Luna vendió varias sandías a € cada una. Había recogido , pero de ellas estaban estropeadas. ¿Cuánto dinero obtuvo? Vamos a leer el problema y su resolución. Después, completaremos los datos que faltan en el enunciado a partir de esa resolución. Ramón compró un abrigo por €. Tenía varios billetes de € y pagó con de ellos. ¿Cuánto dinero le devolvieron? Al leer el problema sabemos que pagó una cantidad mayor que el precio del abrigo. Además, los billetes tienen que ser de 20 €, viendo los números que aparecen en los cálculos. Ramón compró un abrigo por 75 €. Tenía varios billetes de 20 € y pagó con 4 de ellos. ¿Cuánto dinero le devolvieron? Extraer datos de la resolución de un problema Solución de problemas Resolución 50 2 12 5 38 38 2 10 5 28 Resolución 50 2 8 5 42 42 3 4 5 168 Resolución 240 : 5 5 48 48 2 19 5 29 Resolución 4 3 20 5 80 80 2 75 5 5 120 ES0000000024590 663006-Unidad 08_22591.indd 120 10/03/2015 13:16:42 Propósitos •  Completar problemas extrayendo los datos de la resolución. •  Inventar problemas utilizando determinadas palabras y que se resuelvan con unos cálculos dados. Sugerencias didácticas Para explicar. Comente a los alumnos que en el enunciado   del problema faltan algunos datos   y señale que debemos completarlos obteniéndolos a partir de los cálculos de su resolución. Indíqueles que los primeros huecos   en el enunciado no corresponden necesariamente a los primeros datos de los cálculos. Deje que los alumnos vayan aportando sus propuestas, analizando la corrección de cada   una de ellas. Muestre la necesidad   de determinar si el enunciado obtenido tiene sentido y si se resuelve con los cálculos dados. Actividades 1   Nieves compró un libro por   10 €. También compró un disco algo más caro, por 12 €.   Pagó con 50 €. ¿Cuánto dinero   le quedó? 2   Miguel envasó avellanas en bolsas de 5 kg. Envasó 240 kg y vendió 19 bolsas. ¿Cuántas bolsas   no pudo vender? 3   Luna vendió varias sandías a 4 € cada una. Había recogido 50, pero 8 de ellas estaban estropeadas. ¿Cuánto dinero obtuvo? 4   Leonor compró una lavadora   que costaba 455 €. Pagó con   9 billetes de 50 € y un billete   de 5 €. ¿Cuánto dinero   le devolvieron? 5   A una excursión se apuntaron   130 hombres, pero se borraron 45 (o 20). Se apuntaron más mujeres que hombres, 150 mujeres,   y se borraron 20 (o 45). ¿Cuántas personas fueron al final? Otras actividades •  Agrupe a los alumnos y pida a cada grupo que escriba un problema   y lo resuelva. Después, en una hoja aparte, escribirán el enunciado   quitando los datos y, debajo de él, los cálculos que han usado   para resolverlo. Lo pasarán a otro grupo que intentará reconstruirlo.   Una vez hecho, cada grupo comprobará el desempeño de sus compañeros. Comente algunas de las propuestas y sus resoluciones en común. 50
Fíjate en cada grupo de palabras y cálculos, y escribe en tu cuaderno un problema en el que los utilices. adultos niños precio entrada 87 3 4 5 348 95 3 9 5 855 348 1 855 5 1.203 dinero compró repartió sobrinos 600 2 40 5 560 560 : 7 5 80 8 Fíjate en cada resolución y escribe el enunciado completo en tu cuaderno. 4 Leonor compró una lavadora que costaba €. Pagó con billetes de €, y un billete de €. ¿Cuánto dinero le devolvieron? 5 A una excursión se apuntaron hombres, pero se borraron . Se apuntaron más mujeres que hombres, mujeres, y se borraron . ¿Cuántas personas fueron al final? INVENTA TUS PROBLEMAS Fíjate en cada grupo de palabras y cálculos, y escribe en tu cuaderno un problema en el que los utilices. Resolución 600 : 2 5 300 300 : 5 5 60 60 3 4 5 240 6 Paula repartió en partes iguales las patatas que tenía. Envasó una parte en bolsas de kg y vendió cada bolsa a €. Si tenía kg de patatas, ¿cuánto dinero obtuvo? Resolución 9 3 50 5 450 450 1 5 5 455 455 2 453 5 2 Resolución 130 1 150 5 280 45 1 20 5 65 280 2 65 5 215 vendió 275 2 18 5 257 257 3 3 5 771 manzanas estropeadas 121 ES0000000024590 663006-Unidad 08_22591.indd 121 10/03/2015 13:16:44 UNIDAD 8 6 Paula repartió en 2 partes iguales las patatas que tenía. Envasó una parte en bolsas de 5 kg cada una y vendió cada bolsa a 4 €. ¿Cuánto dinero obtuvo? Inventa tus problemas •  R. M. Ricardo recogió 275 kg de manzanas. Tiró 18 kg que estaban estropeadas y vendió cada kilo a 3 €. ¿Cuánto dinero obtuvo Ricardo por la venta? •  R. M. Julia cobró un cheque de 600 €. Compró un sillón por 40 € y el resto lo repartió en partes iguales entre sus 7 sobrinos. ¿Cuánto dinero dio a cada uno? •  R. M. A una película de estreno asistieron 87 niños y 95 adultos. Cada entrada de niño costaba 4 € y la de adulto 9 €. ¿Cuánto se recaudó en total? Notas Competencias •  Iniciativa y emprendimiento. Las actividades de invención de problemas son un contexto muy adecuado para desarrollar esta competencia. Pida a los alumnos que lean detenidamente las palabras y los cálculos de la primera situación y expongan oralmente sus propuestas. Entre todos se comprobará si son o no correctas. Más tarde, déjeles que trabajen por sí mismos el resto de actividades y comente las diferentes aportaciones. Inteligencia interpersonal 51
14,16 8,75 11,3 13,45 112,9 29,05 27,165 3 100 3 4 7 Multiplica estos decimales. 2,8 3 3,9 9,21 3 3,87 4,28 3 5,36 3,6 3 2,84 2,725 3 1,4 4,2 3 4,35 8 Multiplica. 9 3 8,3 0,039 3 17 17,82 3 5 28 3 12,35 4 3 3,776 9,78 3 312 9 Multiplica cada uno de estos números por 10, por 100 y por 1.000. 10 Recuerda cómo se multiplica por la unidad seguida de ceros y halla el número que falta. 3 10 5 45 3 1.000 5 34 3 100 5 126,3 3 100 5 78 3 1.000 5 17 3 10 5 3,6 11 Calcula y completa en tu cuaderno. 12 Calcula y compara en tu cuaderno. 2,8 1 3,9 7 2 0,25 4,7 2 1,884 14,8 3 0,2 0,36 3 100 8,25 3 3,4 1 Suma estos números decimales. 3,9 1 2,75 0,86 1 2,99 1,667 1 2,4 6,57 1 8,075 9,28 1 0,997 15,4 1 16,803 2 Resta. 3,9 2 2,75 425,7 2 87,92 9,45 2 2,4 816,2 2 9,753 9,28 2 0,997 902,43 2 85,192 3 Piensa y contesta. María va a hacer todas las sumas y restas posibles con dos de estos tres números. Sin calcular, ¿qué suma dará un resultado mayor? ¿Qué resta dará un resultado menor? Calcula y comprueba tus respuestas. 4 Calcula el término que falta. Piensa si tienes que sumar o restar. 2 3,6 5 2,98 5,765 2 5 4,9 2 6,82 5 10,1 2,4 2 5 0,367 5 Calcula. 4,2 1 3,75 2 2,6 (4,6 2 2,94) 2 1 8,76 2 (2,4 2 1,77) 8,701 1 2,6 1 3 9,34 2 (8,6 1 0,13) 10 2 1,8 2 2,97 6 VOCABULARIO. Explica cómo se multiplican dos números decimales. ACTIVIDADES 6,75 9,127 4,8 8,4 3,16 0,025 15,7 26,04 9,102 122 ES0000000024590 663006-Unidad 08_22591.indd 122 10/03/2015 13:16:45 Propósitos •  Repasar los contenidos básicos   de la unidad. Actividades 1 •  6,65 •  3,85 •  4,067 •  14,645 •  10,277 •  32,203 2   •  1,15 •  337,78 •  7,05 •  806,447 •  8,283 •  817,238 3 Suma con el resultado mayor: 9,127 1 6,75 5 15,877  Resta con el resultado menor: 6,75 2 4,8 5 1,95 4 •  5 2,98 1 3,6 5 6,58 •  5 5,765 2 4,9 5 0,865 •  5 10,1 1 6,82 5 16,92 •  5 2,4 2 0,367 5 2,033 5 •  7,95 2 2,6 5 5,35 •  8,76 2 0,63 5 8,13 •  9,34 2 8,73 5 0,61 •  1,66 2 1 5 0,66 •  11,301 1 3 5 14,301 •  8,2 2 2,97 5 5,23 6 R. L. 7 •  10,92 •  35,6427 •  22,9408 •  10,224 •  3,815 •  18,27 8 •  74,7 •  0,663 •  89,1 •  345,8 •  15,104 •  3.051,36 9 •  8,4 F 84 F 840 F 8.400 •  3,16 F 31,6 F 316 F 3.160 •  0,025 F 0,25 F 2,5 F 25 •  15,7 F157 F 1.570 F15.700 •  26,04 F 260,4 F 2.604 F  F 26.040 •  9,102 F 91,02 F 910,2 F  F 9.102 10 •  5 4,5 •  5 0,034 •  5 1,263 •  5 0,78 •  5 0,017 •  5 0,36 11  •  14,16 2 17,61 2 10,445 •  11,3 2 2,25 2 9 •  8,75 2 21,65 2 2,165 Otras actividades • Plantee a los alumnos actividades para afianzar los contenidos estudiados   en la unidad. Puede proponer actividades de suma, resta y multiplicación   de números decimales como las que se indican a continuación. Suma 1,25 cada vez Resta 3,7 cada vez Multiplica por 0,2 cada vez 24,3 125 0,089 52
15 Resuelve. Jaime es repostero y tiene una receta secreta que usa para hacer la tarta de chocolate. ¿Cuántos kilos pesan en total la harina y el azúcar de una tarta? Si Jaime decide hacer 3 tartas, ¿cuántos kilos de mantequilla necesita? ¿Y de cacao? Para un encargo de 10 tartas, ¿cuántos kilos de azúcar necesita? ¿Y de harina? El mes pasado Jaime hizo 100 tartas de chocolate. ¿Gastó en ellas más o menos de 25 kg de mantequilla? ¿Cuántos kilos de cacao gastó? En un pedido de 8 tartas, ¿cuántos kilos más pesan la harina y la mantequilla que el azúcar y el cacao? Problemas 13 Resuelve. Jimena vende el metro de cordón a 3,40 €. Tenía un rollo de 10 m, vendió 1,85 m a un cliente y a otro cliente, el resto del rollo. ¿Cuánto pagó el segundo cliente? 14 Piensa y resuelve. Un modelo de coche gasta 7,26 ℓ de gasolina cada 100 km. ¿Cuánto gastará si recorre 500 km? ¿Y 1.000 km? Manuela medía 1,20 m. Creció 0,65 m y después 0,09 m. ¿Cuántos metros mide ahora Manuela? Carmen recogió 50 kg de peras. Guardó 7 kg para ella y vendió el resto a 3,75 € el kilo. ¿Cuánto dinero obtuvo? 15 Resuelve. Jaime es repostero y tiene una receta secreta que usa para hacer la tarta de chocolate. ¿Cuántos kilos pesan en total la harina y el azúcar de una tarta? Si Jaime decide hacer 3 tartas, ¿cuántos kilos de mantequilla necesita? ¿Y de cacao? Para un encargo de 10 tartas, ¿cuántos kilos de azúcar necesita? ¿Y de harina? El mes pasado Jaime hizo 100 tartas de chocolate. ¿Gastó en ellas más o menos de 25 kg de mantequilla? ¿Cuántos kilos de cacao gastó? En un pedido de 8 tartas, ¿cuántos kilos más pesan la harina y la mantequilla que el azúcar y el cacao? 8 16 ¿Cómo multiplicarías estas fracciones? Recuerda la relación entre decimales y fracciones. 7 10 3 2 10 3 100 3 5 10 9 10 3 6 100 Demuestra tu talento TARTA DE CHOCOLATE 0,2 kg de harina 0,25 kg de azúcar 0,24 kg de mantequilla 0,05 kg de cacao en polvo 1 sobre de levadura 6 huevos y canela 123 ES0000000024590 663006-Unidad 08_22591.indd 123 10/03/2015 13:16:46 UNIDAD 8 12 • 6,7 , 6,75 • 2,816 , 2,96 • 36 . 28,05 13 • (10 2 1,85) 3 3,40 5 27,71 € Pagó 27,71 €. 14 • 7,26 3 5 5 36,30 € 7,26 3 10 5 72,6 € Gastará 36,30 € en 500 km y 72,80 € en 1.000 km. • 1,20 1 0,65 1 0,09 5 1,94 Mide 1,94 m de altura. • (50 2 7) 3 3,75 5 161,25 Carmen obtuvo 161,25 €. 15 • 0,2 1 0,25 5 0,45 kg Pesan 0,45 kg. • 3 3 0,24 5 0,72 kg 3 3 0,05 5 0,15 kg Necesita 0,72 kg de mantequilla y 0,15 kg de cacao. • 0,25 3 10 5 2,5 0,2 3 10 5 2 Necesita 2,5 kg de azúcar y 2 kg de harina. • 0,24 3 100 5 24 Gastó menos de 25 kg de mantequilla (gastó 24 kg). 0,05 3 100 5 5 Gastó 5 kg de cacao. • 8 3 (0,2 1 0,24) 5 3,52 8 3 (0,25 1 0,05) 5 2,4 3,52 2 2,4 5 1,12 La harina y la mantequilla pesan 1,12 kg más. Demuestra tu talento 16  Expresamos cada fracción en forma de decimal y multiplicamos los decimales obtenidos. • 0,7 3 0,2 5 0,14 • 0,03 3 0,5 5 0,015 • 0,9 3 0,06 5 0,054 Notas Competencias • Competencia social y cívica. Realice en común, aprovechando el contexto de la actividad 15, un debate sobre temas relacionados con esta competencia: la importancia de una dieta sana, los derechos y deberes de los trabajadores, la necesidad de un consumo responsable… Pida a los alumnos que comenten sus ideas sobre estos temas y enuncien conductas positivas. 53
Revisar una factura Después de la olimpíada de primavera, el colegio organiza siempre una pequeña celebración para entregar los premios. Sergio, el director, está revisando los artículos que pidieron para la fiesta y la factura que le han enviado. 1 Observa la factura y resuelve. ¿Cuánto cuestan las botellas de zumo? ¿Cuánto cuestan las de agua? ¿Cuánto costaron las almendras y las patatas? ¿Cuánto costaron los bollitos? ¿Cuál fue el precio total de todos los artículos? Para hallar el precio a pagar hay que multiplicar el precio total por 1,21 ya que tenemos que añadir los impuestos. En la factura del supermercado Sergio ve que pone 174,63 €. ¿Está bien hecha? ¿Por qué? 2 TRABAJO COOPERATIVO. Resuelve con tu compañero. Para el año que viene, en el colegio han pensado comprar algunas cosas más para la fiesta. Quieren comprar 5 unidades más de cada artículo y cuentan con 200 € para la fiesta. ¿Tendrán bastante dinero? SABER HACER Artículo Unidades Precio unidad Botella de zumo 1,5 ℓ 10 2,75 Botella de agua 2 ℓ 30 0,79 Bolsa de almendras 8 3,37 Bolsa de patatas 20 1,42 Bolsa de bollitos 12 4,35 124 ES0000000024590 663006-Unidad 08_22591.indd 124 10/03/2015 13:16:49 Propósitos •  Desarrollar la competencia matemática resolviendo problemas de la vida cotidiana. •  Repasar contenidos clave. Actividades pág. 124 1 •  2,75 3 10 5 27,5   0,79 3 30 5 23,7  Zumo: 27,50 €.  Agua: 23,70 €. •  8 3 3,37 1 20 3 1,42 5 55,36 Almendras y patatas: 55,26 €. 4,35 3 12 5 52,2  Bollitos: 52,20 €. •  27,5 1 23,7 1 26,96 1 28,4 1 1 52,2 5 158,76  Precio total: 158,76 €. •  158,76 3 1,21 5 192,0996 € La factura no está bien hecha porque el total a pagar por el colegio, redondeando, es 192,10 €. 2 5 3 (2,75 1 0,79 1 3,37 1   1 1,42 1 4,35) 5 63,4  158,76 1 63,4 5 222,16 €  No tendrán suficiente con 200 € para la fiesta. Actividades pág. 125 1 •  300.089 •  6.100.004 •  2 6 •  3 8 •  9,02 •  19,015 2 •  3 CM 1 6 UM 1 7 C 1 1 D 1  1 5 U 5 300.000 1 6.000 1  1 700 1 10 1 5  Trescientos seis mil setecientos quince. •  8 U. de millón 1 1 CM 1 2 C 1  1 4 U 5 8.000.000 1 100.000 1  1 200 1 4  Ocho millones cien mil doscientos cuatro. •  7 U 1 9 d 1 4 c 5  5 7 1 0,9 1 0,04  7 unidades y 94 centésimas. •  1 D 1 2 U 1 7 d 1 6 m 5  5 10 1 2 1 0,7 1 0,006   12 unidades y 706 milésimas. Desarrollo de la competencia matemática •  En esta página los alumnos aplican las operaciones con decimales estudiadas en la unidad para resolver una situación de la vida real.  Es una situación próxima a ellos y que les resultará interesante. A la hora de abordar el trabajo cooperativo, pida a los alumnos que pongan por escrito cuál va a ser su modo de trabajo: qué van a calcular, por qué   y cómo van a realizar esos cálculos. Pídales también que calculen cuánto dinero necesitarán para la fiesta o cuántas unidades más de cada producto (o de algún producto en concreto) podrían comprar con el presupuesto   de 200 €. Inteligencia intrapersonal 54
4 Elimina los ceros que puedas y calcula cada división exacta. 2.500 : 50 63.000 : 900 3.600 : 600 28.000 : 40 5 Completa en tu cuaderno. 2 7 , 2 5 10 . 10 3 , 1 6 Compara. 11 5 2 4 31 8 15 7 3 7 Aproxima al orden indicado. Unidades 9,7 6,8 3,2 9,4 Décimas 9,36 8,21 7,48 Centésimas 5,132 9,278 1 Escribe con cifras. Trescientos mil ochenta y nueve. Seis millones cien mil cuatro. Dos sextos. Tres octavos. Nueve unidades y dos centésimas. Diecinueve coma cero quince. 2 Descompón cada número y escribe cómo se lee. 306.715 7,94 8.100.204 12,706 3 Calcula. 39.871 1 7.878 99.013 : 8 36.890 2 4.996 47.126 : 54 372 3 875 32.630 : 65 8 En salto de longitud, Jonás saltó 4,75 m, Elena 4,8 m y Lourdes 4,72 m. ¿Cuántos metros saltó el primer clasificado más que el último? 9 Los tres cuartos de una clase de 24 alumnos fueron a una ruta de senderismo. De ellos, la mitad eran chicas. ¿Cuántas chicas fueron a la ruta de senderismo? 10 En 4.º A todos deben leer un libro. Ana ha leído ya dos quintos, Silvia dos sextos y Juan tres quintos. ¿Quién ha leído más? 11 Al revisar 975 teléfonos móviles, se desecharon 14 por defectos. El resto se envió en paquetes de 31 teléfonos. ¿Cuántos paquetes se enviaron? 12 Los 12.000 socios de un club van a un partido en autobuses de 52 plazas. Cada uno cuesta 500 €. ¿Cuánto dinero han pagado? 13 ¿Cuánto cuestan 1.000 bolígrafos a 2,75 € cada uno? Problemas REPASO ACUMULATIVO 8 125 ES0000000024590 663006-Unidad 08_22591.indd 125 10/03/2015 13:16:50 UNIDAD 8 3 • 47.749 • c 5 12.376, r 5 5 • 31.894 • c 5 872, r 5 38 • 325.500 • c 5 502 4 • 50 • 70 • 6 • 700 5 R. M. •  2 7 , 2 5 •  5 10 . 1 10   •  2 3 , 1 6 •  11 5 . 2 •  4 . 31 8 •  15 7 , 3 7 • 10 • 7 • 3 • 9 • 9,4 • 8,2 • 7,5 • 5,13 • 9,28 8 4,8 2 4,72 5 0,08 Saltó 0,08 m más. 9 3 4 de 24 5 18; 18 : 2 5 9 Fueron a la ruta 9 chicas. 10 2 6 , 2 5 , 3 5 Ha leído más Juan. 11 975 2 14 5 961 961 : 31 5 31 Se enviaron 31 paquetes. 12 12.000 : 52 c 5 230, r 5 40 Necesitan 231 autobuses. 231 3 500 5 115.500 Han pagado 115.500 €. 13 2,75 3 1.000 5 2.750 Cuestan 2.750 €. Notas Repaso en común • Pida a los alumnos que realicen las actividades propuestas en esta página de forma individual y anoten aquellas en las que han tenido alguna dificultad para resolverlas. Comente con ellos por qué les han resultado más difíciles, y refuerce esas carencias resolviéndolas en común en la pizarra y proponiendo algunas más para asentar bien esos contenidos y avanzar con seguridad. 55
En el ambulatorio han representado en un gráfico de barras el número de personas atendidas del lunes al miércoles. Fíjate en cómo se interpreta. Gráficos de barras de tres características Tratamiento de la información 1 Observa el gráfico de arriba y contesta. ¿Cuántos adultos fueron atendidos el lunes? ¿Y niños? ¿Qué grupo fue el más numeroso el miércoles? ¿Y el lunes? ¿En qué días se atendió a más de 30 mayores? 2 Copia y completa el gráfico con los datos de las piezas de fruta que han comido esta semana tres amigos. Luis: 20 peras, 12 naranjas y 8 manzanas. Jon: 12 peras, 4 naranjas y 16 manzanas. María: 8 peras, 4 naranjas y 16 manzanas. Niños Adultos Mayores Número de personas Eje horizontal El miércoles atendieron a 50 mayores. Eje vertical Miércoles Martes Lunes 0 10 20 30 405 15 25 35 45 50 El martes, los adultos fueron el grupo más numeroso. Pera Naranja Manzana 24 20 16 12 8 4 0 Númerodepiezas Luis Jon María 126 ES0000000024590 663006-Unidad 08_22591.indd 126 10/03/2015 13:16:51 Gráficos de barras de tres característicasPropósitos •  Interpretar gráficos de barras   de tres características. •  Representar datos en gráficos   de barras de tres características. Sugerencias didácticas Para explicar. Haga que los alumnos observen el gráfico. Explíqueles cuál es el significado de cada barra de color y señale que para cada día tenemos información de las tres características. Trabaje en común algunas preguntas de interpretación, por ejemplo: ¿Cuántos niños fueron atendidos el martes? ¿En qué día atendieron a más adultos? ¿Entre   qué dos días aumentó el número   de adultos atendidos? Comente que para representar los gráficos debemos levantar una barra de la altura oportuna para cada característica. Trabaje la interpretación con el gráfico obtenido. Deje que los alumnos realicen por   sí solos el trabajo de recopilación   de datos y representación. Después, verifique que todos han obtenido   la misma gráfica e interprete,   de forma colectiva, los casos propuestos en el cuadro. 1 •  Adultos el lunes: 20.  Niños el lunes: 15. •  El miércoles: mayores.  El lunes: mayores. •  El lunes y miércoles. 2 3 a 5   R. L. Otras actividades •  Haga grupos de dos o tres alumnos y pídales que se fijen en el gráfico   del cuadro informativo y escriban varias frases que sean correctas a partir   de los datos representados. Por ejemplo: –  El día que menos niños se atendieron en consulta fue el miércoles. –  El día que más adultos se atendieron en consulta fue el martes. –  Del lunes al martes disminuyó el número de niños atendidos. Comente después algunas de ellas en común. Inteligencia espacial 20 16 12 8 4 0 Luis Jon María 56
UNIDAD 8 3 Haz una encuesta en clase y completa la tabla en tu cuaderno. Para cada día de la semana, pregunta cuántas personas han dormido muy bien, bien o regular, y apúntalo en la tabla. 4 Copia y completa el gráfico con los resultados de la encuesta. 5 Observa el gráfico que has construido y contesta. ¿Cuántos alumnos durmieron muy bien el lunes? ¿Cuántos durmieron regular el miércoles? ¿Qué día hubo más alumnos que durmieran bien? ¿Qué día es el que menos alumnos durmieron muy bien? ¿Cuál fue la respuesta más común el miércoles? ¿Cuál fue la menos común el martes? ¿Qué tipo de respuesta fue la más común en los cuatro días? Muy bien Bien Regular Lunes Martes Miércoles Jueves 5 ¡No olvides anotar tu voto! 8 Muy bien Bien Regular Númerodealumnos Lunes MiércolesMartes Jueves 18 16 14 12 10 8 6 4 2 0 127 ES0000000024590 663006-Unidad 08_22591.indd 127 10/03/2015 13:16:53 Notas Competencias •  Competencia digital. Comente con los alumnos que muchas informaciones se transmiten mediante gráficos y, por tanto, es muy importante saber interpretarlos y representarlos correctamente. Con la ayuda de programas informáticos, puede realizar (o pedir a los alumnos que lo hagan) distintos gráficos de barras de tres características para trabajar los contenidos vistos en la doble página. 57
Tiempo y dinero9 Contenidos de la unidad SABER MEDIDA • El reloj digital. • Unidades de tiempo. • Problemas con unidades de tiempo y dinero. SABER HACER MEDIDA • Lectura y escritura de horas en el reloj digital, reconociendo horas antes y después del mediodía. • Cálculo del tiempo transcurrido entre dos horas dadas. • Obtención y representación de la hora que es, dada la hora de inicio y el tiempo transcurrido. • Utilización de las equivalencias entre las distintas unidades de tiempo. • Resolución de problemas de tiempo. • Resolución de problemas donde aparezcan situaciones de compra. RESOLUCIÓN DE PROBLEMAS • Cambio de los datos de un problema para obtener una solución distinta. • Invención de un problema cambiando los datos para que se resuelva según unos cálculos dados.   TAREA FINAL • Programar horarios. SABER SER FORMACIÓN EN VALORES • Valoración de la utilidad de las unidades de tiempo y dinero. • Interés por la resolución de problemas cotidianos donde aparezcan unidades de tiempo y dinero. 58
BIBLIOTECA DEL PROFESORADO Programación didáctica de aula Recursos para la evaluación • Evaluación de contenidos. Unidad 9: pruebas de control B y A. • Evaluación por competencias. Prueba 9. •  Rúbrica. Unidad 9. Enseñanza individualizada • Plan de mejora. Unidad 9. • Programa de ampliación. Unidad 9. Proyectos de trabajo cooperativo • Proyecto del segundo trimestre. Recursos complementarios • Fichas para el desarrollo de la inteligencia. • Operaciones y problemas. Aprendizaje eficaz • Técnicas de estudio y presentación de exámenes. Proyectos interdisciplinares • Programa de Educación en valores. • Programa de Educación emocional. • Inteligencias múltiples. RECURSOS DIGITALES LibroMedia • Unidad 9: actividades y recursos. MATERIAL DE AULA Láminas OTROS MATERIALES DEL PROYECTO Cuaderno del alumno • Segundo trimestre. Unidad 9. Solución de problemas. Método DECA SUGERENCIA DE TEMPORALIZACIÓN Enero MarzoFebrero ES0000000024590 663006_Matematicas_4_GRAZ_24259 PRIMARIA PRIMARIA Matemáticas PRIMARIA ANDALUCÍAMatemáticas ANDALUCÍA Matemáticas ANDALUCÍA ES0000 000024 590 663006 _Matem aticas_4_GRA Z_2425 9.indd 1 04/03/2 015 11:21:19 ES0000000024593 663039_Cdno_Matematicas_4-2_22732 PRIMARIA Matemáticas Segundo trimestre Matemáticas Segundo trimestre PRIMARIA CUADERNO CUADERNO ES0000000024593 663039_Cdno_Matematicas_4-2_22732.indd 1 19/02/2015 16:56:18 59
9 Tiempo y dinero Visita a un parque eólico Hoy los alumnos de 4.º de Primaria visitarán un parque eólico. La profesora les muestra algunas fotos y les explica cómo funcionan esos enormes molinos de viento. Todos están impresionados de su tamaño. Después, la profesora reparte a cada uno el horario. –¿Podremos hacernos una foto con los molinos? –pregunta María. –¡Seguro que sí! –contesta la profesora. VISITA A UN PARQUE EÓLICO 9 : 00 Salida 9 : 45 Charla informativa 10 : 30 Visita al parque 14 : 15 Comida 16 : 00 Regreso 128 ES0000000024590 663006-Unidad 09_22592.indd 128 10/03/2015 13:22:44 VISITA A UN PARQUE EÓLICO 9 : 00 Salida 9 : 45 Charla informativa 10 : 30 Visita al parque 14 : 15 Comida 16 : 00 Regreso Propósitos •  Reconocer situaciones reales en las que se utilicen unidades de tiempo. •  Recordar los conceptos básicos necesarios para el desarrollo   de la unidad. Previsión de dificultades •  Algunos alumnos pueden tener dificultad en interpretar las horas, después del mediodía, en un reloj digital y representar estas horas   en un reloj de agujas. Si lo ve necesario, realice varias actividades de este tipo para subsanar estos posibles errores. •  Los alumnos pueden tener dificultad para elegir la operación adecuada (multiplicación o división) al resolver problemas con unidades de tiempo. Realice numerosas actividades   en uno y otro sentido. Trabajo colectivo sobre la lámina Haga que un alumno lea la situación planteada y pregunte a los alumnos si han visto alguna vez un parque eólico, dónde lo vieron, cómo son los molinos, etc. A continuación, pídales que realicen las actividades propuestas de forma individual   y corrija los resultados en la pizarra, despejando las dudas que hayan podido surgir. 1 Salida Comida Visita Charla 2 Pasan 45 minutos. 3 La visita comenzó a las 10   y media y terminó a las 12. 4 R. M. Se añade 1 hora y 30 minutos a la hora que comenzó   la visita que fue a las 10 y media. Otras formas de empezar •  Comente con los alumnos las horas más importantes del horario   del colegio: a qué hora entran, a qué hora es el recreo, a qué hora es   la comida, a qué hora se sale... Escríbalas en la pizarra y pregunte a los alumnos si creen que es necesario conocer la hora, por qué creen que lo es, etc. Explique la importancia en nuestra sociedad de tener una medida   de tiempo común para todos. 12 1 2 3 4 567 8 9 10 11 12 1 2 3 4 567 8 9 10 11 12 1 2 3 4 567 8 9 10 11 12 1 2 3 4 567 8 9 10 11 12 1 2 3 4 567 8 9 10 11 12 1 2 3 4 567 8 9 10 11 12 1 2 3 4 567 8 9 10 11 12 1 2 3 4 567 8 9 10 11 12 1 2 3 4 567 8 9 10 11 12 1 2 3 4 567 8 9 10 11 12 1 2 3 4 567 8 9 10 11 12 1 2 3 4 567 8 9 10 11 12 1 2 3 4 567 8 9 10 11 12 1 2 3 4 567 8 9 10 11 12 1 2 3 4 567 8 9 10 11 12 1 2 3 4 567 8 9 10 11 60
12 1 2 3 4 567 8 9 10 11 1 Copia el reloj en tu cuaderno y representa la hora a la que se realiza cada actividad. Salida … Comida … Visita a la estación … Charla informativa … 2 ¿Cuánto tiempo pasa desde la salida hasta que empieza la charla informativa? 3 La visita a la estación duró 1 hora y 30 minutos. ¿A qué hora terminó? 4 EXPRESIÓN ORAL. Explica cómo has calculado la hora a la que terminó la visita. Lee, comprende y razona La lectura de horas en relojes de agujas y digitales Son las 8 y cuarto de la mañana. Son las 4 y diez de la tarde. 1 Escribe la hora que marca cada reloj. La suma y la resta de decimales 1.º Coloca los números de forma que coincidan en columna las unidades del mismo orden. 2.º Suma o resta como si fueran números naturales y escribe la coma en el resultado debajo de las comas. 2 Coloca los números y calcula en tu cuaderno. 53,19 1 28,67 72,89 1 8,6 49,75 2 27,16 91,34 2 8,7 ¿Qué sabes ya? TAREA FINAL Programar horarios Al final de la unidad programarás los horarios de un gimnasio. Antes, estudiarás las horas, las unidades de tiempo y resolverás problemas. SABER HACER 12 1 2 3 4 567 8 9 10 11 12 1 2 3 4 567 8 9 10 11 12 1 2 3 4 567 8 9 10 11 12 1 2 3 4 567 8 9 10 11 12 1 2 3 4 567 8 9 10 11 14:1508:00 21:3021 :30 8 :00 8 :15 14 :15 16 :10 5 6, 3 9 1 9, 8 6 6, 1 9 7 3, 0 4 2 2 6, 5 7 4 6, 4 7 129 ES0000000024590 663006-Unidad 09_22592.indd 129 10/03/2015 13:22:46 UNIDAD 9 ¿Qué sabes ya? Recuerde con los alumnos la lectura y representación de las horas en relojes analógicos y digitales. Pídales que digan las características de cada uno. Trabaje también la suma y resta de decimales, necesarias para los cálculos con cantidades de dinero. 1 Las 10 y media. Las 5 y diez. Las 2 menos cuarto. Las 8 de la mañana. Las 2 y cuarto de la tarde. Las 9 y media de la noche. 2 •  53,19 1 28,67 5 81,86 •  72,89 1 8,6 5 81,49 •  49,75 2 27,16 5 22,59 •  91,34 2 8,7 5 82,64 Notas Competencias • Comunicación lingüística. Al realizar las actividades propuestas después de la lectura es importante comprobar que los alumnos conocen los términos matemáticos relativos al tiempo y los utilizan correctamente. Anímelos siempre a razonar sus respuestas de forma coherente. • Aprender a aprender. Comente con los alumnos la importancia que tiene asentar bien los conocimientos estudiados para poder avanzar con seguridad. Muestre que en esta unidad van a seguir aprendiendo sobre dos temas que ya conocían: el tiempo y el dinero. 61
El reloj digital 1 Escribe cómo se lee la hora de cada reloj digital como en un reloj de agujas. Piensa si la hora es antes o después del mediodía. 2 Representa en tu cuaderno la hora de cada reloj digital en un reloj de agujas. RECUERDA En un reloj digital, las horas después del mediodía se representan por 13, 14, 15... EJEMPLO La 1 y cinco de la tarde.13:05 17:10 15:40 17:45 20:35 21:50 22:55 13:05 5:10 15:20 10:35 20:40 23:45 17:10 EJEMPLO La ruta del autobús escolar comienza a las 8 de la mañana y termina a las 9. Observa cómo se expresan las horas de las 8 a las 9 en un reloj digital. 8:00 Las 8 8:05 Las 8 y cinco 8:10 Las 8 y diez 8:15 Las 8 y cuarto 8:20 Las 8 y veinte 8:25 Las 8 y veinticinco 8:30 Las 8 y media 8:35 Las 9 menos veinticinco 8:40 Las 9 menos veinte 8:45 Las 9 menos cuarto 8:50 Las 9 menos diez 8:55 Las 9 menos cinco 9:00 Las 9 12 1 2 3 4 567 8 9 10 11 12 1 2 3 4 567 8 9 10 11 12 1 2 3 4 567 8 9 10 11 130 ES0000000024590 663006-Unidad 09_22592.indd 130 10/03/2015 13:22:48 Propósitos •  Interpretar las horas antes   y después del mediodía en un reloj digital. •  Representar horas antes y después del mediodía en un reloj digital. •  Resolver problemas con tiempos. Sugerencias didácticas Para explicar. Lea la situación planteada en el cuadro informativo   y muestre a los alumnos cómo   se expresan las horas de las 8   a las 9 en un reloj digital. Comente   en especial los casos a partir   de «y media» ya que son los más nuevos para los alumnos. Señale   que, cuando el número de minutos   es mayor que 30, es necesario referirse a la hora siguiente. Muestre que, cuando la cifra de las horas es mayor de 12, nos estamos refiriendo a horas después del mediodía. Para reforzar. Diga una hora   (o escríbala en la pizarra) y pida   a varios alumnos que salgan   y dibujen en un reloj digital la hora   que sería un cuarto de hora, media hora, tres cuartos de hora, 1 hora,   1 hora y cuarto… antes o después. Actividades 1 •  La 1 y cinco de la tarde. •  Las 5 y diez de la mañana. •  Las 3 y veinte de la tarde. •  Las 11 menos veinticinco   de la mañana. •  Las 9 menos veinte de la tarde. •  Las 12 menos cuarto   de la noche. 2 Otras actividades •  Proponga a los alumnos construir un reloj digital con cartulina.   Para ello, indíqueles que hagan dos tiras largas de unos 2 cm de ancho   y que escriban en vertical en una tira las horas (0, 1, 2, …, 23)   y en la otra los minutos (00, 05, 10, …, 55). Además, harán un rectángulo de 10 3 5 cm, escribirán   en el centro el signo : y dibujarán dos ventanillas,   perforando las líneas horizontales para introducir   las tiras anteriores. •  Utilice este reloj como apoyo al realizar las actividades   de escritura y lectura de horas, cálculo de tiempos   transcurridos, etc. 10 11 12 13 14 15 20 25 30 35 17 18 19 45 50 55 15    :    40 12 1 2 3 4 567 8 9 10 11 12 1 2 3 4 567 8 9 10 11 12 1 2 3 4 567 8 9 10 11 12 1 2 3 4 567 8 9 10 11 12 1 2 3 4 567 8 9 10 11 12 1 2 3 4 567 8 9 10 11 62
14:1508:00 21:30 9 3 Calcula y escribe en tu cuaderno qué hora marcará cada reloj digital. 16:35 2 horas y 20 minutos después. 3 horas y media después. 20:45 3 horas y 20 minutos antes. 4 horas y media antes. Problemas 4 Resuelve. Hoy comienzan las fiestas del barrio y Carlota y sus amigos leen las actividades propuestas. ¿Qué actividades están propuestas por la mañana? ¿Y por la tarde? ¿Cuánto tiempo dura el guiñol? ¿Y los pintacaras? ¿Cuánto tiempo dura cada actividad programada por la tarde? Carlota quiere ir al guiñol y luego a los pintacaras. ¿Podrá ir y volver a su casa, que está a 10 minutos del lugar donde se hace el guiñol? Invéntate una actividad que se realice por la tarde y que dure 1 hora y media. Escribe a qué hora comienza y termina. Resta 11 a un número: primero resta 10 y luego resta 1 32 2 11 208 2 11 3.176 2 11 47 2 11 384 2 11 4.185 2 11 58 2 11 415 2 11 6.084 2 11 CÁLCULO MENTAL 147 137 136 2 10 2 1 2 11 HAZLO ASÍ 14:25 3 horas y 15 minutos después El reloj marcará: 17:40 3 horas después 14 1 3 5 17 15 minutos después 25 1 15 5 40 14:25 17:40 COMIENZA TERMINA Guiñol 10:30 11:45 Pintacaras 12:10 13:30 Payasos 17:15 19:30 Teatro 21:00 22:45 131 ES0000000024590 663006-Unidad 09_22592.indd 131 10/03/2015 13:22:49 UNIDAD 9 3   16:35 • • • • 4 • Por la mañana: guiñol y pintacaras. Por la tarde: payasos y teatro. • El guiñol dura 1 hora y 15 minutos. Los pintacaras duran 1 hora y 20 minutos. • Los payasos duran 2 horas y 15 minutos. El teatro dura 1 hora y 45 minutos. • Carlota tarda 20 minutos en ir y volver a su casa. Si sale del guiñol a las 11:45 más los 20 minutos que tarda en ir y volver, a las 12:05 ya estará, luego sí puede ir y volver a su casa. • R. M. Carrera ciclista: comienza a las 18:30 y termina a las 20:00. Cálculo mental •  21 •  197 •  3.165 •  36 •  373 •  4.174 •  47 •  404 •  6.073 Notas Otras actividades •  Pida a los alumnos que hagan el horario de un día de colegio, escribiendo cada hora en un reloj digital. En él deben reflejar, además de las horas a las que tienen cada clase o actividad extraescolar, las horas a las que suelen realizar otras actividades diarias como: levantarse, desayunar, salir de casa hacia el colegio, comer, merendar, hacer los deberes, jugar, ver la televisión, ducharse, acostarse, etc. Haga una puesta en común y plantee ejercicios de estimación y de cálculo de tiempos transcurridos: el tiempo que dura una actividad o el que pasa entre dos actividades dadas… 20:45 17:25 18:55 20:05 16:15 Inteligencia interpersonal 63
Unidades de tiempo 1 Calcula en tu cuaderno cuántos meses son. 2 trimestres 3 trimestres 4 trimestres 2 cuatrimestres 4 cuatrimestres 5 cuatrimestres 3 semestres 4 semestres 6 semestres 2 ¿Cuántos años son? Calcula en tu cuaderno. 2 lustros 3 lustros 5 lustros 3 décadas 5 décadas 7 décadas 3 siglos 4 siglos 6 siglos 3 Calcula. Recuerda que el año tiene 365 días y que un año tiene 12 meses. Para medir el tiempo utilizamos distintas unidades, unas menores que el año y otras mayores. MENORES QUE EL AÑO Un trimestre es 3 meses. Un cuatrimestre es 4 meses. Un semestre es 6 meses. MAYORES QUE EL AÑO Un lustro es 5 años. Una década es 10 años. Un siglo es 100 años. ¿Cuántos trimestres son? 9 meses 15 meses 12 meses 21 meses ¿Cuántos lustros son? 10 años 20 años 15 años 30 años ¿Cuántos cuatrimestres son? 12 meses 24 meses 16 meses 32 meses ¿Cuántas décadas son? 20 años 60 años 50 años 80 años ¿Cuántos semestres son? 18 meses 30 meses 24 meses 42 meses ¿Cuántos siglos son? 200 años 500 años 400 años 900 años 132 ES0000000024590 663006-Unidad 09_22592.indd 132 10/03/2015 13:22:54 Propósitos •  Conocer la equivalencia entre   las distintas unidades de tiempo. •  Resolver situaciones reales con unidades de tiempo. Sugerencias didácticas Para explicar. Pida a los alumnos   que observen el cuadro y recuérdeles los días y los meses que tiene un año. Exprese que hay unidades de tiempo menores que el año y nómbrelas escribiendo su equivalencia en la pizarra. Proceda de forma análoga con las unidades de tiempo mayores que el año. Para reforzar. Agrupe a los alumnos   y pídales que preparen, en forma   de mural, de línea del tiempo, de esquema, etc., un resumen donde aparezcan todas las unidades   de tiempo y sus equivalencias. Actividades 1 •  6 meses •  8 meses •  9 meses •  16 meses •  12 meses •  20 meses •  18 meses •  24 meses •  36 meses 2 •  10 años •  30 años •  15 años •  50 años •  25 años •  70 años • 300 años • 400 años •  600 años 3 •  3 trimestres •  2 lustros •  4 trimestres •  3 lustros •  5 trimestres •  4 lustros •  7 trimestres •  6 lustros •  3 cuatrimestres •  2 décadas •  4 cuatrimestres •  5 décadas •  6 cuatrimestres •  6 décadas •  8 cuatrimestres •  8 décadas •  3 semestres •  2 siglos •  4 semestres •  4 siglos •  5 semestres •  5 siglos •  7 semestres •  9 siglos Otras actividades •  Pregunte a los alumnos cuántos y cuáles son los meses del año y escríbalos ordenados en la pizarra. Calcule de forma colectiva cuántos trimestres   y semestres hay en un año, y qué meses forman cada uno de ellos. Hágales observar que el curso escolar no comienza en enero, por lo que el primer trimestre de curso no coincide con el primer trimestre del año. •  Nombre algunas fechas señaladas del año para que los alumnos digan   de qué trimestre o semestre son. Por ejemplo: el día de Reyes,   el comienzo de las vacaciones de verano o Navidad, el cumpleaños   de cada niño… 64
9 Lee y contesta. Mario le dice a su amiga Lorena: «Ayer, mi hermano pequeño tenía 8 años y el año que viene cumplirá 10». ¿Qué día cumple los años el hermano de Mario? Razona tu respuesta. RAZONAMIENTO 4 Lee y calcula. Nuria hizo un curso de fotografía durante un cuatrimestre. ¿Cuántos días duró el curso? Alfredo viaja a Sevilla cada 90 días. ¿Cada cuántos meses va a Sevilla? Problemas 5 Fíjate en el año en el que se inventó cada aparato y calcula. ¿Cuántos años hace que se inventó cada aparato? ¿Cuántos siglos y años son? ¿Cuántos siglos y años pasaron desde la invención de los prismáticos hasta la invención del teléfono? ¿Cuántas décadas y años son? ¿Cuántos años pasaron desde la invención del microscopio hasta la invención de los prismáticos? ¿Cuántos lustros y años son? 6 Resuelve. Fabiana compra una finca y la va a pagar en 10 años, pagando la misma cuota cada trimestre. ¿Cuántas cuotas pagará en un año? ¿Y en un lustro? ¿Cuántas cuotas pagará en total en los 10 años? En cada cuota Fabiana paga 545 €. ¿Cuánto pagará Fabiana por la finca? MICROSCOPIO Año 1590 PRISMÁTICOS Año 1608 PRESTA ATENCIÓN Los meses tienen 30 o 31 días, salvo febrero que tiene 28 o 29. Al hacer cálculos se consideran todos los meses de 30 días. TELÉFONO Año 1876 133 ES0000000024590 663006-Unidad 09_22592.indd 133 10/03/2015 13:22:57 UNIDAD 9 4 • 4 3 30 5 120 El curso duró 120 días. • 90 : 30 5 3 Cada 3 meses viaja a Sevilla. 5 • Teléfono Año actual 2 1876 Ejemplo: 2.016 2 1.876 5 140 años 5 5 1 siglo y 40 años Microscopio 2.016 2 1.590 5 426 años 5 5 4 siglos y 26 años Prismáticos 2.016 2 1.608 5 408 años 5 5 4 siglos y 8 años • 1.876 2 1.608 5 268 años 5 5 26 décadas y 8 años • 1.608 2 1.590 5 18 años 5 5 3 lustros y 3 años 6 • 12 : 3 5 4 5 3 4 5 20 Pagará 4 cuotas al año y 20 cuotas en un lustro. • 4 3 10 5 40 Pagará 40 cuotas en 10 años. • 40 3 545 5 21.800 Pagará 21.800 € por la finca. Razonamiento El hermano de Mario cumple los 9 años el 1 de enero. De esta forma, el día 31 de diciembre tenía 8 años y el 1 de enero del próximo año cumplirá 10 años. Notas Otras actividades • Copie en la pizarra la siguiente sopa de letras. Pida a nueve alumnos que rodeen cada uno una unidad de tiempo. Al final, pida a los alumnos que ordenen las nueve unidades de mayor a menor tiempo, que definan cada unidad relacionándola con otra y que inventen una oración con cada unidad. Por último, haga una puesta en común con las propuestas hechas. T R I M E S T R E A O S P I R E A O D Q L D A N O M E S I E B E H U D E A T O H U C I T O S I G L O S A Ñ O L T N E A R I D F R A R O D I A E A L S I E P M O T 65
Problemas con unidades de tiempo y dinero 1 ¿Cuánto dinero hay? Exprésalo con un número decimal. 2 Escribe el menor número posible de monedas y billetes para expresar cada precio. RECUERDA Hay monedas de 1, 2, 5, 10, 20 y 50 céntimos y de 1 € y 2 €. Hay billetes de 5, 10, 20, 50, 100, 200 y 500 €. EJEMPLO 18,35 Billetes: 1 de 10 € y 1 de 5 €. Monedas: 1 de 2 €, 1 de 1 €… 18,35 € 130,84 € 21,75 € 265,90 € Alejandra quiere comprar un conjunto de muebles para el jardín cuyo precio es de 879,99 €. En su cartera lleva estos billetes y monedas. ¿Cuánto dinero le sobra? Billetes 500 1 200 1 100 1 50 1 20 1 10 1 5 5 885 € Monedas 50 1 20 5 70 céntimos 5 0,70 € Dinero que tiene Dinero que le sobra 8 8 5 1 0, 7 0 8 8 5, 7 0 8 8 5, 7 0 2 8 7 9, 9 9 0 0 5, 7 1 A Alejandra le sobran 5,71 €. 134 ES0000000024590 663006-Unidad 09_22592.indd 134 10/03/2015 13:23:08 Propósitos •  Resolver situaciones reales   con unidades de tiempo y dinero. Sugerencias didácticas Para explicar. Haga que los alumnos lean la situación planteada y observen las monedas y billetes. Recuerde   con ellos todos los billetes y monedas de nuestro sistema monetario. Comente la forma de expresar cantidades de dinero usando   los números decimales y razone   qué operaciones hay que realizar para resolver el problema. Señale a los alumnos que aparte   de operar con decimales a la hora   de calcular pueden también expresar todas las cantidades en céntimos   y operar con los números naturales obtenidos. Para reforzar. Trabaje situaciones de compra reales propuestas por usted o por los propios alumnos. Puede también realizar un pequeño mercadillo en el que los alumnos vendan y compren distintos objetos. Actividades 1 •  3,60 €      •  5,35 €      •  10,65 € 2 •  18,35 €: 1 billete de 10 €,   1 de 5 €, 1 moneda de 2 €,   1 de 1 €, 1 de 0,20 €,   1 de 0,10 € y 1 de 0,05 €. •  21,75 €: 1 billete de 20 €,   1 moneda de 1 €, 1 de 0,50 €, 1 de 0,20 € y 1 de 0,05 €. •  130,84 €: 1 billete de 100 €,   1 de 20 €, 1 de 10 €,   1 moneda de 0,50 €,   1 de 0,20 €, 1 de 0,10 €   y 2 de 0,02 €. •  265,90 €:1 billete de 200 €,  1 de 50 €, 1 de 10 €, 1 de 5 €, 1 moneda de 0,50 €   y 2 de 0,20 €. Otras actividades •  Trabaje de forma colectiva y oral, o de manera manipulativa, el cálculo (mental) de devoluciones de dinero con los siguientes grados de dificultad creciente: –  Hay que pagar una cantidad de céntimos y entregas 1 €. –  Hay que pagar una cantidad de céntimos y entregas 2 € o 5 €. –  Hay que pagar una cantidad de euros y céntimos y entregas el menor número de euros posible (te devuelven solo céntimos). –  Hay que pagar una cantidad de euros y céntimos y entregas el menor billete posible (te devuelven euros y céntimos) 66
3 Fíjate en las unidades de los datos y resuelve en tu cuaderno. Irene compra un rotulador y entrega para pagar un billete de 5 €. ¿Cuánto dinero le devuelven? Expresa en céntimos y resuelve: 5 € 5 500 céntimos 500 2 85 5 … céntimos le devuelven. Expresa en euros y resuelve: 85 céntimos 5 0,85 € 5 2 0,85 5 … € le devuelven. Pablo compra un sacapuntas y un cuaderno. – ¿Cuánto se gasta en total? – ¿Cuánto le devolverán si entrega para pagar 4 €? 4 Lee y resuelve. Elena se ha apuntado a natación tres días a la semana. En la tabla aparecen los minutos que estuvo nadando cada día. ¿Cuántos minutos en total nadó Elena esta semana? ¿Cuántas horas y minutos son? La semana pasada Elena nadó durante 165 minutos. ¿Cuánto pagó en total por las clases si 45 minutos cuestan 9 €? 9 3 Fíjate en las unidades de los datos y resuelve en tu cuaderno. Irene compra un rotulador y entrega para pagar un billete de 5 €. ¿Cuánto dinero le devuelven? Expresa en céntimos y resuelve: 5 € 5 500 céntimos 500 2 85 5 … céntimos le devuelven. Expresa en euros y resuelve: 85 céntimos 5 0,85 € 5 2 0,85 5 … € le devuelven. Pablo compra un sacapuntas y un cuaderno. – ¿Cuánto se gasta en total? – ¿Cuánto le devolverán si entrega para pagar 4 €? 4 Lee y resuelve. Elena se ha apuntado a natación tres días a la semana. En la tabla aparecen los minutos que estuvo nadando cada día. ¿Cuántos minutos en total nadó Elena esta semana? ¿Cuántas horas y minutos son? La semana pasada Elena nadó durante 165 minutos. ¿Cuánto pagó en total por las clases si 45 minutos cuestan 9 €? Resta 9 a un número: primero resta 10 y luego suma 1 26 2 9 194 2 9 2.823 2 9 49 2 9 275 2 9 5.414 2 9 67 2 9 578 2 9 7.121 2 9 80 2 9 740 2 9 9.150 2 9 CÁLCULO MENTAL 147 137 138 2 10 1 1 2 9 PRESTA ATENCIÓN Expresa siempre todos los datos en la misma unidad: euros o céntimos. Día Tiempo en minutos Lunes 35 Miércoles 30 Viernes 20 Sacapuntas 65 céntimos Cuaderno 2,45 € Rotulador 85 céntimos 135 ES0000000024590 663006-Unidad 09_22592.indd 135 10/03/2015 13:23:09 UNIDAD 9 3 • 500 2 85 5 415 5 2 0,85 5 4,15 Le devuelven 415 cts. 5 5 4,15 €. •  65 1 245 5 310 cts. 0,65 1 2,45 5 3,10 € Gasta 310 cts. 5 3,10 €. 400 2 310 5 90 cts. 4 2 3,10 5 0,90 € Le devuelven 90 cts. 5 0,90 €. 4 • 35 1 30 1 20 5 85 minutos 5 5 1 hora y 25 minutos Esta semana, Elena nadó 1 hora y 25 minutos. • 165 : 45 c 5 3, r 5 30 La semana pasada, Elena estuvo nadando 3 días durante 45 minutos y otro día 30 minutos, luego pagará: 4 3 9 5 36 €. Cálculo mental •  17 •  185 •  2.814 •  40 •  266 •  5.405 •  58 •  569 •  7.112 •  71 •  731 •  9.141 Notas Competencias •  Competencia social y cívica. La situación de la actividad 4 permite, de manera sencilla, suscitar un debate en clase sobre diferentes aspectos relacionados con esta competencia. Puede comentar con ellos la importancia de la actividad física para nuestra salud, el empleo del tiempo libre de forma constructiva, la necesidad de aprovechar las clases al máximo, el ejercicio de nuestros derechos y deberes como consumidores… 67
Resuelve cada problema y después cambia dos datos para obtener otra solución. 1 En la furgoneta de Gonzalo se puede cargar un máximo de 1.000 kilos. Gonzalo tiene que cargar un paquete de 275 kilos, otro de 450 kilos y el tercero de 300 kilos. ¿Podrá cargar los tres paquetes juntos en su furgoneta? 2 Laura va a hacer un mural pegando postales de paisajes. Laura necesita 18 postales y ha comprado 5 sobres con 3 postales cada uno. ¿Tendrá Laura suficientes postales para hacer el mural? 3 Javier tiene en su huerto 5 filas de manzanos con 12 manzanos cada uno y 7 filas de perales con 15 perales cada uno. ¿Tiene Javier en su huerto más de 200 árboles frutales? 4 En el restaurante de Paula hay 15 mesas. Paula tiene 100 flores y quiere poner en cada mesa un jarrón con 15 flores. ¿Tendrá suficientes flores para todas las mesas? Vamos a leer el problema y cambiar dos datos para obtener otra solución. Los alumnos de 3.º y 4.º han preparado una función de teatro y la van a representar en un colegio cercano. Van 29 alumnos de 3.º, 38 de 4.º y 6 monitores. Para el traslado, han alquilado un autocar de 70 plazas. ¿Podrán ir todos juntos en el autocar? Si sumamos los que van, necesitan: 29 1 38 1 6 5 73 plazas, luego no pueden ir todos en el autocar. Para obtener otra solución, es decir, conseguir que todos vayan en el autocar, la suma de los tres datos ha de ser menor o igual que 70. Como tenemos que cambiar dos datos del problema, un posible problema sería: Los alumnos de 3.º y 4.º han preparado una función de teatro y la van a representar en un colegio cercano. Van 27 alumnos de 3.º, 36 de 4.º y 6 monitores. Para el traslado, han alquilado un autocar de 70 plazas. ¿Podrán ir todos juntos en el autocar? Comprueba que este problema tiene otra solución. Cambiar datos para obtener una solución distinta Solución de problemas 136 ES0000000024590 663006-Unidad 09_22592.indd 136 10/03/2015 13:23:11 Propósitos •  Cambiar los datos de un problema para obtener otra solución. Sugerencias didácticas Para explicar. Haga que los alumnos lean el problema propuesto y comente que para que la solución sea distinta tenemos que conseguir que puedan   ir todos en el autocar. Muestre que existen muchos posibles cambios   y que en el ejemplo resuelto aparece uno solo de ellos. Pídales que aporten algunos más. Señale la necesidad   de comprobar que el nuevo problema que generan tiene una solución diferente. Actividades 1 275 1 450 1 300 5 1.025  No podrá cargarlos.  R. M. Gonzalo tiene que cargar   un paquete de 275 kg, otro   de 450 kg y el tercero de 200 kg. 2 5 3 3 5 15  No tendrá suficientes postales.  R. M. Laura necesita 18 postales   y ha comprado 5 sobres   de 4 postales cada uno. 3 5 3 12 1 7 3 15 5 165  Tiene menos de 200 frutales.  R. M. Javier tiene en su huerto   9 filas de manzanos con 15 manzanos cada uno y 7 filas de perales con 20 perales cada uno. 4 15 3 15 5 225  No tiene flores suficientes.  R. M. En el restaurante de Paula hay 15 mesas. Paula tiene   260 flores y quiere poner en cada mesa 15 flores. 5 45 cm 1 65 cm 1 70 cm 5 5 180 cm  No tiene suficiente cinta.  R. M. Lucía tiene 165 cm de roja, 96 cm de verde y 125 cm   de amarilla. 6 2 3 6 1 3 3 12 5 48  No podrá hacer las rosquillas.  R. M. Alberto tiene 8 cartones   de 10 huevos cada uno   y 4 cartones de 12 huevos. Otras actividades •  Proponga a los alumnos problemas similares a los propuestos   en esta página para que resuelvan de forma individual en sus cuadernos.   Una vez resueltos haga que varios alumnos expongan al resto de la clase   su problema y realice una puesta en común con las diversas propuestas.  Por ejemplo:   Luis puede almacenar en su granja un total de 1.000 kg de pienso.   Hoy le han traído 25 sacos de 15 kg cada uno, 15 sacos de 20 kg cada uno  y 15 sacos de 30 kg cada uno. ¿Podrá almacenar en su granja todo   el pienso? 68
Cambia los datos marcados en rojo para que la solución del problema sea la que se indica. Después, escribe el nuevo problema en tu cuaderno. 1 Un pabellón de baloncesto tiene capacidad para 1.500 personas. El primer día que se pusieron en venta las entradas, se vendieron 489, el segundo día, 525, y el tercer día, 350. ¿Cuántas entradas quedaron por vender? 2 Miguel tiene en su frutería 4 cajas de manzanas rojas de 13 kilos cada una y 3 cajas de manzanas verdes de 17 kilos cada una. Ha tenido que tirar 15 kilos de manzanas por estar estropeadas. ¿Cuántos kilos de manzanas le quedan a Miguel? 3 Adela reparte en partes iguales 20 gafas rojas, 14 azules y 18 grises en partes iguales entre 2 expositores. ¿Cuántas gafas coloca en cada expositor? 9 Resuelve cada problema. Después, cambia el valor de tres o más datos para obtener otra solución y escribe el nuevo problema. 5 Para hacer un trabajo manual, Lucía necesita 3 m de cinta. Tiene 45 cm de cinta roja, 65 cm de cinta verde, 70 cm de cinta azul y 25 cm de cinta amarilla. ¿Tendrá suficiente cinta? Recuerda que 1 m 5 100 cm. 6 Hoy, Alberto va a hacer rosquillas en su pastelería. En la receta ve que necesita 52 huevos. Alberto tiene 2 cartones de 6 huevos cada uno y 3 cartones de 12 huevos cada uno. ¿Podrá Alberto hacer las rosquillas? 7 En las rebajas, Sofía compró 4 camisetas a 15 € cada una, 3 camisas a 19 € cada una y 2 cinturones a 10 € cada uno. ¿Tuvo suficiente para pagar con 100 €? 8 Para celebrar su cumpleaños, Sandra compra una bolsa con 15 globos rojos, una con 35 globos azules, una con 20 globos verdes y otra con 10 globos amarillos. El total de globos lo reparte en partes iguales entre 5 mesas. ¿Podrá poner 16 globos en cada mesa? 9 Luisa pesa 20 kg, Antonio 23 kg, Sara 4 kg más que Antonio y Silvia 2 kg menos que Luisa. ¿Pesan más de 110 kg todos juntos? INVENTA TUS PROBLEMAS Cambia los datos marcados en rojo para que la solución del problema sea la que se indica. Después, escribe el nuevo problema en tu cuaderno. 1 Un pabellón de baloncesto tiene capacidad para 1.500 personas. El primer día que se pusieron en venta las entradas, se vendieron 489, el segundo día, 525, y el tercer día, 350. ¿Cuántas entradas quedaron por vender? 2 Miguel tiene en su frutería 4 cajas de manzanas rojas de 13 kilos cada una y 3 cajas de manzanas verdes de 17 kilos cada una. Ha tenido que tirar 15 kilos de manzanas por estar estropeadas. ¿Cuántos kilos de manzanas le quedan a Miguel? 3 Adela reparte en partes iguales 20 gafas rojas, 14 azules y 18 grises en partes iguales entre 2 expositores. ¿Cuántas gafas coloca en cada expositor? 10 1 6 1 12 5 28 28 : 2 5 14 15 3 4 5 60 18 3 3 5 54 60 1 54 2 11 5 103 598 1 425 1 390 5 1.413 1.500 2 1.413 5 87 137 ES0000000024590 663006-Unidad 09_22592.indd 137 10/03/2015 13:23:12 UNIDAD 9 7 4 3 15 1 3 3 19 1 2 3 10 5 137 No tuvo suficiente. R. M. Sofía compra 2 camisetas a 15 € cada una, 2 camisetas a 19 € cada una y 2 cinturones a 8 € cada uno. 8 15 1 35 1 20 1 10 5 80 80 : 5 5 16 Sí podrá poner 16 globos. R. M. Sandra compra 10 globos rojos, 20 azules, 15 verdes y 8 amarillos. 9 20 1 23 1 27 1 18 5 88 Pesan menos de 110 kg. R. M. Luisa pesa 30 kg, Antonio 45 kg, Sara 9 kg más que Antonio y Silvia 1 kg menos que Luisa. Inventa tus problemas 1 R. M. El primer día se vendieron 598, el segundo día, 425 y el tercer día, 390. 2 R. M. Miguel tiene en su frutería 4 cajas de manzanas rojas de 15 kg cada una y 3 cajas de manzanas verdes de 18 kg cada una. Ha tenido que tirar 11 kg de manzanas por estar estropeadas. 3 R. M. Adela reparte en partes iguales 10 gafas rojas, 6 azules y 12 grises en partes iguales entre 2 expositores. Notas Competencias •  Iniciativa y emprendimiento. La autonomía a la hora de resolver los problemas y el emprendimiento necesario para tomar decisiones sobre la resolución y el proceso a seguir se practican intensivamente en las actividades de invención de problemas. Señale a los alumnos que es muy importante reflexionar sobre los datos que se van a cambiar teniendo en cuenta la solución dada y muestre la importancia de comprobar que el nuevo problema generado se resuelve con esos cálculos. Inteligencia interpersonal 69
6 Completa los relojes en tu cuaderno. Suma media hora cada vez. 19:35 ... hasta 21:35 Resta un cuarto de hora cada vez. 20:40 ... hasta 19:25 7 Calcula. ¿Cuántos meses son? 4 trimestres 5 trimestres 3 cuatrimestres 6 cuatrimestres 2 semestres 4 semestres ¿Cuántos años son? 2 lustros 4 lustros 3 décadas 5 décadas 4 siglos 6 siglos 8 Expresa en la unidad que se indica. 93 meses en trimestres. 84 meses en cuatrimestres. 120 meses en semestres. 50 años en lustros. 90 años en décadas. 800 años en siglos. 9 Piensa y escribe. María lleva en la mano tres monedas distintas, todas de un valor mayor que 10 céntimos. Expresa con un número decimal el dinero que puede llevar en la mano. 1 VOCABULARIO. Explica mediante un ejemplo cómo se leen en un reloj digital las horas antes y después del mediodía. 2 Representa en un reloj digital una hora antes del mediodía y otra hora después del mediodía. 3 Representa en un reloj de agujas la hora que marca cada reloj digital. 4 Lee la hora a la que se levantó y se acostó cada niño, y representa cada hora en un reloj digital. 5 ¿Qué hora marcará cada reloj digital? Calcula y completa en tu cuaderno. 2 horas y 30 minutos después 3 horas y 45 minutos después 4 horas y 50 minutos después 2 horas y 15 minutos antes 3 horas y 30 minutos antes 4 horas y 40 minutos antes ACTIVIDADES 21:25 8:15 Me levanté a las 9 y 10 de la mañana y me acosté a las 10 y media de la noche. LUIS ANA Me levanté a las 10 menos 20 de la mañana y me acosté a las 11 menos 10 de la noche. 10:20 2:40 9:35 19:10 22:15 16:45 138 ES0000000024590 663006-Unidad 09_22592.indd 138 10/03/2015 13:23:13 Propósitos •  Repasar los contenidos básicos   de la unidad. Actividades 1 R. L. 2 R. M. Antes del mediodía F 3:25  Después del mediodía F 14:45 3 4 LUIS ANA 5 • •  •  •  • •  6 19:35 F 20:05 F 20:35 F 21:05 F  21:35 F 20:40 F 20:25 F 20:10 F 19:55 F 19:40 F 19:25 7 •  12 meses •  15 meses •  12 meses •  24 meses •  12 meses •  24 meses •  10 años •  20 años •  30 años •  50 años •  400 años •  600 años 8 •  31 trimestres •  21 cuatrimestres •  20 semestres •  10 lustros •  9 décadas •  8 siglos Otras actividades •  Lleve a clase periódicos, forme varios grupos de alumnos y entregue   a cada grupo un periódico para que busquen en él la programación   de televisión. Pregunte a cada grupo a qué hora comienza y termina   un determinado programa (comente que consideren que un programa termina cuando comienza el siguiente, sin tener en cuenta el tiempo   de publicidad) y calcule de forma colectiva en la pizarra la duración de cada uno. A continuación, indique a cada niño que elija un programa   y calcule la duración del mismo. Después, lo dirá a sus compañeros   del grupo y entre todos comprobarán que es correcto. 10:45 13:05 17:55 12:00 19:10 16:45 9:10 9:40 22:30 22:50 12 1 2 3 4 567 8 9 10 11 12 1 2 3 4 567 8 9 10 11 12 1 2 3 4 567 8 9 10 11 12 1 2 3 4 567 8 9 10 11 12 1 2 3 4 567 8 9 10 11 12 1 2 3 4 567 8 9 10 11 70
12 Resuelve. Guillermo y Micaela consultan las actividades propuestas para este sábado en el club de campo. ¿A qué hora termina la actividad de senderismo? Representa en un reloj digital la hora a la que comienza y termina esta actividad. Guillermo dio un paseo a caballo. El paseo comenzó a las 4 menos cuarto de la tarde. ¿A qué hora terminó? Representa estas horas en un reloj digital. ¿Cuánto tiempo dura la visita a la cueva? Problemas 10 Lee y resuelve. El sábado Ricardo se levantó a las 10 y 20 de la mañana y salió a correr 2 horas y media después. ¿A qué hora salió a correr Ricardo? Irene cogió un autobús a las 5 y media de la tarde. Después de estar circulando 2 horas y cuarto, pararon media hora para tomar un refresco y llegaron a su destino a las 11 y cuarto de la noche. ¿Cuánto tiempo pasó desde que salió el autobús del descanso hasta llegar a su destino? 11 Resuelve. En el pueblo de Jorge se celebra un mercadillo medieval desde hace 80 años. ¿Cuántos años faltan para que el mercadillo cumpla un siglo? ¿Cuántas décadas de antigüedad tiene el mercadillo? 12 Resuelve. Guillermo y Micaela consultan las actividades propuestas para este sábado en el club de campo. ¿A qué hora termina la actividad de senderismo? Representa en un reloj digital la hora a la que comienza y termina esta actividad. Guillermo dio un paseo a caballo. El paseo comenzó a las 4 menos cuarto de la tarde. ¿A qué hora terminó? Representa estas horas en un reloj digital. ¿Cuánto tiempo dura la visita a la cueva? 9 13 Rosana ha cambiado en el banco una moneda de 2 € en monedas del mismo valor. Le han dado más de 20 monedas y menos de 100. ¿Por qué clase de moneda ha cambiado Rosana los 2 €? Demuestra tu talento Senderismo Hora de salida: 8 y media de la mañana. Duración: 3 horas y media. Paseo a caballo Desde las 9 de la mañana hasta las 5 de la tarde. Duración del paseo: 45 minutos. Visita a la cueva Hora de salida: 4 y cuarto de la tarde. Hora de regreso: 8 menos cuarto de la tarde. 139 ES0000000024590 663006-Unidad 09_22592.indd 139 10/03/2015 13:23:15 UNIDAD 9 9 0,20 1 0,50 1 1 5 1,70 0,20 1 0,50 1 2 5 2,70 0,50 1 1 1 2 5 3,50 Puede llevar 1,70 €, 2,70 € o 3,50 €. 10 • Salió a correr a las 12:50 o la 1 menos diez de la tarde. • 17:30 1 2 h 15 min 1 30 min 5 5 20:15 Hasta las 23:15 pasaron 3 horas. 11 • 1 siglo 5 100 años 100 2 80 5 20 Faltan 20 años. • 80 : 10 5 8 Tiene 8 décadas. 12 • 8:30 1 3 h 30 min 5 12:00 Termina a las 12 del mediodía. • Comenzó Terminó • Salida: 16:15 Regreso: 19:45 La visita a la cueva dura 3 horas y 30 minutos. Demuestra tu talento 13 2 € 5 200 céntimos 1 céntimo 200 monedas 2 céntimos 100 monedas 5 céntimos 40 monedas 10 céntimos 20 monedas 20 céntimos 10 monedas 50 céntimos 4 monedas Como le han dado más de 20 monedas y menos de 100, ha cambiado los 2 € por monedas de 5 céntimos y le han dado 40 monedas. Notas Competencias •  Competencia social y cívica. Plantee un debate en clase en el que aborde distintos temas relacionados con esta competencia y con el contexto que aparece en la actividad 12. Puede tratar asuntos como la importancia del deporte, el aprovechamiento sano del tiempo libre, el respeto a la naturaleza, la necesidad de la puntualidad en actividades sociales con otras personas… Pida a los alumnos que aporten sus ideas y opiniones. 8:30 15:45 12:00 16:30 Inteligencia naturalista 71
Programar horarios Lorena trabaja en un gimnasio y prepara los horarios de las nuevas actividades propuestas para este año. 1 Fíjate en el horario del gimnasio y representa cada hora en un reloj de agujas. 2 Busca y representa en un reloj de agujas. La hora que hay pilates los lunes. La hora que hay aeróbic los miércoles. La hora de natación de los jueves. La hora de yoga del sábado. 3 Lee y contesta. Javier ha ido a apuntarse a natación y estas son las ofertas que le han ofrecido. Averigua cuál es la mejor opción si quiere ir: 40 días 60 días 3 meses 4 TRABAJO COOPERATIVO. Programa con tu compañero. Realizad un horario para el lunes por la tarde. Inventad las actividades que habría y la hora de comienzo y de finalización de cada una. SABER HACER EJEMPLO DE LUNES A VIERNES: Abierto de a 12 1 2 3 4 567 8 9 10 11 12 1 2 3 4 567 8 9 10 11 Abono mensual 48 € Abono trimestral 120 € Sesión de 1 día 1 € LUNES MIÉRCOLES VIERNES 8:10 Pilates Bicicleta Yoga 10:15 Bicicleta Aeróbic Pilates MARTES JUEVES SÁBADO 17:45 Pilates Bicicleta Yoga 19:50 Bicicleta Natación Pilates Gimnasio Salud HORARIO DE APERTURA LUNES A VIERNES: de 8:00 a 22:30. SÁBADOS: de 9:15 a 21:45. DOMINGOS: de 8:10 a 15:00. 140 ES0000000024590 663006-Unidad 09_22592.indd 140 10/03/2015 13:23:18 Propósitos •  Desarrollar la competencia matemática resolviendo problemas reales. •  Repasar contenidos básicos. Actividades pág. 140 1   De lunes a viernes: De                      a Sábado: De                      a Domingo: De                      a 2 •  Pilates •  Aeróbic •  Natación •  Yoga 3 •  40 días: sesión 1 día F 40 € •  60 días: sesión 1 día F 60 € •  3 meses: sesión 1 día F 90 € 4 R. L. Actividades pág. 141 1 •  Trescientos seis mil ochocientos noventa. •  Setecientos ochenta mil setenta y tres. •  Novecientos veinticinco mil trescientos seis. •  Dos millones novecientos ochenta mil noventa. •  Seis millones setenta y seis mil trescientos seis. •  Nueve millones doscientos ocho mil treinta y siete. Desarrollo de la competencia matemática •  En esta página, los alumnos aplican lo aprendido en la unidad   para resolver una situación real de horarios de diversas actividades   de un gimnasio. De esta manera, potencian su competencia matemática.  A la hora de plantear el trabajo cooperativo, pida a los alumnos que sean creativos a la hora de plantear y exponer los horarios de las actividades.   Puede pedirles también que varíen los precios de los abonos mensual  y trimestral de la actividad 3 y que averigüen para qué períodos de tiempo sería mejor cada uno. 12 1 2 3 4 567 8 9 10 11 12 1 2 3 4 567 8 9 10 11 12 1 2 3 4 567 8 9 10 11 12 1 2 3 4 567 8 9 10 11 12 1 2 3 4 567 8 9 10 11 12 1 2 3 4 567 8 9 10 11 12 1 2 3 4 567 8 9 10 11 12 1 2 3 4 567 8 9 10 11 12 1 2 3 4 567 8 9 10 11 12 1 2 3 4 567 8 9 10 11 12 1 2 3 4 567 8 9 10 11 12 1 2 3 4 567 8 9 10 11 12 1 2 3 4 567 8 9 10 11 12 1 2 3 4 567 8 9 10 11 12 1 2 3 4 567 8 9 10 11 12 1 2 3 4 567 8 9 10 11 12 1 2 3 4 567 8 9 10 11 12 1 2 3 4 567 8 9 10 11 12 1 2 3 4 567 8 9 10 11 12 1 2 3 4 567 8 9 10 11 12 1 2 3 4 567 8 9 10 11 12 1 2 3 4 567 8 9 10 11 12 1 2 3 4 567 8 9 10 11 12 1 2 3 4 567 8 9 10 11 12 1 2 3 4 567 8 9 10 11 12 1 2 3 4 567 8 9 10 11 12 1 2 3 4 567 8 9 10 11 12 1 2 3 4 567 8 9 10 11 12 1 2 3 4 567 8 9 10 11 12 1 2 3 4 567 8 9 10 11 12 1 2 3 4 567 8 9 10 11 12 1 2 3 4 567 8 9 10 11 12 1 2 3 4 567 8 9 10 11 12 1 2 3 4 567 8 9 10 11 12 1 2 3 4 567 8 9 10 11 12 1 2 3 4 567 8 9 10 11 12 1 2 3 4 567 8 9 10 11 12 1 2 3 4 567 8 9 10 11 12 1 2 3 4 567 8 9 10 11 12 1 2 3 4 567 8 9 10 11 12 1 2 3 4 567 8 9 10 11 12 1 2 3 4 567 8 9 10 11 12 1 2 3 4 567 8 9 10 11 12 1 2 3 4 567 8 9 10 11 12 1 2 3 4 567 8 9 10 11 12 1 2 3 4 567 8 9 10 11 12 1 2 3 4 567 8 9 10 11 12 1 2 3 4 567 8 9 10 11 12 1 2 3 4 567 8 9 10 11 12 1 2 3 4 567 8 9 10 11 12 1 2 3 4 567 8 9 10 11 12 1 2 3 4 567 8 9 10 11 12 1 2 3 4 567 8 9 10 11 12 1 2 3 4 567 8 9 10 11 12 1 2 3 4 567 8 9 10 11 12 1 2 3 4 567 8 9 10 11 12 1 2 3 4 567 8 9 10 11 12 1 2 3 4 567 8 9 10 11 12 1 2 3 4 567 8 9 10 11 12 1 2 3 4 567 8 9 10 11 12 1 2 3 4 567 8 9 10 11 12 1 2 3 4 567 8 9 10 11 12 1 2 3 4 567 8 9 10 11 12 1 2 3 4 567 8 9 10 11 12 1 2 3 4 567 8 9 10 11 12 1 2 3 4 567 8 9 10 11 12 1 2 3 4 567 8 9 10 11 12 1 2 3 4 567 8 9 10 11 12 1 2 3 4 567 8 9 10 11 12 1 2 3 4 567 8 9 10 11 12 1 2 3 4 567 8 9 10 11 12 1 2 3 4 567 8 9 10 11 12 1 2 3 4 567 8 9 10 11 12 1 2 3 4 567 8 9 10 11 12 1 2 3 4 567 8 9 10 11 12 1 2 3 4 567 8 9 10 11 12 1 2 3 4 567 8 9 10 11 12 1 2 3 4 567 8 9 10 11 12 1 2 3 4 567 8 9 10 11 12 1 2 3 4 567 8 9 10 11 12 1 2 3 4 567 8 9 10 11 12 1 2 3 4 567 8 9 10 11 12 1 2 3 4 567 8 9 10 11 12 1 2 3 4 567 8 9 10 11 12 1 2 3 4 567 8 9 10 11 12 1 2 3 4 567 8 9 10 11 12 1 2 3 4 567 8 9 10 11 12 1 2 3 4 567 8 9 10 11 12 1 2 3 4 567 8 9 10 11 12 1 2 3 4 567 8 9 10 11 12 1 2 3 4 567 8 9 10 11 12 1 2 3 4 567 8 9 10 11 12 1 2 3 4 567 8 9 10 11 12 1 2 3 4 567 8 9 10 11 12 1 2 3 4 567 8 9 10 11 12 1 2 3 4 567 8 9 10 11 12 1 2 3 4 567 8 9 10 11 12 1 2 3 4 567 8 9 10 11 12 1 2 3 4 567 8 9 10 11 12 1 2 3 4 567 8 9 10 11 72
4 Escribe cómo se lee cada fracción y contesta. 2 3 3 5 6 8 7 9 ¿Qué fracción tiene el numerador mayor? ¿Qué fracción tiene el denominador menor? 5 Copia y rodea en cada caso la fracción que se indica. La fracción mayor 1 5 y 2 5 3 7 y 2 7 7 9 y 4 9 La fracción menor 3 7 y 3 5 6 8 y 6 9 7 10 y 7 9 1 Escribe cómo se lee cada número. 306.890 2.980.090 780.073 6.076.306 925.306 9.208.037 2 Calcula el cociente y el resto de estas divisiones y haz la prueba. 149 ; 7 8.023 ; 27 492 ; 27 24.528 ; 24 6.242 ; 15 75.852 ; 34 3 Calcula. 8 1 7 2 9 2 3 (9 2 3) 2 2 1 4 9 2 5 1 8 2 2 12 2 (6 – 4) 1 7 6 3 4 2 3 2 5 (4 1 2) 3 2 2 5 10 2 2 3 3 1 9 3 3 (11 2 7) 2 8 6 Para el comedor del colegio, han traído 75 yogures de fresa, 65 de limón y 32 naturales. Hoy se han comido 20 de fresa, 15 de limón y 9 naturales. ¿Cuántos yogures han quedado? 7 Guillermo va a poner baldosas en una habitación y calcula que necesita un total de 180 baldosas. Guillermo ha comprado 3 cajas con 75 baldosas cada una. ¿Le sobran o le faltan baldosas? ¿Cuántas? 8 Enrique salió de casa con 120 €. Se gastó un tercio del dinero en la pescadería y 35 € en la frutería. ¿Cuánto dinero le quedó? 9 En un colegio hay 450 alumnos. Un quinto de los alumnos van a actividades extraescolares. ¿Cuántos alumnos no van a actividades extraescolares? 10 Patricia trabaja en un supermercado. Hoy tiene que colocar 48 zumos de naranja y 72 de limón en partes iguales entre 4 estanterías. ¿Cuántos zumos pondrá en cada una? 11 Juan ha comprado 4 camisetas iguales y un jersey por un total de 70 €. Si cada camiseta le ha costado 12 €, ¿cuánto le ha costado el jersey? 12 En un jardín hay 40 rosales. Un quinto es de rosas rojas, un cuarto de rosas blancas y el resto de rosas amarillas. ¿Cuántos rosales con rosas amarillas hay en el jardín? Problemas REPASO ACUMULATIVO 9 141 ES0000000024590 663006-Unidad 09_22592.indd 141 10/03/2015 13:23:19 UNIDAD 9 2 •  c 5 21, r 5 2 •  c 5 18, r 5 6 •  c 5 416, r 5 2 •  c 5 297, r 5 4 •  c 5 1.022 •  c 5 2.230, r 5 32 3 • 15 2 9 2 3 5 3 • 4 1 8 2 2 5 10 • 24 2 3 2 5 5 16 • 10 2 6 1 9 5 13 • 6 2 2 1 4 5 8 • 12 2 2 1 7 5 17 • 6 3 2 2 5 5 7 • 3 3 4 2 8 5 4 4 • Dos tercios •  Seis octavos •  Tres quintos •  Siete novenos •  La fracción 7 9 . • La fracción 2 3 . 5 •  2 5        •  3 7        •  7 9 •  3 7        •  6 9        •  7 10 6 (75 1 65 1 32) 2 2 (20 1 15 1 9) 5 128 Han quedado 128 yogures. 7 75 3 3 5 225 225 2 180 5 45 Le sobran 45 baldosas. 8 1/3 de 120 5 40 120 2 (40 1 35) 5 45 € Le quedaron 45 €. 9 1/5 de 450 5 90 450 2 90 5 360 No van 360 alumnos. 10 (48 1 72) : 4 5 30 En cada una pondrá 30 zumos. 11 70 2 4 3 12 5 22 El jersey le ha costado 22 €. 12  1 5 de 40 5 8 1 4 de 40 5 10 40 2 (8 1 10) 5 22 Hay 22 rosales amarillos. Repaso en común • Pida a los alumnos que realicen esta página de actividades de repaso y que anoten en sus cuadernos las actividades en las que han tenido alguna dificultad. Haga una puesta en común y para cada una de ellas pida a un alumno que salga a la pizarra y explique a sus compañeros cómo debería realizarse. La clase analizará su respuesta. Aproveche para concienciar a los alumnos de la importancia del repaso y de reflexionar sobre su aprendizaje. 73
Longitud10 Contenidos de la unidad SABER MEDIDA • El metro, el decímetro y el centímetro. • El milímetro. • El kilómetro, el hectómetro y el decámetro. SABER HACER MEDIDA • Reconocimiento del metro como unidad principal de longitud. • Identificación de los submúltiplos del metro y utilización de sus equivalencias con él y entre ellos. • Identificación de los múltiplos del metro y utilización de sus equivalencias con él y entre ellos. • Paso de medidas de forma compleja a incompleja y viceversa. • Ordenación de grupos de medidas. • Resolución de problemas reales donde aparezcan medidas de longitud. RESOLUCIÓN DE PROBLEMAS • Elección de la pregunta que hace que un problema se resuelva con dos operaciones. • Invención de un problema que se resuelva con unos cálculos dados y tenga una solución dada.   TAREA FINAL • Interpretar datos de altitudes. SABER SER FORMACIÓN EN VALORES • Valoración de la utilidad de las unidades de longitud. • Interés por la resolución de problemas reales. 74
BIBLIOTECA DEL PROFESORADO Programación didáctica de aula Recursos para la evaluación • Evaluación de contenidos. Unidad 10: pruebas de control B y A. • Evaluación trimestral. Pruebas B, A y E. • Evaluación por competencias. Prueba 10. •  Rúbrica. Unidad 10. Enseñanza individualizada • Plan de mejora. Unidad 10. • Programa de ampliación. Unidad 10. Proyectos de trabajo cooperativo • Proyecto del segundo trimestre. Recursos complementarios • Fichas para el desarrollo de la inteligencia. • Operaciones y problemas. Aprendizaje eficaz • Técnicas de estudio y presentación de exámenes. Proyectos interdisciplinares • Programa de Educación en valores. • Programa de Educación emocional. • Inteligencias múltiples. RECURSOS DIGITALES LibroMedia • Unidad 10: actividades y recursos. MATERIAL DE AULA Láminas OTROS MATERIALES DEL PROYECTO Cuaderno del alumno • Segundo trimestre. Unidad 10. Solución de problemas. Método DECA SUGERENCIA DE TEMPORALIZACIÓN Enero MarzoFebrero La temporalización de esta unidad y de las siguientes puede variar en función de las fechas de la Semana Santa. ES0000000024590 663006_Matematicas_4_GRAZ_24259 PRIMARIA PRIMARIA Matemáticas PRIMARIA ANDALUCÍAMatemáticas ANDALUCÍA Matemáticas ANDALUCÍA ES0000 000024 590 663006 _Matem aticas_4_GRA Z_2425 9.indd 1 04/03/2 015 11:21:19 ES0000000024593 663039_Cdno_Matematicas_4-2_22732 PRIMARIA Matemáticas Segundo trimestre Matemáticas Segundo trimestre PRIMARIA CUADERNO CUADERNO ES0000000024593 663039_Cdno_Matematicas_4-2_22732.indd 1 19/02/2015 16:56:18 75
10 Longitud Escalando montañas A Ignacio y a sus amigos les encanta escalar montañas. Hoy quieren ascender a la cima de una montaña cuya altura sea mayor de las que han escalado hasta ahora. Consultan el plano y entre todos eligen el pico Altomar. Ya están preparados para comenzar el camino y esperan batir su propio récord. ¡Buena escalada y buena suerte! Peñalón 2.490 m Altomar 3.120 m Montelado 4.390 m 142 ES0000000024590 663006-Unidad 10_22593.indd 142 10/03/2015 13:21:21 Peñalón 2.490 m Altomar 3.120 m Montelado 4.390 m Propósitos •  Reconocer situaciones de la vida real en las que se utilicen unidades de longitud. •  Recordar los conceptos básicos necesarios para el desarrollo   de la unidad. Previsión de dificultades •  Algunos alumnos pueden tener dificultad al pasar de unas unidades de longitud a otras. Recuerde cómo se multiplica y se divide por la unidad seguida de ceros. Puede ayudarles el escribir en fila todas las unidades que se vayan a trabajar, ordenadas de mayor a menor y,   si es necesario, indicar con flechas las relaciones entre ellas. •  Al establecer comparaciones   y realizar cálculos con medidas expresadas en distintas unidades, recuerde y razone con los alumnos que, para poder operar,   es necesario que las unidades   de medida sean las mismas. Trabajo colectivo sobre la lámina Haga que un alumno lea la lectura inicial y pídales que observen   en la lámina las montañas que hay representadas y digan cuál es su altura. Pregúnteles qué unidad de longitud se representa con la letra m y qué otras unidades de longitud conocen. 1 Montelado: cuatro mil trescientos noventa.  Altomar: tres mil ciento veinte. Peñalón: dos mil cuatrocientos noventa. 2 2.490 3.120 4.390 3 4.390 – 2.490 = 1.900  Es 1.900 m más alta. 4 1 km = 1.000 m    4 km = 4.000 m  Montelado tiene una altura  mayor que 4 km. 5 Si eligen escalar Altomar   es porque todas las que   han escalado hasta ahora tienen una altura inferior a 3.120 m. Otras formas de empezar •  Comente que en esta unidad vamos a medir longitudes: el largo, ancho   o alto de un objeto, la distancia entre dos objetos o lugares… Recuerde   que podemos utilizar distintos tipos de unidades, y pida a los alumnos que digan ejemplos de unidades de medida de cada tipo y que expliquen   con un ejemplo cómo se mide utilizando dicha unidad: –  Naturales (partes del cuerpo): palmos, pies, pasos… –  Arbitrarias (objetos elegidos por el grupo): un rotulador, un clip… –  Convencionales (iguales para todos): metro, centímetro, kilómetro… Señale las ventajas e inconvenientes de cada tipo de unidad (si todos obtenemos o no los mismos resultados, si necesitamos o no un instrumento para medir…). 76
1 ¿Cuál es la altura de cada montaña? Escribe cómo se lee. 2 Ordena la altura de las montañas de menor a mayor. 3 ¿Cuántos metros es más alta Montelado que Peñalón? 4 ¿A cuántos metros equivale 1 kilómetro? ¿Qué pico del dibujo tiene una altura mayor de 4 kilómetros? 5 EXPRESIÓN ORAL. Explica esta afirmación: Ignacio y sus amigos solo han escalado montañas con una altura inferior a 2.490 m. Lee, comprende y razona ¿Qué sabes ya? TAREA FINAL Interpretar datos de altitudes Al final de la unidad analizarás datos de altitudes de ciudades. Antes, estudiarás las unidades de longitud. SABER HACER El metro, el decímetro, el centímetro y el kilómetro El metro (m) es la unidad principal de longitud. Para medir longitudes pequeñas, usamos unidades menores que el metro: el decímetro (dm) y el centímetro (cm). Para medir distancias o longitudes grandes, usamos una unidad mayor que el metro: el kilómetro (km). Las equivalencias entre estas unidades son: 1 metro 5 10 decímetros 1 m 5 10 dm 1 metro 5 100 centímetros 1 m 5 100 cm 1 kilómetro 5 1.000 metros 1 km 5 1.000 m 1 Calcula y completa en tu cuaderno. ¿Cuántos decímetros son? 2 m 8 m 14 m ¿Cuántos centímetros son? 3 m 5 m 27 m ¿Cuántos metros son? 4 km 9 km 12 km 2 Utiliza la regla y traza en tu cuaderno. Un segmento de 6 cm. Un segmento de 1 dm. 143 ES0000000024590 663006-Unidad 10_22593.indd 143 10/03/2015 13:21:23 UNIDAD 10 ¿Qué sabes ya? Recuerde a los alumnos las equivalencias del metro con el decímetro, centímetro y kilómetro. Después, pídales que realicen las actividades de forma individual y corríjalas en común despejando las dudas que hayan podido surgir. 1 • 20 dm 80 dm 140 dm •  300 cm 500 cm 2.700 cm • 4.000 m 9.000 m 12.000 m 2 R. L. Notas Competencias •  Comunicación lingüística. Es importante que los alumnos conozcan y utilicen los términos matemáticos correctamente. Al realizar la actividad de Expresión oral, anímelos a razonar de forma clara sus ideas usando vocabulario relacionado con la longitud. •  Aprender a aprender. Comente con los alumnos la importancia que tiene el afianzar los conceptos aprendidos para poder avanzar con seguridad. Señale que en esta unidad van a seguir aprendiendo sobre la longitud y conocerán nuevas unidades de medida. Inteligencia lingüística 77
El metro, el decímetro y el centímetro 1 Expresa en la unidad que se indica y completa en tu cuaderno. En decímetros 1 m y 5 dm 5 m y 4 dm 2 m y 7 dm 7 m y 8 dm 3 m y 8 dm 9 m y 3 dm En centímetros 1 m y 15 cm 6 m y 7 cm 4 m y 40 cm 8 m y 8 cm 5 m y 72 cm 9 m y 9 cm 2 ¿Cuántos centímetros mide cada cuerda? Calcula y completa. 4 m, 8 dm y 5 cm 6 m, 7 dm y 2 cm 9 m, 8 dm y 5 cm El metro es la principal unidad de longitud. El decímetro y el centímetro son unidades de longitud menores que el metro. La cinta roja mide 1 centímetro de ancho y 1 decímetro de largo. 1 decímetro 5 10 centímetros 1 dm 5 10 cm El paraguas que tiene Miguel mide 1 metro. 1 metro 5 10 decímetros 5 100 centímetros 1 m 5 10 dm 5 100 cm m dm cm 1 0 m dm cm 1 0 0 El decímetro y el centímetro son unidades de longitud menores que el metro. 1 dm 5 10 cm 1 m 5 10 dm 5 100 cm EJEMPLO 1 m y 5 dm 5 10 dm 1 5 dm 5 … dm EJEMPLO 1 m y 15 cm 5 100 cm 1 15 cm 5 … cm 144 ES0000000024590 663006-Unidad 10_22593.indd 144 10/03/2015 13:21:24 Propósitos •  Conocer y utilizar las equivalencias entre el metro, decímetro   y centímetro. •  Resolver problemas con medidas de longitud. Sugerencias didácticas Para explicar. Exprese que el metro es la principal unidad de longitud   y que en muchas situaciones reales necesitamos unidades menores que él, como el decímetro y el centímetro. Escriba en la pizarra las equivalencias entre ellas y realice algún ejemplo sencillo de paso de unas a otras. Comente que cuando se trata de pasar una medida en forma compleja a incompleja hay que pasar todas   las medidas a la unidad que se desea y sumarlas. Actividades 1 •  15 dm •  54 dm •  27 dm •  78 dm •  38 dm •  93 dm •  115 cm •  607 cm •  440 cm •  808 cm •  572 cm •  909 cm 2 Azul: 485 cm.    Roja: 672 cm.  Verde: 985 cm. 3 •  2 dm •  3 dm •  6 dm •  41 dm •  70 dm •  90 dm •  3 m •  4 m •  5 m •  72 m •  81 m •  90 m •  2 m •  5 m •  8 m •  45 m •  60 m •  700 m 4 •  19 cm 5 10 cm 1 9 cm 5   5 1 dm 1 9 cm •  45 cm 5 40 cm 1 5 cm 5 5 4 dm 1 5 cm •  86 cm 5 80 cm 1 6 cm 5 5 8 dm 1 6 cm •  356 cm 5 300 1 50 + 6 5 5 3 m 1 5 dm + 6 cm •  745 cm 5 700 1 40 + 5 5 5 7 m 1 4 dm + 5 cm •  680 cm 5 600 cm 1 80 cm 5 5 6 m 1 8 dm Otras actividades •  Coloque una cinta métrica en vertical en la pared de la clase, pegada   con celo, de manera que el «cero» coincida con el suelo. Agrupe   a los alumnos por parejas y pídales que, por turnos, salgan a medirse   unos a otros. En cada caso, el niño «medidor» dirá el número que aparece   en la cinta (medida en centímetros), otro compañero lo escribirá en la pizarra y, en común, se expresará dicha medida en metros y centímetros, y en metros, decímetros y centímetros. Por ejemplo: Dirán: «Andrés mide 137 centímetros». Escribirán: 137 cm 5 1 m y 37 cm 5 1 m, 3 dm y 7 cm. 78
10 3 Expresa en la unidad indicada. En decímetros 20 cm 410 cm 30 cm 700 cm 60 cm 900 cm En metros 30 dm 720 dm 40 dm 810 dm 50 dm 900 dm En metros 200 cm 4.500 cm 500 cm 6.000 cm 800 cm 7.000 dm 4 Lee y completa en tu cuaderno. HAZLO ASÍ 43 cm 5 40 cm 1 3 cm 5 5 4 dm 1 3 cm 19 cm 5 … dm 1 … cm 45 cm 5 … dm 1 … cm 86 cm 5 … dm 1 … cm HAZLO ASÍ 257 cm 5 200 cm 1 50 cm 1 7 cm 5 5 2 m 1 5 dm 1 7 cm 356 cm 5 … m 1 … dm 1 … cm 745 cm 5 … m 1 … dm 1 … cm 680 cm 5 … m 1 … dm Problemas 5 Resuelve. Gabriel tiene una cometa roja y otra cometa verde. La cuerda de la cometa roja mide 8 m, 6 dm y 9 cm, y la cuerda de la cometa verde mide 7 m, 3 dm y 5 cm. ¿Cuántos centímetros mide la cuerda verde menos que la roja? ¿Cuántos centímetros le faltan a la cuerda roja para medir 9 m? Suma números de dos cifras sin llevar descomponiendo los sumandos 31 1 23 28 1 61 43 1 26 42 1 51 41 1 37 51 1 38 54 1 43 56 1 42 67 1 12 76 1 22 83 1 16 94 1 15 CÁLCULO MENTAL EJEMPLO 20 cm 5 2 dm : 10 EJEMPLO 30 dm 5 3 m : 10 EJEMPLO 200 cm 5 2 m : 100 24 1 52 5 70 1 6 5 76 145 ES0000000024590 663006-Unidad 10_22593.indd 145 10/03/2015 13:21:25 UNIDAD 10 5   •  Roja: 869 cm. Verde: 735 cm. 869 2 735 5 134 La cuerda verde mide 134 cm menos que la roja. •  9 m 5 900 cm 900 2 869 5 31 Para medir 9 m a la cuerda roja le faltan 31 cm. Cálculo mental •  54 •  89 •  69 •  93 •  78 •  89 •  97 •  98 •  79 •  98 •  99 •  109 Notas Otras actividades •  Nombre en común ejemplos de longitudes de objetos que podamos medir en metros, en decímetros y en centímetros. Después, pida a los alumnos que midan algunos objetos que se encuentren en la clase: el largo de un lapicero, el ancho de la mesa, el largo de la pizarra…, utilizando la regla para medir en centímetros y la cinta métrica para hacerlo en metros. Anímelos a estimar la medida antes de realizar la medición. Al final, haga una puesta en común, escriba en la pizarra las medidas obtenidas y exprese, de forma colectiva, dichas medidas en varias unidades, trabajando las equivalencias presentadas en esta doble página. 79
En metrosEn centímetros El milímetro 1 Expresa en milímetros y completa en tu cuaderno. 3 cm 7 cm 12 cm 48 cm 2 m 5 m 32 m 58 m 5 cm y 8 mm 9 cm y 4 mm 5 m y 7 mm 6 m y 3 mm 2 Expresa en la unidad que se indica. 30 mm 120 mm 500 mm 80 mm 430 mm 800 mm 4.000 mm 84.000 mm 7.000 mm 92.000 mm El milímetro es una unidad de longitud menor que el centímetro. El milímetro lo usamos para medir longitudes muy pequeñas. El clip mide 7 milímetros de ancho y 3 centímetros y 2 milímetros de largo. 1 centímetro 5 10 milímetros 1 cm 5 10 mm 1 metro 5 1.000 milímetros 1 m 5 1.000 mm m dm cm mm 1 0 m dm cm mm 1 0 0 0 El milímetro es una unidad de longitud menor que el centímetro. 1 cm 5 10 mm 1 m 5 1.000 mm RECUERDA 1 cm 5 10 mm 1 m 5 1.000 mm EJEMPLO 30 mm 5 3 cm : 10 EJEMPLO 4.000 mm 5 4 m : 1.000 146 ES0000000024590 663006-Unidad 10_22593.indd 146 10/03/2015 13:21:26 Propósitos •  Reconocer el milímetro como   una unidad de longitud menor   que el centímetro •  Utilizar las equivalencias entre centímetro y metro con el milímetro. Sugerencias didácticas Para explicar. Lea la situación inicial y comente que a veces es necesario utilizar una unidad más pequeña   que el centímetro: el milímetro. Escriba su nombre y abreviatura en la pizarra. Pida a los alumnos que observen   la regla e indíqueles la señalización de los centímetros y milímetros y pídales que cuenten cuántos milímetros tiene un centímetro. Escriba en la pizarra   las equivalencias del centímetro   y el metro con el milímetro. Para reforzar. Pida a los alumnos que preparen un cuadro en el que aparezcan el metro y sus submúltiplos y las equivalencias que han trabajado. Anímelos a ser creativos. Actividades 1   •  30 mm •  2.000 mm •  70 mm •  5.000 mm •  120 mm •  32.000 mm •  480 mm •  58.000 mm •  58 mm •  94 mm •  5.007 mm •  6.003 mm 2   •  3 cm •  12 cm •  50 cm •  8 cm •  43 cm •  80 cm •  4 m •  84 m •  7 m •  92 m 3   •  19 mm 5 10 mm 1 9 mm 5   5 1 cm 1 9 mm •  28 mm 5 20 mm 1 8 mm 5  5 2 cm 1 8 mm •  45 mm 5 40 mm 1 5 mm 5  5 4 cm 1 5 mm 4 •  37 mm , 39 mm , 40 mm •  56 mm , 60 mm , 540 mm •  85 mm , 90 mm , 750 mm Otras actividades •  Forme grupos de 4 o 5 alumnos y entregue a cada grupo un folio para   que cada alumno trace libremente, con un rotulador de distinto color,   una línea recta utilizando una regla. A continuación, indíqueles que comparen las líneas dibujadas y que estimen cuál es la más larga y la más corta, cuáles miden menos y más de 1 decímetro… Por último, indíqueles que midan   con la regla la longitud de cada línea y den el resultado, primero, en milímetros y, después, en centímetros y milímetros. 80
MARIQUITA 7 mm SALTAMONTES 3 cm y 5 mm HORMIGA 5 mm GUSANO 7 cm y 9 mm 10 Lee y contesta. Javier ha sumado dos de estas longitudes y ha obtenido como resultado 4 cm. ¿Qué dos longitudes ha sumado Javier? RAZONAMIENTO 3 Completa en tu cuaderno. 19 mm 5 … cm 1 … mm 28 mm 5 … cm 1 … mm 45 mm 5 … cm 1 … mm 4 Expresa en milímetros y ordena las longitudes de cada grupo de menor a mayor. Problemas 5 Lee y resuelve. Daniela está leyendo un artículo sobre la longitud de algunos animales. ¿Cuántos milímetros en total miden una mariquita y una hormiga? ¿Cuántos centímetros y milímetros son? ¿Cuántos milímetros mide un saltamontes? ¿Cuántos milímetros mide un saltamontes más que una mariquita? ¿Cuántos milímetros mide un gusano de seda más que un saltamontes? HAZLO ASÍ 39 mm 4 cm 3 cm y 7 mm 5 cm y 6 mm 8 cm y 5 mm 6 cm 54 cm 9 cm 75 cm 2 cm y 5 mm 20 mm 15 mm 3 cm 75 mm 5 70 mm 1 5 mm 5 5 7 cm 1 5 mm 147 ES0000000024590 663006-Unidad 10_22593.indd 147 10/03/2015 13:21:28 Inteligencia naturalista UNIDAD 10 5 • 7 mm 1 5 mm 5 12 mm 5 5 1 cm 1 2 mm Miden 12 mm; 1 cm y 2 mm. • 30 mm 1 5 mm 5 35 mm Un saltamontes mide 35 mm. • 35 mm 2 7 mm 5 28 mm Un saltamontes mide 28 mm más que una mariquita. • 79 mm 2 35 mm 5 44 mm Un gusano de seda mide 44 mm más que un saltamontes. Razonamiento Expresamos todas las medidas en milímetros y calculamos. 25 mm   20 mm   15 mm   30 mm 4 cm 5 40 mm 5 25 mm 1 15 mm Javier ha sumado 2 cm y 5 mm y 15 mm. Notas Otras actividades • Fomente en los alumnos la estimación de longitudes de objetos cotidianos. Al principio, pueden tener a la vista una regla y una cinta métrica y quitar posteriormente dicho apoyo. Propóngales que estimen las siguientes longitudes en la unidad indicada, y después las midan para comprobar dicha estimación: –  En centímetros, el largo de un bolígrafo y el ancho de la mesa. – En milímetros, el grosor de un libro y el lado de un cuadradito del cuaderno. –  En metros, el ancho de la puerta y el largo de la clase. 81
El kilómetro, el hectómetro y el decámetro 1 Expresa en metros y completa en tu cuaderno. 2 dam 14 dam 4 dam 25 dam 3 hm 15 hm 4 hm 37 hm 7 km 58 km 9 km 95 km 2 Expresa en metros. 3 dam y 5 m 7 dam y 8 m 12 dam y 7 m 34 dam y 9 m 4 hm y 16 m 6 hm y 25 m 15 hm y 6 m 29 hm y 8 m 6 km y 462 m 8 km y 175 m 17 km y 92 m 45 km y 5 m 3 Calcula y expresa en la unidad que se indica. En decámetros En hectómetros En kilómetros 20 m 80 m 50 m 90 m 400 m 700 m 600 m 800 m 3.000 m 6.000 m 4.000 m 8.000 m El kilómetro, el hectómetro y el decámetro son unidades de longitud mayores que el metro y se utilizan para medir distancias o longitudes muy grandes. Fíjate en las relaciones de estas unidades con el metro. 1 kilómetro 5 1.000 metros 1 km 5 1.000 m 1 hectómetro 5 100 metros 1 hm 5 100 m 1 decámetro 5 10 metros 1 dam 5 10 m km hm dam m 1 0 0 0 km hm dam m 1 0 0 km hm dam m 1 0 El kilómetro, el hectómetro y el decámetro son unidades de longitud mayores que el metro. 1 km 5 1.000 m 1 hm 5 100 m 1 dam 5 10 m RECUERDA 1 dam 5 10 m 1 hm 5 100 m 1 km 5 1.000 m EJEMPLO 20 m 5 2 dam : 10 EJEMPLO 400 m 5 4 hm : 100 EJEMPLO 3.000 m 5 3 km : 1.000 148 ES0000000024590 663006-Unidad 10_22593.indd 148 10/03/2015 13:21:29 Propósitos •  Reconocer el kilómetro, el hectómetro y el decámetro como unidades de longitud mayores   que el metro. •  Conocer y aplicar las equivalencias entre el metro y sus múltiplos. •  Resolver problemas con unidades de longitud. Sugerencias didácticas Para explicar. Comente con los alumnos que para medir longitudes grandes utilizamos unidades mayores que el metro. Escriba en la pizarra   las tres unidades y sus abreviaturas. Explique la equivalencia de cada  unidad con el metro y pida   a los alumnos que las memoricen. Para reforzar. Pida a los alumnos que preparen un cuadro en el que aparezcan el metro y sus múltiplos   y sus equivalencias. Actividades 1 •  20 m •  140 m •  40 m •  250 m •  300 m •  1.500 m •  400 m •  3.700 m •  7.000 m •  58.0000 m •  9.000 m •  95.000 m 2 •  35 m •  416 m •  78 m •  625 m •  127 m •  1.506 m •  349 m •  2.908 m •  6.462 m •  8.175 m •  17.092 m •  45.005 m 3 •  2 dam •  8 dam •  5 dam •  9 dam •  4 hm •  7 hm •  6 hm •  8 hm •  3 km •  6 km •  4 km •  8 km 4 •  56 m 5 5 dam 1 6 m •  64 m 5 6 dam 1 4 m •  72 m 5 7 dam 1 2 m •  89 m 5 8 dam 1 9 m Otras actividades •  Lleve a clase un mapa de carreteras y comente que en él están indicadas, en kilómetros, las distancias entre ciudades y pueblos. Haga una fotocopia de la zona del mapa donde se encuentre su localidad y repártala por grupos a los alumnos, para realizar ejercicios de interpretación: preguntándoles,   por ejemplo, qué distancia hay entre dos localidades concretas,   para que la expresen en kilómetros y en metros. •  Fotocopie y entregue a los alumnos una tabla de distancias entre   las capitales de provincia de España, explique con un ejemplo cómo  se maneja y busque en común la distancia entre dos ciudades  conocidas por los alumnos. 82
4 Descompón cada medida usando el mayor número de unidades posible. 56 m 72 m 64 m 89 m 278 m 698 m 583 m 810 m 1.367 m 5.309 m 2.876 m 7.012 m Problemas 5 Observa el plano y resuelve. ¿Cuántos metros mide cada camino? Paula va de la ciudad A a la ciudad B por el camino más corto y vuelve a la ciudad A por el más largo. ¿Cuántos metros recorre Paula en total? Ramiro vive en la ciudad B. Cada día va a la ciudad A por el camino verde y vuelve a la ciudad B por el mismo camino. ¿Cuántos metros recorre cada día? ¿Cuántos kilómetros y metros son? Cada día, un autobús sale de la ciudad A a la ciudad B por la ruta roja y para a la mitad del camino. ¿A cuántos kilómetros de la ciudad B tiene la parada? Inventa un camino de dos tramos de la ciudad A a la ciudad B cuya longitud sea de 2 km. 10 4 Descompón cada medida usando el mayor número de unidades posible. 56 m 72 m 64 m 89 m 278 m 698 m 583 m 810 m 1.367 m 5.309 m 2.876 m 7.012 m Problemas 5 Observa el plano y resuelve. ¿Cuántos metros mide cada camino? Paula va de la ciudad A a la ciudad B por el camino más corto y vuelve a la ciudad A por el más largo. ¿Cuántos metros recorre Paula en total? Ramiro vive en la ciudad B. Cada día va a la ciudad A por el camino verde y vuelve a la ciudad B por el mismo camino. ¿Cuántos metros recorre cada día? ¿Cuántos kilómetros y metros son? Cada día, un autobús sale de la ciudad A a la ciudad B por la ruta roja y para a la mitad del camino. ¿A cuántos kilómetros de la ciudad B tiene la parada? Inventa un camino de dos tramos de la ciudad A a la ciudad B cuya longitud sea de 2 km. Suma números de dos cifras llevando descomponiendo los sumandos 32 1 28 23 1 47 47 1 13 45 1 35 41 1 39 51 1 39 56 1 14 54 1 16 62 1 18 69 1 21 68 1 22 74 1 26 CÁLCULO MENTAL HAZLO ASÍ 75 m 5 70 m 1 5 m 5 7 dam 1 5 m 346 m 5 300 m 1 40 m 1 6 m 5 3 hm 1 4 dam 1 6 m 8.273 m 5 8.000 m 1 200 m 1 70 m 1 3 5 8 km 1 2 hm 1 7 dam 1 3 m 36 1 24 5 50 1 10 5 60 49 km 41km 25 hm 125m 39 km y725 m 40 km y 5 hm 36 km y 5 hm 37kmy12dam 32 km 20 km 75 dam A B 149 ES0000000024590 663006-Unidad 10_22593.indd 149 10/03/2015 13:21:34 UNIDAD 10 • 278 m 5 2 hm 1 7 dam 1 8 m • 583 m 5 5 hm 1 8 dam 1 3 m • 698 m 5 6 hm 1 9 dam 1 8 m • 810 m 5 8 hm 1 1 dam • 1.367 m 5 1 km 1 3 hm 1 1 6 dam 1 7 m • 2.876 m 5 2 km 1 8 hm 1 1 7 dam 1 6 m • 5.309 m 5 5 km 1 3 hm 1 9 m • 7.012 m 5 7 km 1 1 dam 1 2 m 5 • Verde: 39.725 m 1 36.500 m 1 1 20.000 m 1 750 m 5 5 96.975 m Rojo: 41.000 m 1 2.500 m 1 1 125 m 5 43.625 m Azul: 40.500 m 1 49.000 m 1 1 32.000 m 1 37.120 m 5 5 158.620 m • 43.625 m 1 158.620 m 5 5 202.245 m 5 202 km y 245 m • 96.975 m 3 2 5 193.950 m 5 5 193 km y 950 m • 43.625 : 2 c 5 21.812, r 5 1 21.812 m 5 21 km y 812 m El autobús tiene la parada a 21 km y 812 m de la ciudad B. • R. L. Cálculo mental •  60 •  70 •  60 •  80 •  80 •  90 •  70 •  70 •  80 •  90 •  90 •  100 Notas Competencias •  Conciencia y expresión cultural. La interpretación de croquis es un procedimiento muy importante que aúna las Matemáticas y los contenidos artísticos. Comente con los alumnos las características de los croquis, mostrando que son dibujos aproximados en los que recogemos distintas informaciones. Pídales que creen uno ellos mismos a partir de una descripción dada por usted y plantee después distintas actividades similares a las trabajadas. 83
Elige la pregunta para que el problema se resuelva con dos operaciones y resuelve. 1 En las rebajas, Marina compró 3 chándales a 24 € cada uno y unas deportivas por 35 €. Preguntas A. ¿Cuánto le costaron las deportivas más que un chándal? B. ¿Cuánto le costaron en total los chándales? C. ¿Cuánto se gastó en total Marina? 2 Luis lleva en su furgoneta 100 cajas de refrescos. En el primer supermercado deja 15 cajas y el resto las reparte en partes iguales entre otros 5 supermercados. Preguntas A. ¿Cuántas cajas lleva después de salir del primer supermercado? B. ¿Cuántas cajas de refrescos deja en cada supermercado? C. ¿Cuántos refrescos reparte entre los 5 supermercados? Vamos a leer el problema y las preguntas dadas. Después, elegimos la pregunta para que el problema se resuelva con dos operaciones. A Raquel le han regalado un juego de construcción con 75 piezas rojas, 80 azules y 95 amarillas. Ha utilizado la mitad de las piezas para hacer un robot. Preguntas A. ¿Cuántas piezas tiene el juego en total? B. ¿Cuántas piezas amarillas más que rojas tiene el juego? C. ¿Cuántas piezas utilizó Raquel para hacer el robot? La pregunta que se responde con dos operaciones es la C. 1.º Calcula las piezas que tiene el juego en total. 75 1 80 1 95 5 250 2.º Calcula las piezas que utiliza para hacer el robot. 250 : 2 5 125 Solución: Raquel ha utilizado 125 piezas para hacer el robot. Elegir la pregunta para que el problema se resuelva con dos operaciones Solución de problemas 150 ES0000000024590 663006-Unidad 10_22593.indd 150 10/03/2015 13:21:40 Propósitos •  Elegir la pregunta para que un problema se resuelva con dos operaciones. •  Inventar problemas que se resuelvan con unos cálculos dados y que tengan una solución dada. Sugerencias didácticas Para explicar. Lea el problema   y las preguntas y explique   a los alumnos que debemos elegir   la pregunta para que el problema   se resuelva con dos operaciones.   Lea cada pregunta, pídales qué digan qué operación u operaciones hay que realizar para responderla y pregúnteles cuál es la pregunta correcta. Actividades 1 C. ¿Cuánto se gastó en total?   3 3 24 5 72  72 1 35 5 107  Marina se gastó 107 €. 2 B. ¿Cuántas cajas de refrescos deja en cada supermercado?  100 2 15 5 85  85 : 5 5 17  En cada supermercado deja   17 cajas. 3 R. M. ¿Cuántos kilos de tomates le quedaron?  12 3 6 5 72; 72 2 10 5 62  Le quedaron 62 kilos. 4 R. M. ¿Cuántas canciones   ha grabado en total?  32 3 4 5 128   128 1 19 5 147   Ha grabado 147 canciones. 5 R. M. ¿Cuántas monedas  le han dado en total?  100 1 50 5 150; 150 : 25 75  Le han dado 75 monedas. 6 R. M. ¿Cuántos metros medía cada trozo?  40 2 4 5 36; 36 : 9 5 4  Cada trozo medía 4 metros. 7 R. M. ¿Cuántas llamadas atendió el domingo Nuria?  124 1 72 5 196; 196 : 25 98  Atendió 98 llamadas. Otras actividades •  Presente a los alumnos algunos textos para que inventen problemas  de dos operaciones, utilizando algunos datos del texto. Corríjalos  al final de forma colectiva. Dícteles por ejemplo el siguiente texto y pídales que inventen un problema   de suma y resta, otro de suma y multiplicación y otro de suma y división: «Las tres clases de 4.º han organizado un viaje de 5 días para visitar  los principales monumentos de su comunidad. En total van 60 alumnos:   20 de 4.º A, 18 de 4.º B y el resto de 4.º C. El precio del viaje por persona es: 45 € el alojamiento y 40 € la comida, además de 50 € de transporte». 84
Escribe un problema que se resuelva con cada grupo de cálculos y tenga la solución dada. 1 3 10 Lee y escribe una pregunta para que el problema se resuelva con dos operaciones. Después, resuélvelo. 3 Lucía recogió en su huerto 12 cajas con 6 kilos de tomates cada una y regaló 10 kilos de tomates a su amiga. 4 Miguel ha grabado 4 CD de música, con 32 canciones cada uno, y 1 CD, con 19 canciones. 5 Gustavo necesita monedas de 2 € para su tienda. Ha ido al banco a cambiar un billete de 100 € y otro de 50 € por monedas de 2 €. 6 Para hacer disfraces, Susana compró 40 m de cinta. Primero cortó 4 m y el resto lo partió en 9 trozos iguales. 7 Nuria es recepcionista de un hotel. El sábado atendió 125 llamadas por la mañana y 72 por la tarde. El domingo atendió la mitad de llamadas que el sábado. 8 Para pagar una factura, Javier ha entregado 7 billetes de 50 € y un billete de 20 €. INVENTA TUS PROBLEMAS Escribe un problema que se resuelva con cada grupo de cálculos y tenga la solución dada. 1 3 12 1 23 1 35 5 70 70 3 15 5 1.050 Solución: Por los jerséis recibidos en su tienda, Ana pagó 1.050 €. 90 2 15 5 75 75 : 3 5 25 Solución: Cada cinturón le costó 25 €. 28 1 20 5 48 48 : 6 5 8 Solución: En cada frutero Pablo ha puesto 8 piezas de fruta. 2 Camiseta 15 € 151 ES0000000024590 663006-Unidad 10_22593.indd 151 10/03/2015 13:21:42 UNIDAD 10 8 R. M. ¿Cuál es el importe total de la factura? 7 3 50 5 350; 350 1 20 5 370 El importe total de la factura es de 370 €. Inventa tus problemas 1 R. M. Ana ha recibido en su tienda 12 jerséis rojos, 23 azules y 35 verdes. Cada jersey cuesta 15 €. ¿Cuánto ha pagado en total? 2 R. M. Pablo tenía 28 manzanas y 20 peras. Las ha repartido en partes iguales en 6 fruteros. ¿Cuántas piezas de fruta ha puesto en cada frutero? 3 R. M. Marta tenía 90 €. Compró una camiseta por 15 € y con el resto de su dinero compró 3 cinturones iguales. ¿Cuánto le costó cada cinturón? Notas Competencias •  Iniciativa y emprendimiento. El programa de invención de problemas es un contexto muy adecuado para el desarrollo de esta competencia. Anime a los alumnos a ser creativos a la hora de crear los problemas y de exponerlos a sus compañeros, sin abandonar por ello la corrección matemática. Valore sus logros y muéstreles cómo sus capacidades van aumentado con la práctica. 85
6 Expresa en metros. 2 dam y 6 m 5 hm y 4 m 4 dam y 3 m 2 km y 145 m 3 hm y 25 m 7 km y 90 m 7 Expresa en la unidad indicada. En dam: 40 m 80 m 190 m En hm: 300 m 700 m 1.500 m En km: 5.000 m 9.000 m 21.000 m 8 Expresa cada medida usando el mayor número de unidades posible. Fíjate en los ejemplos. 63 cm 89 cm 95 cm 163 cm 489 cm 720 cm 134 m 568 m 712 m 2.789 m 4.720 m 6.914 m 9 Observa el dibujo y ordena. De menor a mayor, la longitud de estos rollos de cinta. De mayor a menor, las distancias recorridas por estas motos. 1 VOCABULARIO. Escribe el nombre de las unidades que se indican. Tres unidades de longitud menores que el metro. Tres unidades de longitud mayores que el metro. 2 Copia y completa en tu cuaderno. 1 m 5 … dm 23 m 5 … mm 7 m 5 … cm 45 m 5 … mm 1 dm 5 … cm 14 dm 5 … cm 8 dm 5 … cm 31 m 5 … cm 1 cm 5 … mm 62 cm 5 … mm 9 cm 5 … mm 74 cm 5 … mm 3 Expresa en metros. 10 dm 300 cm 2.000 mm 40 dm 600 cm 5.000 mm 70 dm 800 cm 9.000 mm 4 Expresa en la unidad que se indica. 4 m, 5 dm y 7 cm 2 m, 6 dm y 9 cm 17 m, 8 dm y 9 cm 3 m, 8 cm y 5 mm 5 m, 4 cm y 6 mm 14 m, 9 cm y 7 mm 5 Ordena cada grupo de medidas de mayor a menor. 4.000 mm 41 dm 4 m y 9 cm 9 dm y 5 cm 960 cm 9.000 mm 3 m y 2 dm 330 cm 34 dm 7.000 mm 690 cm 68 dm ACTIVIDADES En centímetros En milímetros EJEMPLO 257 cm 5 200 cm 1 50 cm 1 7 cm 5 5 2 m 1 5 dm 1 7 cm 468 m 5 400 m 1 60 m 1 8 m 5 5 4 hm 1 6 dam 1 8 m 24 km y 15 hm 3 m y 80 dm 2 dam y 9 m 1 hm y 20 dam 76 km y 9 dam 58 km y 7 hm 152 ES0000000024590 663006-Unidad 10_22593.indd 152 10/03/2015 13:21:43 Propósitos •  Repasar los contenidos básicos   de la unidad. Actividades 1 •  Decímetro, centímetro   y milímetro. •  Decámetro, hectómetro   y kilómetro. 2 •  10 dm •  23.000 mm •  700 cm •  45.000 mm •  10 cm •  140 cm •  80 cm •  3.100 cm •  10 mm •  620 mm •  90 mm •  740 mm 3 •  1 m •  3 m •  2 m •  4 m •  6 m •  5 m •  7 m •  8 m •  9 m 4 •  457 cm •  269 cm •  1.789 cm •  3.085 mm •  5.046 mm •  14.097 mm 5 •  41 dm . 4 m y 9 cm . 4.000 mm •  960 cm . 9.000 mm .   . 9 dm y 5 cm •  34 dm . 330 cm . 3 m y 2 dm •  7.000 mm . 690 cm . 68 dm 6 •  26 m •  504 m •  43 m •  2.145 m •  325 m •  7.090 m 7 •  4 dam 8 dam 19 dam •  3 hm 7 hm 15 hm •  5 km 9 km 21 km 8 •  6 dm 1 3 cm •  8 dm 1 9 cm •  9 dm 1 5 cm •  1 m 1 6 dm 1 3 cm •  4 m 1 8 dm 1 9 cm •  7 m 1 2 dm •  1 hm 1 3 dam 1 4 m •  5 hm 1 6 dam 1 8 m •  7 hm 1 1 dam 1 2 m •  2 km 1 7 hm 1 8 dam 1 9 m •  4 km 1 7 hm 1 2 dam •  6 km 1 9 hm 1 1 dam 1 4 m Otras actividades •  Escriba en la pizarra un cuadro con las abreviaturas de las unidades  de longitud trabajadas, ordenadas de mayor a menor. Pregunte y escriba  en cada caso en las flechas de arriba qué operación hacemos  para pasar de una unidad a otra. Después, comente que cada unidad  es 10 veces la siguiente y complete el resto de las equivalencias. 3 10 3 10 3 10 3 10 3 10 3 10 km hm dam m dm cm mm 3 1.0003 1.000 3 1003 100 3 103 10 86
12 Resuelve. Micaela mira el plano de los nuevos pisos que van a construir en su barrio. ¿Cuántos metros de largo mide la habitación A? ¿Cuántos centímetros son? ¿Cuántos metros de ancho mide la habitación B? ¿Y el baño? El salón tiene un rodapié de madera. ¿Cuántos metros de rodapié tiene si el ancho de la puerta es de 1 m y 90 cm? En la habitación B hay un armario empotrado en la pared que mide 6 m. El armario mide de ancho 1 m, 4 dm y 5 cm. ¿Cuántos centímetros de pared quedan libres? Problemas 10 Lee y resuelve. Virginia va a poner en la cocina un lavavajillas de 6 dm de ancho, un mueble de 6 dm y 8 cm de ancho y una lavadora de 65 cm de ancho. ¿Cuántos metros y centímetros ocuparán si los coloca todos unidos en fila? Pablo tiene un póster, de 3 dm y 5 cm de ancho y 1 m y 5 cm de alto, y le pone un listón de madera alrededor. ¿Cuántos centímetros de listón necesita? 11 Resuelve. La montaña más alta del mundo es el Everest, cuya altura es de 8.848 m, y la altura de la segunda montaña más alta es de 2 hm, 3 dam y 7 m menos. ¿Cuántos metros de altura tiene la segunda montaña más alta del mundo? 10 13 Miguel mide 1 m y 35 cm. Paula le dice a su hermano Miguel: «Si me subo a un taburete de 15 cm de altura y tú te agachas 1 dm, mido igual que tú». ¿Cuál es la altura de Paula? Demuestra tu talento Habitación B Habitación A Baño Salón Cocina 3 m 6 m 4 m 6 m 3m2m 2m 12 Resuelve. Micaela mira el plano de los nuevos pisos que van a construir en su barrio. ¿Cuántos metros de largo mide la habitación A? ¿Cuántos centímetros son? ¿Cuántos metros de ancho mide la habitación B? ¿Y el baño? El salón tiene un rodapié de madera. ¿Cuántos metros de rodapié tiene si el ancho de la puerta es de 1 m y 90 cm? En la habitación B hay un armario empotrado en la pared que mide 6 m. El armario mide de ancho 1 m, 4 dm y 5 cm. ¿Cuántos centímetros de pared quedan libres? 153 ES0000000024590 663006-Unidad 10_22593.indd 153 10/03/2015 13:21:46 UNIDAD 10 9 • 3 m y 80 dm , 2 dam y 9 m , , 1 hm y 20 dam • 76 km y 9 dam . . 58 km y 7 hm . . 24 km y 15 hm 10 • 60 cm 1 68 cm 1 65 cm 5 5 193 cm 5 1 m y 93 cm Ocupan 1 m y 93 cm. • 35 3 2 1 105 3 2 5 280 Necesita 280 cm de listón. 11  8.848 2 237 5 8.611 Mide 8.611 m. 12  • Habitación A: 4 m 5 400 cm. • Habitación B: 2 m. Baño: 2 m. • 2 3 6 1 2 3 3 2 1,9 5 16,1 Necesita 16,1 m de listón. • 600 2 145 5 455 Quedan libres 455 cm. Demuestra tu talento 13  Miguel mide 135 cm. 135 2 10 2 15 5 110 cm La altura de Paula es 110 cm. Notas Competencias •  Competencia social y cívica. La casa y lo que se refiere a ella es un contexto muy familiar y motivador para los alumnos. Suscite un debate sobre temas relacionados con la casa como el respeto por los demás, la colaboración en las tareas del hogar, la convivencia con los vecinos… Puede pedirles también que hagan un croquis parecido de sus casas y realicen actividades similares a las planteadas. Inteligencia espacial 87
Interpretar datos de altitudes Hoy en clase han hecho un esquema comparando altitudes de ciudades. En él aparece la ciudad de mayor altitud del mundo, La Rinconada, y la altitud a la que están algunas ciudades españolas. 1 Descompón la altitud de cada ciudad y exprésala usando todas las unidades de longitud posibles. Ávila Madrid Sevilla 2 Observa y resuelve. ¿Cuál es la altitud de Madrid menos que la de La Rinconada en metros? ¿Cuántos kilómetros y metros son? ¿Cuánto es la altitud de Madrid más que la de Sevilla en metros? ¿Cuántos hectómetros y metros son? Virginia vive en Ávila y va a Sevilla a visitar a una amiga. ¿Cuántos metros tiene que descender? ¿Cuántos kilómetros y metros son? Jaime vive en Madrid y hoy tiene que ir a Ávila. ¿Cuántos metros tiene que ascender? ¿Cuántos hectómetros y metros son? 3 TRABAJO COOPERATIVO. Buscad y plantead. Averigua con tu compañero la altitud de otras ciudades y plantead problemas similares a los propuestos en esta página. Después, resolvedlos. SABER HACER EJEMPLO La Rinconada: 5.099 m 5 … m 1 … m 1 … m 5 … km 1 … 1 … Ávila: 1.131 m Madrid: 655 m Sevilla: 11 m La Rinconada: 5.099 m 154 ES0000000024590 663006-Unidad 10_22593.indd 154 10/03/2015 13:21:48 Propósitos •  Desarrollar la competencia matemática resolviendo una situación de la vida real. Actividades pág. 154 1 La Rinconada: 5.099 m 5 5 5 km 1 9 dam 1 9 m • Ávila: 1.131 m 5 5 1 km 1 1 hm 1 3 dam 1 1 m • Madrid: 655 m 5 5 6 hm 1 5 dam 1 5 m • Sevilla: 11 m 5 1 dam 1 1 m 2 • 5.099 2 655 5 4.444 4.444 m 5 4 km 1 444 m • 655 2 11 5 644 644 m 5 6 hm y 44 m • 1.131 2 11 5 1.120 1.120 m 5 1 km 1 120 m • 1.131 2 655 5 476 476 m 5 4 hm 1 76 m 3 R. L. Haga una puesta en común con las altitudes buscadas por los alumnos y proponga actividades similares a las propuestas en esta página. Actividades pág. 155 1 • 4.448 • c 5 120, r 5 20 • 107.298 • c 5 95 • 140.217 • c 5 107 2 • 12 2 6 1 5 5 11 • 16 1 4 2 6 5 14 • 28 2 5 5 23 • 2 1 12 5 14 • 18 2 3 3 2 5 12 • 15 : 3 1 8 5 13 • 15 2 6 2 5 5 4 •  6 2 3 1 8 5 11 3 • 138 • 2.000 • 160 • 2.400 4 •  3 10 5 0,3 •  32 100 5 0,32 •  12 10 5 1,2 •  326 1.000 5 0,326 •  9 100 5 0,09 •  87 1.000 5 0,087 Desarrollo de la competencia matemática •  El trabajo de esta página se centra en la aplicación de todo lo aprendido en la unidad a datos de altitudes de distintas localidades. De esta manera, los alumnos comprenderán la utilidad de sus saberes y podrán desarrollar de manera adecuada esta competencia. A la hora del trabajo cooperativo, pida a los alumnos que antes de llevarlo a cabo realicen una planificación cuidadosa por escrito de todos los pasos que van a realizar: dónde van a buscar información, cómo la van a exponer a sus compañeros, de qué forma van a plantear los problemas, en qué formato expondrán los resultados… Comente esas planificaciones con los grupos. Inteligencia interpersonal 88
4 Escribe en forma de fracción y en forma decimal. 3 décimas 32 centésimas 12 décimas 326 milésimas 9 centésimas 87 milésimas 5 Escribe cómo se leen de dos formas. 8,9 3,78 4,621 32,5 15,03 7,072 6 Coloca los números y calcula. 3,56 1 21,9 1 134,8 5,7 1 45,078 1 72,6 31,8 2 9,79 32 3 1,4 498,4 2 76,762 27,5 3 100 1 Calcula. 278 3 16 2.780 : 23 1.987 3 54 5.890 : 62 607 3 231 7.811 : 73 2 Calcula estas operaciones. 12 2 2 3 3 1 5 18 2 (9 : 3) 3 2 16 1 8 : 2 2 6 (6 1 9) : 3 1 8 4 3 7 2 15 : 3 15 2 (18 : 3) 2 5 12 : 6 1 4 3 3 (24 : 4) 2 3 1 8 3 Calcula la fracción de un número. 3 5 de 230 5 8 de 3.200 2 7 de 560 4 9 de 5.400 7 Para regalar a unos amigos, Marta compra un peluche por 8,90 €, una raqueta por 15,50 € y un balón por 6,80 €. ¿Cuánto gasta Marta en total? 8 En la tienda de Alberto hay 4 cajas con 6 lámparas cada una. Cada lámpara tiene 5 brazos y, en cada uno, hay 3 bombillas. ¿Cuántas bombillas en total tienen las lámparas? 9 Marcos paga una factura de 135,67 € con un billete de 100 € y otro de 50 €. ¿Cuánto dinero le sobra? ¿Cómo pueden dárselo usando el menor número de billetes y monedas posible? 10 En un teatro hay 25 filas con 15 butacas cada una y 12 filas con 8 butacas cada una. ¿Cuántas butacas en total tiene el teatro? 11 Miguel lleva en su furgoneta 15 cajas con 30 tarros de mermelada cada caja. El total lo reparte en partes iguales entre 4 supermercados. ¿Cuántos tarros de mermelada deja en cada uno? 12 En el pueblo de Natalia viven 25.000 personas. Un cuarto de las personas se dedica a la agricultura, tres quintos a la ganadería y el resto a la industria. ¿Cuántas personas se dedican a la industria? Problemas REPASO ACUMULATIVO 10 155 ES0000000024590 663006-Unidad 10_22593.indd 155 10/03/2015 13:21:50 UNIDAD 10 5 • R. M. 8 unidades y 9 décimas 8 coma 9 • 3 unidades y 78 centésimas • 4 unidades y 621 milésimas • 32 unidades y 5 décimas • 15 unidades y 3 centésimas • 7 unidades y 72 milésimas 6 • 160,26 • 123,378 • 22,01 • 44,8 • 421,638 • 2.750 7 8,90 1 15,50 1 6,80 5 31,20 Se gastó 31,20 €. 8 4 3 6 3 5 3 3 5 360 Tienen 360 bombillas. 9 150 2 135,67 5 14,33 € 1 billete de 10 €, 2 monedas de 2 €, 1 moneda de 0,20 €, 1 de 0,10 €, 1 de 0,02 € y otra de 0,01 €. 10 25 3 15 1 12 3 8 5 471 El teatro tiene 471 butacas. 11 15 3 30 5 450 450 : 4 c 5 112, r 5 2 Deja 112 tarros en cada supermercado y le quedan 2. 12 1 4 de 25.000 5 6.250 3 5 de 25.000 5 15.000 25.000 2 6.250 2 15.000 5 3.750 A la industria se dedican 3.750 personas. Notas Repaso en común • Después de que los alumnos realicen las actividades de esta página de manera individual o en pequeños grupos, pídales que expongan cuáles de ellas les han resultado más difíciles. Repase con ellos los conceptos o procedimientos implicados en esas actividades y corríjalas en común. Cada alumno o grupo, más tarde, planteará y realizará en una hoja aparte actividades similares a las dificultosas para reforzar la comprensión. 89
Javi, Ana y Luis han quedado para ir a volar sus cometas. 1 Observa las cometas de cada niño y escribe en tu cuaderno la fracción que representa la zona de cada color. 2 Escribe cómo se lee la fracción que representa la zona roja de cada cometa. 3 En cada cometa, ordena de menor a mayor las fracciones que representan las zonas de cada color. 4 Copia y completa la tabla en tu cuaderno. Después, escribe cómo se lee cada número. 5 Ordena los números y utiliza el signo adecuado. 12,9 9,5 21,75 54,9 54,84 45,765 9,542 9,524 9,521 5,865 7,65 9,6 21,83 21,38 24,9 5,782 5,872 5,827 12 1 2 3 4 567 8 9 10 11 Propósitos •  Repasar los contenidos clave del trimestre. Actividades 1 Javi: 4 9 rojo, 3 9 amarilla, 2 9 azul. Ana: 3 10 rojo, 2 10 amarilla,   5 10 azul. Luis: 3 8 rojo, 1 8 amarilla, 4 8 azul. 2 Cuatro novenos. Tres décimos. Tres octavos. 3 Javi: 2 9 , 3 9 , 4 9 Ana: 2 10 , 3 10 , 5 10 Luis: 1 8 , 3 8 , 4 8 4 • 4 U 1 8 d • 3 D 1 5 U 1 6 c • 9 U 1 3 d 1 1 c 1 5 m • 4 D 1 5 U 1 7 c 1 2 m • 1 D 1 8 U 1 8 m 5 • 9,5 , 12,9 , 21,75 • 45,765 , 54,84 , 54,9 • 9,521 , 9,524 , 9,542 • 9,6 . 7,65 . 5,865 • 24,9 . 21,83 . 21,38 • 5,872 . 5,827 . 5,782 6 • 43,66 • 818,65 • 66,797 • 147,29 • 357,95 • 60,936 • 55,76 • 25,5264 • 0,9048 • 78,9 • 580 • 1.900 7 Las 7 menos veinticinco de la tarde. Repaso trimestral Javi, Ana y Luis han quedado para ir a volar sus cometas. 1 Observa las cometas de cada niño y escribe en tu cuaderno la fracción que representa la zona de cada color. 2 Escribe cómo se lee la fracción que representa la zona roja de cada cometa. 3 En cada cometa, ordena de menor a mayor las fracciones que representan las zonas de cada color. 4 Copia y completa la tabla en tu cuaderno. Después, escribe cómo se lee cada número. 5 Ordena los números y utiliza el signo adecuado. 12,9 9,5 21,75 54,9 54,84 45,765 9,542 9,524 9,521 5,865 7,65 9,6 21,83 21,38 24,9 5,782 5,872 5,827 Javi Ana Luis De menor a mayor De mayor a menor JAVI ANALUIS Parte entera Parte decimal Decenas Unidades Décimas Centésimas Milésimas 4,8 35,06 9,315 45,072 18,008 156 ES0000000024590 663006-Repaso2_22594.indd 156 10/03/2015 13:21:15 90
SEGUNDO TRIMESTRE 12 1 2 3 4 567 8 9 10 11 12 1 2 3 4 567 8 9 10 1112 1 2 3 4 567 8 9 10 11 12 1 2 3 4 567 8 9 10 1112 1 2 3 4 567 8 9 10 11 6 Calcula. 34,9 1 8,76 754,9 1 63,75 9,845 1 56,952 231,89 2 84,6 432,9 2 74,95 70,5 2 9,564 32,8 3 1,7 5,318 3 4,8 6,032 3 0,15 7,89 3 10 5,8 3 100 1,9 3 1.000 7 Escribe la hora de cada reloj digital tal como se lee en un reloj de agujas. ¿Qué hora marcará cada reloj cuando hayan pasado 2 horas y 25 minutos? 8 Expresa en la unidad que se indica. 2 m, 5 dm y 7 cm 4 m, 6 dm y 9 cm 5 m y 8 dm 1 m, 2 cm y 9 mm 3 m y 7 mm 5 m, 7 dm y 8 cm 2 km, 3 hm y 4 dam 3 km, 5 hm y 6 m 6 km y 5 dam Problemas 9 Resuelve. Para envolver regalos, Lucía tiene un rollo de cinta de 3,5 m. Primero cortó 0,75 m y después cortó 1,55 m. ¿Cuántos metros de cinta le quedan en el rollo? Arturo compra 3 CD de música a 8,95 € cada uno y un libro por 14,50 €. Para pagar entrega un billete de 50 €. ¿Cuánto dinero le devuelven? Nuria tiene en su puesto 350 helados. Hoy ha vendido dos quintos de los helados a 1,50 € cada uno. ¿Cuánto ha recaudado Nuria por esta venta? Todos los días, un tren sale de la estación a las 9 menos cuarto de la mañana y tarda 3 horas y media en llegar a su destino. Hoy el tren ha salido con 25 minutos de retraso y ha tardado 4 horas y cuarto en llegar a su destino. ¿A qué hora ha salido de la estación? ¿A qué hora ha llegado a su destino? Representa las horas en un reloj de agujas y en un reloj digital. 18:35 13:40 22:50 157 En centímetros En milímetros En metros ES0000000024590 663006-Repaso2_22594.indd 157 10/03/2015 13:21:17 Las 2 menos veinte de la tarde. Las 11 menos diez de la noche. • Las 9 de la noche. Las 4 y cinco de la tarde. La 1 y cuarto de la mañana. 8 • 257 cm • 469 cm • 580 cm • 1.029 mm • 3.007 mm •  5.780 • 2.340 m • 3.506 m • 6.050 m 9 • 3,5 2 0,75 2 1,55 5 1,2 Le quedan 1,2 m. • 3 3 8,95 1 14,50 5 41,35 50 2 41,35 5 8,65 Le devuelven 8,65 €. • 2/5 de 350 5 140 140 3 1,50 5 210 Ha recaudado 210 €. • 8:45 1 25 5 9:10 Ha salido a las 9 y diez. 9:10 1 4:15 = 13:25 Ha llegado a la 1 y veinticinco de la tarde. Compruebe que los alumnos representan las horas correctamente. Notas 91
Notas
Notas
Notas
Notas
Libro Matematicas 2ºEV 4ºPrimaria

Más contenido relacionado

PDF
Fracciones decimales porcentajes tema 7
pormayka18
 
PDF
Problemas de matematicas decimales y fracciones 6º de primaria
porEdubecerra
 
PDF
Matematica 5° tomo I casa del saber
porLucia Cortes
 
PDF
5to Matematicas - SANTILLANA.pdf
porRnaldCaldern
 
PPTX
Convertir fracciones en números decimaes y viceversa
porkizzyariassilva
 
PDF
Me preparo para 3º de Primaria
porCSJ-1-2
 
DOC
Criterios de divisibilidad
porSilvia Nuñez
 
PDF
Actividades de áreas
porFernando Martinez
 
Fracciones decimales porcentajes tema 7
pormayka18
 
Problemas de matematicas decimales y fracciones 6º de primaria
porEdubecerra
 
Matematica 5° tomo I casa del saber
porLucia Cortes
 
5to Matematicas - SANTILLANA.pdf
porRnaldCaldern
 
Convertir fracciones en números decimaes y viceversa
porkizzyariassilva
 
Me preparo para 3º de Primaria
porCSJ-1-2
 
Criterios de divisibilidad
porSilvia Nuñez
 
Actividades de áreas
porFernando Martinez
 

La actualidad más candente

PPTX
Convertir decimales a fracciones
porleonelalbertoneri
 
DOCX
Control valor posicional
porMiguel Diaz
 
PDF
Cambio y variacion ii
pormonica botiva
 
PDF
Refuerzo y ampliacion matematicas tercero
porpilarcale
 
PPTX
Proyecto democracia SANMIGAR
porMyriam Hernandez Mogollon
 
PPT
Numeros de seis cifras
porJOHNDOMINGUEZPICO
 
DOCX
DÉCIMO, CENTÉSIMO Y MILÉSIMO.docx
porVeronica Cespedes
 
PDF
ONE 2013: Criterios de evaluación. Matemática.
porPedro Roberto Casanova
 
PDF
Práctica con plano cartesiano
porsahyli77
 
PDF
Los numeros-romanos-para-cuarto-de-primaria
pordayanavelasquez18
 
DOCX
Rúbrica de evaluación pproceso fracciones
porClaudia Oliva
 
DOCX
PLANTEO DE ECUACIONES - 1 - PRIMARIA
porFlorencio Huaypuna
 
PDF
Fracciones decimales
porNiris Ofelia Moreno Cañadas
 
DOCX
Valor posicional para sexto grado
porSecretaría de Educación de Veracruz
 
PPTX
Múltiplos y submúltiplos
porFernando Martinez
 
ODP
Numeros decimales
pormayka18
 
DOCX
Actividad Flora y Fauna
porFallown Espinace
 
PDF
cuaderno santillana 4°.pdf
porVicenteMuoz53
 
DOCX
Prueba recursos naturales
porPao Cárdenas
 
PDF
La carta
porlina marcela franco osorio
 
Convertir decimales a fracciones
porleonelalbertoneri
 
Control valor posicional
porMiguel Diaz
 
Cambio y variacion ii
pormonica botiva
 
Refuerzo y ampliacion matematicas tercero
porpilarcale
 
Proyecto democracia SANMIGAR
porMyriam Hernandez Mogollon
 
Numeros de seis cifras
porJOHNDOMINGUEZPICO
 
DÉCIMO, CENTÉSIMO Y MILÉSIMO.docx
porVeronica Cespedes
 
ONE 2013: Criterios de evaluación. Matemática.
porPedro Roberto Casanova
 
Práctica con plano cartesiano
porsahyli77
 
Los numeros-romanos-para-cuarto-de-primaria
pordayanavelasquez18
 
Rúbrica de evaluación pproceso fracciones
porClaudia Oliva
 
PLANTEO DE ECUACIONES - 1 - PRIMARIA
porFlorencio Huaypuna
 
Fracciones decimales
porNiris Ofelia Moreno Cañadas
 
Valor posicional para sexto grado
porSecretaría de Educación de Veracruz
 
Múltiplos y submúltiplos
porFernando Martinez
 
Numeros decimales
pormayka18
 
Actividad Flora y Fauna
porFallown Espinace
 
cuaderno santillana 4°.pdf
porVicenteMuoz53
 
Prueba recursos naturales
porPao Cárdenas
 
La carta
porlina marcela franco osorio
 

Similar a Libro Matematicas 2ºEV 4ºPrimaria

PDF
Libro Matematicas 3ºEV 4ºPrimaria
porDiegoFernndezVillar
 
PDF
292322_Libro_anotado_Matematicas_4Prim_CM_cast.pdf
porAna Garcia
 
PDF
TIC unidad didáctica matemáticas.pdf
porGrupo177
 
PDF
matemáticas 5to primariaEl libro Matemáticas 5, para quinto curso de Educació...
porGastonMartinCadilloL
 
DOC
Plan 5to grado - bloque iv - matemáticas
porChelk2010
 
PDF
control y evaluacion-lengua 3.pdf
porMTeresaRius2
 
PDF
MATE MAS.pdf
pormarthalargo
 
PDF
PLANIFICACION ANUAL MATEMATICA CUARTO.pdf
porlauralorenaVerdun1
 
PDF
Reforzamiento y practica de destrezas 3
porLuis Hernández
 
DOC
Plan 4to grado bloque iv - matemáticas
porChelk2010
 
PDF
842811.pdf
porCesarHernandez17550
 
PPTX
Sec. dca. temática matemätica 1er trimestre
porphontakly
 
DOC
Nb2 cuarto basico
porMarcos Spröhnle
 
DOC
Plan anual 2014 4 to básico
porMarcos Spröhnle
 
PPTX
3er t sec. dca. temática matemätica 3er trimestre
porlibre
 
DOCX
indice-7709228857740.docx
porISABELARANGO17
 
PDF
Matemáticas 6º libro.pdf
porCristinaS46
 
DOCX
Programación edelvives 5mates
porBelen Garcia
 
DOCX
Guía de matemáticas primero bloque 1- ejercicios
porJEDANNIE Apellidos
 
PDF
Matematicas 6º Primaría
porEsteban Cruz
 
Libro Matematicas 3ºEV 4ºPrimaria
porDiegoFernndezVillar
 
292322_Libro_anotado_Matematicas_4Prim_CM_cast.pdf
porAna Garcia
 
TIC unidad didáctica matemáticas.pdf
porGrupo177
 
matemáticas 5to primariaEl libro Matemáticas 5, para quinto curso de Educació...
porGastonMartinCadilloL
 
Plan 5to grado - bloque iv - matemáticas
porChelk2010
 
control y evaluacion-lengua 3.pdf
porMTeresaRius2
 
MATE MAS.pdf
pormarthalargo
 
PLANIFICACION ANUAL MATEMATICA CUARTO.pdf
porlauralorenaVerdun1
 
Reforzamiento y practica de destrezas 3
porLuis Hernández
 
Plan 4to grado bloque iv - matemáticas
porChelk2010
 
842811.pdf
porCesarHernandez17550
 
Sec. dca. temática matemätica 1er trimestre
porphontakly
 
Nb2 cuarto basico
porMarcos Spröhnle
 
Plan anual 2014 4 to básico
porMarcos Spröhnle
 
3er t sec. dca. temática matemätica 3er trimestre
porlibre
 
indice-7709228857740.docx
porISABELARANGO17
 
Matemáticas 6º libro.pdf
porCristinaS46
 
Programación edelvives 5mates
porBelen Garcia
 
Guía de matemáticas primero bloque 1- ejercicios
porJEDANNIE Apellidos
 
Matematicas 6º Primaría
porEsteban Cruz
 

Más de DiegoFernndezVillar

PDF
Tea stilton princesa de la oscuridad
porDiegoFernndezVillar
 
PDF
Nanopdf.com manolito on-the-road
porDiegoFernndezVillar
 
PDF
Mi nombre es stilton, geronimo stilton ( pdf drive.com )
porDiegoFernndezVillar
 
PDF
En busca de la maravilla perdid geronimo stilton
porDiegoFernndezVillar
 
PDF
El diario de greg
porDiegoFernndezVillar
 
PDF
Diario de greg vieja escuela ( pdf drive.com )
porDiegoFernndezVillar
 
PDF
Diario de greg la ley de rodrick ( pdf drive )
porDiegoFernndezVillar
 
PDF
Diario de greg dia de perros ( pdf drive.com )
porDiegoFernndezVillar
 
PDF
Diario de greg carretera y manta ( pdf drive.com )
porDiegoFernndezVillar
 
PDF
1er cap 9788408105114
porDiegoFernndezVillar
 
PDF
1er cap 9788408105220
porDiegoFernndezVillar
 
PDF
Libro Matematicas 1ºEV 4ºPrimaria
porDiegoFernndezVillar
 
Tea stilton princesa de la oscuridad
porDiegoFernndezVillar
 
Nanopdf.com manolito on-the-road
porDiegoFernndezVillar
 
Mi nombre es stilton, geronimo stilton ( pdf drive.com )
porDiegoFernndezVillar
 
En busca de la maravilla perdid geronimo stilton
porDiegoFernndezVillar
 
El diario de greg
porDiegoFernndezVillar
 
Diario de greg vieja escuela ( pdf drive.com )
porDiegoFernndezVillar
 
Diario de greg la ley de rodrick ( pdf drive )
porDiegoFernndezVillar
 
Diario de greg dia de perros ( pdf drive.com )
porDiegoFernndezVillar
 
Diario de greg carretera y manta ( pdf drive.com )
porDiegoFernndezVillar
 
1er cap 9788408105114
porDiegoFernndezVillar
 
1er cap 9788408105220
porDiegoFernndezVillar
 
Libro Matematicas 1ºEV 4ºPrimaria
porDiegoFernndezVillar
 

Último

PDF
Evaluación Educativa. José Francisco Lukas Mujika Ccesa007.pdf
porDemetrio Ccesa Rayme
 
PDF
AGRA4305-PracticasSupervisadas/Dept_de_Disenyo
porAlberto Soto
 
PPTX
TALLER INTEGRAL VI. Elaboración (DTT) para Titulación
porEstudiosendiseoAM
 
PDF
Fundamentos de Algebra Lineal - Ron Larson Ccesa007.pdf
porDemetrio Ccesa Rayme
 
PDF
Serie Inteligencia Emocional. Cómo crear un Plan de Negocio HBR Ccesa007.pdf
porDemetrio Ccesa Rayme
 
PPTX
102.Repaso 4 lugares:ir.ppt. x
porbrianjars
 
PDF
La Planificacion Didactica GRAO Ccesa007.pdf
porDemetrio Ccesa Rayme
 
PDF
El Camino Hacia la Riqueza – Brian Tracy Ccesa007.pdf
porDemetrio Ccesa Rayme
 
PPTX
SPAN 102 - Repaso para la prueba 1.ppt. x
porbrianjars
 
PDF
Serie Inteligencia Emocional. Energia Y Motivación HBR Ccesa007.pdf
porDemetrio Ccesa Rayme
 
PDF
Presidenta del CNE, Ana Paola Hall, agradece apoyo y revela embajada donde se...
porpegazohn1978
 
PDF
La Riqueza que el dinero no puede comprar - Robin Sharma Ccesa007.pdf
porDemetrio Ccesa Rayme
 
PDF
Física Universitaria - Francis Sears, Mark Zemansky Ccesa007.pdf
porDemetrio Ccesa Rayme
 
PDF
Desarrollo de Hablidades Directivas Ccesa007.pdf
porDemetrio Ccesa Rayme
 
PDF
MONOGRAFIA. CURRÍCULUM.LYA-2.pdftrabajofinal
porantoniomiguel2011201
 
PDF
Esc. Sab. Lec. 4. Unidad mediante la humildad.pdf
porAlejandrino Halire Ccahuana
 
PDF
Inteligencia Social. La Nueva Ciencia de las Relaciones Humanas Ccesa007.pdf
porDemetrio Ccesa Rayme
 
PDF
Seminario "La IA, entre alucinaciones y aciertos: marco de trabajo para tarea...
porUniversidad Internacional de Andalucía
 
PDF
Feng Shui y el Poder de la Piramide Ccesa007.pdf
porDemetrio Ccesa Rayme
 
PDF
Acoso Escolar. Redes Sociales - Emilio Tresgallo Ccesa007.pdf
porDemetrio Ccesa Rayme
 
Evaluación Educativa. José Francisco Lukas Mujika Ccesa007.pdf
porDemetrio Ccesa Rayme
 
AGRA4305-PracticasSupervisadas/Dept_de_Disenyo
porAlberto Soto
 
TALLER INTEGRAL VI. Elaboración (DTT) para Titulación
porEstudiosendiseoAM
 
Fundamentos de Algebra Lineal - Ron Larson Ccesa007.pdf
porDemetrio Ccesa Rayme
 
Serie Inteligencia Emocional. Cómo crear un Plan de Negocio HBR Ccesa007.pdf
porDemetrio Ccesa Rayme
 
102.Repaso 4 lugares:ir.ppt. x
porbrianjars
 
La Planificacion Didactica GRAO Ccesa007.pdf
porDemetrio Ccesa Rayme
 
El Camino Hacia la Riqueza – Brian Tracy Ccesa007.pdf
porDemetrio Ccesa Rayme
 
SPAN 102 - Repaso para la prueba 1.ppt. x
porbrianjars
 
Serie Inteligencia Emocional. Energia Y Motivación HBR Ccesa007.pdf
porDemetrio Ccesa Rayme
 
Presidenta del CNE, Ana Paola Hall, agradece apoyo y revela embajada donde se...
porpegazohn1978
 
La Riqueza que el dinero no puede comprar - Robin Sharma Ccesa007.pdf
porDemetrio Ccesa Rayme
 
Física Universitaria - Francis Sears, Mark Zemansky Ccesa007.pdf
porDemetrio Ccesa Rayme
 
Desarrollo de Hablidades Directivas Ccesa007.pdf
porDemetrio Ccesa Rayme
 
MONOGRAFIA. CURRÍCULUM.LYA-2.pdftrabajofinal
porantoniomiguel2011201
 
Esc. Sab. Lec. 4. Unidad mediante la humildad.pdf
porAlejandrino Halire Ccahuana
 
Inteligencia Social. La Nueva Ciencia de las Relaciones Humanas Ccesa007.pdf
porDemetrio Ccesa Rayme
 
Seminario "La IA, entre alucinaciones y aciertos: marco de trabajo para tarea...
porUniversidad Internacional de Andalucía
 
Feng Shui y el Poder de la Piramide Ccesa007.pdf
porDemetrio Ccesa Rayme
 
Acoso Escolar. Redes Sociales - Emilio Tresgallo Ccesa007.pdf
porDemetrio Ccesa Rayme
 

Libro Matematicas 2ºEV 4ºPrimaria

  • 1.
    PRIMARIA Matemáticas GUÍA DIDÁCTICA BIBLIOTECA DELPROFESORADO La guía didáctica Matemáticas 4, para cuarto curso de Primaria, es una obra colectiva concebida, diseñada y creada en el Departamento de Ediciones Educativas de Santillana Educación, S. L., dirigido por Teresa Grence Ruiz. En su elaboración ha participado el siguiente equipo: TEXTO Y EDICIÓN José Antonio Almodóvar Herráiz Pilar García Atance ILUSTRACIÓN Irene Hervás Alonso Felipe López Salán Eduardo Leal Uguina EDICIÓN EJECUTIVA José Antonio Almodóvar Herráiz DIRECCIÓN DEL PROYECTO Domingo Sánchez Figueroa DIRECCIÓN Y COORDINACIÓN EDITORIAL DE PRIMARIA Maite López-Sáez Rodríguez-Piñero
  • 2.
    Dirección de arte:José Crespo Proyecto gráfico: Estudio Pep Carrió Fotografía de la cubierta: Leila Méndez Jefa de proyecto: Rosa Marín Coordinación de ilustración: Carlos Aguilera Jefe de desarrollo de proyecto: Javier Tejeda Desarrollo gráfico: Jorge Gómez, Raúl de Andrés Dirección técnica: Jorge Mira Subdirección técnica: José Luis Verdasco Coordinación técnica: Alejandro Retana Confección y montaje: Hilario Simón, Raquel Sánchez Corrección: Marta Rubio, Nuria del Peso Documentación y selección fotográfica: Nieves Marinas Fotografías: J. Jaime; A. G. E. FOTOSTOCK/Fernando Fernández; GETTY IMAGES SALES SPAIN/Photos.com Plus; HIGHRES PRESS STOCK/AbleStock.com; STOCKBYTE; MATTON-BILD; SERIDEC PHOTOIMAGENES CD; ARCHIVO SANTILLANA Cualquier forma de reproducción, distribución, comunicación pública o transformación de esta obra solo puede ser realizada con la autorización de sus titulares, salvo excepción prevista por la ley. Diríjase a CEDRO (Centro Es- pañol de Derechos Reprográficos, www.cedro.org <http://www.cedro.org>) si necesita fotocopiar o escanear algún fragmento de esta obra. © 2015 by Santillana Educación, S. L. Avda. de los Artesanos, 6 28760 Tres Cantos, Madrid PRINTED IN SPAIN ISBN: 978-84-8305-567-0 CP: 664734 Depósito legal: M-24540-2015
  • 3.
    Índice Mapa de contenidos................................................... 4 Guiones didácticos Unidad 6. Fracciones..................................................  6 Unidad 7. Números decimales.................................... 24 Unidad 8. Operaciones con números decimales........ 40 Unidad 9. Tiempo y dinero.......................................... 58 Unidad 10. Longitud.................................................... 74
  • 4.
    Unidades Información yactividades 1 Números de hasta siete cifras 6 • Números de seis cifras • Aproximaciones • Números de siete cifras • Números romanos 2 Suma y resta 22 • Propiedades conmutativa y asociativa • Sumas y restas combinadas • Estimación de sumas y de restas 3 Multiplicación 36 • Multiplicación por números de varias cifras • Estimación de productos • Propiedades de la multiplicación Tratamiento de la información. Coordenadas de puntos en una cuadrícula 4 División 52 • División exacta y división entera • Divisiones con ceros en el cociente • Prueba de la división • Operaciones combinadas 5 Práctica de la división 66 • Divisiones con divisor de dos cifras (I) • Propiedad de la división exacta • Divisiones con divisor de dos cifras (II) REPASO TRIMESTRAL 6 Fracciones 82 • Fracciones. Comparación de fracciones • Fracciones propias e impropias • Fracción de un número • Números mixtos 7 Números decimales 98 • Unidades decimales • Comparación de decimales • Números decimales • Aproximación de decimales 8 Operaciones con números decimales 112 • Suma de números decimales • Multiplicación de números • Resta de números decimales decimales Tratamiento de la información. de barras de tres características 9 Tiempo y dinero 128 • El reloj digital • Problemas con tiempo y dinero • Unidades de tiempo 10 Longitud 142 • El metro, el decímetro y el centímetro • El kilómetro, el hectómetro • El milímetro y el decámetro REPASO TRIMESTRAL 11 Capacidad y masa 158 • El decilitro, el centilitro y el mililitro • El decagramo, el hectogramo • El decalitro, el hectolitro y el kilolitro y el kilogramo • El decigramo, el centigramo • Problemas de medida y el miligramo 12 Rectas y ángulos 172 • Recta, semirrecta y segmento • Simetrías y traslaciones • Medida y trazado de ángulos 13 Polígonos 186 • Perímetro. Polígonos regulares • de triángulos • de cuadriláteros y paralelogramos Tratamiento de la información. Pictogramas 14 Cuerpos geométricos 202 • Prismas y pirámides. Elementos • Cuerpos redondos • de prismas y pirámides 15 Probabilidad y estadística 216 • Suceso seguro, posible e imposible • Media • Más probable y menos probable REPASO TRIMESTRAL Unidades Información y actividades 1 Números de hasta siete cifras 6 • Números de seis cifras • Aproximaciones • Números de siete cifras • Números romanos 2 Suma y resta 22 • Propiedades conmutativa y asociativa • Sumas y restas combinadas • Estimación de sumas y de restas 3 Multiplicación 36 • Multiplicación por números de varias cifras • Estimación de productos • Propiedades de la multiplicación Tratamiento de la información. Coordenadas de puntos en una cuadrícula 4 División 52 • División exacta y división entera • Divisiones con ceros en el cociente • Prueba de la división • Operaciones combinadas 5 Práctica de la división 66 • Divisiones con divisor de dos cifras (I) • Propiedad de la división exacta • Divisiones con divisor de dos cifras (II) REPASO TRIMESTRAL 6 Fracciones 82 • Fracciones. Comparación de fracciones • Fracciones propias e impropias • Fracción de un número • Números mixtos 7 Números decimales 98 • Unidades decimales • Comparación de decimales • Números decimales • Aproximación de decimales 8 Operaciones con números decimales 112 • Suma de números decimales • Multiplicación de números • Resta de números decimales decimales Tratamiento de la información. de barras de tres características 9 Tiempo y dinero 128 • El reloj digital • Problemas con tiempo y dinero • Unidades de tiempo 10 Longitud 142 • El metro, el decímetro y el centímetro • El kilómetro, el hectómetro • El milímetro y el decámetro REPASO TRIMESTRAL 11 Capacidad y masa 158 • El decilitro, el centilitro y el mililitro • El decagramo, el hectogramo • El decalitro, el hectolitro y el kilolitro y el kilogramo • El decigramo, el centigramo • Problemas de medida y el miligramo 12 Rectas y ángulos 172 • Recta, semirrecta y segmento • Simetrías y traslaciones • Medida y trazado de ángulos 13 Polígonos 186 • Perímetro. Polígonos regulares • de triángulos • de cuadriláteros y paralelogramos Tratamiento de la información. Pictogramas 14 Cuerpos geométricos 202 • Prismas y pirámides. Elementos • Cuerpos redondos • de prismas y pirámides 15 Probabilidad y estadística 216 • Suceso seguro, posible e imposible • Media • Más probable y menos probable REPASO TRIMESTRAL
  • 5.
    Cálculo mental Soluciónde problemas Saber hacer • Sumar decenas, centenas y millares • Restar decenas, centenas y millares • Pasos para resolver un problema • Analizar datos de estadios • Sumar decenas a números de 3 y de 4 cifras • Restar decenas a números de 3 y de 4 cifras • Completar enunciados • Elegir regalos con puntos • Sumar centenas a números de 3 y de 4 cifras • Restar centenas a números de 3 y de 4 cifras • Reconstruir el enunciado • Comprobar un pedido • Multiplicar un número por 10, 100 y 1.000 • Multiplicar un dígito por decenas, centenas y millares • Sacar conclusiones de un enunciado • Conocer las reglas de un juego • Multiplicar dos números terminados en cero • Multiplicar números de 2 cifras por 2 y por 20 • Averiguar los datos que sobran e inventar preguntas • Organizar grupos • Dividir decenas, centenas y millares entre 10 • Dividir centenas y millares entre 100 y entre 1.000 • Averiguar e inventar los datos que faltan • Comprender noticias con fracciones • Hallar la mitad de decenas y de centenas • Hallar la mitad de números de 2 y de 3 cifras • Ordenar los datos de un problema • Estudiar la evolución de un precio • Sumar 11 a un número • Sumar 9 a un número • Extraer datos de la resolución de un problema • Revisar una factura • Restar 11 a un número • Restar 9 a un número • Cambiar datos para obtener una solución distinta • Programar horarios • Sumar números de 2 cifras sin llevar • Sumar números de 2 cifras llevando • Elegir la pregunta para que el problema se resuelva con dos operaciones • Interpretar datos de altitudes • Sumar 21, 31, 41... a números de 2 cifras • Sumar 19, 29, 39... a números de 2 cifras • Elegir la pregunta que se responde con unos cálculos • Realizar cálculos en un laboratorio • Restar 21, 31, 41... a números de 2 cifras • Restar 19, 29, 39... a números de 2 cifras • Elegir las preguntas que se pueden responder a partir del enunciado • Trabajar con ángulos en los deportes • Sumar 101, 201... a números de 3 cifras • Sumar 99, 199... a números de 3 cifras • Escribir las cuestiones intermedias en problemas de dos o más operaciones • Analizar mosaicos • Multiplicar por 11 números de 2 cifras • Multiplicar por 101 números de 2 cifras • Elegir los cálculos que resuelven un problema • Interpretar una maqueta • Multiplicar por 5 números de 2 cifras • Multiplicar por 50 números de 2 cifras • Elegir la solución más razonable • Elegir la estrategia en un concurso Cálculo mental Solución de problemas Saber hacer • Sumar decenas, centenas y millares • Restar decenas, centenas y millares • Pasos para resolver un problema • Analizar datos de estadios • Sumar decenas a números de 3 y de 4 cifras • Restar decenas a números de 3 y de 4 cifras • Completar enunciados • Elegir regalos con puntos • Sumar centenas a números de 3 y de 4 cifras • Restar centenas a números de 3 y de 4 cifras • Reconstruir el enunciado • Comprobar un pedido • Multiplicar un número por 10, 100 y 1.000 • Multiplicar un dígito por decenas, centenas y millares • Sacar conclusiones de un enunciado • Conocer las reglas de un juego • Multiplicar dos números terminados en cero • Multiplicar números de 2 cifras por 2 y por 20 • Averiguar los datos que sobran e inventar preguntas • Organizar grupos • Dividir decenas, centenas y millares entre 10 • Dividir centenas y millares entre 100 y entre 1.000 • Averiguar e inventar los datos que faltan • Comprender noticias con fracciones • Hallar la mitad de decenas y de centenas • Hallar la mitad de números de 2 y de 3 cifras • Ordenar los datos de un problema • Estudiar la evolución de un precio • Sumar 11 a un número • Sumar 9 a un número • Extraer datos de la resolución de un problema • Revisar una factura • Restar 11 a un número • Restar 9 a un número • Cambiar datos para obtener una solución distinta • Programar horarios • Sumar números de 2 cifras sin llevar • Sumar números de 2 cifras llevando • Elegir la pregunta para que el problema se resuelva con dos operaciones • Interpretar datos de altitudes • Sumar 21, 31, 41... a números de 2 cifras • Sumar 19, 29, 39... a números de 2 cifras • Elegir la pregunta que se responde con unos cálculos • Realizar cálculos en un laboratorio • Restar 21, 31, 41... a números de 2 cifras • Restar 19, 29, 39... a números de 2 cifras • Elegir las preguntas que se pueden responder a partir del enunciado • Trabajar con ángulos en los deportes • Sumar 101, 201... a números de 3 cifras • Sumar 99, 199... a números de 3 cifras • Escribir las cuestiones intermedias en problemas de dos o más operaciones • Analizar mosaicos • Multiplicar por 11 números de 2 cifras • Multiplicar por 101 números de 2 cifras • Elegir los cálculos que resuelven un problema • Interpretar una maqueta • Multiplicar por 5 números de 2 cifras • Multiplicar por 50 números de 2 cifras • Elegir la solución más razonable • Elegir la estrategia en un concurso
  • 6.
    Fracciones6 Contenidos de launidad SABER NÚMEROS Y OPERACIONES • Fracciones. • Comparación de fracciones. • Fracción de un número. • Fracciones propias e impropias. • Números mixtos. SABER HACER NÚMEROS Y OPERACIONES • Lectura, escritura, representación e interpretación de fracciones. • Comparación de fracciones con igual numerador o con igual denominador. • Cálculo de la fracción de un número. • Reconocimiento de fracciones propias e impropias. • Comparación de fracciones y números naturales. • Reconocimiento de números mixtos. • Representación de números mixtos. • Resolución de problemas utilizando fracciones, comparación de fracciones y cálculo de la fracción de un número. RESOLUCIÓN DE PROBLEMAS • Resolución de problemas inventando los datos que faltan. • Invención de problemas que se resuelvan a partir de unos cálculos dados que hay que completar.   TAREA FINAL • Comprender noticias con fracciones. SABER SER FORMACIÓN EN VALORES • Valoración de la utilidad de las fracciones para resolver diversas situaciones reales. • Interés por la resolución de problemas. 6
  • 7.
    BIBLIOTECA DEL PROFESORADO Programacióndidáctica de aula Recursos para la evaluación • Evaluación de contenidos. Unidad 6: pruebas de control B y A. • Evaluación por competencias. Prueba 6. •  Rúbrica. Unidad 6. Enseñanza individualizada • Plan de mejora. Unidad 6. • Programa de ampliación. Unidad 6. Proyectos de trabajo cooperativo • Proyecto del segundo trimestre. Recursos complementarios • Fichas para el desarrollo de la inteligencia. • Operaciones y problemas. Aprendizaje eficaz • Técnicas de estudio y presentación de exámenes. Proyectos interdisciplinares • Programa de Educación en valores. • Programa de Educación emocional. •  Inteligencias múltiples. RECURSOS DIGITALES LibroMedia • Unidad 6: actividades y recursos. MATERIAL DE AULA Láminas OTROS MATERIALES DEL PROYECTO Cuaderno del alumno • Segundo trimestre. Unidad 6. Solución de problemas. Método DECA ES0000000024590 663006_Matematicas_4_GRAZ_24259 PRIMARIA PRIMARIA Matemáticas PRIMARIA ANDALUCÍAMatemáticas ANDALUCÍA Matemáticas ANDALUCÍA ES0000 000024 590 663006 _Matem aticas_4_GRA Z_2425 9.indd 1 04/03/2 015 11:21:19 ES0000000024593 663039_Cdno_Matematicas_4-2_22732 PRIMARIA Matemáticas Segundo trimestre Matemáticas Segundo trimestre PRIMARIA CUADERNO CUADERNO ES0000000024593 663039_Cdno_Matematicas_4-2_22732.indd 1 19/02/2015 16:56:18 SUGERENCIA DE TEMPORALIZACIÓN Enero MarzoFebrero 7
  • 8.
    6 Fracciones Limpiando elbosque Otro año más, los vecinos de Villares se reúnen para ir a los montes cercanos y limpiarlos. Personas de todas las edades colaboran ese día. Entre los pequeños esta iniciativa es cada vez más popular y cada año se apuntan más. En muy poco tiempo se limpia todo el monte y se deja preparado para poder disfrutarlo. Limpiadores por edades cada año Niños Adultos Mayores 2013 2014 82 ES0000000024590 663006-Unidad 06_22589.indd 82 10/03/2015 13:16:43 Limpiadores por edades cada año Niños Adultos Mayores 2013 2014 Propósitos •  Reconocer situaciones reales   en las que para su resolución   se utilizan las fracciones. •  Recordar los conceptos básicos necesarios para el desarrollo   de la unidad. Previsión de dificultades •  Aunque los alumnos resuelvan bien las actividades, pueden hacerlo   de forma mecánica, sin comprender el concepto de fracción. Pregúnteles a menudo qué significa cada término de la fracción. •  Puede resultarles complejo   el calcular la fracción de un número y aplicarlo en la resolución de problemas. Trabaje el proceso   de forma colectiva, pidiendo a los alumnos que expliquen los pasos realizados. •  Para evitar errores de comprensión con los números mixtos muestre siempre su equivalencia con la suma de cierto número de unidades completas y una fracción propia. Trabajo colectivo sobre la lámina Lea la lectura y pregunte a los alumnos su opinión acerca de   la limpieza de los bosques, por qué creen que es importante limpiarlos, etc. A continuación pídales que observen el gráfico y realice de forma colectiva la primera cuestión para comprobar que los alumnos   lo interpretan correctamente. 1   El gráfico de 2013 tiene 5 partes.   Una parte corresponde a los niños, dos a los adultos   y una a los mayores. 2   En 2014 los niños fueron dos partes.  Hubo más niños que en 2013,   ya que 2 1. Otras formas de empezar •  Lleve a la clase algunas piezas de fruta, por ejemplo, una manzana, una pera, un melocotón, una mandarina, etc. Divida, a la vista de los alumnos, cada pieza de fruta en varios trozos iguales o la mandarina en gajos. Por turno, los alumnos elegirán una fruta, cogerán algunos de sus trozos   y le dirán cuántos trozos (o gajos) hay de esa fruta y cuántos han cogido, siguiendo este modelo: «Hay … trozos de … y he cogido … trozos».   Pídales después que escriban la fracción asociada en la pizarra. 8
  • 9.
    ¿Qué sabes ya? 1El gráfico de 2013, ¿cuántas partes tiene? ¿Cuántas corresponden a los niños? ¿Cuántas partes corresponden a los adultos? ¿Y cuántas a los mayores? 2 ¿Qué parte de los limpiadores fueron niños en 2014? ¿Hubo mayor o menor número de niños limpiadores que en 2013? ¿Por qué? 3 EXPRESIÓN ORAL. Explica si el número de limpiadores adultos aumentó o disminuyó de 2013 a 2014. Lee, comprende y razona TAREA FINAL Comprender noticias con fracciones Entenderás noticias con fracciones. Antes, aprenderás a interpretarlas, escribirlas y compararlas, y a calcular la fracción de un número. SABER HACER La mitad de un número Para calcular la mitad de un número, divide ese número entre 2. La mitad de 16 16 : 2 5 8 La mitad de 40 40 : 2 5 20 La mitad de una figura Cada figura está dividida en dos partes iguales. La mitad de cada figura es de color rojo. 1 Calcula la mitad de cada número. 8 16 42 180 642 2.364 2 Escribe en tu cuaderno en qué figuras se ha coloreado la mitad. a. b. c. d. 83 ES0000000024590 663006-Unidad 06_22589.indd 83 10/03/2015 13:16:44 UNIDAD 6 3 En 2014 los adultos fueron dos partes del total de limpiadores, mientras que en 2013 fueron tres partes. El número de adultos disminuyó. ¿Qué sabes ya? Recuerde con los alumnos el procedimiento para calcular la mitad de un número y también el concepto de mitad de una figura geométrica. Señale que, para determinar la mitad en este último caso, hay que analizar si todas las partes son iguales, contar el número total de ellas y cuántas están coloreadas. 1 •  4 •  8 •  21 •  90 •  321 •  1.182 2 Figuras a, c y d. Notas Competencias •  Comunicación lingüística. Al realizar las actividades propuestas después de la lectura, es importante que los alumnos utilicen correctamente el lenguaje matemático para expresarse. Compruebe, sobre todo, en la de Expresión oral que lo hacen de forma clara. •  Aprender a aprender. Señale a los alumnos la importancia de afianzar los conocimientos para poder avanzar. Recuérdeles que ya en el curso pasado estudiaron las fracciones y el significado de sus términos, e indique que van a seguir aprendiendo más cosas sobre ellas. Inteligencia lingüística 9
  • 10.
    Fracciones: lectura yescritura 1 Copia las figuras y escribe la fracción que representa la parte coloreada. 2 Copia las figuras y colorea en cada una la fracción que se indica. 3 Copia la figura y colorea. Observa la parte de la figura que ha coloreado cada niño. Esta figura está dividida en 2 partes iguales. Hay 1 parte coloreada. Para expresarlo utilizamos esta fracción: 1 2 . Numerador. Número de partes coloreadas Denominador. Número de partes iguales de la figura Esta figura está dividida en 3 partes iguales. Hay 1 parte coloreada. Para expresarlo utilizamos esta fracción: 1 3 . Numerador. Número de partes coloreadas Denominador. Número de partes iguales de la figura 1 3 1 2 1 3 1 2 2 4 3 5 2 9 4 9 3 9 84 ES0000000024590 663006-Unidad 06_22589.indd 84 10/03/2015 13:16:46 Propósitos •  Leer y escribir fracciones. •  Reconocer los términos   de una fracción. •  Resolver problemas con fracciones. Sugerencias didácticas Para explicar. Lea la situación y,   con el apoyo de la ilustración, indique cómo se escribe la fracción correspondiente a cada figura   coloreada y el significado de cada término. Después, exprese cómo   se lee esta fracción y explique,   con la ayuda del cuadro del apartado Hazlo así, cómo se leen las fracciones cuyo denominador es un número menor o igual que 10. Deje claro que para poder hablar de fracciones debe cumplirse que todas las partes en las que está dividido el total son iguales. Para reforzar. Si lo cree conveniente, puede escribir en la pizarra (con cifras o con letras) distintas fracciones para que los alumnos las escriban de la otra forma y anoten también cuál es su numerador y denominador. Actividades 1 1 2     2 3     2 4     4 6 2 3 4 • Un tercio. •  Un cuarto. •  Dos quintos. •  Dos sextos. •  Cuatro séptimos. •  Tres octavos. •  Cinco novenos. Otras actividades •  Escriba en la pizarra varias fracciones y pida a los alumnos   que las representen en su cuaderno. Por ejemplo: 1 2           2 3           3 4           4 5 Si tienen dificultades, puede sugerirles que, para cada fracción, tienen   que dibujar una figura (la más sencilla es un rectángulo de un cuadradito   de ancho) formada por tantos cuadraditos como indique el denominador de la fracción y colorear tantos cuadraditos como señale el numerador.   Lea después, de forma colectiva, las fracciones y comente algunas   de las representaciones aportadas. 10
  • 11.
    6 Divide decenas, centenas,millares y decenas de millar entre 10 40 : 10 300 : 10 7.000 : 10 20.000 : 10 80 : 10 500 : 10 9.000 : 10 50.000 : 10 60 : 10 400 : 10 5.000 : 10 80.000 : 10 90 : 10 700 : 10 8.000 : 10 90.000 : 10 CÁLCULO MENTAL 30 : 10 5 3 500 : 10 5 50 4.000 : 10 5 400 30.000 : 10 5 3.000 4 Escribe en tu cuaderno cómo se lee cada fracción. 1 3 1 4 2 5 2 6 4 7 3 8 5 9 5 Escribe las fracciones. Dos cuartos. Tres quintos. Cuatro sextos. Tres séptimos. Siete octavos. Seis novenos. Problemas 6 Resuelve. Elena preparó para su cumpleaños estas 3 pizzas y dividió cada una en las partes que se indican: ¿Qué fracción representa un trozo de cada clase de pizza? Si de la pizza de queso se comieron siete octavos, ¿qué fracción de pizza quedó? HAZLO ASÍ 1 2 un medio 2 3 dos tercios 3 4 tres cuartos 4 5 cuatro quintos 1 6 un sexto 3 7 tres séptimos 5 8 cinco octavos 7 9 siete novenos ATÚN QUESO JAMÓN 85 ES0000000024590 663006-Unidad 06_22589.indd 85 10/03/2015 13:16:48 UNIDAD 6 5 •  2 4 •  3 5 •  4 6 •  3 7 •  7 8 •  6 9 6 •  Atún: 1 4 . Queso: 1 8 . Jamón: 1 6 . •  Quedó 1 8 . Cálculo mental • 4 •  30 •  700 •  2.000 •  8 •  50 •  900 •  5.000 •  6 •  40 •  500 •  8.000 •  9 •  70 •  800 •  9.000 Notas Otras actividades •  Puede también trabajar el concepto de fracción de un conjunto (parte de elementos de un conjunto que cumplen una cierta condición).   Saque a la pizarra a un grupo de como máximo 10 alumnos y pida a la clase que digan la fracción que expresa el número de alumnos que cumplen una determinada condición. Por ejemplo: – La fracción de niñas (o de niños) que hay en el grupo. – La fracción de alumnos del grupo que llevan pantalón. – La fracción de alumnos que llevan una prenda de color… Puede repetir la actividad variando el número de personas que forman el grupo, o por equipos de distinto número de miembros, para trabajar distintos denominadores. 11
  • 12.
    Comparación de fracciones ¿Encuántas partes iguales está dividida cada figura? Figura a. … Figura b. … ¿Cuántas partes coloreadas tiene cada figura? Figura a. … Figura b. … ¿Qué fracción representa la parte coloreada de cada figura? ¿Cuál es la fracción mayor? ¿En cuántas partes iguales está dividida cada figura? Figura c. … Figura d. … ¿Cuántas partes coloreadas tiene cada figura? Figura c. … Figura d. … ¿Qué fracción representa la parte coloreada de cada figura? ¿Cuál es la fracción menor? ¿Qué ruleta tiene mayor zona roja? Fíjate en que la ruleta A tiene mayor zona roja que la ruleta B. Por tanto, resulta que: La fracción 5 8 es mayor que la fracción 3 8 . 5 8 . 3 8 ¿Qué ruleta tiene menor zona verde? Fíjate en que la ruleta D tiene menor zona verde que la ruleta C. Por tanto, resulta que: La fracción 1 8 es menor que la fracción 1 4 . 1 8 , 1 4 A CB D 5 8 1 4 3 8 1 8 1 Observa las figuras y contesta en tu cuaderno. a. c. b. d. 86 ES0000000024590 663006-Unidad 06_22589.indd 86 10/03/2015 13:16:49 Propósitos •  Comparar fracciones de igual denominador o numerador. •  Ordenar grupos de fracciones. Sugerencias didácticas Para explicar. Pida a los alumnos que observen en el libro la representación de las fracciones 5/8 y 3/8 y que comparen la parte roja. Señale que la primera figura tiene más parte coloreada que la segunda. Repita el proceso para las fracciones 1/4 y 1/8, de manera que los alumnos realicen la comparación de ambas fracciones de forma gráfica. Una vez realizada la actividad 1, donde se insiste en el trabajo gráfico, deje que los alumnos hagan por sí mismos la actividad 2 para que descubran el procedimiento de comparación a nivel numérico. Muestre la importancia de analizar siempre en primer lugar qué termino tienen en común las dos fracciones para después comparar el otro. Puede ser interesante realizar un mural en el que se ponga por escrito el procedimiento numérico con algún ejemplo. Para reforzar. Escriba varios grupos de fracciones con igual denominador o igual numerador para que los alumnos las ordenen de mayor a menor, o viceversa. Actividades 1 •  Figura a. 6 partes. Figura b. 6 partes. •  Figura a. 4 partes. Figura b. 2 partes. •  Figura a. 4 6 . Figura b. 2 6 . Fracción menor: 2 6 . •  Figura c. 6 partes. Figura d. 1 parte. •  Figura a. 1 parte. Figura b. 1 parte. Otras actividades •  Dibuje en la pizarra la siguiente figura y pida a los alumnos que la copien en sus cuadernos y coloreen el número de cuadrados que quieran. A continuación, agrupe a los alumnos por parejas y formule a cada pareja las siguientes preguntas: –  ¿Cuál de los dos ha coloreado más (o menos) parte de la figura? – ¿Qué fracción de la figura habéis coloreado cada uno? ¿Qué término coincide en ambas fracciones? – ¿Cuál de las dos fracciones tiene el numerador mayor (o menor)? ¿Cuál de las dos fracciones es mayor (o menor)? 12
  • 13.
    Escribe tres fraccionesmás en cada serie y contesta. ¿Cuál es la fracción mayor en la serie a.? ¿Cuál es la fracción menor en la serie b.? RAZONAMIENTO Problemas 4 Resuelve. Marcos tiene dos cartulinas iguales, una roja y otra azul. Divide las dos en 8 partes iguales y utiliza 3 partes de cartulina roja y 5 partes de cartulina azul. ¿De qué color utiliza más? Nuria y Jorge tienen cada uno una ruleta de la misma forma y tamaño. La ruleta de Nuria está dividida en 9 partes iguales y la de Jorge en 8. Cada ruleta tiene 5 partes de rojo. ¿Qué ruleta tiene mayor zona de rojo? En una ciudad, tres séptimos de los productos reciclados son envases de vidrio, dos séptimos son envases de aluminio y un séptimo de plástico. ¿De qué tipo se recicla más? a. 1 2 , 1 3 , 1 4 b. 1 7 , 2 7 , 3 7 2 Copia y colorea en cada figura la fracción indicada. Después, completa en tu cuaderno. 3 Piensa y escribe las fracciones que se indican. Cuatro fracciones mayores que 2 7 y menores que 7 7 . Cuatro fracciones mayores que 1 9 y menores que 1 2 . 2 4 3 4 3 4 3 6 2 4 2 4 3 4 4 6 3 4 3 6 Las dos fracciones tienen igual el denominador. Compara los … Es menor la fracción de numerador menor. Las dos fracciones tienen igual el … Compara los … Es mayor la fracción de denominador menor. 6 87 ES0000000024590 663006-Unidad 06_22589.indd 87 17/03/2015 11:58:35 UNIDAD 6 •  Figura a. 1 6 . Figura b. 1 2 . Fracción menor: 1 6 . 2 Compara los numeradores. 2 4 , 3 4 Compara los denominadores. 3 4 . 3 6 3 •  3 7 , 4 7 , 5 7 , 6 7     •  1 8 , 1 7 , 1 6 , 1 5 4 • 3 8 , 5 8 . Utiliza más azul. •  5 9 , 5 8 . La ruleta de Jorge tiene más zona de color rojo. •  1 7 , 2 7 , 3 7 . Se reciclan más envases de vidrio. Razonamiento a.  1 5 , 1 6 , 1 7 b.  4 7 , 5 7 , 6 7 •  Fracción mayor: 1 2 . •  Fracción menor: 1 7 . Notas Otras actividades •  Dibuje en la pizarra tres rectángulos iguales divididos en 3, 4 y 6 partes iguales, respectivamente. Forme grupos de tres alumnos y pídales que cada uno copie las figuras y coloree dos partes en cada una. Después, pregúnteles: –  ¿Qué fracción habéis coloreado en cada figura? ¿Qué término coincide en las tres fracciones? –  ¿Cuál de las tres fracciones tiene el denominador menor (o mayor)? ¿Cuál de las tres fracciones es mayor (o menor)? 13
  • 14.
    Fracción de unnúmero 1 Calcula en tu cuaderno. 5 6 de 30 3 7 de 77 5 8 de 96 2 5 de 130 4 9 de 189 2 Contesta en tu cuaderno. ¿Cuántos centímetros son medio metro? 1 2 de 100 5 … ¿Cuántos gramos son un cuarto de kilo? ¿Cuántos minutos son 3 cuartos de hora? 3 Piensa y contesta sin calcular. ¿Qué es mayor: 4 5 de 20 o 2 5 de 20? ¿Qué es menor: 2 7 de 70 o 2 7 de 140? En la clase de 4.º hay 20 pinturas de cera. 3 4 de las pinturas son de color rojo. ¿Cuántas pinturas rojas hay? 3 4 de 20 5 15 Hay 15 pinturas rojas. Para calcular la fracción de un número: 1.º Divide el número entre el denominador de la fracción. 2.º Multiplica el cociente obtenido por el numerador de la fracción. Calcula 3 4 de 20 1.º Divide el número, 20, entre el denominador de la fracción, 4. 20 : 4 5 5 2.º Multiplica el cociente obtenido, 5, por el numerador de la fracción, 3. 5 3 3 5 15 EJEMPLO 5 6 de 30 30 : 6 5 …; … 3 5 5 … 5 6 de 30 5 … RECUERDA 1 metro 5 100 centímetros 1 kilogramo 5 1.000 gramos 1 hora 5 60 minutos 88 ES0000000024590 663006-Unidad 06_22589.indd 88 10/03/2015 13:16:52 Propósitos •  Calcular la fracción de un número. •  Resolver situaciones reales   en las que hay que calcular   la fracción de un número. Sugerencias didácticas Para explicar. Lea el problema propuesto y comente que en este caso calculamos la fracción de   un número, no de una figura. Explique los pasos a seguir, relacionándolo   con la idea de fracción vista hasta entonces: 3/4 de una unidad significa que de una unidad dividida en   4 partes iguales, cogemos 3 de las partes; de forma similar, para calcular 3/4 de 20 pinturas, dividimos 20 entre 4 y el resultado lo multiplicamos por 3. Si lo cree conveniente, puede trabajar con los alumnos este proceso manipulativamente. Haga en común la actividad 1  y ponga otros ejemplos para resolver de forma colectiva en la pizarra. Resuelva también entre todos   el primer problema, razonando   en común qué se debe calcular   y cómo se hace. Actividades 1 •  5 6 de 30 5 25 •  3 7 de 77 5 33 •  5 8 de 96 5 60 •  2 5 de 30 5 12 •  4 9 de 189 5 84 2 •  1 2 de 100 cm 5 50 cm •  1 4 de 1.000 g 5 250 g •  3 4 de 60 s 5 45 s 3 • 4 5 . 2 5 , luego 4 5 de 20 es mayor. •  70 , 140, luego 2 7 de 70   es menor. Otras actividades • Escriba en la pizarra varias fracciones de un número, para que los alumnos las copien y calculen en el cuaderno. Después, entregue a cada alumno un montoncito de garbanzos para que comprueben manipulativamente sus resultados siguiendo estos pasos: 1.º  Coger los garbanzos que indica el número. 2.º  Repartir los garbanzos en tantos grupos iguales como indica   el denominador de la fracción. 3.º  Contar los garbanzos que hay en el número de grupos que indica   el numerador de la fracción. 14
  • 15.
    6 Problemas 4 Resuelve. En unabolsa hay 80 bombones. En un parque hay 160 bancos. 3 4 de los bombones son de fresa. 5 8 de los bancos son métalicos. ¿Cuántos bombones son de fresa? ¿Cuántos bancos no son metálicos? 5 Piensa y resuelve. En una clase hay 24 alumnos. De ellos, 2 8 vienen a clase caminando y 1 6 viene en autobús. ¿Cuántos alumnos de la clase vienen caminando? ¿Y en autobús? Hay 90 árboles frutales en el huerto. Un sexto de ellos son manzanos y tres quintos son perales. ¿Cuántos manzanos hay? ¿Y perales? En la biblioteca del colegio hay 250 libros. Tres quintos son cuentos, un décimo novelas y el resto son diccionarios. ¿Cuántos libros hay de cada tipo? Mónica tiene en su vivero 182 plantas. Dos séptimos son pinos y la mitad de los pinos son piñoneros. ¿Cuántos pinos piñoneros tiene? 6 Inventa y resuelve. Utiliza los datos 2 5 y 60 e inventa un problema. Después, resuélvelo y comprueba que lo has hecho bien. Divide centenas y millares entre 100 y entre 1.000 300 : 100 7.000 : 100 2.000 : 1.000 500 : 100 9.000 : 100 4.000 : 1.000 700 : 100 5.000 : 100 6.000 : 1.000 900 : 100 8.000 : 100 9.000 : 1.000 CÁLCULO MENTAL 900 : 100 5 9 6.000 : 100 5 60 7.000 : 1.000 5 7 60 2 5 89 ES0000000024590 663006-Unidad 06_22589.indd 89 10/03/2015 13:16:53 UNIDAD 6 4 •  3 4 de 80 5 80 Son de fresa 60. •  5 8 de 160 5 100 160 – 100 5 60 No son metálicos 60 bancos. 5 •  2 8 de 24 5 6; 1 6 de 24 5 4 Vienen caminando 6 alumnos y en autobús 4. •  1 6 de 90 5 15; 3 5 de 90 5 54 Hay 15 manzanos y 54 perales. •  3 5 de 250 5 150 1 10 de 250 5 25 250 2 (150 1 25) 5 75 Hay 150 cuentos, 25 novelas y 75 diccionarios. •  2 7 de 182 5 52; 1 2 de 52 5 26 Tiene 52 pinos y 26 de ellos son pinos piñoneros. 6 R. M. En un almacén hay 60 cajas. 2 5 de las cajas contienen balones. ¿Cuántas cajas con balones hay en el almacén? 2 5 de 60 5 24 En el almacén hay 24 cajas con balones. Cálculo mental •  3 •  70 •  2 •  5 •  90 •  4 •  7 •  50 •  6 •  9 •  80 •  9 Notas Otras actividades • Plantee de forma oral problemas similares a los propuestos en esta página del libro, para resolverlos en común. Por ejemplo: 2 Inés tiene 12 batidos. Un tercio de los batidos son de fresa, dos cuartos son de chocolate y un sexto son de vainilla. ¿Cuántos batidos tiene Inés de cada sabor? 2 Álvaro tiene un juego con 20 fichas. Un cuarto de las fichas son azules, dos quintos son rojas y el resto son verdes. ¿Cuántas fichas de cada color tiene el juego? 15
  • 16.
    Fracciones propias eimpropias 1 Fíjate en los términos de cada fracción y escribe en tu cuaderno si es mayor, menor o igual que la unidad. 5 6 10 8 6 6 7 5 4 4 8 9 13 10 2 Compara estas fracciones y números naturales. HAZLO ASÍ Compara 25 3 y 8 1.º Divide el numerador de la fracción entre el denominador y compara el cociente con el número natural. 2.º Si el cociente es menor, es mayor el número natural. En cualquier otro caso, es mayor la fracción. 12 2 5 3 23 3 13 5 3 6 17 2 19 4 4 Jon, Nicolás y Silvia están pintando cartulinas. ¿Qué fracción representa la parte pintada por cada uno? Jon Nicolás Silvia Ha pintado 4 6 . Ha pintado 6 6 5 1. Ha pintado 9 6 . La fracción 4 6 tiene el numerador menor que el denominador. Es una fracción propia y es menor que la unidad: 4 6 , 1. La fracción 6 6 tiene iguales su numerador y su denominador. Es igual a la unidad: 6 6 5 1. La fracción 9 6 tiene el numerador mayor que el denominador. Es una fracción impropia y es mayor que la unidad: 9 6 . 1. 8 5 8 25 3 . 8 2 5 3 1 8 90 Propósitos •  Reconocer fracciones propias   e impropias. •  Comparar fracciones y números naturales. Sugerencias didácticas Para explicar. Pida a los alumnos que lean la situación planteada   y se fijen en la parte de cartulina   que ha pintado cada uno. Caracterice las fracciones propias e impropias   y muestre la importancia de comparar siempre los dos términos para poder diferenciarlas. Trabaje en común el Hazlo así de la actividad 2, mostrando la técnica para comparar fracciones impropias y números naturales. Deje claro que toda fracción propia   es siempre menor que la unidad. Actividades 1 Mayores que la unidad: 10 8 , 7 5 y 13 10 . Iguales que la unidad: 6 6 y 4 4 . Menores que la unidad: 5 6 y 8 9 . 2 Conviene realizar el ejemplo resuelto en común, explicando que, para comparar una fracción   y un número natural, primero hay que calcular el cociente de la fracción y, después, comparar dicho cociente con el número natural. •  12 2 . 5 •  3 , 23 3 •  13 5 , 3 •  6 , 17 2 •  19 4 . 4 Notas Otras actividades •  Escriba en la pizarra varias fracciones en las que a cada una   le falte un término. Por ejemplo: 4               5               8               2             3             4 Elija una fracción en la que falte el numerador y propóngales que lo inventen para que la fracción sea mayor, menor e igual a la unidad. Después,   haga una puesta en común con los resultados. Proceda de forma análoga   con alguna fracción en la que falte el denominador. 16
  • 17.
    96Números mixtos 1 Escribeel número mixto y la fracción que representa la parte coloreada. Fíjate en cuántas figuras completas hay. 2 Copia en tu cuaderno y representa cada número mixto. En la pizzería venden pizzas partidas en 8 trozos iguales. Miguel ha comprado 20 porciones para invitar a merendar a unos amigos. 20 8 de pizza son 2 pizzas y 4 8 de otra. 20 8 se escribe así: 2 4 8 . El número 2 4 8 es un número mixto y está formado por un número natural y una fracción. Un número mixto está formado por un número natural y una fracción. 2 pizzas Copia y rodea en tu cuaderno el número mixto mayor de cada pareja. RAZONAMIENTO 3 4 7 2 4 7 5 2 9 5 6 9 2 3 7 4 5 7 20 8 4 8 1 3 4 1 1 2 1 2 3 91 UNIDAD 6 Propósitos •  Reconocer un número mixto. •  Interpretar y representar números mixtos. Sugerencias didácticas Para explicar. Lea la situación propuesta y pida a los alumnos   que se fijen en la representación gráfica de las porciones de pizza. Muestre que 20 porciones son   2 pizzas completas y 4 porciones   de otra. Escriba en la pizarra   la fracción y el número mixto, haciéndoles ver la relación entre uno   y otro. Señale que todo número mixto está formado por un número natural (figuras enteras) y una fracción propia (partes de una figura). Actividades 1 1 2 3 5 5 3 2 2 5 5 12 5 1 2 4 5 6 4 2 Razonamiento Pida a los alumnos que expresen   sus ideas para resolver la actividad. Coméntelas señalando que una forma de resolverla es escribiendo cada número mixto en forma de fracción y comparando las fracciones obtenidas, o bien comparando las partes enteras de los números mixtos y si son iguales, las fracciones propias. 25 7 . 18 7     Es mayor 3 4 7 . 47 9 , 51 9     Es mayor 5 6 9 . 17 7 , 33 7     Es mayor 4 5 7 . Competencias •  Conciencia y expresión cultural. Las representaciones gráficas   son un componente fundamental a la hora de trabajar con fracciones   y números mixtos. Trabaje en común actividades similares a la actividad 2   en las que los alumnos tengan que realizar representaciones por sí mismos. Ayúdeles pidiéndoles que determinen en primer lugar, mirando el denominador de la fracción propia, en cuántas partes deben dividir cada unidad. Puede pedirles también que realicen dibujos utilizando representaciones   de números mixtos y que sus compañeros escriban qué números mixtos   se han utilizado. Inteligencia espacial 17
  • 18.
    Averigua los datosque faltan en cada problema e invéntalos. Después, resuelve. 1 Marcos tiene 75 años, Luisa algunos menos que él y Teo menos que Luisa. ¿Cuántos años tienen entre los tres? 2 Laura tenía varias bolsas iguales de patatas. Vendió 35 kilos. ¿Cuántos kilos de patatas le sobraron? 3 César tenía varios billetes de 20 €. Prestó algunos a su hermana. ¿Cuánto dinero le quedó? 4 Marta es más alta que su hermana Paula. ¿Cuántos centímetros es más alta Marta que Paula? Vamos a leer el problema, averiguar los datos que faltan para resolverlo e inventar un valor para ellos. Después, lo resolveremos. Esta noche, en el restaurante, han pedido manzana de postre 14 personas, han pedido pera algunas personas menos y naranja algunas personas más. ¿Cuántas personas han pedido de postre fruta? 1.º Comprende. Datos Han pedido manzana 14 personas. Algunas personas menos han pedido pera, y algunas más han pedido naranja. Pregunta ¿Cuántas personas han pedido de postre fruta? Para resolver el problema hay que saber cuántas personas han pedido pera y cuántas naranja. Inventamos unos valores que cumplan el enunciado. Por ejemplo: han pedido pera 10 personas y naranja 20 personas. 2.º Piensa qué hay que hacer. Hay que sumar todas las personas que han pedido de postre fruta. 3.º Calcula. 14 1 10 1 20 5 44 Solución: Han pedido de postre fruta 44 personas. 4.º Comprueba. Revisa si lo has hecho bien. Averiguar e inventar los datos que faltan Solución de problemas 92 ES0000000024590 663006-Unidad 06_22589.indd 92 10/03/2015 13:16:58 Propósitos •  Resolver problemas averiguando   e inventando los datos que faltan. •  Completar unos cálculos e inventar problemas que se resuelvan   con dichos cálculos. Sugerencias didácticas Para explicar. Haga que los alumnos lean detenidamente el problema   y pregúnteles qué operación hay que realizar para resolverlo y qué datos hay que utilizar. Explique cuáles son los datos que faltan y muestre que se han inventado para esos datos unos valores que cumplen las condiciones del enunciado. Pídales que ellos mismos propongan otros valores posibles que cumplan también las condiciones, y que después resuelvan los problemas que hayan obtenido. Actividades 1 R. M. Marcos tiene 75 años, Luisa 5 años menos que él y Teo 5 años menos que Luisa. ¿Cuántos años tienen entre los tres?  75 1 70 1 65 5 210  Entre los tres tienen 210 años. 2 R. M. Laura tenía 9 bolsas   de patatas de 12 kg cada una.   Vendió 35 kilos. ¿Cuántos kilos  de patatas le sobraron?  12 3 9 2 35 5 73  Le sobraron 73 kg de patatas. 3 R. M. César tenía 7 billetes de 20 €. Prestó 2 billetes a su hermana. ¿Cuánto dinero le quedó?  7 3 20 2 2 3 20 5 100  Le quedaron 100 €. 4 R. M. Marta mide 135 cm   y su hermana Paula 116 cm. ¿Cuántos centímetros es más alta Marta que Paula?  135 2 116 5 19  Marta mide 19 cm más que Paula. 5 R. M. David compró 3 libros por   9 € cada uno y una bufanda   por 12 €. ¿Cuánto dinero gastó David?  3 3 9 1 12 5 39  David gastó 39 €. Otras actividades •  Agrupe a los alumnos por parejas e indique a cada alumno que   le diga a su compañero dos cálculos sencillos (hechos mentalmente),  para que este los escriba en una hoja e invente el enunciado de un problema, que se resuelva con dichos cálculos. A continuación, entre los dos resolverán el problema inventado comprobando si realizan los dos cálculos   propuestos al principio. 18
  • 19.
    Inventa y completaen tu cuaderno los números que faltan en los cálculos. Después, escribe un problema que se resuelva con ellos. 6 Inventa los datos que faltan en cada problema. Fíjate después si tiene sentido y resuélvelo en tu cuaderno. 5 David compró varios libros, todos del mismo precio. Después, se compró una bufanda que era algo más cara que un libro. ¿Cuánto dinero gastó David? 6 Un perro grande pesa bastantes kilos. Un gato pesa mucho menos que él y un perro pequeño pesa casi igual que un gato. ¿Cuánto pesan los tres juntos? 7 En un vagón de tren iban varias personas. Al llegar a una parada, se bajaron algunas y subieron más personas de las que se bajaron. ¿Cuántas personas iban en el tren tras esa parada? 8 Marta compró varias cajas iguales de bombones. Jacinto compró el doble de bombones que ella. ¿Cuántos bombones compró Jacinto? 9 Ramón tenía unos ahorros. Su madre le dio un billete y después se compró un chándal. ¿Cuánto dinero le quedó? INVENTA TUS PROBLEMAS Inventa y completa en tu cuaderno los números que faltan en los cálculos. Después, escribe un problema que se resuelva con ellos. 70 1 ... 5 ... ... 1 10 5 ... 1 50 2 ... 5 ... ... 1 40 5 ... 3 6 3 ... 5 ... ... 1 8 5 ... 2 4 3 ... 5 ... 2 3 ... 5 ... 4 93 ES0000000024590 663006-Unidad 06_22589.indd 93 10/03/2015 13:17:00 UNIDAD 6 6   R. M. Un perro grande pesa 19 kg. Un gato pesa 2 kg y un perro pequeño pesa 3 kg. ¿Cuánto pesan los tres juntos? 19 1 2 1 3 5 24 Los tres juntos pesan 24 kg. 7   R. M. En un vagón de tren iban 45 personas. Al llegar a una parada se bajaron 17 personas y subieron 23. ¿Cuántas personas iban en el tren tras esa parada? 45 2 17 1 23 5 51 En el tren iban 51 personas. 8   R. M. Marta compró 3 cajas de bombones con 24 bombones cada una. Jacinto compró el doble de bombones que ella. ¿Cuántos bombones compró Jacinto? 3 3 24 3 2 5 144 Jacinto compró 144 bombones. 9   R. M. Ramón tenía ahorrados 85 €. Su madre le dio un billete de 20 € y después se compró un chándal por 59 €. ¿Cuánto dinero le quedó? 85 1 20 2 59 5 46 Le quedaron 46 €. Inventa tus problemas Realice el primer problema en común. Pida a un alumno que salga a la pizarra y exponga al resto de la clase su propuesta para completar los cálculos y un problema asociado. Entre todos se comprobará si la propuesta es o no correcta. Después, haga que realicen el resto de los problemas de forma individual y compruebe los resultados en común. 1   R. M. 70 1 40 5 110 110 1 10 5 120 Felipe tiene en su granja 70 corderos y 40 gallinas. Hoy ha comprado 10 corderos más. ¿Cuántos animales en total tiene ahora Felipe? 2   R. L. 3   R. L. 4   R. L. Competencias •  Iniciativa y emprendimiento. Las actividades de invención de problemas son un contexto muy adecuado para desarrollar esta competencia. Pida a los alumnos, a la hora de trabajar las actividades de esta página, que tengan cuidado al completar los cálculos y anímelos a ser creativos cuando planteen los problemas. Recuérdeles la importancia de comprobar que el problema que han planteado se resuelve con dichos cálculos. Inteligencia intrapersonal 19
  • 20.
    6 Completa loshuecos. 3 7 , 7 4 8 . 4 6 . 6 10 , 10 7 Calcula. 3 8 de 16 3 8 de 88 9 10 de 500 6 7 de 147 2 3 de 2.340 4 5 de 6.925 8 VOCABULARIO. Explica qué son las fracciones impropias y cómo puedes reconocerlas. 9 Escribe en tu cuaderno, para cada fracción, si es mayor, menor o igual que la unidad. 9 9 7 4 4 7 8 9 6 2 10 Compara. Escribe el signo adecuado. 11 2 y 4 3 y 8 3 17 5 y 2 5 y 22 4 11 Escribe el número mixto y la fracción representados en cada figura. 12 Escribe un número mixto y represéntalo en tu cuaderno. 1 Escribe la fracción que representa la parte coloreada e indica cuáles son sus términos. 2 Escribe cómo se lee cada fracción. 3 7 1 2 2 4 4 5 5 6 3 8 7 9 9 10 3 Expresa con cifras. Un quinto. Cuatro octavos. Dos sextos. Un tercio. Cinco décimos. Tres cuartos. Tres novenos. Dos séptimos. 4 Copia y colorea para que la descripción sea cierta. Seis décimos de los globos son azules y el resto son rojos. 5 Compara. 5 6 5 7 6 10 3 10 5 8 3 8 4 9 4 5 ACTIVIDADES 94 ES0000000024590 663006-Unidad 06_22589.indd 94 10/03/2015 13:17:01 Propósitos •  Repasar y afianzar los contenidos básicos de la unidad. Actividades 1   5 8 ; 6 10 ; 4 9 ; 4 5 2   •  Tres séptimos. •  Un medio. •  Dos cuartos. •  Cuatro quintos. •  Cinco sextos. •  Tres octavos. •  Siete novenos. •  Nueve décimos. 3   •  1 5 •  2 6 •  15 10 •  3 9 •  4 8 •  1 3 •  3 4 •  2 7   4   6 10 de 10 5 6 Rojos: 6, azules: 4. 5   •  5 6 . 5 7 •  6 10 . 3 10 •  5 8 . 3 8 •  4 9 , 4 5 6   R. M. •  3 7 , 5 7 •  4 8 . 4 10 •  6 8 . 6 9 •  4 10 , 7 10 7   •  6 •  33 •  450 •  126 •  1.560 •  5.540 8   Las fracciones impropias son mayores que la unidad y tienen el numerador mayor que el denominador. 9  Mayores: 7 4 y 6 2 . Igual: 9 9 . Menores: 4 7 y 8 9 . 10  •  11 2 . 4 •  3 . 8 3 •  17 5 . 2 •  5 , 22 4 11  • 1 3 6 5 9 6 •  2 1 2 5 5 2 Otras actividades •  Nombre varias fracciones para que los alumnos las escriban en el cuaderno al dictado. Por ejemplo: 1 2     3 5     2 3     5 7     3 2     2 4     4 5     5 6 Después, corríjalas pidiendo a varios alumnos que las lean por orden para que otro compañero las escriba en la pizarra. A continuación, puede trabajar con estas fracciones el reconocimiento de sus términos, su representación, o la comparación de las fracciones que tengan el mismo denominador o el mismo numerador, tanto a nivel colectivo en la pizarra o de forma individual en el cuaderno. 20
  • 21.
    15 Resuelve. Marta trabajaen una oficina. Se encarga de comunicarse por teléfono y por correo electrónico con varias empresas. ¿Cuántas llamadas ha hecho Marta a empresas que no son nacionales? ¿Qué fracción de las llamadas han sido? ¿Ha enviado más correos a España o a Europa? ¿Puedes saberlo sin hacer cálculos? ¿Cómo? ¿Cuántos correos ha enviado a Europa? ¿Cuántos ha enviado a América? ¿Cómo lo has averiguado? Problemas 13 Piensa y resuelve. En una fiesta se repartieron 3 tartas en partes iguales entre 10 niños. ¿Qué fracción de tarta le correspondió a cada uno? ¿Fueron más o menos de cuatro décimos? Begoña vende bizcochos partidos en 2 partes iguales. Ha vendido 13 partes. ¿Cuántos bizcochos enteros y partes de bizcocho ha vendido? Exprésalo con un número mixto. 14 Resuelve. Marcos y Concha han partido una barra de pan en 8 partes iguales. Marcos ha comido cinco octavos y Concha ha comido menos que él. ¿Qué fracción de barra ha podido comer Concha? Pedro tiene bombones de varios tipos. Dos octavos son de fresa, un octavo de menta y el resto de avellana. ¿De qué tipo hay más bombones? ¿Y menos? En el colegio hay 250 alumnos. Cuatro quintos de ellos comen en el comedor. ¿Cuántos alumnos comen en el comedor? ¿Cuántos no comen en él? 15 Resuelve. Marta trabaja en una oficina. Se encarga de comunicarse por teléfono y por correo electrónico con varias empresas. ¿Cuántas llamadas ha hecho Marta a empresas que no son nacionales? ¿Qué fracción de las llamadas han sido? ¿Ha enviado más correos a España o a Europa? ¿Puedes saberlo sin hacer cálculos? ¿Cómo? ¿Cuántos correos ha enviado a Europa? ¿Cuántos ha enviado a América? ¿Cómo lo has averiguado? 6 16 Ayer me comí tres cuartos de las peras que tenía. Hoy he comido 2 peras, que eran las que me quedaban. ¿Cuántas peras tenía? Demuestra tu talento 180 llAMADAS 4 5 a empresas nacionales 595 CorrEoS 4 7 a España, 2 7 a Europa y el resto a América 95 ES0000000024590 663006-Unidad 06_22589.indd 95 10/03/2015 13:17:02 UNIDAD 6 12  R. M. 1 1 4 5 5 4 13  •  Le correspondió 3 10 de tarta a cada uno; es decir, menos de cuatro décimos. •  13 2 5 6 1 2 . Ha vendido 6 bizcochos y medio. 14  • Ha podido comer 1 8 , 2 8 o 3 8 . •  Fresa: 2 8 . Menta: 1 8 . Avellana: 5 8 . Hay más de avellana y menos de menta. •  4 5 de 250 5 200 250 2 200 5 50 Comen 200 alumnos y no comen 50. 15  •  4 5 de 180 5 144 180 2 144 5 36 Ha hecho 36 llamadas. •  Han sido 1 5 de las llamadas. •  4 7 . 2 7 . Más a España. •  2 7 de 595 5 170 Ha enviado 170 correos a Europa. •  1 7 de 595 5 85 Ha enviado 85 correos a América. Demuestra tu talento 16  2 peras son 1 4 de las peras, luego el total de las peras es 8. Notas Competencias •  Competencia social y cívica. Al realizar la actividad 15, puede llevar a cabo un debate con los alumnos sobre distintos temas relacionados con la competencia y con el contexto que aparece en ella: el mundo del trabajo y la relación con personas de otras empresas y países. Pida a los alumnos que enuncien conductas o valores positivos que deban tener lugar en ese entorno y cómo pueden influir en una relación cordial y productiva. 21
  • 22.
    Comprender noticias confracciones 1 Lee la noticia y resuelve. ¿Qué fracción de los asistentes a yoga correspondió a adultos? ¿Y de los asistentes a gimnasia? ¿Cuál de las dos fracciones es mayor? ¿Qué fue mayor: la fracción de mayores asistentes a yoga o la fracción de adultos? ¿Cómo lo has averiguado? ¿Cuántos jóvenes asistieron a yoga? ¿Cuántos mayores asistieron a gimnasia? Ordena, de menor a mayor número, los tipos de asistentes a yoga. ¿Cómo lo has hecho? 2 TRABAJO COOPERATIVO. Averigua con tu compañero si estas oraciones son correctas. Si es posible, hacedlo sin calcular. Hubo más mayores en yoga que jóvenes. Hubo más mayores en gimnasia que en yoga. Hubo más jóvenes en yoga que mayores. SABER HACER El pueblo del deporte En la localidad de Villares se celebró ayer la XII Jornada Deportiva municipal. Gente de todas las edades participó, superando la asistencia de otros años. Por ejemplo, mil doscientas personas probaron la actividad de yoga y ochocientas personas se acercaron a la zona de gimnasia. La distribución por edades fue la siguiente: Jóvenes Adultos Mayores Yoga Gimnasia 96 ES0000000024590 663006-Unidad 06_22589.indd 96 10/03/2015 13:17:05 Propósitos •  Desarrollar la competencia matemática resolviendo situaciones de la vida real. •  Repasar contenidos clave. Actividades pág. 96 1   •  Adultos en yoga: 2 6 . Adultos en gimnasia: 2 8 . Es mayor la de adultos en yoga. •  Mayores en yoga: 1 6 . Adultos en yoga: 2 6 . Es mayor la de adultos en yoga. •  3 6 de 1.200 5 600 Asistieron a yoga 600 jóvenes. •  2 8 de 800 5 200 Asistieron a gimnasia   200 mayores. •  Mayores , adultos , jóvenes 2   •  1 6 , 3 6 . Falso. •  2 8 . 1 6 . Verdadero. •  3 6 . 1 6 . Verdadero. Actividades pág. 97 1   •  320.500. Trescientos veinte mil quinientos. •  706.096: Setecientos seis mil noventa y seis. •  2.700.009. Dos millones setecientos mil nueve. •  6.091.000. Seis millones noventa y un mil. 2   •  5.821 •  538 •  10.574 •  4.025 •  12.717 •  36.028 3   •  28.623 •  c 5 958, r 5 8 •  175.820 •  271 •  349.520 •  c 5 378, r 5 17 4   •  8 2 2 5 6 •  7 3 4 5 28 •  3 2 3 5 0 •  10 1 4 5 14 •  9 2 8 5 1 •  6 : 3 5 2 Desarrollo de la competencia matemática •  Los contextos reales de aplicación de lo aprendido en la unidad permiten   un desarrollo potente de esta competencia. El contexto ofrecido, las noticias en medios de comunicación, resulta próximo a los alumnos. Al comprobar las respuestas, preste especial atención a las explicaciones de los alumnos sobre sus procesos de razonamiento. Cuando realicen el trabajo cooperativo, pida a cada grupo que aporte varias afirmaciones correctas más, utilizando los gráficos de la página, y que den también razón de cómo han analizado la corrección de las tres afirmaciones propuestas. Inteligencia interpersonal 22
  • 23.
    4 Calcula. 8 2(5 2 3) (9 2 2) 3 4 8 2 5 2 3 10 1 8 : 2 9 2 2 3 4 (8 2 2) : 3 5 Estima estas operaciones. 675 1 492 2.708 1 1.611 914 2 236 5.333 2 2.638 675 3 2 3.194 3 7 6 Escribe el número que representa cada número romano. VI XIII CIV MCM 7 Completa. 8 3 (2 1 …) 5 8 3 … 1 8 3 4 (7 2 3) 3 … 5 … 3 5 2 … 3 5 1 Escribe el número y cómo se lee. 3 CM 1 2 DM 1 5 C 7 CM 1 6 UM 1 9 D 1 6 U 2 U. de millón 1 7 CM 1 9 U 6 U. de millón + 9 DM 1 1 UM 2 Calcula. 1.039 1 4.782 3.456 2 2.918 9.675 1 899 4.911 2 886 12.099 1 618 37.902 2 1.874 3 Calcula. Después, haz la prueba de las divisiones. 329 3 87 8.630 : 9 745 3 236 6.504 : 24 1.028 3 340 13.247 : 35 8 Los 312 alumnos de un colegio van a viajar en autobuses con capacidad para 52 plazas cada uno. ¿Cuántos autobuses serán necesarios? 9 Marisol tenía 8 billetes de 20 € y 3 billetes menos de 50 €. Quiere comprar una lavadora que cuesta 400 €. ¿Tendrá suficiente dinero? 10 Eugenio le dice a su nieta Elena: ¿Qué es mejor: recibir cada día del año 20 € o cada mes del año 600 €? 11 En el almacén envasaron 1.500 kg de lentejas en sacos de 12 kg. Vendieron 80 sacos. ¿Cuántos kilos de lentejas les quedaron? 12 Mercedes compró 25 sillas a 90 € cada una. Las vendió 18 € más caras, pero le quedaron 4 sillas sin vender. ¿Ganó dinero? ¿Cuánto? 13 Raúl tenía 20 rollos de cuerda de 18 m cada uno. Los ha cortado en trozos de 5 m. ¿Cuántos trozos de 5 m ha obtenido? ¿Y de 3 metros? Problemas REPASO ACUMULATIVO 6 97 ES0000000024590 663006-Unidad 06_22589.indd 97 10/03/2015 13:17:06 UNIDAD 6 5   •  700 1 500 5 1.200 •  900 2 200 5 700 •  700 3 2 5 1.400 •  3.000 1 2.000 5 5.000 •  5.000 2 3.000 5 2.000 •  3.000 3 7 5 21.000 6   •  6      •  13      •  104      •  1.900 7   •  8 3 (2 1 4) 5 8 3 2 1 8 3 4 5 5 48 •  (7 2 3) 3 5 5 7 3 5 2 3 3 5 5 5 20 8   312 : 52 5 6  Serán necesarios 6 autobuses. 9  8 3 20 1 5 3 50 5 410  410 . 400 Sí, tendrá suficiente dinero. 10 365 3 20 5 7.300  12 3 600 5 7.200 Es mejor cada día 20 €. 11  1.500 : 12 5 125 125 2 80 5 45 45 3 12 5 540 Quedaron 540 kg de lentejas. 12 25 3 90 5 2.250  (90 1 18) 3 21 5 2.268 2.268 2 2.250 5 18 Mercedes ganó 18 €. 13  18 : 5   c 5 3, r 5 3 De cada rollo obtiene 3 trozos de 5 m y 1 trozo de 3 m. En total ha obtenido 60 trozos de 5 m y 20 trozos de 3 m. Notas Repaso en común •  Pida a los alumnos que realicen de forma individual las actividades propuestas en esta página. Después, haga una puesta en común con los resultados obtenidos para detectar las dificultades. Puede pedir también a los alumnos que digan en qué actividades han tenido más problemas. Si lo cree conveniente, proponga otras actividades similares a las propuestas para reforzar los contenidos. 23
  • 24.
    Números decimales7 Contenidos dela unidad SABER NÚMEROS Y OPERACIONES • Unidades decimales. • Números decimales. • Comparación de decimales. • Aproximación de decimales. SABER HACER NÚMEROS Y OPERACIONES • Reconocimiento de las unidades decimales y sus equivalencias. • Escritura de unidades decimales en forma de fracción y de número decimal. • Lectura y escritura de números decimales. • Diferenciación de la parte entera y decimal de un número decimal. • Descomposición, ordenación y comparación de números decimales. • Aproximación de números decimales a un orden dado. RESOLUCIÓN DE PROBLEMAS • Resolución de problemas ordenando primero los datos. • Ordenación de los datos e invención de una pregunta que se resuelva usando todos ellos.   TAREA FINAL • Estudiar la evolución de un precio. SABER SER FORMACIÓN EN VALORES • Valoración de la utilidad de los decimales para comprender diversas situaciones reales. • Interés por la resolución de problemas. 24
  • 25.
    BIBLIOTECA DEL PROFESORADO Programacióndidáctica de aula Recursos para la evaluación • Evaluación de contenidos. Unidad 7: pruebas de control B y A. • Evaluación por competencias. Prueba 7. •  Rúbrica. Unidad 7. Enseñanza individualizada • Plan de mejora. Unidad 7. • Programa de ampliación. Unidad 7. Proyectos de trabajo cooperativo • Proyecto del segundo trimestre. Recursos complementarios • Fichas para el desarrollo de la inteligencia. • Operaciones y problemas. Aprendizaje eficaz • Técnicas de estudio y presentación de exámenes. Proyectos interdisciplinares • Programa de Educación en valores. • Programa de Educación emocional. • Inteligencias múltiples. RECURSOS DIGITALES LibroMedia • Unidad 7: actividades y recursos. MATERIAL DE AULA Láminas OTROS MATERIALES DEL PROYECTO Cuaderno del alumno • Segundo trimestre. Unidad 7. Solución de problemas. Método DECA SUGERENCIA DE TEMPORALIZACIÓN Enero MarzoFebrero ES0000000024590 663006_Matematicas_4_GRAZ_24259 PRIMARIA PRIMARIA Matemáticas PRIMARIA ANDALUCÍAMatemáticas ANDALUCÍA Matemáticas ANDALUCÍA ES0000 000024 590 663006 _Matem aticas_4_GRA Z_2425 9.indd 1 04/03/2 015 11:21:19 ES0000000024593 663039_Cdno_Matematicas_4-2_22732 PRIMARIA Matemáticas Segundo trimestre Matemáticas Segundo trimestre PRIMARIA CUADERNO CUADERNO ES0000000024593 663039_Cdno_Matematicas_4-2_22732.indd 1 19/02/2015 16:56:18 25
  • 26.
    7 Números decimales Cadaaño más altos Los alumnos de 4.º, desde que iban a Infantil, miden su altura cada año a mitad de curso. Forman grupos de tres y con la cinta métrica se miden unos a otros. En una tabla van anotando las alturas en metros de cada uno. Desde hace tiempo, todos miden 1 metro y muchos centímetros. ¡Algunos quizá lleguen a medir 2 metros de altura! Altura en metros Ana 1 m y 30 cm Carlos 1 m y 26 cm Asun 1 m y 35 cm Ernesto 1 m y 32 cm Julián 1 m y 29 cm 98 ES0000000024590 663006-Unidad 07_22590.indd 98 10/03/2015 13:16:50 Propósitos •  Reconocer situaciones reales en las que se utilicen números decimales. •  Recordar los conceptos básicos necesarios para el desarrollo de la unidad. Previsión de dificultades •  Algunos alumnos pueden tener dificultad en la lectura y escritura   de números decimales cuando   la primera o las dos primeras cifras decimales son cero. Realice actividades de lectura y escritura de números decimales para subsanar estas posibles dificultades. •  Las aproximaciones de decimales plantean en ocasiones dificultades   a los alumnos. Muestre la similitud con el proceso seguido en   los números naturales. Trabajo colectivo sobre la lámina Pida a un alumno que lea la lectura   y pregúnteles si ellos se han medido  alguna vez, si saben cuánto miden, cuál es esa medida, etc.   A continuación, hágales observar la tabla y pregunte a la clase si conocen otra forma de expresar esas estaturas.  Si los alumnos no la aportan, señale que existe otra manera, utilizando los números decimales. Comente que en esta unidad van a trabajar con estos números y que aprenderán muchas cosas sobre ellos. 1 Ana mide 1 m y 30 cm.   Es más alta que Carlos.  Hay 4 cm de diferencia.  La que mide más es Asun y   el que mide menos Carlos. 2 Carlos: 1,26 m.   Asun: 1,35 m.  Ernesto: 1,32 m.   Julián: 1,29 m. 3 R. M. Puede medir 1,27 m   o 1,28 m. También cualquier  otro decimal comprendido entre 1,26 y 1,29. Otras formas de empezar •  Pida a los alumnos que traigan a clase folletos publicitarios, revistas, periódicos…, y que busquen en ellos contextos en los que aparezcan números decimales. Comente con ellos algunos casos. Después, pregúnteles si saben cuál de los números es mayor o menor   y que expliquen por qué. •  Pregunte a los alumnos que si conocen situaciones en las que se utilizan números decimales y pídales que las enumeren. Propóngales que digan por qué creen que son necesarios en esas situaciones los números decimales. 26
  • 27.
    ¿Qué sabes ya? 1¿Cuánto mide Ana? ¿Es más alta que Carlos? ¿Cuántos centímetros hay de diferencia entre ellos? De los cinco alumnos, ¿quién es el que mide más? ¿Y menos? 2 Si escribimos la altura de Ana como 1,30 m, ¿cómo escribirías la altura de los demás alumnos? ¿Cómo se escribiría la altura del más alto? 3 EXPRESIÓN ORAL. ¿Cuánto puede medir Lidia si mide más que Carlos y menos que Julián? Da varias posibilidades. Lee, comprende y razona Fracciones de denominador 10 – Denominador: cada figura está dividida en 10 partes iguales. – Numerador: número de partes coloreadas en cada figura. 2 10 5 10 8 10 dos décimos cinco décimos ocho décimos 1 Escribe cada fracción representada y cómo se lee. 2 Dibuja en tu cuaderno y representa estas fracciones. 3 10 7 10 Un décimo. Seis décimos. 3 Observa las figuras pintadas de cada color y completa en tu cuaderno como en el ejemplo. TAREA FINAL Estudiar la evolución de un precio Al final de la unidad analizarás los cambios de un precio. Antes, trabajarás con los números decimales, los compararás y aproximarás. SABER HACER EJEMPLO … figuras y ... 10 de otra. 99 ES0000000024590 663006-Unidad 07_22590.indd 99 10/03/2015 13:16:51 UNIDAD 7 ¿Qué sabes ya? Repase con los alumnos los conceptos relacionados con las fracciones de denominador 10: lectura, escritura, representación..., ya que están muy relacionados con las décimas, las primeras unidades decimales que estudiarán en la unidad. 1 •  4 10 . Cuatro décimos. •  5 10 . Cinco décimos. •  9 10 . Nueve décimos. 2 R. L. 3 •  2 figuras y 2 10 de otra. •  3 figuras y 6 10 de otra. Notas Competencias •  Comunicación lingüística. Al realizar las actividades propuestas después de la lectura, es importante que los alumnos conozcan y utilicen el lenguaje matemático correctamente para expresarse. •  Aprender a aprender. Exprese a los alumnos la importancia que tiene afianzar y reforzar los conocimientos para poder avanzar sin dificultad. Recuérdeles cómo se representan las unidades decimales, así como su expresión en forma de fracción y en forma decimal. Inteligencia lingüística 27
  • 28.
    Unidades decimales 1 Escribeen forma de fracción y en forma de número decimal. 3 décimas 8 centésimas 4 milésimas 5 décimas 5 centésimas 7 milésimas 7 décimas 12 centésimas 92 milésimas 9 décimas 39 centésimas 214 milésimas 2 Copia la tabla en tu cuaderno y complétala. Las unidades decimales se obtienen al dividir la unidad en partes iguales. Se pueden expresar como fracción o como número decimal. Si la unidad se divide en 10 partes iguales, cada parte es 1 décima. 1 unidad 5 10 décimas 1 10 5 0,1 fracción decimal Si la unidad se divide en 100 partes iguales, cada parte es 1 centésima. 1 unidad 5 100 centésimas 1 100 5 0,01 fracción decimal Si la unidad se divide en 1.000 partes iguales, cada parte es una milésima. 1 unidad 5 1.000 milésimas 1 1.000 5 0,001 EJEMPLO 3 décimas 5 3 10 5 0,3 Unidades decimales 18 centésimas 39 milésimas Forma de fracción 7 10 713 1.000 Forma decimal 0,18 0,65 Las equivalencias entre la unidad y las unidades decimales son: 1 unidad 5 10 décimas 5 100 centésimas 5 1.000 milésimas 1 décima 5 10 centésimas 1 centésima 5 10 milésimas 100 ES0000000024590 663006-Unidad 07_22590.indd 100 10/03/2015 13:16:52 Propósitos •  Reconocer las unidades decimales. •  Conocer y aplicar las relaciones entre unidades decimales. Sugerencias didácticas Para explicar. Haga que los alumnos observen el cuadro informativo y explique el significado de décima, centésima y milésima. Escriba en la pizarra cómo se expresan en forma de fracción y en forma decimal. Comente las equivalencias entre las distintas unidades decimales. Para reforzar. Prepare tarjetas de cartulina iguales y escriba en algunas de ellas unidades decimales, en otras sus expresiones como fracción, en otras como decimal y en otras su representación. Coloque las tarjetas con dibujos en fila en el corcho y ponga las demás tarjetas en su mesa, mezcladas y boca abajo. Pida a los alumnos que, por orden, cojan una tarjeta, digan qué unidad es y la coloquen debajo del dibujo correspondiente. Actividades 1   •  3 10 5 0,3 •  5 10 5 0,5 •  7 10 5 0,7 •  9 10 5 0,9 •  8 100 5 0,08 •  5 100 5 0,05 •  12 100 5 0,12 •  39 100 5 0,39 •  4 1.000 5 0,004 •  7 1.000 5 0,007 •  92 1.000 5 0,092 •  214 1.000 5 0,214 2   18 centésimas 5 18 100 5 0,18 7 décimas 5 7 10 5 0,7 65 centésimas 5 65 100 5 0,65 Otras actividades •  Proponga a los alumnos un dictado de unidades decimales. Nombre varias décimas, centésimas o milésimas para que los alumnos escriban en forma de fracción y en forma decimal. Después pida   a un alumno que escriba en la pizarra sus resultados y entre todos   se comprobará si los resultados son o no correctos. Ejemplo: 3 décimas 24 centésimas 934 milésimas 5 décimas 8 centésimas 76 milésimas 28
  • 29.
    Problemas 5 Resuelve. Marta hahecho un mosaico de 100 piezas. – ¿Cuántas centésimas son de color rojo? – ¿Cuántas centésimas son de color amarillo? ¿A cuántas décimas equivalen? – ¿Cuántas centésimas son de color verde? ¿A cuántas décimas y centésimas equivalen? Una parcela ha sido dividida en 1.000 partes iguales y han sembrado 350 de ellas. ¿Cuántas milésimas han sembrado? ¿Cuántas no han sido sembradas? 7 3 Completa en tu cuaderno. Usa las equivalencias. 3 unidades 5 … décimas 7 unidades 5 … décimas 9 unidades 5 … décimas 5 décimas 5 … centésimas 7 décimas 5 … centésimas 8 décimas 5 … centésimas 6 centésimas 5 … milésimas 7 centésimas 5 … milésimas 9 centésimas 5 … milésimas 4 Expresa en la unidad indicada. 2 unidades y 7 décimas 4 unidades y 5 décimas 5 unidades y 2 décimas 6 unidades y 9 décimas 5 unidades y 1 centésima 9 décimas y 8 centésimas 5 unidades y 86 centésimas 4 décimas y 5 centésimas 8 unidades y 4 milésimas 6 centésimas y 25 milésimas 7 unidades y 834 milésimas 2 centésimas y 18 milésimas Problemas 5 Resuelve. Marta ha hecho un mosaico de 100 piezas. – ¿Cuántas centésimas son de color rojo? – ¿Cuántas centésimas son de color amarillo? ¿A cuántas décimas equivalen? – ¿Cuántas centésimas son de color verde? ¿A cuántas décimas y centésimas equivalen? Una parcela ha sido dividida en 1.000 partes iguales y han sembrado 350 de ellas. ¿Cuántas milésimas han sembrado? ¿Cuántas no han sido sembradas? Halla la mitad de decenas y de centenas CÁLCULO MENTAL EJEMPLO 2 unidades y 7 décimas 5 20 décimas 1 7 décimas 5 27 décimas 10 : 2 60 : 2 20 : 2 70 : 2 40 : 2 80 : 2 50 : 2 90 : 2 30 : 2 5 15 100 : 2 600 : 2 200 : 2 700 : 2 300 : 2 800 : 2 400 : 2 900 : 2 500 : 2 5 250 En décimas En centésimas En milésimas 101 ES0000000024590 663006-Unidad 07_22590.indd 101 10/03/2015 13:16:55 UNIDAD 7 39 milésimas 5 39 1.000 5 0,039 713 milésimas 5 713 1.000 5 0,713 3   3 unidades 5 30 décimas 7 unidades 5 70 décimas 9 unidades 5 90 décimas 5 décimas 5 50 centésimas 7 décimas 5 70 centésimas 8 décimas 5 80 centésimas 6 centésimas 5 60 milésimas 7 centésimas 5 70 milésimas 9 centésimas 5 90 milésimas 4   •  27 décimas • 45 décimas •  52 décimas • 69 décimas •  501 centésimas •  586 centésimas •  98 centésimas •  45 centésimas •  8.004 milésimas •  7.834 milésimas •  85 milésimas •  38 milésimas 5   •  Rojo: 8 centésimas. Amarillo: 10 centésimas 5 5 1 décima. Verde: 37 centésimas 5 5 3 décimas y 7 centésimas. • Han sembrado 350 milésimas. 1.000 2 850 5 150 No han sembrado 150 milésimas. Cálculo mental • 5 • 30 • 50 • 300 • 10 • 35 • 100 • 350 • 20 • 40 • 150 • 400 • 25 • 45 • 200 • 450 Notas Competencias • Conciencia y expresión cultural. La realización de dibujos similares al de la actividad 5 permite, por un lado, potenciar la competencia artística y creativa de los alumnos a la vez que, a partir de los dibujos producidos, trabajan los contenidos de esta doble página. Pídales a los alumnos que en una cuadrícula 10 3 10 realicen un dibujo artístico con colores y después trabaje con ellos qué parte es de color, cómo se lee ese número decimal, a qué otras unidades decimales equivale… 29
  • 30.
    Números decimales 1 Escribeen tu cuaderno cada número decimal representado. Después, indica cuál es su parte entera y su parte decimal. 2 Escribe un número decimal. Cuya parte entera sea 5. Cuya parte decimal sea 8 décimas. Cuya parte decimal sea 15 centésimas. Cuya parte decimal sea 392 milésimas. Laura está participando en un campeonato de gimnasia. En una de las pruebas ha obtenido 38,752 puntos. El número 38,752 es un número decimal. Un número decimal tiene dos partes, separadas por una coma: Lectura. Los números decimales se pueden leer de dos formas. 38,752 38 coma 752 38 unidades y 752 milésimas Descomposición. 38,752 5 3 decenas 1 8 unidades 1 7 décimas 1 5 centésimas 1 2 milésimas 38,752 5 30 1 8 1 0,7 1 0,05 1 0,002 Los números decimales tienen dos partes: – La parte entera (unidades, decenas, centenas…) a la izquierda de la coma. – La parte decimal (décimas, centésimas, milésimas…) a la derecha de la coma. Parte entera Parte decimal Decenas D Unidades U décimas d centésimas c milésimas m 3 8 , 7 5 2 EJEMPLO 1,7 Parte entera: … Parte decimal: … 102 ES0000000024590 663006-Unidad 07_22590.indd 102 10/03/2015 13:16:57 Propósitos •  Descomponer, leer y escribir números decimales. •  Usar los números decimales   en situaciones reales. Sugerencias didácticas Para explicar. Haga que un alumno lea la situación planteada y escriba en la pizarra el número decimal correspondiente. Comente cuál es su parte entera y decimal, cómo se descompone en sus órdenes y en forma de suma, cuáles son las dos formas de leerlo… Escriba en la pizarra otros casos similares y realice en común estos procedimientos. Muestre la similitud con los procedimientos seguidos con los números naturales y llame la atención sobre la importancia del valor posicional de las cifras. Trabaje en especial algunos casos   de números con ceros intermedios, que tienen mayor dificultad. Actividades 1 •  1,7 Parte entera: 1.  Parte decimal: 7. •  1,013 Parte entera: 1.  Parte decimal: 013. •  3,036 Parte entera: 3.  Parte decimal: 036. 2 R. M. •  5,9 •  4,8 •  3,15 •  1,392 3 •  R. M. 2 unidades y 7 décimas  2 coma 7 •  19 unidades y 36 centésimas •  8 unidades y 123 milésimas •  7 unidades y 68 centésimas •  25 unidades y 3 décimas •  6 unidades y 3 milésimas •  690 unidades y 42 centésimas •  9 unidades y 17 milésimas •  48 unidades y 902 milésimas •  16 unidades y 2 centésimas 4 •  5,4 •  17,9 •  21,37 •  236,08 •  71,008 •  56,042 Otras actividades •  Pida a los alumnos que, durante una semana, busquen y copien varios números decimales que vean en lugares fuera de la clase.   Después, trabaje esos números en común, anotando en qué lugar   los han encontrado, cuál es su escritura, su descomposición,   el valor posicional de sus cifras... 30
  • 31.
    7 Piensa y contesta. ¿Entrequé números naturales está comprendido 3,76? ¿Existen números decimales comprendidos entre 8,4 y 8,5? Pon dos ejemplos si crees que sí. ¿Existen números decimales entre 9,27 y 9,28? Pon dos ejemplos si crees que sí. RAZONAMIENTO 3 Escribe de dos formas cómo se lee cada número. 2,7 8,123 25,3 690,42 48,902 19,36 7,68 6,003 9,017 16,02 4 Escribe con cifras cada número decimal. 5 coma 4 17 unidades y 9 décimas 21 coma 37 236 unidades y 8 centésimas 71 coma 008 56 unidades y 42 milésimas 5 Escribe el valor de la cifra 5 en cada número. 28,15 26,015 52,301 7 coma 05 25 coma 937 8 coma 105 6 Descompón cada número. 8,3 4,825 12,609 79,8 9,76 7,34 25,06 210,094 Problemas 7 Resuelve. Expresa el resultado con un número decimal. Marcos tardó 13 segundos y 15 centésimas en correr 100 metros. Leonor tardó 26 centésimas más. ¿Cuánto tardó Leonor? Marisa tenía 25 euros y 70 céntimos. Compró un pantalón por 13 euros y 25 céntimos. ¿Cuánto dinero le quedó? EJEMPLO 28,15 5 centésimas 5 0,05 103 ES0000000024590 663006-Unidad 07_22590.indd 103 10/03/2015 13:16:58 UNIDAD 7 5 • 5 centésimas 5 0,05 • 5 milésimas 5 0,005 • 5 decenas 5 50 unidades • 5 centésimas 5 0,05 • 5 unidades 5 5 • 5 milésimas 5 0,005 6 • 8 U 1 3 d 5 8 1 0,3 • 9 U 1 7 d 1 6 c 5 5 9 1 0,7 1 0,06 • 4 U 1 8 d 1 2 c 1 5 m 5 5 4 1 0,8 1 0,02 1 0,005 • 7 U 1 3 d 1 4 c 5 5 7 1 0,3 1 0,04 • 1 D 1 2 U 1 6 d 1 9 m 5 5 10 1 2 1 0,6 1 0,009 • 2 D 1 5 U 1 6 c 5 5 20 1 5 1 0,06 • 7 D 1 9 U 1 8 d 5 5 70 1 9 1 0,8 • 2 C 1 1 D 1 9 c 1 4 m 5 5 200 1 10 1 0,09 1 0,004 7 • Marcos: 13,15 s. 15 1 26 5 41 Leonor: 13,41 s. Leonor tardó 13,41 segundos. • Marisa: 25,70 €. 25 2 13 5 12 70 2 25 5 45 Le quedaron 12,45 €. Razonamiento • Entre 3 y 4. • Sí, existen infinitos números decimales. Por ejemplo: 8,41, 8,412... • Sí, existen infinitos números decimales. Por ejemplo: 8,271, 8,272... Notas Otras actividades • Realice actividades de paso de unas expresiones a otras para potenciar la comprensión de los números decimales. Enuncie o escriba una de las expresiones posibles (con cifras, con letras de una de las dos formas, descompuesta en forma de suma, descompuesta en sus órdenes…) y pida a los alumnos que determinen todas las otras. • Escriba varias expresiones de números decimales en la pizarra. Los alumnos deberán determinar cuáles de ellas corresponden a un mismo número decimal. Aproveche para trabajar los números con ceros ya que suelen plantear especiales dificultades. 31
  • 32.
    Comparación de númerosdecimales 1 Copia los números en tu cuaderno y rodea. 6,75 y 9,13 9,036 y 9,032 27,34 y 27,61 18,35 y 18,62 8,4 y 8,399 6,45 y 7,1 28,16 y 28,09 39,106 y 39,2 2 Ordena cada grupo de números como se indica. Usa el signo correspondiente. El modelo Veloz ha tardado 19,638 segundos en recorrer el circuito, mientras que el modelo Rayo ha tardado 19,64 segundos. ¿Cuál ha tardado menos? Compara 19,638 y 19,64 1.º Compara las partes enteras. 19,638 19,64 2.º Como las partes enteras son iguales, compara las décimas. 19,638 19,64 3.º Como las décimas son iguales, compara las centésimas. 19,638 19,64 Luego 19,638 , 19,64. Ha tardado menos el modelo Veloz. Al comparar números decimales, primero se comparan las partes enteras. Si son iguales, se comparan las décimas, centésimas, milésimas… 19 5 19 6 5 6 3 , 4 El número mayor El número menor 3 Escribe tres números mayores que 4 cuya parte decimal sea menor que 75. De menor a mayor De mayor a menor 3,6 3,59 3,475 7,9 7,84 7,82 2,83 2,834 2,9 2,87 8,15 8,2 8,179 9,5 9,52 9,253 12,34 12,39 12,4 12,397 104 ES0000000024590 663006-Unidad 07_22590.indd 104 10/03/2015 13:16:59 Propósitos •  Comparar números decimales. •  Ordenar series de números decimales de menor a mayor   o viceversa. Sugerencias didácticas Para explicar. Lea la situación planteada y escriba en la pizarra los dos números decimales. Pregunte   a los alumnos qué procedimiento seguían para comparar dos números naturales. Una vez recordado, explique el procedimiento que hay que seguir para comparar dos números decimales. Indique las similitudes entre ambos, comentando que para comparar decimales hay que comparar primero sus partes enteras, que son números naturales. Deje claro que un número decimal con menos cifras que otro no tiene por qué ser menor que él (error común). Actividades 1 •  9,13 •  9,036 •  27,61 •  18,62 •  8,399 •  6,45 •  28,09 •  39,106 2 •  3,475 , 3,59 , 3,6 •  7,82 , 7,84 , 7,9 •  2,83 , 2,834 , 2,87 , 2,9 •  8,2 . 8,179 . 8,15 •  9,52 . 9,5 . 9,253 •  12,4 . 12,397 . 12,39 . 12,34 Notas Otras actividades •  Pida a los alumnos que escriban un número decimal en un folio que cumpla una cierta condición dada por usted (por ejemplo: su parte entera es 12;   está comprendido entre 3 y 4; tiene dos cifras decimales…). Después, saque a varios a la pizarra y pídales que viendo sus números se ordenen de menor a mayor o de mayor a menor. Cuando lo hayan hecho, la clase determinará   si su ordenación es correcta o no.  Una vez establecido el orden, pida a un alumno que diga un número decimal comprendido entre dos de los números, entre qué naturales está uno   de los decimales, un número decimal mayor que el más grande de   los escritos que tenga su misma parte entera o decimal… 32
  • 33.
    7Aproximación de númerosdecimales Fíjate en cómo se aproximan estos números decimales. ¿Cómo se aproxima 3,7 a las unidades? 1.º Busca entre qué unidades está. Está entre 3 y 4. 2.º Elige la unidad más próxima. Para ello compara la cifra de las décimas con 5. 7 . 5 La aproximación a las unidades es 4. ¿Cómo se aproxima 9,481 a las centésimas? 1.º Busca entre qué centésimas está. Está entre 9,48 y 9,49. 2.º Elige la centésima más próxima. Para ello compara la cifra de las milésimas con 5. 1 , 5 La aproximación a las centésimas es 9,48. 3,7 4 7 . 5 3 1 1 5 4 9,481 9,48 1 , 5 8 5 8 3 3,43,2 3,6 3,93,1 3,5 3,83,3 3,7 4 9,48 9,481 9,4859,483 9,487 9,4899,482 9,4869,484 9,488 9,49 1 Aproxima cada número decimal al orden indicado. 6,4 7,2 8,8 9,3 11,6 21,7 8,72 5,49 7,18 10,11 25,63 42,91 0,726 8,124 9,017 4,777 4,771 19,818 2 Escribe dos números decimales cuya aproximación a las décimas sea 8,4. A las unidades A las décimas A las centésimas Halla la mitad de números de 2 y de 3 cifras (todas pares) CÁLCULO MENTAL 48 : 2 68 : 2 24 : 2 84 : 2 26 : 2 88 : 2 64 : 2 5 32 486 : 2 5 243 242 : 2 688 : 2 426 : 2 846 : 2 468 : 2 864 : 2 105 ES0000000024590 663006-Unidad 07_22590.indd 105 10/03/2015 13:17:00 UNIDAD 7 Propósitos •  Aproximar números decimales a las unidades, décimas y centésimas. Sugerencias didácticas Para empezar. Realice actividades de aproximación de números naturales. Para explicar. Muestre la similitud con el trabajo realizado al aproximar los números naturales. Deje claro que el número decimal obtenido en cada caso será un número natural,   un número con una cifra decimal   o un número con dos cifras decimales. En este curso hemos aproximado cada número al orden inmediatamente menor que él. Puede extender el trabajo a aproximaciones a órdenes menores (un número   de tres cifras decimales a las décimas o unidades) si lo cree conveniente. Actividades 1 •  6 7 9 9 12 22 •  8,7 5,5 7,2 10,1 25,6 42,9 •  0,73 8,12 9,02     4,78 4,77 19,82 2 R. M. 8,43        8,42        8,39        8,37 Cálculo mental • 24 • 34 • 121 • 344 • 12 • 42 • 213 • 423 • 13 • 44 • 234 • 432 Notas Otras actividades • Utilizando las tarjetas con números decimales realizadas en el apartado Otras actividades de la página anterior, pida a distintos alumnos   que salgan a la pizarra y trabajen las aproximaciones. Por ejemplo, pida  a cada uno de ellos que aproxime al orden inmediatamente menor   su número. La clase comprobará si su respuesta es correcta o no.  Después, pida a todos que digan dos números cuya aproximación  a ese orden sea la misma que la de ese número. Inteligencia espacial 33
  • 34.
    Escribe cada problemacolocando los datos en el lugar adecuado. Después, resuelve. 1 A la peluquería fueron el viernes 28 personas. De ellas, 10 eran mujeres, 45 hombres (algunos menos que mujeres) y el resto niños. ¿Cuántos niños fueron a la peluquería? 2 Juan pesa 5 kg, su hermano Raúl 20 kg menos que él, y su hermana Rosa, la más pequeña, pesa 48 kg menos que Raúl. ¿Cuántos kilos pesan los tres juntos? 3 Marta tenía 370 billetes de 18 € y 20 € en monedas. Ha comprado una cámara fotográfica de 15 €. ¿Cuánto dinero le ha sobrado? 4 En el almacén han envasado 5 kg de patatas. La mitad la han puesto en bolsas de 400 kg y el resto, en bolsas el doble de grandes, de 70 kg cada una. ¿Han obtenido más de 10 bolsas? Lee el problema y escríbelo de nuevo poniendo los datos en su lugar correspondiente. Después, revísalo y resuélvelo en tu cuaderno. En la fábrica trabajan 400 días de los 340 días de cada año. Cada día envasan 13 botes, que venden a 365 € cada uno. ¿Cuánto dinero obtienen al año por la venta? Al leer el problema vemos que hay datos mal colocados. Un año no tiene 340 días ni se pueden trabajar 400 días en un año. El problema con los datos bien colocados queda así: En la fábrica trabajan 340 días de los 365 días de cada año. Cada día envasan 400 botes, que venden a 13 € cada uno. ¿Cuánto dinero obtienen al año por la venta? Resuelve el problema en tu cuaderno. Ordenar los datos de un problema Solución de problemas 106 ES0000000024590 663006-Unidad 07_22590.indd 106 10/03/2015 13:17:01 Propósitos •  Ordenar los datos de un problema   y resolverlo. •  Ordenar los datos de un problema   e inventar una pregunta. Sugerencias didácticas Para explicar. Haga que los alumnos lean el problema y explíqueles que   los datos de este problema están desordenados y que debemos colocarlos en su lugar correspondiente. Deles un tiempo para pensar y, después, vaya razonando en común en qué lugar debe quedar cada dato. Muestre la importancia de analizar, una vez cambiados de lugar los datos, si el problema tiene sentido. Actividades 1   A la peluquería fueron el viernes 45 personas. De ellas 28 eran mujeres, 10 hombres (algunos menos que mujeres) y el resto niños. ¿Cuántos niños fueron a la peluquería?   45 2 28 2 10 5 45 2 38 5 7  A la peluquería fueron 7 niños. 2   Juan pesa 48 kg, su hermano Raúl 5 kg menos que él, y su hermana Rosa, la más pequeña, pesa 20 kg menos que Raúl. ¿Cuántos kilos pesan los tres juntos? 48 1 43 1 23 5 114  Los tres juntos pesan 114 kg. 3   Marta tenía 18 billetes de 20 €   y 15 € en monedas. Ha comprado una cámara fotográfica de 370 €. ¿Cuánto dinero le ha sobrado? 18 3 20 1 15 5 375  375 2 370 5 5  Le han sobrado 5 €. 4   En un almacén han envasado   400 kg de patatas. La mitad la han puesto en bolsas de 5 kg y el resto en bolsas el doble de grandes, de 10 kg cada una. ¿Han obtenido más de 70 bolsas?  (400 : 2) : 5 5 40; 200 : 10 5 20 40 1 20 5 60  No, han obtenido 60 bolsas. Otras actividades •  Forme grupos de 4 alumnos y pida a dos de ellos que inventen y escriban   un problema. Después, en otra hoja, lo reescribirán con los datos desordenados y se lo plantearán a los otros componentes del grupo   para que coloquen los datos en el lugar correspondiente y lo resuelvan.   Más tarde, cada grupo comprobará el desempeño del otro. A continuación, haga una puesta en común con las propuestas dadas   por los distintos grupos y resuelva algunos de los problemas propuestos   de forma colectiva. 34
  • 35.
    Coloca los datosen el lugar adecuado e inventa una pregunta que se resuelva usando todos ellos. Después, resuélvela. 7 Coloca los datos en el lugar correcto e inventa los datos que faltan. Después, resuelve cada problema. 5 Marcos tiene que llevar en su furgoneta cuatro paquetes. El rojo es el más ligero, pesa 98 kg, el verde pesa más que él, y más aún pesan el azul y el morado, que pesan 85 kg. ¿Cuántos kilos pesan todos juntos? 6 Mónica ha comprado 3 kg de peras a 16 € el kilo y el doble de kg de manzanas, a 4 € el kg. El kilo de manzanas es más barato que el de peras. ¿Cuánto le han costado las manzanas más que las peras? 7 Jaime tenía varias monedas de 28 € y 20 billetes de 2 €. Compró un pantalón por 3 €, y un libro más barato que el pantalón. ¿Cuánto dinero le sobró? 8 La familia Sánchez ha ido al teatro. Han ido 12 adultos, 4 de ellos jubilados, y el triple de niños que de adultos, 5. La entrada de jubilado cuesta 3 €, la de niño cuesta un poco más y la de adulto es la más cara. ¿Cuánto han pagado por todas las entradas? INVENTA TUS PROBLEMAS Coloca los datos en el lugar adecuado e inventa una pregunta que se resuelva usando todos ellos. Después, resuélvela. Silvia mide 80 cm y su hermano pequeño mide 145 cm menos que ella. Micaela entrenó durante tres días. El primero entrenó menos, 45 minutos; el segundo algo más, 29 minutos, y el tercero aún más, 32 minutos. César preparó 35 bandejas de pasteles. En cada una había 3 pasteles de fresa y algunos más de chocolate. En total en cada bandeja había 15 pasteles. 1 2 3 107 ES0000000024590 663006-Unidad 07_22590.indd 107 10/03/2015 13:17:02 UNIDAD 7 5   R. M. Marcos tiene que llevar en su furgoneta cuatro paquetes. El rojo es el más ligero, pesa 85 kg, el verde pesa 88 kg y el azul y el morado pesan 98 kg. ¿Cuántos kilos pesan juntos? 85 1 88 1 2 3 98 5 369 Pesan 369 kg. 6   R. M. Mónica ha comprado 16 kg de peras a 4 € el kilo y el doble de kilos de manzanas, a 3 € el kilo. ¿Cuánto le han costado las manzanas más que las peras? 16 3 4 5 64; 16 3 2 3 3 5 96 96 2 64 5 32 Han costado 32 € más. 7   R. M. Jaime tenía 4 monedas de 2 € y 3 billetes de 20 €. Compró un pantalón por 28 € y un libro por 19 €. ¿Cuánto dinero le sobró? 4 3 2 1 3 3 20 5 68 68 2 (28 1 19) 5 21 Le sobraron 21 €. 8   R. M. La familia Sánchez ha ido al teatro. Han ido 4 adultos, 3 de ellos jubilados, y el triple de niños que de adultos, 12. La entrada de jubilado cuesta 5 €, la de niño 6 € y la de adulto 10 €. ¿Cuánto han pagado por las entradas? 1 3 10 1 3 3 5 1 12 3 6 5 97 Han pagado 97 €. Inventa tus problemas 1   R. M. Silvia mide 145 cm y su hermano pequeño mide 80 cm menos que ella. ¿Cuántos centímetros mide Silvia más que su hermano? Mide 65 cm más. 2   R. M. Micaela entrenó durante tres días. El primer día entrenó menos, 29 minutos, el segundo día más, 32 minutos y el tercer día aún más, 45 minutos. ¿Cuánto tiempo entrenó? Entrenó 106 minutos. 3   R. M. César preparó 3 bandejas de pasteles. En cada bandeja había 15 pasteles de fresa y algunos más de chocolate. En cada bandeja había 35 pasteles. ¿Cuántos pasteles de chocolate había? Había 60 pasteles de chocolate. Competencias •  Iniciativa y emprendimiento. Las actividades de invención de problemas son un contexto que permite a los alumnos profundizar en el desarrollo de esta competencia. Pida a los alumnos que a la hora de inventar preguntas sean lo más creativos posible y que no olviden comprobar la corrección del problema planteado. 35
  • 36.
    6 Escribe dedos formas cómo se lee cada número. 1,4 9,37 15,304 0,8 8,06 31,008 7 Escribe con cifras. 2 unidades y 9 centésimas 3 unidades y 28 milésimas 15 unidades y 7 décimas 20 unidades y 106 milésimas 8 Descompón cada número decimal. 3,9 6,504 28,003 2,17 12,03 145,207 9 ¿Qué número es? Escribe. 2 unidades 1 4 décimas 3 unidades 1 2 centésimas 8 décimas 1 6 milésimas 3 unidades 1 2 décimas 1 1 milésima 10 VOCABULARIO. Explica cómo se comparan dos números decimales. Ayúdate con un ejemplo. 11 Compara. 3,5 y 3,49 2,704 y 2,706 8,004 y 8,1 9,4 y 9,402 6,72 y 6,719 4,999 y 4,996 12 Aproxima cada número al orden indicado. A las unidades: 9,4 6,8 6,9 7,1 A las décimas: 6,73 2,91 8,39 4,06 A las centésimas: 3,676 2,119 8,462 1 Expresa la parte coloreada como fracción y como número decimal. 2 Expresa como número decimal. 4 décimas 28 centésimas 275 milésimas 3 milésimas 3 10 29 100 37 1.000 5 100 145 1.000 7 1.000 3 Utiliza las equivalencias y expresa en la unidad indicada. En décimas 4 unidades 6 unidades 2 unidades y 4 décimas En centésimas 3 unidades 5 unidades 4 unidades y 25 centésimas En milésimas 7 unidades 8 unidades 5 unidades y 125 milésimas 4 Copia en tu cuaderno y rodea de rojo la parte entera y de verde, la decimal. 1,4 9,057 65,102 37,82 8,31 316,04 5 Expresa cada precio como un número decimal. 5 € y 21 céntimos 6 céntimos 4 € y 2 céntimos 14 céntimos 28 € y 50 céntimos 70 céntimos ACTIVIDADES 108 ES0000000024590 663006-Unidad 07_22590.indd 108 10/03/2015 13:17:03 Propósitos •  Repasar los contenidos básicos   de la unidad. Actividades 1   •  7 10           •  6 100           •  57 100 2   •  0,4 •  0,28 •  0,275 •  0,003 •  0,3 •  0,29 •  0,037 •  0,05 •  0,145 •  0,007 3   •  40 décimas           •  60 décimas •  24 décimas •  300 centésimas •  500 centésimas •  425 centésimas •  7.000 milésimas •  8.000 milésimas •  5.125 milésimas 4   •  1 •  9 •  65 4 057 102 •  37 •  8 •  316 82 31 04 5   •  5,21 € •  0,06 € •  4,02 € •  0,14 € •  28,50 € •  0,70 € 6   •  R. M. 1 unidad y 4 décimas  1 coma 4 •  8 décimas •  9 unidades y 37 centésimas •  8 unidades y 6 centésimas •  15 unidades y 304 milésimas •  31 unidades y 8 milésimas 7   •  2,09 •  15,7 •  3,028 •  20,106 8   •  3 U 1 9 d 5 3 1 0,9 •  2 U 1 1 d 1 7 c 5   5 2 1 0,1 1 0,07 •  6 U 1 5 d 1 4 m 5   5 6 1 0,5 1 0,004 •  1 D 1 2 U 1 3 c 5  5 10 1 2 1 0,03 •  2 D 1 8 U 1 3 m 5  5 20 1 8 1 0,003 •  1 C 1 4 D 1 5 U 1 2 d 1 7 m 5 5 100 1 40 1 5 1 0,2 1 0,007 Otras actividades •  Escriba en la pizarra varios números decimales escritos de distintas formas. Por ejemplo: 5,087              3 unidades y 9 centésimas 3 unidades 1 5 décimas 1 8 milésimas            3 1 0,7 1 0,002 Pídales que se fijen en un número y haga que escriban su expresión   con cifras o letras, su descomposición o su lectura. También puede pedirles que los ordenen de menor a mayor. 36
  • 37.
    BA C Problemas 13 Resuelve. Elmodelo A ha gastado 6,9 litros en recorrer 100 km, el modelo B 6,85 litros y el C ha gastado más que el B pero menos que el A. ¿Cuánto ha podido gastar el modelo C? Carlos tenía 2 monedas de 2 €, 1 moneda de 10 céntimos y 3 monedas de 2 céntimos. ¿Puede comprar un cuaderno que cuesta 4,15 €? 14 Resuelve. Lara ha tardado en nadar una distancia 2 minutos y 9 décimas; José, 2 minutos y 9 milésimas, y Olga, 2 minutos y 9 centésimas. ¿Quién ha llegado el primero a la meta? David ha saltado 6,7 m de longitud y Lidia 5,2 m. ¿Cuántos metros ha saltado aproximadamente cada uno? Miguel ha comprado un pantalón por 35,62 €, una camisa por 17,26 € y un abrigo por 80,19 €. ¿Cuánto cuesta aproximadamente cada prenda? 15 Observa la tabla y resuelve. Observa las temperaturas máximas y mínimas en grados centígrados de varias localidades en un año. ¿Qué lugar tuvo la temperatura máxima más alta? ¿Y la mínima más baja? Luisa quiere ir a veranear a un lugar que tuviera menos de 36 ºC de máxima. ¿A cuáles podrá ir? Pedro quiere ir en invierno a un lugar que tuviera más de 1 ºC de mínima. ¿A cuáles podrá ir? 7 16 Ordena de menor a mayor estos números. ¿Cómo lo haces? 0,7 71 100 0,69 695 1.000 Demuestra tu talento Lugar Villares Valverde Cerrillo Cobijo Máxima 32,5 34,9 37,8 33,8 Mínima 1,6 0,5 1,2 0,9 109 ES0000000024590 663006-Unidad 07_22590.indd 109 10/03/2015 13:17:04 UNIDAD 7 9   •  2,4 •  0,806 •  3,02 •  3,201 10  R. L. 11  •  3,5 . 3,49 •  2,704 , 2,706 •  8,004 , 8,1 •  9,4 , 9,402 •  6,72 . 6,719 •  4,999 . 4,996 12  •  9  7  7  7 •  6,7 2,9 8,4 4,1 •  3,68  2,12  8,46 13  •  Ha podido gastar 6,86 ℓ; 6,87 ℓ; 6,88 ℓ o 6,89 ℓ. •  2 3 2 1 0,10 1 3 3 0,02 5 5 4,16 € Sí, puede comprarlo. 14  •  Lara: 2,9 min José: 2,009 min Olga: 2,09 min Ha llegado primero José. •  David: 7 m aprox. Lidia: 2 m aprox. •  Pantalón: 35,60 €. Camisa: 17,30 €. Abrigo: 80,20 €. 15  •  Cerrillo: 37,8 ºC. Valverde: 0,5 ºC. •  Villares, Valverde y Cobijo. •  Villares y Cerrillo. Demuestra tu talento 16   Escribimos las fracciones en forma de número decimal y, después, comparamos. 0,7        0,71        0,69        0,695 0,69 , 695 1.000 , 0,7 , 71 100 Notas Competencias •  Competencia matemática, científica y tecnológica. La situación presentada en la actividad 15 presenta un contexto en el que se relacionan las Matemáticas con conceptos del ámbito científico como son las temperaturas máximas y mínimas. Señale la relación existente entre las diferentes disciplinas de este ámbito y anímelos a buscar y utilizar, siempre que puedan, esas conexiones. Pídales que planteen a sus compañeros preguntas similares a las ofrecidas. 37
  • 38.
    Estudiar la evoluciónde un precio En la clase de 4.º están haciendo un trabajo sobre la variación en los precios de los combustibles. Han representado en un gráfico el precio medio en euros de un litro en algunos meses de 2014. SABER HACER 1 Observa el gráfico y resuelve. ¿Cuánto valía el litro de gasoil en marzo? ¿Y el de gasolina en mayo? ¿En qué mes aumentó el precio del gasoil con respecto al mes anterior? ¿En qué meses fue igual el precio de la gasolina? ¿En qué meses el litro de gasoil costaba más de 1,35 €? ¿En qué meses el litro de gasolina costaba menos de 1,41 €? 2 TRABAJO COOPERATIVO. Resuelve con tu compañero. Redondead cada precio del gráfico a los céntimos de euro y contestad de nuevo las preguntas de la actividad 1. ¿Hay alguna diferencia con las respuestas obtenidas anteriormente? 1,42 1,41 1,4 1,39 1,38 1,37 1,36 1,35 1,34 1,33 1,32 1,31 1,3 Enero JunioMayoAbrilMarzoFebrero Gasoil Gasolina 1,404 1,411 1,401 1,412 1,355 1,355 1,338 1,346 1,3381,338 1,402 1,402 110 ES0000000024590 663006-Unidad 07_22590.indd 110 10/03/2015 13:17:06 Inteligencia interpersonal Propósitos •  Desarrollar la competencia matemática resolviendo   una situación real. •  Repasar contenidos básicos. Actividades pág. 110 1   •  Gasoil en marzo: 1,338 €. Gasolina en mayo: 1,402 €. •  Aumentó en junio. •  En abril y mayo. •  En enero y febrero. •  En enero, marzo, abril y mayo. 2   Gasolina: 1,40 1,41 1,40  1,40 1,40 1,41  Gasoil: 1,36 1,36 1,34  1,34 1,34 1,35 •  Gasoil en marzo: 1,34 €. Gasolina en mayo: 1,40 €. •  Aumentó en junio. •  En enero, marzo, abril y mayo. •  En enero y febrero. •  En enero, marzo, abril y mayo. Actividades pág. 111 1   •  200.071 •  8.402.093 •  3 4 •  1 5 •  7 10 •  2 6 2   •  96.108 •  c 5 3.619, r 5 5 •  87.788 •  c 5 762, r 5 14 •  344.454 •  c 5 1.236, r 5 40 3   •  7 2 6 5 1 •  3 1 10 2 1 5 12 •  9 2 5 5 4 •  8 : 8 1 3 5 4 •  3 2 1 5 2 •  9 2 2 2 6 5 1 4   •  Siete novenos. •  Tres octavos. •  Nueve décimos. •  Cuatro quintos. 5   •  11 5 y 10 7 6   •  2 3 . 2 5 •  8 10 . 3 10 •  5 2 . 5 7   Desarrollo de la competencia matemática •  En esta página los alumnos tienen que aplicar distintos conceptos estudiados en la unidad para resolver una situación de la vida real. Hágales observar en el gráfico que el precio de los combustibles   varía de un mes a otro. A la hora de abordar el trabajo cooperativo,   pídales que intenten expresar los nuevos datos de forma gráfica. También puede ser interesante que busquen información actualizada sobre los precios de ambos combustibles en fechas próximas. 38
  • 39.
    4 Escribe cómose lee cada fracción. 7 9 3 8 9 10 4 5 5 Copia en tu cuaderno las fracciones que sean impropias. 11 5 7 10 10 7 6 9 6 Compara cada pareja de fracciones. 7 Calcula. 2 3 de 120 4 5 de 165 Seis octavos de 160. 1 Escribe con cifras. Doscientos mil setenta y uno Ocho millones cuatrocientos dos mil noventa y tres Tres cuartos Un quinto Siete décimos Dos sextos 2 Calcula. 86.234 1 9.874 28.957 : 8 91.663 2 3.875 31.256 : 41 921 3 374 68.020 : 55 3 Calcula. 7 2 2 3 3 3 1 2 3 5 2 1 9 2 (6 2 1) 8 : (2 1 6) 1 3 9 2 6 2 1 9 2 8 : 4 2 6 8 María ha cocinado 200 pasteles. Tres quintos son de chocolate y el resto de fresa. ¿De qué sabor ha cocinado más pasteles? 9 A una excursión se apuntaron 25 personas, que pagaban 20 € cada una. Se borraron 5 personas. ¿Cuánto tuvo que pagar cada una de las que quedaron si el precio total seguía siendo el mismo? 10 Sonia ha pintado tres séptimos de una figura y Laura ha pintado tres cuartos de una figura igual. ¿Cuál ha pintado más? 11 Se han envasado 15.000 bolígrafos en cajas de 6 unidades. Después, se hicieron paquetes de 8 cajas. ¿Cuántos paquetes se han obtenido? ¿Sobraron cajas? 12 En Valverde cosecharon 25.000 kg de patatas. Se quedaron 1.800 kg y el resto lo envasaron en sacos de 50 kg. ¿Cuántos sacos obtuvieron? 13 Un quinto de los 180 alumnos de Dibujo vienen a clase en bicicleta. La mitad de ellos son chicas. ¿Cuántas chicas vienen a clase en bicicleta? Problemas REPASO ACUMULATIVO 7 2 3 y 2 5 8 10 y 3 10 5 2 y 5 7 111 ES0000000024590 663006-Unidad 07_22590.indd 111 10/03/2015 13:17:06 UNIDAD 7 7 •  2 3 de 120 5 80 •  4 5 de 165 5 132 •  6 8 de 160 5 120 8 3 5 de 200 5 120 de chocolate 200 2 120 5 80 de fresa Ha cocinado más de chocolate. 9 20 3 5 5 100 100 : 20 5 5 20 1 5 5 25 Tuvo que pagar 25 €. 10  3 7 , 3 4 Ha pintado más Laura. 11 15.000 : 6 5 2.500 2.500 : 8 c 5 312, r 5 4 Se han obtenido 312 paquetes y han sobrado 4 cajas. 12 25.000 2 1.800 5 23.200 23.200 : 50 5 464 Obtuvieron 464 sacos. 13 1 5 de 180 5 36 36 : 2 5 18 Vienen en bicicleta 18 chicas. Notas Repaso en común • Reúna a los alumnos en pequeños grupos y pida a cada uno de ellos que proponga en una hoja distintas actividades relacionadas con los contenidos tratados en la unidad. Pueden ayudarse de las planteadas en el libro de texto. Un grupo trabajará las unidades decimales, otro los números decimales, otro la comparación y otro las aproximaciones. Después, reúna todas las hojas y entregue a cada alumno un cuaderno de repaso formado por todas ellas para que practique. Resuelva algunas de ellas, las que susciten mayores dificultades, en común. 39
  • 40.
    Operaciones con números decimales88 Contenidosde la unidad SABER NÚMEROS Y OPERACIONES • Suma de números decimales. •  Resta de números decimales. •  Multiplicación de números decimales. SABER HACER NÚMEROS Y OPERACIONES • Cálculo de sumas de números decimales y de fracciones decimales. • Cálculo de restas de números decimales y de fracciones decimales. • Cálculo de operaciones combinadas de sumas y restas de decimales. • Multiplicación de números decimales. • Multiplicación de un número decimal por un natural y por la unidad seguida de ceros. • Resolución de problemas utilizando la suma, resta y multiplicación de números decimales. RESOLUCIÓN DE PROBLEMAS • Escritura de un problema obteniendo los datos de su resolución. • Invención de un problema utilizando unas palabras y unos cálculos.   TAREA FINAL • Revisar una factura. FORMACIÓN EN VALORES • Valoración de las operaciones con decimales para la resolución de situaciones reales. • Interés por la resolución de problemas. 40
  • 41.
    BIBLIOTECA DEL PROFESORADO Programacióndidáctica de aula Recursos para la evaluación • Evaluación de contenidos. Unidad 8: pruebas de control B y A. • Evaluación por competencias. Prueba 8. •  Rúbrica. Unidad 8. Enseñanza individualizada • Plan de mejora. Unidad 8. • Programa de ampliación. Unidad 8. Proyectos de trabajo cooperativo • Proyecto del segundo trimestre. Recursos complementarios • Fichas para el desarrollo de la inteligencia. • Operaciones y problemas. Aprendizaje eficaz • Técnicas de estudio y presentación de exámenes. Proyectos interdisciplinares • Programa de Educación en valores. • Programa de Educación emocional. • Inteligencias múltiples. RECURSOS DIGITALES LibroMedia • Unidad 8: actividades y recursos. MATERIAL DE AULA Láminas OTROS MATERIALES DEL PROYECTO Cuaderno del alumno • Segundo trimestre. Unidad 8. Solución de problemas. Método DECA SUGERENCIA DE TEMPORALIZACIÓN Enero MarzoFebrero ES0000000024590 663006_Matematicas_4_GRAZ_24259 PRIMARIA PRIMARIA Matemáticas PRIMARIA ANDALUCÍAMatemáticas ANDALUCÍA Matemáticas ANDALUCÍA ES0000 000024 590 663006 _Matem aticas_4_GRA Z_2425 9.indd 1 04/03/2 015 11:21:19 ES0000000024593 663039_Cdno_Matematicas_4-2_22732 PRIMARIA Matemáticas Segundo trimestre Matemáticas Segundo trimestre PRIMARIA CUADERNO CUADERNO ES0000000024593 663039_Cdno_Matematicas_4-2_22732.indd 1 19/02/2015 16:56:18 41
  • 42.
    8 Operaciones con números decimales Laolimpíada de primavera Cada año en el colegio, cuando llega la primavera, celebran su propia olimpíada. Se realizan muchas pruebas y todos tienen la oportunidad de participar en ellas. Una de las más famosas es la vuelta al colegio. ¡Está tan disputada que tienen que medir los tiempos en décimas de segundo! Tiempos en la vuelTa al ColeGio mario 23,8 s Teresa 23,4 s andrés 24,6 s mercedes 24,2 s 112 ES0000000024590 663006-Unidad 08_22591.indd 112 10/03/2015 13:16:31 TiEMPOs En LA vUELTA AL COLEGiO Mario 23,8 s Teresa 23,4 s Andrés 24,6 s Mercedes 24,2 s Propósitos •  Reconocer situaciones reales en las que se utilicen números decimales. •  Recordar los conceptos básicos necesarios para el desarrollo de la unidad. Previsión de dificultades •  Algunos alumnos pueden tener dificultad en la colocación de los números decimales para calcular sumas y restas cuando los números tienen distinto número de cifras decimales. Ayúdeles explicando   que las comas de los números decimales deben estar en la misma columna y la coma del resultado estará siempre colocada debajo   de ellas. •  Vigile que los alumnos colocan correctamente la coma en   el resultado de los productos al multiplicar decimales. En ocasiones lo suelen olvidar o colocar mal. Pídales que razonen a menudo cuántas cifras deben separar   con la coma. Trabajo colectivo sobre la lámina Lea la situación planteada y pida   a los alumnos que lean en el cuadro   el tiempo que tardó cada niño en dar la vuelta al colegio. Pídales que recuerden cómo se leen esos números, qué partes tienen, cuál   es el valor de cada cifra… 1   Mario: 23,8 s. Parte entera: 23. Parte decimal: 8. 2   Menos de 24 s: Mario y Teresa. Más de 23,9 s: Andrés   y Mercedes. 3   Recuerde a los alumnos, si es necesario, cómo se comparan números decimales.  23,4 , 23,8 , 24,2 , 24,6 4   R. M.      24,3      24,4      24,5  Si lo cree conveniente puede explicar a los alumnos que entre dos números decimales hay infinitos números decimales. Otras formas de empezar •  Pida a los alumnos que expresen oralmente situaciones reales   en las que se utilizan números decimales y que pongan algunos ejemplos. Pregunte por qué creen que son necesarios en esas situaciones los números decimales y que expliquen los inconvenientes que habría si no se pudieran utilizar. Aporte algunos ejemplos de contextos en los que sea necesario sumarlos, restarlos o multiplicarlos y pida a los alumnos que aporten otros ellos mismos. 42
  • 43.
    1 ¿Qué númeroexpresa el tiempo que tardó Mario? ¿Cuál es su parte entera? ¿Y su parte decimal? 2 ¿Quiénes tardaron menos de 24 segundos en la vuelta al colegio? ¿Y más de 23,9 segundos? 3 Ordena los cuatro tiempos de menor a mayor. 4 EXPRESIÓN ORAL. Di dos tiempos que sean mayores que el de Mercedes pero menores que el de Andrés. Explica cómo los has obtenido. Lee, comprende y razona Números decimales: lectura y descomposición Los números decimales tienen una parte entera, a la izquierda de la coma, y una parte decimal, a la derecha de la coma. Parte entera: 13. Parte decimal: 75. Lectura: 13 unidades y 75 centésimas o 13 coma 75. Descomposición: 1 decena 1 3 unidades 1 7 décimas 1 5 centésimas 1 D 1 3 U 1 7 d 1 5 c 10 1 3 1 0,7 1 0,05 1 Escribe cómo se lee cada número y su descomposición. 3,9 18,36 27,04 6,198 2,031 11,005 Comparación de números decimales Para comparar números decimales, primero compara sus partes enteras; si son iguales, compara las décimas; si también lo son, las centésimas, y así sucesivamente. 2 Compara cada pareja de números. 6,75 y 7 8,36 y 8,39 7,042 y 7,03 5,003 y 5,011 ¿Qué sabes ya? TAREA FINAL Revisar una factura Al final de la unidad revisarás si una factura es correcta. Antes, aprenderás a sumar, restar y multiplicar números decimales. SABER HACER 3,82 , 4 7,16 . 7,12 9,325 , 9,328 13,75 113 ES0000000024590 663006-Unidad 08_22591.indd 113 10/03/2015 13:16:33 UNIDAD 8 ¿Qué sabes ya? Asegúrese de que los alumnos dominan los procedimientos de lectura, escritura, descomposición y comparación de decimales ya que son muy importantes para que aborden con éxito la unidad. 1   •  3 unidades y 9 décimas 3 1 0,9 •  18 unidades y 36 centésimas 10 1 8 1 0,3 1 0,06 •  27 unidades y 4 centésimas 20 1 7 1 0,04 •  6 unidades y 198 milésimas 6 1 0,1 1 0,09 1 0,008 •  2 unidades y 31 milésimas 2 1 0,03 1 0,001 •  11 unidades y 5 milésimas 10 1 1 1 0,005 2   •  6,75 , 7 •  8,36 , 8,39 •  7,042 . 7,03 •  5,003 , 5,011 Notas Competencias •  Comunicación lingüística. Al realizar las actividades propuestas después de la lectura es importante que los alumnos utilicen correctamente el lenguaje matemático para expresarse. Anímelos a ser correctos y compruebe que lo hacen de forma clara. •  Aprender a aprender. Señale que el aprendizaje es un proceso continuo y que después de estudiar los números decimales en la unidad anterior van a seguir aprendiendo sobre ellos; ahora van a aprender a sumarlos, restarlos y multiplicarlos. Inteligencia lingüística 43
  • 44.
    Suma de númerosdecimales 1 Copia en tu cuaderno y calcula. 2 Coloca los números y calcula. 7,8 1 2,9 27,6 1 3,905 14,29 1 21,84 12,667 1 4,82 6,075 1 8,399 9,66 1 96,553 3 Piensa y contesta. Si sumas dos números con dos cifras decimales que sean menores que 10, ¿cuál es el valor máximo que puede tener esa suma? Michi pesa 15,78 kg y su cría, Sol, pesa 9,6 kg. ¿Cuántos kilos pesan los dos juntos? Suma 15,78 y 9,6 1.º Coloca un número debajo del otro, de forma que coincidan en la misma columna las cifras del mismo orden. D U d c 1 5, 7 8 1 9, 6 2.º Suma como si fueran números naturales y escribe una coma en el resultado, debajo de la columna de las comas. D U d c 1 5, 7 8 1 9, 6 2 5, 3 8 Los dos juntos pesan 25,38 kg. Para sumar números decimales, se colocan de forma que coincidan en la misma columna las cifras del mismo orden. Después, se suman como si fueran números naturales y se coloca una coma en el resultado debajo de la columna de las comas. D U d c 1 5, 7 8 1 3 2, 0 7 D U d c m 7 6, 9 1 8 4, 6 5 2 C D U d c 4 2 9, 6 1 7 8, 7 4 PRESTA ATENCIÓN Fíjate en que las comas de ambos números estén en la misma columna. Pon la coma en el resultado. 9,6 15,78 114 ES0000000024590 663006-Unidad 08_22591.indd 114 10/03/2015 13:16:35 Propósitos •  Sumar dos o más números decimales. •  Resolver problemas de sumas   de números decimales. Sugerencias didácticas Para explicar. Lea la situación planteada y pregunte a los alumnos qué operación hay que realizar para resolverla. Escriba la suma correspondiente en la pizarra   y resuélvala explicando los pasos que hay que seguir. Haga especial hincapié en la colocación de los números decimales. Señale que en las sumas la coma del resultado quedará colocada bajo las comas de los sumandos. Para reforzar. Pregunte a los alumnos cómo sumarían un número natural y un decimal. Hágales ver que podemos considerar a los números naturales como números decimales sin parte decimal. Actividades 1   •  47,85 •  161,552 •  508,34 2   •  10,7 •  31,505 •  36,13 •  17,487 •  14,474 •  106,213 3   Pregúnteles cuál es el mayor número decimal con 2 cifras decimales menor que 10. Deles un tiempo para pensar y hágales ver que ese número es 9,99 y, por tanto, el máximo valor de la suma será 19,98. 4   •  (2,6 1 3,5) 1 4,8 5 10,9  2,6 1 (3,5 1 4,8) 5 10,9 •  (8,25 1 1,9) 1 6,74 5 16,89 8,25 1 (1,9 1 6,74) 5 16,89 •  (0,372 1 1,6) 1 2,88 5 4,852 0,372 1 (1,6 1 2,88) 5 4,852 5   •  0,8 1 0,36 5 1,16 •  0,178 1 0,9 5 1,078 •  0,71 1 0,071 5 0,781 •  0,6 1 0,806 5 1,406 Otras actividades •  Forme grupos de tres alumnos y haga que cada grupo prepare cinco tarjetas con estos números decimales. Pida a cada grupo que ponga las tarjetas boca abajo y cada alumno,   por turno, cogerá dos tarjetas y calculará la suma correspondiente, volviendo a dejar las dos tarjetas en el montón. Después, haga que comparen los resultados obtenidos y ganará el alumno que haya obtenido la suma mayor. 2,75 0,469 8,53 9,732 46,8 44
  • 45.
    8 4 Suma cadagrupo de tres números de dos formas cambiando el orden de los sumandos. ¿Obtienes el mismo resultado? ¿Por qué crees que ocurre? 5 Suma estas fracciones. Exprésalas primero en forma de número decimal. 8 10 1 36 100 178 1.000 1 9 10 71 100 1 71 1.000 6 10 1 806 1.000 Problemas 6 Resuelve. Un gato pesa 5,2 kg, una tortuga 1,78 kg y un loro 0,625 kg. – ¿Cuánto pesan juntos el gato y la tortuga? ¿Y la tortuga y el loro? – ¿Cuánto pesan los tres animales juntos? Un caracol trepó tres días por una pared. El primer día trepó 2,78 m, el segundo día 4,5 m y el tercero 5,81 m. ¿Qué distancia trepó en total? Lidia sacó en dos exámenes 8,5 puntos y 6,78 puntos, respectivamente. Nadia sacó 8,71 puntos y 6,59 puntos en los mismos exámenes. ¿Quién sacó más puntuación total? Miguel pesa 42,75 kg y su hermana Eva pesa 1,8 kg más que él. ¿Cuántos kilos pesan los dos juntos? Suma 11 a un número: primero suma 10 y luego suma 1 37 1 11 213 1 11 1.872 1 11 45 1 11 562 1 11 3.624 1 11 58 1 11 718 1 11 6.513 1 11 69 1 11 849 1 11 9.129 1 11 CÁLCULO MENTAL 2,6 1 3,5 1 4,8 0,372 1 1,6 1 2,88 8,25 1 1,9 1 6,74 EJEMPLO 8 10 1 36 100 5 0,8 1 … 5 … 347 357 358 1 10 1 1 1 11 115 ES0000000024590 663006-Unidad 08_22591.indd 115 10/03/2015 13:16:36 UNIDAD 8 6   •  El gato y la tortuga: 5,2 kg 1 1,78 kg 5 6,98 kg La tortuga y el loro: 1,78 kg 1 0,625 kg 5 2,405 kg Los tres juntos: 5,2 kg 1 1,78 kg 1 0,625 kg 5 5 7,605 kg •  2,78 1 4,5 1 5,81 5 13,09 En total trepó 13,09 metros. •  Lidia: 8,5 1 6,78 5 15,28 Sacó 15,28 puntos. Nadia: 8,71 1 6,59 5 15,30 Sacó 15,30 puntos. Sacó más puntuación Nadia. •  42,75 1 1,8 5 44,55 42,75 1 44,55 5 87,30 Los dos juntos pesan 87,30 kg. Cálculo mental •  48 •  224 •  1.883 •  56 •  573 •  3.635 •  69 •  729 •  6.524 •  80 •  860 •  9.140 Notas Otras actividades •  Pida a cada alumno que complete una ficha con su nombre, su altura en metros y su peso en kilos. A continuación, haga grupos de tres alumnos y pídales que calculen actividades similares a las siguientes: –  La altura total de los dos más altos. –  El peso total de los dos de menor peso. –  La altura total de los tres. –  El peso total de los tres. 45
  • 46.
    Resta de númerosdecimales 1 Coloca los números y calcula. 9,6 2 1,9 27,16 2 3,9 23,5 2 3,76 18,91 2 4,675 4,8 2 1,999 8,4 2 2,067 2 Calcula el término que falta en cada caso. ★ 1 2,5 5 3 ★ 2 1,28 5 4 ★ 1 1,3 5 2,6 ★ 2 3,6 5 5,889 6,72 1 ★ 5 9,126 11,2 2 ★ 5 8,88 1,8 1 ★ 5 4,675 9,75 2 ★ 5 2,6 En la prueba de salto de longitud, Mario ha saltado 4,75 m y Olga ha saltado 5,2 m. ¿Cuánto ha saltado Olga más que Mario? Resta 5,2 2 4,75 1.º Coloca un número debajo del otro, de forma que las comas concidan. Añade ceros si faltan cifras decimales. U d c 5, 2 0 2 4, 7 5 2.º Resta como si fueran números naturales y escribe una coma en el resultado debajo de la columna de las comas. U d c 5, 2 0 2 4, 7 5 0, 4 5 Olga ha saltado 0,45 m más que Mario. Para restar números decimales, se colocan de forma que coincidan en la misma columna las cifras del mismo orden. Se añaden ceros si faltan cifras decimales y, después, se resta como si fueran números naturales. Luego se coloca la coma en el resultado. PRESTA ATENCIÓN Coloca ceros en los lugares en los que falten cifras decimales. EJEMPLO ★ 5 3 2 2,5 5 0,5 EJEMPLO ★ 5 4 1 1,28 5 5,28 116 ES0000000024590 663006-Unidad 08_22591.indd 116 10/03/2015 13:16:37 Propósitos •  Restar números decimales. •  Resolver situaciones de resta. Sugerencias didácticas Para explicar. Pida a un alumno   que lea la situación propuesta   y pregúnteles qué operación hay que realizar para resolverla. Escriba   la resta correspondiente en la pizarra explicando que, cuando los números decimales tienen distinto número   de cifras decimales, completamos   con ceros. Muestre la similitud con   la suma al colocar los términos. Para reforzar. Escriba en la pizarra varias restas de números decimales con distinto número de cifras decimales, y pídales que coloquen   los números para restarlos y completen con los ceros necesarios. Después, calcularán esas restas. Pregúnteles cómo realizarían la resta de un número decimal y un natural,   y trabaje algún ejemplo en común. Actividades 1   •  7,7 •  23,26 •  19,74 •  14,235 •  2,801 •  6,333 2   •  5 3 2 2,5 5 0,5 •  5 2,6 2 1,3 5 1,3 •  5 9,126 2 6,72 5 2,406 •  5 4,675 2 1,8 5 2,875 •  5 4 1 1,28 5 5,28 •  5 5,889 1 3,6 5 9,489 •  5 11,2 2 8,88 5 2,32 •  5 9,75 2 2,6 5 7,15 3   •  6,1 2 1,89 5 4,21 •  5,42 1 6,7 5 12,12 •  7,2 2 0,667 5 6,533 •  5 1 0,61 5 5,61 •  8,21 2 0,11 5 8,10 •  9,6 2 1,733 5 7,867 4   •  0,5 2 0,12 5 0,38 •  0,45 2 0,009 5 0,441 •  0,7 2 0,002 5 0,698 •  0,06 2 0,004 5 0,056 Otras actividades • Pida que cada alumno escriba en su cuaderno tres números decimales   con una, dos y tres cifras decimales respectivamente, y calcule todas   las restas posibles con los números que ha escrito. Haga que un alumno salga a la pizarra y escriba los números que   ha escrito y las restas correspondientes. Entre todos se comprobará   si la solución dada es o no correcta. Puede repetir el proceso con varios alumnos. 46
  • 47.
    8 RAZONAMIENTO Problemas 5 Resuelve. Manuel hacomprado 7,5 kg de manzanas, 4,92 kg de peras y 1,925 kg de plátanos. ¿Cuánto pesan las manzanas más que las peras? ¿Y los plátanos menos que las manzanas? Ruth corrió tres veces los 100 m lisos. La primera vez tardó 15,2 s, la segunda vez 0,4 s menos que la primera y la tercera vez 0,38 s menos que la segunda. ¿Cuánto tardó la tercera vez? Andrés pesa 57,50 kg y su prima Ana pesa 9,8 kg menos que él. ¿Cuántos kilos pesan los dos juntos? Lola tenía 40 €. Gastó 8,93 € en un pañuelo y 12,79 € en unos pendientes. ¿Cuánto dinero le quedó? 3 Halla el resultado de estas expresiones. Sigue el mismo orden que en las operaciones combinadas con números naturales. 2,5 1 3,6 2 1,89 5 1 (2,6 2 1,99) 8,42 2 3 1 6,7 8,21 2 (5 2 4,89) 9,6 2 2,4 2 0,667 9,6 2 (2,4 2 0,667) 4 Resta estas fracciones. Exprésalas primero en forma de número decimal. 5 10 2 12 100 45 100 2 9 1.000 7 10 2 2 1.000 6 100 2 4 1.000 RECUERDA 1.º Operaciones de los paréntesis. 2.º Sumas y restas en el orden en el que aparecen. 117 Piensa y contesta. Pon ejemplos si es necesario. La suma de dos números decimales ¿puede ser un número natural? ¿Y la resta de dos números decimales? Si restas dos números decimales con dos cifras en su parte decimal, ¿puedes obtener otro con una sola cifra decimal? 2,3 1,49 8,278 ES0000000024590 663006-Unidad 08_22591.indd 117 10/03/2015 13:16:38 UNIDAD 8 5   •  7,5 2 4,92 5 2,58 Las manzanas pesan 2,58 kg más que las peras. 7,5 2 1,925 5 5,575 Los plátanos pesan 5,575 kg menos que las manzanas. •  15,2 2 0,4 5 14,8 14,8 2 0,38 5 14,42 La tercera vez tardó 14,42 s. •  57,50 2 9,8 5 47,70 57,50 1 47,70 5 105,20 Los dos juntos pesan 105,20 kg. •  8,93 1 12,79 5 21,72 40 2 21,72 5 18,28 Le quedaron 18,28 €. Razonamiento •  Sí, la suma y la resta de dos números decimales puede ser un número natural. Basta con que sean iguales o bien que sumen una unidad. Ejemplos: 12,65 1 3,35 516 34,56 2 9,56 5 25 •  Sí, basta con que sus cifras de las centésimas sean iguales. Ejemplo: 14,25 2 6,75 5 7,50 Notas Otras actividades •  Prepare un dado pegando en sus caras pegatinas, de forma que haya dos caras con un 1, otras dos con un 2 y otras dos con un 3. Lance el dado y pida a un alumno que diga un número decimal cuyo número de cifras decimales sea el que haya salido en el dado. Escríbalo en la pizarra. Repita el proceso para obtener otro número y pida a los alumnos que sumen y resten los dos números escritos. •  Puede pedir a los alumnos que investiguen si la suma de decimales cumple las propiedades conmutativa y asociativa. Con la resta, puede pedirles que hagan la prueba de las restas que realicen. 47
  • 48.
    Multiplicación de númerosdecimales 1 Calcula en tu cuaderno. No olvides colocar la coma en su lugar correcto. 3,5 3 1,6 0,36 3 9,2 3,012 3 5,4 25,167 3 3,8 2,18 3 4,7 1,7 3 37,88 2,3 3 0,194 4,7 3 1,006 2 Escribe con cifras y calcula. Seis unidades y nueve centésimas por tres unidades y doce milésimas. Cuarenta y ocho coma dos por diecisiete coma treinta y seis. 3 Calcula estos productos de un número decimal por un número natural. 3,7 3 9 9,25 3 7 6,174 3 6 8,75 3 12 6,789 3 34 Teresa ha comprado 4,6 kg de naranjas para hacer zumo. Cada kilo cuesta 1,25 €. ¿Cuánto han costado en total? Multiplica 1,25 por 4,6 1.º Multiplica los números como si fueran números naturales. 2.º En el resultado, separa con una coma, a partir de la derecha, tantas cifras decimales como tengan en total los dos factores. Las naranjas han costado 5,75 €. Para multiplicar dos números decimales, se multiplican como si fueran números naturales, y en el resultado se separan, con una coma, a partir de la derecha, tantas cifras decimales como tengan en total los dos factores. 1, 2 5 3 4, 6 7 5 0 5 0 0 5 7 5 0 HAZLO ASÍ 1, 2 5 3 4, 6 7 5 0 5 0 0 5, 7 5 0 2 cifras decimales 1 cifra decimal 2 1 1 5 3 3 cifras decimales Considera el número natural como un número decimal sin cifras decimales. 3 3 5,61 5 16,83 2 cifras decimales 118 ES0000000024590 663006-Unidad 08_22591.indd 118 10/03/2015 13:16:39 Propósitos •  Multiplicar números decimales. •  Resolver situaciones   de multiplicación. Sugerencias didácticas Para explicar. Haga que un alumno lea la situación planteada y pregúnteles la operación que debemos calcular para resolverla. Resuelva la multiplicación correspondiente en la pizarra, explicando el procedimiento que hay que seguir. Haga especial hincapié   en la colocación de la coma en el resultado. Deje claro que en este caso la coma del resultado no se coloca bajo la coma de los términos, como   sí que ocurría en la suma y la resta. Pregúnteles a menudo dónde va la coma colocada para que interioricen este procedimiento. Comente los casos particulares de   los productos por números naturales   y por la unidad seguida de ceros. Para reforzar. Puede escribir en   la pizarra varias multiplicaciones   de números decimales y preguntar   a los alumnos cuántas cifras decimales tendrá cada resultado. Actividades 1   •  5,6 •  16,2648 •  10,246 •  0,4462 •  3,312 •  95,6346 •  64,396 •  4,7282 2   •  6,09 3 3,012 5 18,34308 •  48,2 3 17,36 5 836,752 3   •  33,3 •  64,75 •  37,044 •  105 •  230,826 4   •  30,7 •  137 •  28 •  13,4 •  276,15 •  2.800 •  620 •  4.670 5   •  0,012 3 100 5 1,2 m  La fila mide 1,2 m. Otras actividades •  Pida a los alumnos que confeccionen tablas similares a la siguiente,   y que se las intercambien entre ellos para resolverlas. Cada uno deberá después comprobar la corrección de los resultados   de su compañero. 3 3 3 5 3 7 3 10 3 100 3 1.000 2,38 7,3 7,982 0,097 3,42 48
  • 49.
    8 4 Multiplica cadanúmero decimal por la unidad seguida de ceros. 3,07 3 10 2,8 3 10 27,615 3 10 6,2 3 100 1,37 3 100 0,134 3 100 2,8 3 1.000 4,67 3 1.000 Problemas 5 Resuelve. Cien hormigas se han colocado en fila. Cada una de ellas mide 0,012 m. ¿Cuántos metros mide en total la fila de hormigas? Marta compró una piña por 2,75 € y 1,4 kg de fresas que costaban 2,80 € el kilo. ¿Cuánto pagó Marta por su compra? Un tren lleva 10 vagones, que miden 7,8 m cada uno, y una locomotora, que mide 2,6 m más que un vagón. ¿Cuál es la longitud total del tren? En una tienda tienen 100 paquetes de zumo de 0,25 ℓ cada uno y 32 botellas de 1,5 ℓ. ¿Cuántos litros de zumo tienen en total en la tienda? HAZLO ASÍ Para multiplicar un número decimal por la unidad seguida de ceros se desplaza la coma a la derecha tantos lugares como ceros siguen a la unidad. Si es necesario, se añaden ceros. 12,45 3 10 5 124,5 9,8 3 100 5 980 1 cero 1 lugar 2 ceros 2 lugares a la derecha a la derecha Suma 9 a un número: primero suma 10 y luego resta 1 CÁLCULO MENTAL 27 1 9 213 1 9 1.345 1 9 48 1 9 342 1 9 2.068 1 9 56 1 9 781 1 9 7.612 1 9 75 1 9 864 1 9 9.601 1 9 347 357 356 1 10 2 1 1 9 119 ES0000000024590 663006-Unidad 08_22591.indd 119 10/03/2015 13:16:40 UNIDAD 8 • 1,4 3 2,80 5 3,92 2,75 1 3,92 5 6,67 Marta pagó 6,67 €. • 7,8 1 2,6 5 10,4 m 7,8 3 10 5 78 m 10,4 1 78 5 88,4 m La longitud del tren es 88,4 m. • 0,25 3 100 5 25 32 3 1,5 5 48 48 1 25 5 73 Tienen un total de 73 litros. Cálculo mental •  36 •  222 •  1.354 •  57 •  351 •  2.077 •  65 •  790 •  7.621 •  84 •  873 •  9.610 Notas Otras actividades •  Pida a los alumnos que inventen problemas que se resuelvan con una multiplicación de un decimal por un natural o multiplicando dos decimales. Después, los intercambiarán con sus compañeros y cada uno resolverá el problema creado por el otro. Más tarde, cada alumno comprobará si su problema fue bien resuelto. Póngales algunos ejemplos para ayudarlos si lo estima oportuno: – La ruta de un conductor de autobús es de 12,75 km. ¿Cuántos kilómetros recorre diariamente si cada día hace la misma ruta 9 veces? ¿Cuántos kilómetros recorrerá a la semana? Inteligencia naturalista 49
  • 50.
    Escribe en tucuaderno cada problema y completa los datos que faltan teniendo en cuenta su resolución. 1 Nieves compró un libro por €. También compró un disco, algo más caro, por €. Pagó con €. ¿Cuánto dinero le quedó? 2 Miguel envasó avellanas en bolsas de kg. Envasó kg y vendió bolsas. ¿Cuántas bolsas no pudo vender? 3 Luna vendió varias sandías a € cada una. Había recogido , pero de ellas estaban estropeadas. ¿Cuánto dinero obtuvo? Vamos a leer el problema y su resolución. Después, completaremos los datos que faltan en el enunciado a partir de esa resolución. Ramón compró un abrigo por €. Tenía varios billetes de € y pagó con de ellos. ¿Cuánto dinero le devolvieron? Al leer el problema sabemos que pagó una cantidad mayor que el precio del abrigo. Además, los billetes tienen que ser de 20 €, viendo los números que aparecen en los cálculos. Ramón compró un abrigo por 75 €. Tenía varios billetes de 20 € y pagó con 4 de ellos. ¿Cuánto dinero le devolvieron? Extraer datos de la resolución de un problema Solución de problemas Resolución 50 2 12 5 38 38 2 10 5 28 Resolución 50 2 8 5 42 42 3 4 5 168 Resolución 240 : 5 5 48 48 2 19 5 29 Resolución 4 3 20 5 80 80 2 75 5 5 120 ES0000000024590 663006-Unidad 08_22591.indd 120 10/03/2015 13:16:42 Propósitos •  Completar problemas extrayendo los datos de la resolución. •  Inventar problemas utilizando determinadas palabras y que se resuelvan con unos cálculos dados. Sugerencias didácticas Para explicar. Comente a los alumnos que en el enunciado   del problema faltan algunos datos   y señale que debemos completarlos obteniéndolos a partir de los cálculos de su resolución. Indíqueles que los primeros huecos   en el enunciado no corresponden necesariamente a los primeros datos de los cálculos. Deje que los alumnos vayan aportando sus propuestas, analizando la corrección de cada   una de ellas. Muestre la necesidad   de determinar si el enunciado obtenido tiene sentido y si se resuelve con los cálculos dados. Actividades 1   Nieves compró un libro por   10 €. También compró un disco algo más caro, por 12 €.   Pagó con 50 €. ¿Cuánto dinero   le quedó? 2   Miguel envasó avellanas en bolsas de 5 kg. Envasó 240 kg y vendió 19 bolsas. ¿Cuántas bolsas   no pudo vender? 3   Luna vendió varias sandías a 4 € cada una. Había recogido 50, pero 8 de ellas estaban estropeadas. ¿Cuánto dinero obtuvo? 4   Leonor compró una lavadora   que costaba 455 €. Pagó con   9 billetes de 50 € y un billete   de 5 €. ¿Cuánto dinero   le devolvieron? 5   A una excursión se apuntaron   130 hombres, pero se borraron 45 (o 20). Se apuntaron más mujeres que hombres, 150 mujeres,   y se borraron 20 (o 45). ¿Cuántas personas fueron al final? Otras actividades •  Agrupe a los alumnos y pida a cada grupo que escriba un problema   y lo resuelva. Después, en una hoja aparte, escribirán el enunciado   quitando los datos y, debajo de él, los cálculos que han usado   para resolverlo. Lo pasarán a otro grupo que intentará reconstruirlo.   Una vez hecho, cada grupo comprobará el desempeño de sus compañeros. Comente algunas de las propuestas y sus resoluciones en común. 50
  • 51.
    Fíjate en cadagrupo de palabras y cálculos, y escribe en tu cuaderno un problema en el que los utilices. adultos niños precio entrada 87 3 4 5 348 95 3 9 5 855 348 1 855 5 1.203 dinero compró repartió sobrinos 600 2 40 5 560 560 : 7 5 80 8 Fíjate en cada resolución y escribe el enunciado completo en tu cuaderno. 4 Leonor compró una lavadora que costaba €. Pagó con billetes de €, y un billete de €. ¿Cuánto dinero le devolvieron? 5 A una excursión se apuntaron hombres, pero se borraron . Se apuntaron más mujeres que hombres, mujeres, y se borraron . ¿Cuántas personas fueron al final? INVENTA TUS PROBLEMAS Fíjate en cada grupo de palabras y cálculos, y escribe en tu cuaderno un problema en el que los utilices. Resolución 600 : 2 5 300 300 : 5 5 60 60 3 4 5 240 6 Paula repartió en partes iguales las patatas que tenía. Envasó una parte en bolsas de kg y vendió cada bolsa a €. Si tenía kg de patatas, ¿cuánto dinero obtuvo? Resolución 9 3 50 5 450 450 1 5 5 455 455 2 453 5 2 Resolución 130 1 150 5 280 45 1 20 5 65 280 2 65 5 215 vendió 275 2 18 5 257 257 3 3 5 771 manzanas estropeadas 121 ES0000000024590 663006-Unidad 08_22591.indd 121 10/03/2015 13:16:44 UNIDAD 8 6 Paula repartió en 2 partes iguales las patatas que tenía. Envasó una parte en bolsas de 5 kg cada una y vendió cada bolsa a 4 €. ¿Cuánto dinero obtuvo? Inventa tus problemas •  R. M. Ricardo recogió 275 kg de manzanas. Tiró 18 kg que estaban estropeadas y vendió cada kilo a 3 €. ¿Cuánto dinero obtuvo Ricardo por la venta? •  R. M. Julia cobró un cheque de 600 €. Compró un sillón por 40 € y el resto lo repartió en partes iguales entre sus 7 sobrinos. ¿Cuánto dinero dio a cada uno? •  R. M. A una película de estreno asistieron 87 niños y 95 adultos. Cada entrada de niño costaba 4 € y la de adulto 9 €. ¿Cuánto se recaudó en total? Notas Competencias •  Iniciativa y emprendimiento. Las actividades de invención de problemas son un contexto muy adecuado para desarrollar esta competencia. Pida a los alumnos que lean detenidamente las palabras y los cálculos de la primera situación y expongan oralmente sus propuestas. Entre todos se comprobará si son o no correctas. Más tarde, déjeles que trabajen por sí mismos el resto de actividades y comente las diferentes aportaciones. Inteligencia interpersonal 51
  • 52.
    14,16 8,75 11,3 13,45 112,9 29,05 27,165 3 100 3 4 7Multiplica estos decimales. 2,8 3 3,9 9,21 3 3,87 4,28 3 5,36 3,6 3 2,84 2,725 3 1,4 4,2 3 4,35 8 Multiplica. 9 3 8,3 0,039 3 17 17,82 3 5 28 3 12,35 4 3 3,776 9,78 3 312 9 Multiplica cada uno de estos números por 10, por 100 y por 1.000. 10 Recuerda cómo se multiplica por la unidad seguida de ceros y halla el número que falta. 3 10 5 45 3 1.000 5 34 3 100 5 126,3 3 100 5 78 3 1.000 5 17 3 10 5 3,6 11 Calcula y completa en tu cuaderno. 12 Calcula y compara en tu cuaderno. 2,8 1 3,9 7 2 0,25 4,7 2 1,884 14,8 3 0,2 0,36 3 100 8,25 3 3,4 1 Suma estos números decimales. 3,9 1 2,75 0,86 1 2,99 1,667 1 2,4 6,57 1 8,075 9,28 1 0,997 15,4 1 16,803 2 Resta. 3,9 2 2,75 425,7 2 87,92 9,45 2 2,4 816,2 2 9,753 9,28 2 0,997 902,43 2 85,192 3 Piensa y contesta. María va a hacer todas las sumas y restas posibles con dos de estos tres números. Sin calcular, ¿qué suma dará un resultado mayor? ¿Qué resta dará un resultado menor? Calcula y comprueba tus respuestas. 4 Calcula el término que falta. Piensa si tienes que sumar o restar. 2 3,6 5 2,98 5,765 2 5 4,9 2 6,82 5 10,1 2,4 2 5 0,367 5 Calcula. 4,2 1 3,75 2 2,6 (4,6 2 2,94) 2 1 8,76 2 (2,4 2 1,77) 8,701 1 2,6 1 3 9,34 2 (8,6 1 0,13) 10 2 1,8 2 2,97 6 VOCABULARIO. Explica cómo se multiplican dos números decimales. ACTIVIDADES 6,75 9,127 4,8 8,4 3,16 0,025 15,7 26,04 9,102 122 ES0000000024590 663006-Unidad 08_22591.indd 122 10/03/2015 13:16:45 Propósitos •  Repasar los contenidos básicos   de la unidad. Actividades 1 •  6,65 •  3,85 •  4,067 •  14,645 •  10,277 •  32,203 2   •  1,15 •  337,78 •  7,05 •  806,447 •  8,283 •  817,238 3 Suma con el resultado mayor: 9,127 1 6,75 5 15,877  Resta con el resultado menor: 6,75 2 4,8 5 1,95 4 •  5 2,98 1 3,6 5 6,58 •  5 5,765 2 4,9 5 0,865 •  5 10,1 1 6,82 5 16,92 •  5 2,4 2 0,367 5 2,033 5 •  7,95 2 2,6 5 5,35 •  8,76 2 0,63 5 8,13 •  9,34 2 8,73 5 0,61 •  1,66 2 1 5 0,66 •  11,301 1 3 5 14,301 •  8,2 2 2,97 5 5,23 6 R. L. 7 •  10,92 •  35,6427 •  22,9408 •  10,224 •  3,815 •  18,27 8 •  74,7 •  0,663 •  89,1 •  345,8 •  15,104 •  3.051,36 9 •  8,4 F 84 F 840 F 8.400 •  3,16 F 31,6 F 316 F 3.160 •  0,025 F 0,25 F 2,5 F 25 •  15,7 F157 F 1.570 F15.700 •  26,04 F 260,4 F 2.604 F  F 26.040 •  9,102 F 91,02 F 910,2 F  F 9.102 10 •  5 4,5 •  5 0,034 •  5 1,263 •  5 0,78 •  5 0,017 •  5 0,36 11  •  14,16 2 17,61 2 10,445 •  11,3 2 2,25 2 9 •  8,75 2 21,65 2 2,165 Otras actividades • Plantee a los alumnos actividades para afianzar los contenidos estudiados   en la unidad. Puede proponer actividades de suma, resta y multiplicación   de números decimales como las que se indican a continuación. Suma 1,25 cada vez Resta 3,7 cada vez Multiplica por 0,2 cada vez 24,3 125 0,089 52
  • 53.
    15 Resuelve. Jaime esrepostero y tiene una receta secreta que usa para hacer la tarta de chocolate. ¿Cuántos kilos pesan en total la harina y el azúcar de una tarta? Si Jaime decide hacer 3 tartas, ¿cuántos kilos de mantequilla necesita? ¿Y de cacao? Para un encargo de 10 tartas, ¿cuántos kilos de azúcar necesita? ¿Y de harina? El mes pasado Jaime hizo 100 tartas de chocolate. ¿Gastó en ellas más o menos de 25 kg de mantequilla? ¿Cuántos kilos de cacao gastó? En un pedido de 8 tartas, ¿cuántos kilos más pesan la harina y la mantequilla que el azúcar y el cacao? Problemas 13 Resuelve. Jimena vende el metro de cordón a 3,40 €. Tenía un rollo de 10 m, vendió 1,85 m a un cliente y a otro cliente, el resto del rollo. ¿Cuánto pagó el segundo cliente? 14 Piensa y resuelve. Un modelo de coche gasta 7,26 ℓ de gasolina cada 100 km. ¿Cuánto gastará si recorre 500 km? ¿Y 1.000 km? Manuela medía 1,20 m. Creció 0,65 m y después 0,09 m. ¿Cuántos metros mide ahora Manuela? Carmen recogió 50 kg de peras. Guardó 7 kg para ella y vendió el resto a 3,75 € el kilo. ¿Cuánto dinero obtuvo? 15 Resuelve. Jaime es repostero y tiene una receta secreta que usa para hacer la tarta de chocolate. ¿Cuántos kilos pesan en total la harina y el azúcar de una tarta? Si Jaime decide hacer 3 tartas, ¿cuántos kilos de mantequilla necesita? ¿Y de cacao? Para un encargo de 10 tartas, ¿cuántos kilos de azúcar necesita? ¿Y de harina? El mes pasado Jaime hizo 100 tartas de chocolate. ¿Gastó en ellas más o menos de 25 kg de mantequilla? ¿Cuántos kilos de cacao gastó? En un pedido de 8 tartas, ¿cuántos kilos más pesan la harina y la mantequilla que el azúcar y el cacao? 8 16 ¿Cómo multiplicarías estas fracciones? Recuerda la relación entre decimales y fracciones. 7 10 3 2 10 3 100 3 5 10 9 10 3 6 100 Demuestra tu talento TARTA DE CHOCOLATE 0,2 kg de harina 0,25 kg de azúcar 0,24 kg de mantequilla 0,05 kg de cacao en polvo 1 sobre de levadura 6 huevos y canela 123 ES0000000024590 663006-Unidad 08_22591.indd 123 10/03/2015 13:16:46 UNIDAD 8 12 • 6,7 , 6,75 • 2,816 , 2,96 • 36 . 28,05 13 • (10 2 1,85) 3 3,40 5 27,71 € Pagó 27,71 €. 14 • 7,26 3 5 5 36,30 € 7,26 3 10 5 72,6 € Gastará 36,30 € en 500 km y 72,80 € en 1.000 km. • 1,20 1 0,65 1 0,09 5 1,94 Mide 1,94 m de altura. • (50 2 7) 3 3,75 5 161,25 Carmen obtuvo 161,25 €. 15 • 0,2 1 0,25 5 0,45 kg Pesan 0,45 kg. • 3 3 0,24 5 0,72 kg 3 3 0,05 5 0,15 kg Necesita 0,72 kg de mantequilla y 0,15 kg de cacao. • 0,25 3 10 5 2,5 0,2 3 10 5 2 Necesita 2,5 kg de azúcar y 2 kg de harina. • 0,24 3 100 5 24 Gastó menos de 25 kg de mantequilla (gastó 24 kg). 0,05 3 100 5 5 Gastó 5 kg de cacao. • 8 3 (0,2 1 0,24) 5 3,52 8 3 (0,25 1 0,05) 5 2,4 3,52 2 2,4 5 1,12 La harina y la mantequilla pesan 1,12 kg más. Demuestra tu talento 16  Expresamos cada fracción en forma de decimal y multiplicamos los decimales obtenidos. • 0,7 3 0,2 5 0,14 • 0,03 3 0,5 5 0,015 • 0,9 3 0,06 5 0,054 Notas Competencias • Competencia social y cívica. Realice en común, aprovechando el contexto de la actividad 15, un debate sobre temas relacionados con esta competencia: la importancia de una dieta sana, los derechos y deberes de los trabajadores, la necesidad de un consumo responsable… Pida a los alumnos que comenten sus ideas sobre estos temas y enuncien conductas positivas. 53
  • 54.
    Revisar una factura Despuésde la olimpíada de primavera, el colegio organiza siempre una pequeña celebración para entregar los premios. Sergio, el director, está revisando los artículos que pidieron para la fiesta y la factura que le han enviado. 1 Observa la factura y resuelve. ¿Cuánto cuestan las botellas de zumo? ¿Cuánto cuestan las de agua? ¿Cuánto costaron las almendras y las patatas? ¿Cuánto costaron los bollitos? ¿Cuál fue el precio total de todos los artículos? Para hallar el precio a pagar hay que multiplicar el precio total por 1,21 ya que tenemos que añadir los impuestos. En la factura del supermercado Sergio ve que pone 174,63 €. ¿Está bien hecha? ¿Por qué? 2 TRABAJO COOPERATIVO. Resuelve con tu compañero. Para el año que viene, en el colegio han pensado comprar algunas cosas más para la fiesta. Quieren comprar 5 unidades más de cada artículo y cuentan con 200 € para la fiesta. ¿Tendrán bastante dinero? SABER HACER Artículo Unidades Precio unidad Botella de zumo 1,5 ℓ 10 2,75 Botella de agua 2 ℓ 30 0,79 Bolsa de almendras 8 3,37 Bolsa de patatas 20 1,42 Bolsa de bollitos 12 4,35 124 ES0000000024590 663006-Unidad 08_22591.indd 124 10/03/2015 13:16:49 Propósitos •  Desarrollar la competencia matemática resolviendo problemas de la vida cotidiana. •  Repasar contenidos clave. Actividades pág. 124 1 •  2,75 3 10 5 27,5   0,79 3 30 5 23,7  Zumo: 27,50 €.  Agua: 23,70 €. •  8 3 3,37 1 20 3 1,42 5 55,36 Almendras y patatas: 55,26 €. 4,35 3 12 5 52,2  Bollitos: 52,20 €. •  27,5 1 23,7 1 26,96 1 28,4 1 1 52,2 5 158,76  Precio total: 158,76 €. •  158,76 3 1,21 5 192,0996 € La factura no está bien hecha porque el total a pagar por el colegio, redondeando, es 192,10 €. 2 5 3 (2,75 1 0,79 1 3,37 1   1 1,42 1 4,35) 5 63,4  158,76 1 63,4 5 222,16 €  No tendrán suficiente con 200 € para la fiesta. Actividades pág. 125 1 •  300.089 •  6.100.004 •  2 6 •  3 8 •  9,02 •  19,015 2 •  3 CM 1 6 UM 1 7 C 1 1 D 1  1 5 U 5 300.000 1 6.000 1  1 700 1 10 1 5  Trescientos seis mil setecientos quince. •  8 U. de millón 1 1 CM 1 2 C 1  1 4 U 5 8.000.000 1 100.000 1  1 200 1 4  Ocho millones cien mil doscientos cuatro. •  7 U 1 9 d 1 4 c 5  5 7 1 0,9 1 0,04  7 unidades y 94 centésimas. •  1 D 1 2 U 1 7 d 1 6 m 5  5 10 1 2 1 0,7 1 0,006   12 unidades y 706 milésimas. Desarrollo de la competencia matemática •  En esta página los alumnos aplican las operaciones con decimales estudiadas en la unidad para resolver una situación de la vida real.  Es una situación próxima a ellos y que les resultará interesante. A la hora de abordar el trabajo cooperativo, pida a los alumnos que pongan por escrito cuál va a ser su modo de trabajo: qué van a calcular, por qué   y cómo van a realizar esos cálculos. Pídales también que calculen cuánto dinero necesitarán para la fiesta o cuántas unidades más de cada producto (o de algún producto en concreto) podrían comprar con el presupuesto   de 200 €. Inteligencia intrapersonal 54
  • 55.
    4 Elimina losceros que puedas y calcula cada división exacta. 2.500 : 50 63.000 : 900 3.600 : 600 28.000 : 40 5 Completa en tu cuaderno. 2 7 , 2 5 10 . 10 3 , 1 6 Compara. 11 5 2 4 31 8 15 7 3 7 Aproxima al orden indicado. Unidades 9,7 6,8 3,2 9,4 Décimas 9,36 8,21 7,48 Centésimas 5,132 9,278 1 Escribe con cifras. Trescientos mil ochenta y nueve. Seis millones cien mil cuatro. Dos sextos. Tres octavos. Nueve unidades y dos centésimas. Diecinueve coma cero quince. 2 Descompón cada número y escribe cómo se lee. 306.715 7,94 8.100.204 12,706 3 Calcula. 39.871 1 7.878 99.013 : 8 36.890 2 4.996 47.126 : 54 372 3 875 32.630 : 65 8 En salto de longitud, Jonás saltó 4,75 m, Elena 4,8 m y Lourdes 4,72 m. ¿Cuántos metros saltó el primer clasificado más que el último? 9 Los tres cuartos de una clase de 24 alumnos fueron a una ruta de senderismo. De ellos, la mitad eran chicas. ¿Cuántas chicas fueron a la ruta de senderismo? 10 En 4.º A todos deben leer un libro. Ana ha leído ya dos quintos, Silvia dos sextos y Juan tres quintos. ¿Quién ha leído más? 11 Al revisar 975 teléfonos móviles, se desecharon 14 por defectos. El resto se envió en paquetes de 31 teléfonos. ¿Cuántos paquetes se enviaron? 12 Los 12.000 socios de un club van a un partido en autobuses de 52 plazas. Cada uno cuesta 500 €. ¿Cuánto dinero han pagado? 13 ¿Cuánto cuestan 1.000 bolígrafos a 2,75 € cada uno? Problemas REPASO ACUMULATIVO 8 125 ES0000000024590 663006-Unidad 08_22591.indd 125 10/03/2015 13:16:50 UNIDAD 8 3 • 47.749 • c 5 12.376, r 5 5 • 31.894 • c 5 872, r 5 38 • 325.500 • c 5 502 4 • 50 • 70 • 6 • 700 5 R. M. •  2 7 , 2 5 •  5 10 . 1 10   •  2 3 , 1 6 •  11 5 . 2 •  4 . 31 8 •  15 7 , 3 7 • 10 • 7 • 3 • 9 • 9,4 • 8,2 • 7,5 • 5,13 • 9,28 8 4,8 2 4,72 5 0,08 Saltó 0,08 m más. 9 3 4 de 24 5 18; 18 : 2 5 9 Fueron a la ruta 9 chicas. 10 2 6 , 2 5 , 3 5 Ha leído más Juan. 11 975 2 14 5 961 961 : 31 5 31 Se enviaron 31 paquetes. 12 12.000 : 52 c 5 230, r 5 40 Necesitan 231 autobuses. 231 3 500 5 115.500 Han pagado 115.500 €. 13 2,75 3 1.000 5 2.750 Cuestan 2.750 €. Notas Repaso en común • Pida a los alumnos que realicen las actividades propuestas en esta página de forma individual y anoten aquellas en las que han tenido alguna dificultad para resolverlas. Comente con ellos por qué les han resultado más difíciles, y refuerce esas carencias resolviéndolas en común en la pizarra y proponiendo algunas más para asentar bien esos contenidos y avanzar con seguridad. 55
  • 56.
    En el ambulatoriohan representado en un gráfico de barras el número de personas atendidas del lunes al miércoles. Fíjate en cómo se interpreta. Gráficos de barras de tres características Tratamiento de la información 1 Observa el gráfico de arriba y contesta. ¿Cuántos adultos fueron atendidos el lunes? ¿Y niños? ¿Qué grupo fue el más numeroso el miércoles? ¿Y el lunes? ¿En qué días se atendió a más de 30 mayores? 2 Copia y completa el gráfico con los datos de las piezas de fruta que han comido esta semana tres amigos. Luis: 20 peras, 12 naranjas y 8 manzanas. Jon: 12 peras, 4 naranjas y 16 manzanas. María: 8 peras, 4 naranjas y 16 manzanas. Niños Adultos Mayores Número de personas Eje horizontal El miércoles atendieron a 50 mayores. Eje vertical Miércoles Martes Lunes 0 10 20 30 405 15 25 35 45 50 El martes, los adultos fueron el grupo más numeroso. Pera Naranja Manzana 24 20 16 12 8 4 0 Númerodepiezas Luis Jon María 126 ES0000000024590 663006-Unidad 08_22591.indd 126 10/03/2015 13:16:51 Gráficos de barras de tres característicasPropósitos •  Interpretar gráficos de barras   de tres características. •  Representar datos en gráficos   de barras de tres características. Sugerencias didácticas Para explicar. Haga que los alumnos observen el gráfico. Explíqueles cuál es el significado de cada barra de color y señale que para cada día tenemos información de las tres características. Trabaje en común algunas preguntas de interpretación, por ejemplo: ¿Cuántos niños fueron atendidos el martes? ¿En qué día atendieron a más adultos? ¿Entre   qué dos días aumentó el número   de adultos atendidos? Comente que para representar los gráficos debemos levantar una barra de la altura oportuna para cada característica. Trabaje la interpretación con el gráfico obtenido. Deje que los alumnos realicen por   sí solos el trabajo de recopilación   de datos y representación. Después, verifique que todos han obtenido   la misma gráfica e interprete,   de forma colectiva, los casos propuestos en el cuadro. 1 •  Adultos el lunes: 20.  Niños el lunes: 15. •  El miércoles: mayores.  El lunes: mayores. •  El lunes y miércoles. 2 3 a 5   R. L. Otras actividades •  Haga grupos de dos o tres alumnos y pídales que se fijen en el gráfico   del cuadro informativo y escriban varias frases que sean correctas a partir   de los datos representados. Por ejemplo: –  El día que menos niños se atendieron en consulta fue el miércoles. –  El día que más adultos se atendieron en consulta fue el martes. –  Del lunes al martes disminuyó el número de niños atendidos. Comente después algunas de ellas en común. Inteligencia espacial 20 16 12 8 4 0 Luis Jon María 56
  • 57.
    UNIDAD 8 3 Hazuna encuesta en clase y completa la tabla en tu cuaderno. Para cada día de la semana, pregunta cuántas personas han dormido muy bien, bien o regular, y apúntalo en la tabla. 4 Copia y completa el gráfico con los resultados de la encuesta. 5 Observa el gráfico que has construido y contesta. ¿Cuántos alumnos durmieron muy bien el lunes? ¿Cuántos durmieron regular el miércoles? ¿Qué día hubo más alumnos que durmieran bien? ¿Qué día es el que menos alumnos durmieron muy bien? ¿Cuál fue la respuesta más común el miércoles? ¿Cuál fue la menos común el martes? ¿Qué tipo de respuesta fue la más común en los cuatro días? Muy bien Bien Regular Lunes Martes Miércoles Jueves 5 ¡No olvides anotar tu voto! 8 Muy bien Bien Regular Númerodealumnos Lunes MiércolesMartes Jueves 18 16 14 12 10 8 6 4 2 0 127 ES0000000024590 663006-Unidad 08_22591.indd 127 10/03/2015 13:16:53 Notas Competencias •  Competencia digital. Comente con los alumnos que muchas informaciones se transmiten mediante gráficos y, por tanto, es muy importante saber interpretarlos y representarlos correctamente. Con la ayuda de programas informáticos, puede realizar (o pedir a los alumnos que lo hagan) distintos gráficos de barras de tres características para trabajar los contenidos vistos en la doble página. 57
  • 58.
    Tiempo y dinero9 Contenidosde la unidad SABER MEDIDA • El reloj digital. • Unidades de tiempo. • Problemas con unidades de tiempo y dinero. SABER HACER MEDIDA • Lectura y escritura de horas en el reloj digital, reconociendo horas antes y después del mediodía. • Cálculo del tiempo transcurrido entre dos horas dadas. • Obtención y representación de la hora que es, dada la hora de inicio y el tiempo transcurrido. • Utilización de las equivalencias entre las distintas unidades de tiempo. • Resolución de problemas de tiempo. • Resolución de problemas donde aparezcan situaciones de compra. RESOLUCIÓN DE PROBLEMAS • Cambio de los datos de un problema para obtener una solución distinta. • Invención de un problema cambiando los datos para que se resuelva según unos cálculos dados.   TAREA FINAL • Programar horarios. SABER SER FORMACIÓN EN VALORES • Valoración de la utilidad de las unidades de tiempo y dinero. • Interés por la resolución de problemas cotidianos donde aparezcan unidades de tiempo y dinero. 58
  • 59.
    BIBLIOTECA DEL PROFESORADO Programacióndidáctica de aula Recursos para la evaluación • Evaluación de contenidos. Unidad 9: pruebas de control B y A. • Evaluación por competencias. Prueba 9. •  Rúbrica. Unidad 9. Enseñanza individualizada • Plan de mejora. Unidad 9. • Programa de ampliación. Unidad 9. Proyectos de trabajo cooperativo • Proyecto del segundo trimestre. Recursos complementarios • Fichas para el desarrollo de la inteligencia. • Operaciones y problemas. Aprendizaje eficaz • Técnicas de estudio y presentación de exámenes. Proyectos interdisciplinares • Programa de Educación en valores. • Programa de Educación emocional. • Inteligencias múltiples. RECURSOS DIGITALES LibroMedia • Unidad 9: actividades y recursos. MATERIAL DE AULA Láminas OTROS MATERIALES DEL PROYECTO Cuaderno del alumno • Segundo trimestre. Unidad 9. Solución de problemas. Método DECA SUGERENCIA DE TEMPORALIZACIÓN Enero MarzoFebrero ES0000000024590 663006_Matematicas_4_GRAZ_24259 PRIMARIA PRIMARIA Matemáticas PRIMARIA ANDALUCÍAMatemáticas ANDALUCÍA Matemáticas ANDALUCÍA ES0000 000024 590 663006 _Matem aticas_4_GRA Z_2425 9.indd 1 04/03/2 015 11:21:19 ES0000000024593 663039_Cdno_Matematicas_4-2_22732 PRIMARIA Matemáticas Segundo trimestre Matemáticas Segundo trimestre PRIMARIA CUADERNO CUADERNO ES0000000024593 663039_Cdno_Matematicas_4-2_22732.indd 1 19/02/2015 16:56:18 59
  • 60.
    9 Tiempo ydinero Visita a un parque eólico Hoy los alumnos de 4.º de Primaria visitarán un parque eólico. La profesora les muestra algunas fotos y les explica cómo funcionan esos enormes molinos de viento. Todos están impresionados de su tamaño. Después, la profesora reparte a cada uno el horario. –¿Podremos hacernos una foto con los molinos? –pregunta María. –¡Seguro que sí! –contesta la profesora. VISITA A UN PARQUE EÓLICO 9 : 00 Salida 9 : 45 Charla informativa 10 : 30 Visita al parque 14 : 15 Comida 16 : 00 Regreso 128 ES0000000024590 663006-Unidad 09_22592.indd 128 10/03/2015 13:22:44 VISITA A UN PARQUE EÓLICO 9 : 00 Salida 9 : 45 Charla informativa 10 : 30 Visita al parque 14 : 15 Comida 16 : 00 Regreso Propósitos •  Reconocer situaciones reales en las que se utilicen unidades de tiempo. •  Recordar los conceptos básicos necesarios para el desarrollo   de la unidad. Previsión de dificultades •  Algunos alumnos pueden tener dificultad en interpretar las horas, después del mediodía, en un reloj digital y representar estas horas   en un reloj de agujas. Si lo ve necesario, realice varias actividades de este tipo para subsanar estos posibles errores. •  Los alumnos pueden tener dificultad para elegir la operación adecuada (multiplicación o división) al resolver problemas con unidades de tiempo. Realice numerosas actividades   en uno y otro sentido. Trabajo colectivo sobre la lámina Haga que un alumno lea la situación planteada y pregunte a los alumnos si han visto alguna vez un parque eólico, dónde lo vieron, cómo son los molinos, etc. A continuación, pídales que realicen las actividades propuestas de forma individual   y corrija los resultados en la pizarra, despejando las dudas que hayan podido surgir. 1 Salida Comida Visita Charla 2 Pasan 45 minutos. 3 La visita comenzó a las 10   y media y terminó a las 12. 4 R. M. Se añade 1 hora y 30 minutos a la hora que comenzó   la visita que fue a las 10 y media. Otras formas de empezar •  Comente con los alumnos las horas más importantes del horario   del colegio: a qué hora entran, a qué hora es el recreo, a qué hora es   la comida, a qué hora se sale... Escríbalas en la pizarra y pregunte a los alumnos si creen que es necesario conocer la hora, por qué creen que lo es, etc. Explique la importancia en nuestra sociedad de tener una medida   de tiempo común para todos. 12 1 2 3 4 567 8 9 10 11 12 1 2 3 4 567 8 9 10 11 12 1 2 3 4 567 8 9 10 11 12 1 2 3 4 567 8 9 10 11 12 1 2 3 4 567 8 9 10 11 12 1 2 3 4 567 8 9 10 11 12 1 2 3 4 567 8 9 10 11 12 1 2 3 4 567 8 9 10 11 12 1 2 3 4 567 8 9 10 11 12 1 2 3 4 567 8 9 10 11 12 1 2 3 4 567 8 9 10 11 12 1 2 3 4 567 8 9 10 11 12 1 2 3 4 567 8 9 10 11 12 1 2 3 4 567 8 9 10 11 12 1 2 3 4 567 8 9 10 11 12 1 2 3 4 567 8 9 10 11 60
  • 61.
    12 1 2 3 4 567 8 9 10 11 1 Copiael reloj en tu cuaderno y representa la hora a la que se realiza cada actividad. Salida … Comida … Visita a la estación … Charla informativa … 2 ¿Cuánto tiempo pasa desde la salida hasta que empieza la charla informativa? 3 La visita a la estación duró 1 hora y 30 minutos. ¿A qué hora terminó? 4 EXPRESIÓN ORAL. Explica cómo has calculado la hora a la que terminó la visita. Lee, comprende y razona La lectura de horas en relojes de agujas y digitales Son las 8 y cuarto de la mañana. Son las 4 y diez de la tarde. 1 Escribe la hora que marca cada reloj. La suma y la resta de decimales 1.º Coloca los números de forma que coincidan en columna las unidades del mismo orden. 2.º Suma o resta como si fueran números naturales y escribe la coma en el resultado debajo de las comas. 2 Coloca los números y calcula en tu cuaderno. 53,19 1 28,67 72,89 1 8,6 49,75 2 27,16 91,34 2 8,7 ¿Qué sabes ya? TAREA FINAL Programar horarios Al final de la unidad programarás los horarios de un gimnasio. Antes, estudiarás las horas, las unidades de tiempo y resolverás problemas. SABER HACER 12 1 2 3 4 567 8 9 10 11 12 1 2 3 4 567 8 9 10 11 12 1 2 3 4 567 8 9 10 11 12 1 2 3 4 567 8 9 10 11 12 1 2 3 4 567 8 9 10 11 14:1508:00 21:3021 :30 8 :00 8 :15 14 :15 16 :10 5 6, 3 9 1 9, 8 6 6, 1 9 7 3, 0 4 2 2 6, 5 7 4 6, 4 7 129 ES0000000024590 663006-Unidad 09_22592.indd 129 10/03/2015 13:22:46 UNIDAD 9 ¿Qué sabes ya? Recuerde con los alumnos la lectura y representación de las horas en relojes analógicos y digitales. Pídales que digan las características de cada uno. Trabaje también la suma y resta de decimales, necesarias para los cálculos con cantidades de dinero. 1 Las 10 y media. Las 5 y diez. Las 2 menos cuarto. Las 8 de la mañana. Las 2 y cuarto de la tarde. Las 9 y media de la noche. 2 •  53,19 1 28,67 5 81,86 •  72,89 1 8,6 5 81,49 •  49,75 2 27,16 5 22,59 •  91,34 2 8,7 5 82,64 Notas Competencias • Comunicación lingüística. Al realizar las actividades propuestas después de la lectura es importante comprobar que los alumnos conocen los términos matemáticos relativos al tiempo y los utilizan correctamente. Anímelos siempre a razonar sus respuestas de forma coherente. • Aprender a aprender. Comente con los alumnos la importancia que tiene asentar bien los conocimientos estudiados para poder avanzar con seguridad. Muestre que en esta unidad van a seguir aprendiendo sobre dos temas que ya conocían: el tiempo y el dinero. 61
  • 62.
    El reloj digital 1Escribe cómo se lee la hora de cada reloj digital como en un reloj de agujas. Piensa si la hora es antes o después del mediodía. 2 Representa en tu cuaderno la hora de cada reloj digital en un reloj de agujas. RECUERDA En un reloj digital, las horas después del mediodía se representan por 13, 14, 15... EJEMPLO La 1 y cinco de la tarde.13:05 17:10 15:40 17:45 20:35 21:50 22:55 13:05 5:10 15:20 10:35 20:40 23:45 17:10 EJEMPLO La ruta del autobús escolar comienza a las 8 de la mañana y termina a las 9. Observa cómo se expresan las horas de las 8 a las 9 en un reloj digital. 8:00 Las 8 8:05 Las 8 y cinco 8:10 Las 8 y diez 8:15 Las 8 y cuarto 8:20 Las 8 y veinte 8:25 Las 8 y veinticinco 8:30 Las 8 y media 8:35 Las 9 menos veinticinco 8:40 Las 9 menos veinte 8:45 Las 9 menos cuarto 8:50 Las 9 menos diez 8:55 Las 9 menos cinco 9:00 Las 9 12 1 2 3 4 567 8 9 10 11 12 1 2 3 4 567 8 9 10 11 12 1 2 3 4 567 8 9 10 11 130 ES0000000024590 663006-Unidad 09_22592.indd 130 10/03/2015 13:22:48 Propósitos •  Interpretar las horas antes   y después del mediodía en un reloj digital. •  Representar horas antes y después del mediodía en un reloj digital. •  Resolver problemas con tiempos. Sugerencias didácticas Para explicar. Lea la situación planteada en el cuadro informativo   y muestre a los alumnos cómo   se expresan las horas de las 8   a las 9 en un reloj digital. Comente   en especial los casos a partir   de «y media» ya que son los más nuevos para los alumnos. Señale   que, cuando el número de minutos   es mayor que 30, es necesario referirse a la hora siguiente. Muestre que, cuando la cifra de las horas es mayor de 12, nos estamos refiriendo a horas después del mediodía. Para reforzar. Diga una hora   (o escríbala en la pizarra) y pida   a varios alumnos que salgan   y dibujen en un reloj digital la hora   que sería un cuarto de hora, media hora, tres cuartos de hora, 1 hora,   1 hora y cuarto… antes o después. Actividades 1 •  La 1 y cinco de la tarde. •  Las 5 y diez de la mañana. •  Las 3 y veinte de la tarde. •  Las 11 menos veinticinco   de la mañana. •  Las 9 menos veinte de la tarde. •  Las 12 menos cuarto   de la noche. 2 Otras actividades •  Proponga a los alumnos construir un reloj digital con cartulina.   Para ello, indíqueles que hagan dos tiras largas de unos 2 cm de ancho   y que escriban en vertical en una tira las horas (0, 1, 2, …, 23)   y en la otra los minutos (00, 05, 10, …, 55). Además, harán un rectángulo de 10 3 5 cm, escribirán   en el centro el signo : y dibujarán dos ventanillas,   perforando las líneas horizontales para introducir   las tiras anteriores. •  Utilice este reloj como apoyo al realizar las actividades   de escritura y lectura de horas, cálculo de tiempos   transcurridos, etc. 10 11 12 13 14 15 20 25 30 35 17 18 19 45 50 55 15    :    40 12 1 2 3 4 567 8 9 10 11 12 1 2 3 4 567 8 9 10 11 12 1 2 3 4 567 8 9 10 11 12 1 2 3 4 567 8 9 10 11 12 1 2 3 4 567 8 9 10 11 12 1 2 3 4 567 8 9 10 11 62
  • 63.
    14:1508:00 21:30 9 3 Calcula yescribe en tu cuaderno qué hora marcará cada reloj digital. 16:35 2 horas y 20 minutos después. 3 horas y media después. 20:45 3 horas y 20 minutos antes. 4 horas y media antes. Problemas 4 Resuelve. Hoy comienzan las fiestas del barrio y Carlota y sus amigos leen las actividades propuestas. ¿Qué actividades están propuestas por la mañana? ¿Y por la tarde? ¿Cuánto tiempo dura el guiñol? ¿Y los pintacaras? ¿Cuánto tiempo dura cada actividad programada por la tarde? Carlota quiere ir al guiñol y luego a los pintacaras. ¿Podrá ir y volver a su casa, que está a 10 minutos del lugar donde se hace el guiñol? Invéntate una actividad que se realice por la tarde y que dure 1 hora y media. Escribe a qué hora comienza y termina. Resta 11 a un número: primero resta 10 y luego resta 1 32 2 11 208 2 11 3.176 2 11 47 2 11 384 2 11 4.185 2 11 58 2 11 415 2 11 6.084 2 11 CÁLCULO MENTAL 147 137 136 2 10 2 1 2 11 HAZLO ASÍ 14:25 3 horas y 15 minutos después El reloj marcará: 17:40 3 horas después 14 1 3 5 17 15 minutos después 25 1 15 5 40 14:25 17:40 COMIENZA TERMINA Guiñol 10:30 11:45 Pintacaras 12:10 13:30 Payasos 17:15 19:30 Teatro 21:00 22:45 131 ES0000000024590 663006-Unidad 09_22592.indd 131 10/03/2015 13:22:49 UNIDAD 9 3   16:35 • • • • 4 • Por la mañana: guiñol y pintacaras. Por la tarde: payasos y teatro. • El guiñol dura 1 hora y 15 minutos. Los pintacaras duran 1 hora y 20 minutos. • Los payasos duran 2 horas y 15 minutos. El teatro dura 1 hora y 45 minutos. • Carlota tarda 20 minutos en ir y volver a su casa. Si sale del guiñol a las 11:45 más los 20 minutos que tarda en ir y volver, a las 12:05 ya estará, luego sí puede ir y volver a su casa. • R. M. Carrera ciclista: comienza a las 18:30 y termina a las 20:00. Cálculo mental •  21 •  197 •  3.165 •  36 •  373 •  4.174 •  47 •  404 •  6.073 Notas Otras actividades •  Pida a los alumnos que hagan el horario de un día de colegio, escribiendo cada hora en un reloj digital. En él deben reflejar, además de las horas a las que tienen cada clase o actividad extraescolar, las horas a las que suelen realizar otras actividades diarias como: levantarse, desayunar, salir de casa hacia el colegio, comer, merendar, hacer los deberes, jugar, ver la televisión, ducharse, acostarse, etc. Haga una puesta en común y plantee ejercicios de estimación y de cálculo de tiempos transcurridos: el tiempo que dura una actividad o el que pasa entre dos actividades dadas… 20:45 17:25 18:55 20:05 16:15 Inteligencia interpersonal 63
  • 64.
    Unidades de tiempo 1Calcula en tu cuaderno cuántos meses son. 2 trimestres 3 trimestres 4 trimestres 2 cuatrimestres 4 cuatrimestres 5 cuatrimestres 3 semestres 4 semestres 6 semestres 2 ¿Cuántos años son? Calcula en tu cuaderno. 2 lustros 3 lustros 5 lustros 3 décadas 5 décadas 7 décadas 3 siglos 4 siglos 6 siglos 3 Calcula. Recuerda que el año tiene 365 días y que un año tiene 12 meses. Para medir el tiempo utilizamos distintas unidades, unas menores que el año y otras mayores. MENORES QUE EL AÑO Un trimestre es 3 meses. Un cuatrimestre es 4 meses. Un semestre es 6 meses. MAYORES QUE EL AÑO Un lustro es 5 años. Una década es 10 años. Un siglo es 100 años. ¿Cuántos trimestres son? 9 meses 15 meses 12 meses 21 meses ¿Cuántos lustros son? 10 años 20 años 15 años 30 años ¿Cuántos cuatrimestres son? 12 meses 24 meses 16 meses 32 meses ¿Cuántas décadas son? 20 años 60 años 50 años 80 años ¿Cuántos semestres son? 18 meses 30 meses 24 meses 42 meses ¿Cuántos siglos son? 200 años 500 años 400 años 900 años 132 ES0000000024590 663006-Unidad 09_22592.indd 132 10/03/2015 13:22:54 Propósitos •  Conocer la equivalencia entre   las distintas unidades de tiempo. •  Resolver situaciones reales con unidades de tiempo. Sugerencias didácticas Para explicar. Pida a los alumnos   que observen el cuadro y recuérdeles los días y los meses que tiene un año. Exprese que hay unidades de tiempo menores que el año y nómbrelas escribiendo su equivalencia en la pizarra. Proceda de forma análoga con las unidades de tiempo mayores que el año. Para reforzar. Agrupe a los alumnos   y pídales que preparen, en forma   de mural, de línea del tiempo, de esquema, etc., un resumen donde aparezcan todas las unidades   de tiempo y sus equivalencias. Actividades 1 •  6 meses •  8 meses •  9 meses •  16 meses •  12 meses •  20 meses •  18 meses •  24 meses •  36 meses 2 •  10 años •  30 años •  15 años •  50 años •  25 años •  70 años • 300 años • 400 años •  600 años 3 •  3 trimestres •  2 lustros •  4 trimestres •  3 lustros •  5 trimestres •  4 lustros •  7 trimestres •  6 lustros •  3 cuatrimestres •  2 décadas •  4 cuatrimestres •  5 décadas •  6 cuatrimestres •  6 décadas •  8 cuatrimestres •  8 décadas •  3 semestres •  2 siglos •  4 semestres •  4 siglos •  5 semestres •  5 siglos •  7 semestres •  9 siglos Otras actividades •  Pregunte a los alumnos cuántos y cuáles son los meses del año y escríbalos ordenados en la pizarra. Calcule de forma colectiva cuántos trimestres   y semestres hay en un año, y qué meses forman cada uno de ellos. Hágales observar que el curso escolar no comienza en enero, por lo que el primer trimestre de curso no coincide con el primer trimestre del año. •  Nombre algunas fechas señaladas del año para que los alumnos digan   de qué trimestre o semestre son. Por ejemplo: el día de Reyes,   el comienzo de las vacaciones de verano o Navidad, el cumpleaños   de cada niño… 64
  • 65.
    9 Lee y contesta. Mariole dice a su amiga Lorena: «Ayer, mi hermano pequeño tenía 8 años y el año que viene cumplirá 10». ¿Qué día cumple los años el hermano de Mario? Razona tu respuesta. RAZONAMIENTO 4 Lee y calcula. Nuria hizo un curso de fotografía durante un cuatrimestre. ¿Cuántos días duró el curso? Alfredo viaja a Sevilla cada 90 días. ¿Cada cuántos meses va a Sevilla? Problemas 5 Fíjate en el año en el que se inventó cada aparato y calcula. ¿Cuántos años hace que se inventó cada aparato? ¿Cuántos siglos y años son? ¿Cuántos siglos y años pasaron desde la invención de los prismáticos hasta la invención del teléfono? ¿Cuántas décadas y años son? ¿Cuántos años pasaron desde la invención del microscopio hasta la invención de los prismáticos? ¿Cuántos lustros y años son? 6 Resuelve. Fabiana compra una finca y la va a pagar en 10 años, pagando la misma cuota cada trimestre. ¿Cuántas cuotas pagará en un año? ¿Y en un lustro? ¿Cuántas cuotas pagará en total en los 10 años? En cada cuota Fabiana paga 545 €. ¿Cuánto pagará Fabiana por la finca? MICROSCOPIO Año 1590 PRISMÁTICOS Año 1608 PRESTA ATENCIÓN Los meses tienen 30 o 31 días, salvo febrero que tiene 28 o 29. Al hacer cálculos se consideran todos los meses de 30 días. TELÉFONO Año 1876 133 ES0000000024590 663006-Unidad 09_22592.indd 133 10/03/2015 13:22:57 UNIDAD 9 4 • 4 3 30 5 120 El curso duró 120 días. • 90 : 30 5 3 Cada 3 meses viaja a Sevilla. 5 • Teléfono Año actual 2 1876 Ejemplo: 2.016 2 1.876 5 140 años 5 5 1 siglo y 40 años Microscopio 2.016 2 1.590 5 426 años 5 5 4 siglos y 26 años Prismáticos 2.016 2 1.608 5 408 años 5 5 4 siglos y 8 años • 1.876 2 1.608 5 268 años 5 5 26 décadas y 8 años • 1.608 2 1.590 5 18 años 5 5 3 lustros y 3 años 6 • 12 : 3 5 4 5 3 4 5 20 Pagará 4 cuotas al año y 20 cuotas en un lustro. • 4 3 10 5 40 Pagará 40 cuotas en 10 años. • 40 3 545 5 21.800 Pagará 21.800 € por la finca. Razonamiento El hermano de Mario cumple los 9 años el 1 de enero. De esta forma, el día 31 de diciembre tenía 8 años y el 1 de enero del próximo año cumplirá 10 años. Notas Otras actividades • Copie en la pizarra la siguiente sopa de letras. Pida a nueve alumnos que rodeen cada uno una unidad de tiempo. Al final, pida a los alumnos que ordenen las nueve unidades de mayor a menor tiempo, que definan cada unidad relacionándola con otra y que inventen una oración con cada unidad. Por último, haga una puesta en común con las propuestas hechas. T R I M E S T R E A O S P I R E A O D Q L D A N O M E S I E B E H U D E A T O H U C I T O S I G L O S A Ñ O L T N E A R I D F R A R O D I A E A L S I E P M O T 65
  • 66.
    Problemas con unidadesde tiempo y dinero 1 ¿Cuánto dinero hay? Exprésalo con un número decimal. 2 Escribe el menor número posible de monedas y billetes para expresar cada precio. RECUERDA Hay monedas de 1, 2, 5, 10, 20 y 50 céntimos y de 1 € y 2 €. Hay billetes de 5, 10, 20, 50, 100, 200 y 500 €. EJEMPLO 18,35 Billetes: 1 de 10 € y 1 de 5 €. Monedas: 1 de 2 €, 1 de 1 €… 18,35 € 130,84 € 21,75 € 265,90 € Alejandra quiere comprar un conjunto de muebles para el jardín cuyo precio es de 879,99 €. En su cartera lleva estos billetes y monedas. ¿Cuánto dinero le sobra? Billetes 500 1 200 1 100 1 50 1 20 1 10 1 5 5 885 € Monedas 50 1 20 5 70 céntimos 5 0,70 € Dinero que tiene Dinero que le sobra 8 8 5 1 0, 7 0 8 8 5, 7 0 8 8 5, 7 0 2 8 7 9, 9 9 0 0 5, 7 1 A Alejandra le sobran 5,71 €. 134 ES0000000024590 663006-Unidad 09_22592.indd 134 10/03/2015 13:23:08 Propósitos •  Resolver situaciones reales   con unidades de tiempo y dinero. Sugerencias didácticas Para explicar. Haga que los alumnos lean la situación planteada y observen las monedas y billetes. Recuerde   con ellos todos los billetes y monedas de nuestro sistema monetario. Comente la forma de expresar cantidades de dinero usando   los números decimales y razone   qué operaciones hay que realizar para resolver el problema. Señale a los alumnos que aparte   de operar con decimales a la hora   de calcular pueden también expresar todas las cantidades en céntimos   y operar con los números naturales obtenidos. Para reforzar. Trabaje situaciones de compra reales propuestas por usted o por los propios alumnos. Puede también realizar un pequeño mercadillo en el que los alumnos vendan y compren distintos objetos. Actividades 1 •  3,60 €      •  5,35 €      •  10,65 € 2 •  18,35 €: 1 billete de 10 €,   1 de 5 €, 1 moneda de 2 €,   1 de 1 €, 1 de 0,20 €,   1 de 0,10 € y 1 de 0,05 €. •  21,75 €: 1 billete de 20 €,   1 moneda de 1 €, 1 de 0,50 €, 1 de 0,20 € y 1 de 0,05 €. •  130,84 €: 1 billete de 100 €,   1 de 20 €, 1 de 10 €,   1 moneda de 0,50 €,   1 de 0,20 €, 1 de 0,10 €   y 2 de 0,02 €. •  265,90 €:1 billete de 200 €,  1 de 50 €, 1 de 10 €, 1 de 5 €, 1 moneda de 0,50 €   y 2 de 0,20 €. Otras actividades •  Trabaje de forma colectiva y oral, o de manera manipulativa, el cálculo (mental) de devoluciones de dinero con los siguientes grados de dificultad creciente: –  Hay que pagar una cantidad de céntimos y entregas 1 €. –  Hay que pagar una cantidad de céntimos y entregas 2 € o 5 €. –  Hay que pagar una cantidad de euros y céntimos y entregas el menor número de euros posible (te devuelven solo céntimos). –  Hay que pagar una cantidad de euros y céntimos y entregas el menor billete posible (te devuelven euros y céntimos) 66
  • 67.
    3 Fíjate enlas unidades de los datos y resuelve en tu cuaderno. Irene compra un rotulador y entrega para pagar un billete de 5 €. ¿Cuánto dinero le devuelven? Expresa en céntimos y resuelve: 5 € 5 500 céntimos 500 2 85 5 … céntimos le devuelven. Expresa en euros y resuelve: 85 céntimos 5 0,85 € 5 2 0,85 5 … € le devuelven. Pablo compra un sacapuntas y un cuaderno. – ¿Cuánto se gasta en total? – ¿Cuánto le devolverán si entrega para pagar 4 €? 4 Lee y resuelve. Elena se ha apuntado a natación tres días a la semana. En la tabla aparecen los minutos que estuvo nadando cada día. ¿Cuántos minutos en total nadó Elena esta semana? ¿Cuántas horas y minutos son? La semana pasada Elena nadó durante 165 minutos. ¿Cuánto pagó en total por las clases si 45 minutos cuestan 9 €? 9 3 Fíjate en las unidades de los datos y resuelve en tu cuaderno. Irene compra un rotulador y entrega para pagar un billete de 5 €. ¿Cuánto dinero le devuelven? Expresa en céntimos y resuelve: 5 € 5 500 céntimos 500 2 85 5 … céntimos le devuelven. Expresa en euros y resuelve: 85 céntimos 5 0,85 € 5 2 0,85 5 … € le devuelven. Pablo compra un sacapuntas y un cuaderno. – ¿Cuánto se gasta en total? – ¿Cuánto le devolverán si entrega para pagar 4 €? 4 Lee y resuelve. Elena se ha apuntado a natación tres días a la semana. En la tabla aparecen los minutos que estuvo nadando cada día. ¿Cuántos minutos en total nadó Elena esta semana? ¿Cuántas horas y minutos son? La semana pasada Elena nadó durante 165 minutos. ¿Cuánto pagó en total por las clases si 45 minutos cuestan 9 €? Resta 9 a un número: primero resta 10 y luego suma 1 26 2 9 194 2 9 2.823 2 9 49 2 9 275 2 9 5.414 2 9 67 2 9 578 2 9 7.121 2 9 80 2 9 740 2 9 9.150 2 9 CÁLCULO MENTAL 147 137 138 2 10 1 1 2 9 PRESTA ATENCIÓN Expresa siempre todos los datos en la misma unidad: euros o céntimos. Día Tiempo en minutos Lunes 35 Miércoles 30 Viernes 20 Sacapuntas 65 céntimos Cuaderno 2,45 € Rotulador 85 céntimos 135 ES0000000024590 663006-Unidad 09_22592.indd 135 10/03/2015 13:23:09 UNIDAD 9 3 • 500 2 85 5 415 5 2 0,85 5 4,15 Le devuelven 415 cts. 5 5 4,15 €. •  65 1 245 5 310 cts. 0,65 1 2,45 5 3,10 € Gasta 310 cts. 5 3,10 €. 400 2 310 5 90 cts. 4 2 3,10 5 0,90 € Le devuelven 90 cts. 5 0,90 €. 4 • 35 1 30 1 20 5 85 minutos 5 5 1 hora y 25 minutos Esta semana, Elena nadó 1 hora y 25 minutos. • 165 : 45 c 5 3, r 5 30 La semana pasada, Elena estuvo nadando 3 días durante 45 minutos y otro día 30 minutos, luego pagará: 4 3 9 5 36 €. Cálculo mental •  17 •  185 •  2.814 •  40 •  266 •  5.405 •  58 •  569 •  7.112 •  71 •  731 •  9.141 Notas Competencias •  Competencia social y cívica. La situación de la actividad 4 permite, de manera sencilla, suscitar un debate en clase sobre diferentes aspectos relacionados con esta competencia. Puede comentar con ellos la importancia de la actividad física para nuestra salud, el empleo del tiempo libre de forma constructiva, la necesidad de aprovechar las clases al máximo, el ejercicio de nuestros derechos y deberes como consumidores… 67
  • 68.
    Resuelve cada problemay después cambia dos datos para obtener otra solución. 1 En la furgoneta de Gonzalo se puede cargar un máximo de 1.000 kilos. Gonzalo tiene que cargar un paquete de 275 kilos, otro de 450 kilos y el tercero de 300 kilos. ¿Podrá cargar los tres paquetes juntos en su furgoneta? 2 Laura va a hacer un mural pegando postales de paisajes. Laura necesita 18 postales y ha comprado 5 sobres con 3 postales cada uno. ¿Tendrá Laura suficientes postales para hacer el mural? 3 Javier tiene en su huerto 5 filas de manzanos con 12 manzanos cada uno y 7 filas de perales con 15 perales cada uno. ¿Tiene Javier en su huerto más de 200 árboles frutales? 4 En el restaurante de Paula hay 15 mesas. Paula tiene 100 flores y quiere poner en cada mesa un jarrón con 15 flores. ¿Tendrá suficientes flores para todas las mesas? Vamos a leer el problema y cambiar dos datos para obtener otra solución. Los alumnos de 3.º y 4.º han preparado una función de teatro y la van a representar en un colegio cercano. Van 29 alumnos de 3.º, 38 de 4.º y 6 monitores. Para el traslado, han alquilado un autocar de 70 plazas. ¿Podrán ir todos juntos en el autocar? Si sumamos los que van, necesitan: 29 1 38 1 6 5 73 plazas, luego no pueden ir todos en el autocar. Para obtener otra solución, es decir, conseguir que todos vayan en el autocar, la suma de los tres datos ha de ser menor o igual que 70. Como tenemos que cambiar dos datos del problema, un posible problema sería: Los alumnos de 3.º y 4.º han preparado una función de teatro y la van a representar en un colegio cercano. Van 27 alumnos de 3.º, 36 de 4.º y 6 monitores. Para el traslado, han alquilado un autocar de 70 plazas. ¿Podrán ir todos juntos en el autocar? Comprueba que este problema tiene otra solución. Cambiar datos para obtener una solución distinta Solución de problemas 136 ES0000000024590 663006-Unidad 09_22592.indd 136 10/03/2015 13:23:11 Propósitos •  Cambiar los datos de un problema para obtener otra solución. Sugerencias didácticas Para explicar. Haga que los alumnos lean el problema propuesto y comente que para que la solución sea distinta tenemos que conseguir que puedan   ir todos en el autocar. Muestre que existen muchos posibles cambios   y que en el ejemplo resuelto aparece uno solo de ellos. Pídales que aporten algunos más. Señale la necesidad   de comprobar que el nuevo problema que generan tiene una solución diferente. Actividades 1 275 1 450 1 300 5 1.025  No podrá cargarlos.  R. M. Gonzalo tiene que cargar   un paquete de 275 kg, otro   de 450 kg y el tercero de 200 kg. 2 5 3 3 5 15  No tendrá suficientes postales.  R. M. Laura necesita 18 postales   y ha comprado 5 sobres   de 4 postales cada uno. 3 5 3 12 1 7 3 15 5 165  Tiene menos de 200 frutales.  R. M. Javier tiene en su huerto   9 filas de manzanos con 15 manzanos cada uno y 7 filas de perales con 20 perales cada uno. 4 15 3 15 5 225  No tiene flores suficientes.  R. M. En el restaurante de Paula hay 15 mesas. Paula tiene   260 flores y quiere poner en cada mesa 15 flores. 5 45 cm 1 65 cm 1 70 cm 5 5 180 cm  No tiene suficiente cinta.  R. M. Lucía tiene 165 cm de roja, 96 cm de verde y 125 cm   de amarilla. 6 2 3 6 1 3 3 12 5 48  No podrá hacer las rosquillas.  R. M. Alberto tiene 8 cartones   de 10 huevos cada uno   y 4 cartones de 12 huevos. Otras actividades •  Proponga a los alumnos problemas similares a los propuestos   en esta página para que resuelvan de forma individual en sus cuadernos.   Una vez resueltos haga que varios alumnos expongan al resto de la clase   su problema y realice una puesta en común con las diversas propuestas.  Por ejemplo:   Luis puede almacenar en su granja un total de 1.000 kg de pienso.   Hoy le han traído 25 sacos de 15 kg cada uno, 15 sacos de 20 kg cada uno  y 15 sacos de 30 kg cada uno. ¿Podrá almacenar en su granja todo   el pienso? 68
  • 69.
    Cambia los datosmarcados en rojo para que la solución del problema sea la que se indica. Después, escribe el nuevo problema en tu cuaderno. 1 Un pabellón de baloncesto tiene capacidad para 1.500 personas. El primer día que se pusieron en venta las entradas, se vendieron 489, el segundo día, 525, y el tercer día, 350. ¿Cuántas entradas quedaron por vender? 2 Miguel tiene en su frutería 4 cajas de manzanas rojas de 13 kilos cada una y 3 cajas de manzanas verdes de 17 kilos cada una. Ha tenido que tirar 15 kilos de manzanas por estar estropeadas. ¿Cuántos kilos de manzanas le quedan a Miguel? 3 Adela reparte en partes iguales 20 gafas rojas, 14 azules y 18 grises en partes iguales entre 2 expositores. ¿Cuántas gafas coloca en cada expositor? 9 Resuelve cada problema. Después, cambia el valor de tres o más datos para obtener otra solución y escribe el nuevo problema. 5 Para hacer un trabajo manual, Lucía necesita 3 m de cinta. Tiene 45 cm de cinta roja, 65 cm de cinta verde, 70 cm de cinta azul y 25 cm de cinta amarilla. ¿Tendrá suficiente cinta? Recuerda que 1 m 5 100 cm. 6 Hoy, Alberto va a hacer rosquillas en su pastelería. En la receta ve que necesita 52 huevos. Alberto tiene 2 cartones de 6 huevos cada uno y 3 cartones de 12 huevos cada uno. ¿Podrá Alberto hacer las rosquillas? 7 En las rebajas, Sofía compró 4 camisetas a 15 € cada una, 3 camisas a 19 € cada una y 2 cinturones a 10 € cada uno. ¿Tuvo suficiente para pagar con 100 €? 8 Para celebrar su cumpleaños, Sandra compra una bolsa con 15 globos rojos, una con 35 globos azules, una con 20 globos verdes y otra con 10 globos amarillos. El total de globos lo reparte en partes iguales entre 5 mesas. ¿Podrá poner 16 globos en cada mesa? 9 Luisa pesa 20 kg, Antonio 23 kg, Sara 4 kg más que Antonio y Silvia 2 kg menos que Luisa. ¿Pesan más de 110 kg todos juntos? INVENTA TUS PROBLEMAS Cambia los datos marcados en rojo para que la solución del problema sea la que se indica. Después, escribe el nuevo problema en tu cuaderno. 1 Un pabellón de baloncesto tiene capacidad para 1.500 personas. El primer día que se pusieron en venta las entradas, se vendieron 489, el segundo día, 525, y el tercer día, 350. ¿Cuántas entradas quedaron por vender? 2 Miguel tiene en su frutería 4 cajas de manzanas rojas de 13 kilos cada una y 3 cajas de manzanas verdes de 17 kilos cada una. Ha tenido que tirar 15 kilos de manzanas por estar estropeadas. ¿Cuántos kilos de manzanas le quedan a Miguel? 3 Adela reparte en partes iguales 20 gafas rojas, 14 azules y 18 grises en partes iguales entre 2 expositores. ¿Cuántas gafas coloca en cada expositor? 10 1 6 1 12 5 28 28 : 2 5 14 15 3 4 5 60 18 3 3 5 54 60 1 54 2 11 5 103 598 1 425 1 390 5 1.413 1.500 2 1.413 5 87 137 ES0000000024590 663006-Unidad 09_22592.indd 137 10/03/2015 13:23:12 UNIDAD 9 7 4 3 15 1 3 3 19 1 2 3 10 5 137 No tuvo suficiente. R. M. Sofía compra 2 camisetas a 15 € cada una, 2 camisetas a 19 € cada una y 2 cinturones a 8 € cada uno. 8 15 1 35 1 20 1 10 5 80 80 : 5 5 16 Sí podrá poner 16 globos. R. M. Sandra compra 10 globos rojos, 20 azules, 15 verdes y 8 amarillos. 9 20 1 23 1 27 1 18 5 88 Pesan menos de 110 kg. R. M. Luisa pesa 30 kg, Antonio 45 kg, Sara 9 kg más que Antonio y Silvia 1 kg menos que Luisa. Inventa tus problemas 1 R. M. El primer día se vendieron 598, el segundo día, 425 y el tercer día, 390. 2 R. M. Miguel tiene en su frutería 4 cajas de manzanas rojas de 15 kg cada una y 3 cajas de manzanas verdes de 18 kg cada una. Ha tenido que tirar 11 kg de manzanas por estar estropeadas. 3 R. M. Adela reparte en partes iguales 10 gafas rojas, 6 azules y 12 grises en partes iguales entre 2 expositores. Notas Competencias •  Iniciativa y emprendimiento. La autonomía a la hora de resolver los problemas y el emprendimiento necesario para tomar decisiones sobre la resolución y el proceso a seguir se practican intensivamente en las actividades de invención de problemas. Señale a los alumnos que es muy importante reflexionar sobre los datos que se van a cambiar teniendo en cuenta la solución dada y muestre la importancia de comprobar que el nuevo problema generado se resuelve con esos cálculos. Inteligencia interpersonal 69
  • 70.
    6 Completa losrelojes en tu cuaderno. Suma media hora cada vez. 19:35 ... hasta 21:35 Resta un cuarto de hora cada vez. 20:40 ... hasta 19:25 7 Calcula. ¿Cuántos meses son? 4 trimestres 5 trimestres 3 cuatrimestres 6 cuatrimestres 2 semestres 4 semestres ¿Cuántos años son? 2 lustros 4 lustros 3 décadas 5 décadas 4 siglos 6 siglos 8 Expresa en la unidad que se indica. 93 meses en trimestres. 84 meses en cuatrimestres. 120 meses en semestres. 50 años en lustros. 90 años en décadas. 800 años en siglos. 9 Piensa y escribe. María lleva en la mano tres monedas distintas, todas de un valor mayor que 10 céntimos. Expresa con un número decimal el dinero que puede llevar en la mano. 1 VOCABULARIO. Explica mediante un ejemplo cómo se leen en un reloj digital las horas antes y después del mediodía. 2 Representa en un reloj digital una hora antes del mediodía y otra hora después del mediodía. 3 Representa en un reloj de agujas la hora que marca cada reloj digital. 4 Lee la hora a la que se levantó y se acostó cada niño, y representa cada hora en un reloj digital. 5 ¿Qué hora marcará cada reloj digital? Calcula y completa en tu cuaderno. 2 horas y 30 minutos después 3 horas y 45 minutos después 4 horas y 50 minutos después 2 horas y 15 minutos antes 3 horas y 30 minutos antes 4 horas y 40 minutos antes ACTIVIDADES 21:25 8:15 Me levanté a las 9 y 10 de la mañana y me acosté a las 10 y media de la noche. LUIS ANA Me levanté a las 10 menos 20 de la mañana y me acosté a las 11 menos 10 de la noche. 10:20 2:40 9:35 19:10 22:15 16:45 138 ES0000000024590 663006-Unidad 09_22592.indd 138 10/03/2015 13:23:13 Propósitos •  Repasar los contenidos básicos   de la unidad. Actividades 1 R. L. 2 R. M. Antes del mediodía F 3:25  Después del mediodía F 14:45 3 4 LUIS ANA 5 • •  •  •  • •  6 19:35 F 20:05 F 20:35 F 21:05 F  21:35 F 20:40 F 20:25 F 20:10 F 19:55 F 19:40 F 19:25 7 •  12 meses •  15 meses •  12 meses •  24 meses •  12 meses •  24 meses •  10 años •  20 años •  30 años •  50 años •  400 años •  600 años 8 •  31 trimestres •  21 cuatrimestres •  20 semestres •  10 lustros •  9 décadas •  8 siglos Otras actividades •  Lleve a clase periódicos, forme varios grupos de alumnos y entregue   a cada grupo un periódico para que busquen en él la programación   de televisión. Pregunte a cada grupo a qué hora comienza y termina   un determinado programa (comente que consideren que un programa termina cuando comienza el siguiente, sin tener en cuenta el tiempo   de publicidad) y calcule de forma colectiva en la pizarra la duración de cada uno. A continuación, indique a cada niño que elija un programa   y calcule la duración del mismo. Después, lo dirá a sus compañeros   del grupo y entre todos comprobarán que es correcto. 10:45 13:05 17:55 12:00 19:10 16:45 9:10 9:40 22:30 22:50 12 1 2 3 4 567 8 9 10 11 12 1 2 3 4 567 8 9 10 11 12 1 2 3 4 567 8 9 10 11 12 1 2 3 4 567 8 9 10 11 12 1 2 3 4 567 8 9 10 11 12 1 2 3 4 567 8 9 10 11 70
  • 71.
    12 Resuelve. Guillermo yMicaela consultan las actividades propuestas para este sábado en el club de campo. ¿A qué hora termina la actividad de senderismo? Representa en un reloj digital la hora a la que comienza y termina esta actividad. Guillermo dio un paseo a caballo. El paseo comenzó a las 4 menos cuarto de la tarde. ¿A qué hora terminó? Representa estas horas en un reloj digital. ¿Cuánto tiempo dura la visita a la cueva? Problemas 10 Lee y resuelve. El sábado Ricardo se levantó a las 10 y 20 de la mañana y salió a correr 2 horas y media después. ¿A qué hora salió a correr Ricardo? Irene cogió un autobús a las 5 y media de la tarde. Después de estar circulando 2 horas y cuarto, pararon media hora para tomar un refresco y llegaron a su destino a las 11 y cuarto de la noche. ¿Cuánto tiempo pasó desde que salió el autobús del descanso hasta llegar a su destino? 11 Resuelve. En el pueblo de Jorge se celebra un mercadillo medieval desde hace 80 años. ¿Cuántos años faltan para que el mercadillo cumpla un siglo? ¿Cuántas décadas de antigüedad tiene el mercadillo? 12 Resuelve. Guillermo y Micaela consultan las actividades propuestas para este sábado en el club de campo. ¿A qué hora termina la actividad de senderismo? Representa en un reloj digital la hora a la que comienza y termina esta actividad. Guillermo dio un paseo a caballo. El paseo comenzó a las 4 menos cuarto de la tarde. ¿A qué hora terminó? Representa estas horas en un reloj digital. ¿Cuánto tiempo dura la visita a la cueva? 9 13 Rosana ha cambiado en el banco una moneda de 2 € en monedas del mismo valor. Le han dado más de 20 monedas y menos de 100. ¿Por qué clase de moneda ha cambiado Rosana los 2 €? Demuestra tu talento Senderismo Hora de salida: 8 y media de la mañana. Duración: 3 horas y media. Paseo a caballo Desde las 9 de la mañana hasta las 5 de la tarde. Duración del paseo: 45 minutos. Visita a la cueva Hora de salida: 4 y cuarto de la tarde. Hora de regreso: 8 menos cuarto de la tarde. 139 ES0000000024590 663006-Unidad 09_22592.indd 139 10/03/2015 13:23:15 UNIDAD 9 9 0,20 1 0,50 1 1 5 1,70 0,20 1 0,50 1 2 5 2,70 0,50 1 1 1 2 5 3,50 Puede llevar 1,70 €, 2,70 € o 3,50 €. 10 • Salió a correr a las 12:50 o la 1 menos diez de la tarde. • 17:30 1 2 h 15 min 1 30 min 5 5 20:15 Hasta las 23:15 pasaron 3 horas. 11 • 1 siglo 5 100 años 100 2 80 5 20 Faltan 20 años. • 80 : 10 5 8 Tiene 8 décadas. 12 • 8:30 1 3 h 30 min 5 12:00 Termina a las 12 del mediodía. • Comenzó Terminó • Salida: 16:15 Regreso: 19:45 La visita a la cueva dura 3 horas y 30 minutos. Demuestra tu talento 13 2 € 5 200 céntimos 1 céntimo 200 monedas 2 céntimos 100 monedas 5 céntimos 40 monedas 10 céntimos 20 monedas 20 céntimos 10 monedas 50 céntimos 4 monedas Como le han dado más de 20 monedas y menos de 100, ha cambiado los 2 € por monedas de 5 céntimos y le han dado 40 monedas. Notas Competencias •  Competencia social y cívica. Plantee un debate en clase en el que aborde distintos temas relacionados con esta competencia y con el contexto que aparece en la actividad 12. Puede tratar asuntos como la importancia del deporte, el aprovechamiento sano del tiempo libre, el respeto a la naturaleza, la necesidad de la puntualidad en actividades sociales con otras personas… Pida a los alumnos que aporten sus ideas y opiniones. 8:30 15:45 12:00 16:30 Inteligencia naturalista 71
  • 72.
    Programar horarios Lorena trabajaen un gimnasio y prepara los horarios de las nuevas actividades propuestas para este año. 1 Fíjate en el horario del gimnasio y representa cada hora en un reloj de agujas. 2 Busca y representa en un reloj de agujas. La hora que hay pilates los lunes. La hora que hay aeróbic los miércoles. La hora de natación de los jueves. La hora de yoga del sábado. 3 Lee y contesta. Javier ha ido a apuntarse a natación y estas son las ofertas que le han ofrecido. Averigua cuál es la mejor opción si quiere ir: 40 días 60 días 3 meses 4 TRABAJO COOPERATIVO. Programa con tu compañero. Realizad un horario para el lunes por la tarde. Inventad las actividades que habría y la hora de comienzo y de finalización de cada una. SABER HACER EJEMPLO DE LUNES A VIERNES: Abierto de a 12 1 2 3 4 567 8 9 10 11 12 1 2 3 4 567 8 9 10 11 Abono mensual 48 € Abono trimestral 120 € Sesión de 1 día 1 € LUNES MIÉRCOLES VIERNES 8:10 Pilates Bicicleta Yoga 10:15 Bicicleta Aeróbic Pilates MARTES JUEVES SÁBADO 17:45 Pilates Bicicleta Yoga 19:50 Bicicleta Natación Pilates Gimnasio Salud HORARIO DE APERTURA LUNES A VIERNES: de 8:00 a 22:30. SÁBADOS: de 9:15 a 21:45. DOMINGOS: de 8:10 a 15:00. 140 ES0000000024590 663006-Unidad 09_22592.indd 140 10/03/2015 13:23:18 Propósitos •  Desarrollar la competencia matemática resolviendo problemas reales. •  Repasar contenidos básicos. Actividades pág. 140 1   De lunes a viernes: De                      a Sábado: De                      a Domingo: De                      a 2 •  Pilates •  Aeróbic •  Natación •  Yoga 3 •  40 días: sesión 1 día F 40 € •  60 días: sesión 1 día F 60 € •  3 meses: sesión 1 día F 90 € 4 R. L. Actividades pág. 141 1 •  Trescientos seis mil ochocientos noventa. •  Setecientos ochenta mil setenta y tres. •  Novecientos veinticinco mil trescientos seis. •  Dos millones novecientos ochenta mil noventa. •  Seis millones setenta y seis mil trescientos seis. •  Nueve millones doscientos ocho mil treinta y siete. Desarrollo de la competencia matemática •  En esta página, los alumnos aplican lo aprendido en la unidad   para resolver una situación real de horarios de diversas actividades   de un gimnasio. De esta manera, potencian su competencia matemática.  A la hora de plantear el trabajo cooperativo, pida a los alumnos que sean creativos a la hora de plantear y exponer los horarios de las actividades.   Puede pedirles también que varíen los precios de los abonos mensual  y trimestral de la actividad 3 y que averigüen para qué períodos de tiempo sería mejor cada uno. 12 1 2 3 4 567 8 9 10 11 12 1 2 3 4 567 8 9 10 11 12 1 2 3 4 567 8 9 10 11 12 1 2 3 4 567 8 9 10 11 12 1 2 3 4 567 8 9 10 11 12 1 2 3 4 567 8 9 10 11 12 1 2 3 4 567 8 9 10 11 12 1 2 3 4 567 8 9 10 11 12 1 2 3 4 567 8 9 10 11 12 1 2 3 4 567 8 9 10 11 12 1 2 3 4 567 8 9 10 11 12 1 2 3 4 567 8 9 10 11 12 1 2 3 4 567 8 9 10 11 12 1 2 3 4 567 8 9 10 11 12 1 2 3 4 567 8 9 10 11 12 1 2 3 4 567 8 9 10 11 12 1 2 3 4 567 8 9 10 11 12 1 2 3 4 567 8 9 10 11 12 1 2 3 4 567 8 9 10 11 12 1 2 3 4 567 8 9 10 11 12 1 2 3 4 567 8 9 10 11 12 1 2 3 4 567 8 9 10 11 12 1 2 3 4 567 8 9 10 11 12 1 2 3 4 567 8 9 10 11 12 1 2 3 4 567 8 9 10 11 12 1 2 3 4 567 8 9 10 11 12 1 2 3 4 567 8 9 10 11 12 1 2 3 4 567 8 9 10 11 12 1 2 3 4 567 8 9 10 11 12 1 2 3 4 567 8 9 10 11 12 1 2 3 4 567 8 9 10 11 12 1 2 3 4 567 8 9 10 11 12 1 2 3 4 567 8 9 10 11 12 1 2 3 4 567 8 9 10 11 12 1 2 3 4 567 8 9 10 11 12 1 2 3 4 567 8 9 10 11 12 1 2 3 4 567 8 9 10 11 12 1 2 3 4 567 8 9 10 11 12 1 2 3 4 567 8 9 10 11 12 1 2 3 4 567 8 9 10 11 12 1 2 3 4 567 8 9 10 11 12 1 2 3 4 567 8 9 10 11 12 1 2 3 4 567 8 9 10 11 12 1 2 3 4 567 8 9 10 11 12 1 2 3 4 567 8 9 10 11 12 1 2 3 4 567 8 9 10 11 12 1 2 3 4 567 8 9 10 11 12 1 2 3 4 567 8 9 10 11 12 1 2 3 4 567 8 9 10 11 12 1 2 3 4 567 8 9 10 11 12 1 2 3 4 567 8 9 10 11 12 1 2 3 4 567 8 9 10 11 12 1 2 3 4 567 8 9 10 11 12 1 2 3 4 567 8 9 10 11 12 1 2 3 4 567 8 9 10 11 12 1 2 3 4 567 8 9 10 11 12 1 2 3 4 567 8 9 10 11 12 1 2 3 4 567 8 9 10 11 12 1 2 3 4 567 8 9 10 11 12 1 2 3 4 567 8 9 10 11 12 1 2 3 4 567 8 9 10 11 12 1 2 3 4 567 8 9 10 11 12 1 2 3 4 567 8 9 10 11 12 1 2 3 4 567 8 9 10 11 12 1 2 3 4 567 8 9 10 11 12 1 2 3 4 567 8 9 10 11 12 1 2 3 4 567 8 9 10 11 12 1 2 3 4 567 8 9 10 11 12 1 2 3 4 567 8 9 10 11 12 1 2 3 4 567 8 9 10 11 12 1 2 3 4 567 8 9 10 11 12 1 2 3 4 567 8 9 10 11 12 1 2 3 4 567 8 9 10 11 12 1 2 3 4 567 8 9 10 11 12 1 2 3 4 567 8 9 10 11 12 1 2 3 4 567 8 9 10 11 12 1 2 3 4 567 8 9 10 11 12 1 2 3 4 567 8 9 10 11 12 1 2 3 4 567 8 9 10 11 12 1 2 3 4 567 8 9 10 11 12 1 2 3 4 567 8 9 10 11 12 1 2 3 4 567 8 9 10 11 12 1 2 3 4 567 8 9 10 11 12 1 2 3 4 567 8 9 10 11 12 1 2 3 4 567 8 9 10 11 12 1 2 3 4 567 8 9 10 11 12 1 2 3 4 567 8 9 10 11 12 1 2 3 4 567 8 9 10 11 12 1 2 3 4 567 8 9 10 11 12 1 2 3 4 567 8 9 10 11 12 1 2 3 4 567 8 9 10 11 12 1 2 3 4 567 8 9 10 11 12 1 2 3 4 567 8 9 10 11 12 1 2 3 4 567 8 9 10 11 12 1 2 3 4 567 8 9 10 11 12 1 2 3 4 567 8 9 10 11 12 1 2 3 4 567 8 9 10 11 12 1 2 3 4 567 8 9 10 11 12 1 2 3 4 567 8 9 10 11 12 1 2 3 4 567 8 9 10 11 72
  • 73.
    4 Escribe cómose lee cada fracción y contesta. 2 3 3 5 6 8 7 9 ¿Qué fracción tiene el numerador mayor? ¿Qué fracción tiene el denominador menor? 5 Copia y rodea en cada caso la fracción que se indica. La fracción mayor 1 5 y 2 5 3 7 y 2 7 7 9 y 4 9 La fracción menor 3 7 y 3 5 6 8 y 6 9 7 10 y 7 9 1 Escribe cómo se lee cada número. 306.890 2.980.090 780.073 6.076.306 925.306 9.208.037 2 Calcula el cociente y el resto de estas divisiones y haz la prueba. 149 ; 7 8.023 ; 27 492 ; 27 24.528 ; 24 6.242 ; 15 75.852 ; 34 3 Calcula. 8 1 7 2 9 2 3 (9 2 3) 2 2 1 4 9 2 5 1 8 2 2 12 2 (6 – 4) 1 7 6 3 4 2 3 2 5 (4 1 2) 3 2 2 5 10 2 2 3 3 1 9 3 3 (11 2 7) 2 8 6 Para el comedor del colegio, han traído 75 yogures de fresa, 65 de limón y 32 naturales. Hoy se han comido 20 de fresa, 15 de limón y 9 naturales. ¿Cuántos yogures han quedado? 7 Guillermo va a poner baldosas en una habitación y calcula que necesita un total de 180 baldosas. Guillermo ha comprado 3 cajas con 75 baldosas cada una. ¿Le sobran o le faltan baldosas? ¿Cuántas? 8 Enrique salió de casa con 120 €. Se gastó un tercio del dinero en la pescadería y 35 € en la frutería. ¿Cuánto dinero le quedó? 9 En un colegio hay 450 alumnos. Un quinto de los alumnos van a actividades extraescolares. ¿Cuántos alumnos no van a actividades extraescolares? 10 Patricia trabaja en un supermercado. Hoy tiene que colocar 48 zumos de naranja y 72 de limón en partes iguales entre 4 estanterías. ¿Cuántos zumos pondrá en cada una? 11 Juan ha comprado 4 camisetas iguales y un jersey por un total de 70 €. Si cada camiseta le ha costado 12 €, ¿cuánto le ha costado el jersey? 12 En un jardín hay 40 rosales. Un quinto es de rosas rojas, un cuarto de rosas blancas y el resto de rosas amarillas. ¿Cuántos rosales con rosas amarillas hay en el jardín? Problemas REPASO ACUMULATIVO 9 141 ES0000000024590 663006-Unidad 09_22592.indd 141 10/03/2015 13:23:19 UNIDAD 9 2 •  c 5 21, r 5 2 •  c 5 18, r 5 6 •  c 5 416, r 5 2 •  c 5 297, r 5 4 •  c 5 1.022 •  c 5 2.230, r 5 32 3 • 15 2 9 2 3 5 3 • 4 1 8 2 2 5 10 • 24 2 3 2 5 5 16 • 10 2 6 1 9 5 13 • 6 2 2 1 4 5 8 • 12 2 2 1 7 5 17 • 6 3 2 2 5 5 7 • 3 3 4 2 8 5 4 4 • Dos tercios •  Seis octavos •  Tres quintos •  Siete novenos •  La fracción 7 9 . • La fracción 2 3 . 5 •  2 5        •  3 7        •  7 9 •  3 7        •  6 9        •  7 10 6 (75 1 65 1 32) 2 2 (20 1 15 1 9) 5 128 Han quedado 128 yogures. 7 75 3 3 5 225 225 2 180 5 45 Le sobran 45 baldosas. 8 1/3 de 120 5 40 120 2 (40 1 35) 5 45 € Le quedaron 45 €. 9 1/5 de 450 5 90 450 2 90 5 360 No van 360 alumnos. 10 (48 1 72) : 4 5 30 En cada una pondrá 30 zumos. 11 70 2 4 3 12 5 22 El jersey le ha costado 22 €. 12  1 5 de 40 5 8 1 4 de 40 5 10 40 2 (8 1 10) 5 22 Hay 22 rosales amarillos. Repaso en común • Pida a los alumnos que realicen esta página de actividades de repaso y que anoten en sus cuadernos las actividades en las que han tenido alguna dificultad. Haga una puesta en común y para cada una de ellas pida a un alumno que salga a la pizarra y explique a sus compañeros cómo debería realizarse. La clase analizará su respuesta. Aproveche para concienciar a los alumnos de la importancia del repaso y de reflexionar sobre su aprendizaje. 73
  • 74.
    Longitud10 Contenidos de launidad SABER MEDIDA • El metro, el decímetro y el centímetro. • El milímetro. • El kilómetro, el hectómetro y el decámetro. SABER HACER MEDIDA • Reconocimiento del metro como unidad principal de longitud. • Identificación de los submúltiplos del metro y utilización de sus equivalencias con él y entre ellos. • Identificación de los múltiplos del metro y utilización de sus equivalencias con él y entre ellos. • Paso de medidas de forma compleja a incompleja y viceversa. • Ordenación de grupos de medidas. • Resolución de problemas reales donde aparezcan medidas de longitud. RESOLUCIÓN DE PROBLEMAS • Elección de la pregunta que hace que un problema se resuelva con dos operaciones. • Invención de un problema que se resuelva con unos cálculos dados y tenga una solución dada.   TAREA FINAL • Interpretar datos de altitudes. SABER SER FORMACIÓN EN VALORES • Valoración de la utilidad de las unidades de longitud. • Interés por la resolución de problemas reales. 74
  • 75.
    BIBLIOTECA DEL PROFESORADO Programacióndidáctica de aula Recursos para la evaluación • Evaluación de contenidos. Unidad 10: pruebas de control B y A. • Evaluación trimestral. Pruebas B, A y E. • Evaluación por competencias. Prueba 10. •  Rúbrica. Unidad 10. Enseñanza individualizada • Plan de mejora. Unidad 10. • Programa de ampliación. Unidad 10. Proyectos de trabajo cooperativo • Proyecto del segundo trimestre. Recursos complementarios • Fichas para el desarrollo de la inteligencia. • Operaciones y problemas. Aprendizaje eficaz • Técnicas de estudio y presentación de exámenes. Proyectos interdisciplinares • Programa de Educación en valores. • Programa de Educación emocional. • Inteligencias múltiples. RECURSOS DIGITALES LibroMedia • Unidad 10: actividades y recursos. MATERIAL DE AULA Láminas OTROS MATERIALES DEL PROYECTO Cuaderno del alumno • Segundo trimestre. Unidad 10. Solución de problemas. Método DECA SUGERENCIA DE TEMPORALIZACIÓN Enero MarzoFebrero La temporalización de esta unidad y de las siguientes puede variar en función de las fechas de la Semana Santa. ES0000000024590 663006_Matematicas_4_GRAZ_24259 PRIMARIA PRIMARIA Matemáticas PRIMARIA ANDALUCÍAMatemáticas ANDALUCÍA Matemáticas ANDALUCÍA ES0000 000024 590 663006 _Matem aticas_4_GRA Z_2425 9.indd 1 04/03/2 015 11:21:19 ES0000000024593 663039_Cdno_Matematicas_4-2_22732 PRIMARIA Matemáticas Segundo trimestre Matemáticas Segundo trimestre PRIMARIA CUADERNO CUADERNO ES0000000024593 663039_Cdno_Matematicas_4-2_22732.indd 1 19/02/2015 16:56:18 75
  • 76.
    10 Longitud Escalando montañas AIgnacio y a sus amigos les encanta escalar montañas. Hoy quieren ascender a la cima de una montaña cuya altura sea mayor de las que han escalado hasta ahora. Consultan el plano y entre todos eligen el pico Altomar. Ya están preparados para comenzar el camino y esperan batir su propio récord. ¡Buena escalada y buena suerte! Peñalón 2.490 m Altomar 3.120 m Montelado 4.390 m 142 ES0000000024590 663006-Unidad 10_22593.indd 142 10/03/2015 13:21:21 Peñalón 2.490 m Altomar 3.120 m Montelado 4.390 m Propósitos •  Reconocer situaciones de la vida real en las que se utilicen unidades de longitud. •  Recordar los conceptos básicos necesarios para el desarrollo   de la unidad. Previsión de dificultades •  Algunos alumnos pueden tener dificultad al pasar de unas unidades de longitud a otras. Recuerde cómo se multiplica y se divide por la unidad seguida de ceros. Puede ayudarles el escribir en fila todas las unidades que se vayan a trabajar, ordenadas de mayor a menor y,   si es necesario, indicar con flechas las relaciones entre ellas. •  Al establecer comparaciones   y realizar cálculos con medidas expresadas en distintas unidades, recuerde y razone con los alumnos que, para poder operar,   es necesario que las unidades   de medida sean las mismas. Trabajo colectivo sobre la lámina Haga que un alumno lea la lectura inicial y pídales que observen   en la lámina las montañas que hay representadas y digan cuál es su altura. Pregúnteles qué unidad de longitud se representa con la letra m y qué otras unidades de longitud conocen. 1 Montelado: cuatro mil trescientos noventa.  Altomar: tres mil ciento veinte. Peñalón: dos mil cuatrocientos noventa. 2 2.490 3.120 4.390 3 4.390 – 2.490 = 1.900  Es 1.900 m más alta. 4 1 km = 1.000 m    4 km = 4.000 m  Montelado tiene una altura  mayor que 4 km. 5 Si eligen escalar Altomar   es porque todas las que   han escalado hasta ahora tienen una altura inferior a 3.120 m. Otras formas de empezar •  Comente que en esta unidad vamos a medir longitudes: el largo, ancho   o alto de un objeto, la distancia entre dos objetos o lugares… Recuerde   que podemos utilizar distintos tipos de unidades, y pida a los alumnos que digan ejemplos de unidades de medida de cada tipo y que expliquen   con un ejemplo cómo se mide utilizando dicha unidad: –  Naturales (partes del cuerpo): palmos, pies, pasos… –  Arbitrarias (objetos elegidos por el grupo): un rotulador, un clip… –  Convencionales (iguales para todos): metro, centímetro, kilómetro… Señale las ventajas e inconvenientes de cada tipo de unidad (si todos obtenemos o no los mismos resultados, si necesitamos o no un instrumento para medir…). 76
  • 77.
    1 ¿Cuál esla altura de cada montaña? Escribe cómo se lee. 2 Ordena la altura de las montañas de menor a mayor. 3 ¿Cuántos metros es más alta Montelado que Peñalón? 4 ¿A cuántos metros equivale 1 kilómetro? ¿Qué pico del dibujo tiene una altura mayor de 4 kilómetros? 5 EXPRESIÓN ORAL. Explica esta afirmación: Ignacio y sus amigos solo han escalado montañas con una altura inferior a 2.490 m. Lee, comprende y razona ¿Qué sabes ya? TAREA FINAL Interpretar datos de altitudes Al final de la unidad analizarás datos de altitudes de ciudades. Antes, estudiarás las unidades de longitud. SABER HACER El metro, el decímetro, el centímetro y el kilómetro El metro (m) es la unidad principal de longitud. Para medir longitudes pequeñas, usamos unidades menores que el metro: el decímetro (dm) y el centímetro (cm). Para medir distancias o longitudes grandes, usamos una unidad mayor que el metro: el kilómetro (km). Las equivalencias entre estas unidades son: 1 metro 5 10 decímetros 1 m 5 10 dm 1 metro 5 100 centímetros 1 m 5 100 cm 1 kilómetro 5 1.000 metros 1 km 5 1.000 m 1 Calcula y completa en tu cuaderno. ¿Cuántos decímetros son? 2 m 8 m 14 m ¿Cuántos centímetros son? 3 m 5 m 27 m ¿Cuántos metros son? 4 km 9 km 12 km 2 Utiliza la regla y traza en tu cuaderno. Un segmento de 6 cm. Un segmento de 1 dm. 143 ES0000000024590 663006-Unidad 10_22593.indd 143 10/03/2015 13:21:23 UNIDAD 10 ¿Qué sabes ya? Recuerde a los alumnos las equivalencias del metro con el decímetro, centímetro y kilómetro. Después, pídales que realicen las actividades de forma individual y corríjalas en común despejando las dudas que hayan podido surgir. 1 • 20 dm 80 dm 140 dm •  300 cm 500 cm 2.700 cm • 4.000 m 9.000 m 12.000 m 2 R. L. Notas Competencias •  Comunicación lingüística. Es importante que los alumnos conozcan y utilicen los términos matemáticos correctamente. Al realizar la actividad de Expresión oral, anímelos a razonar de forma clara sus ideas usando vocabulario relacionado con la longitud. •  Aprender a aprender. Comente con los alumnos la importancia que tiene el afianzar los conceptos aprendidos para poder avanzar con seguridad. Señale que en esta unidad van a seguir aprendiendo sobre la longitud y conocerán nuevas unidades de medida. Inteligencia lingüística 77
  • 78.
    El metro, eldecímetro y el centímetro 1 Expresa en la unidad que se indica y completa en tu cuaderno. En decímetros 1 m y 5 dm 5 m y 4 dm 2 m y 7 dm 7 m y 8 dm 3 m y 8 dm 9 m y 3 dm En centímetros 1 m y 15 cm 6 m y 7 cm 4 m y 40 cm 8 m y 8 cm 5 m y 72 cm 9 m y 9 cm 2 ¿Cuántos centímetros mide cada cuerda? Calcula y completa. 4 m, 8 dm y 5 cm 6 m, 7 dm y 2 cm 9 m, 8 dm y 5 cm El metro es la principal unidad de longitud. El decímetro y el centímetro son unidades de longitud menores que el metro. La cinta roja mide 1 centímetro de ancho y 1 decímetro de largo. 1 decímetro 5 10 centímetros 1 dm 5 10 cm El paraguas que tiene Miguel mide 1 metro. 1 metro 5 10 decímetros 5 100 centímetros 1 m 5 10 dm 5 100 cm m dm cm 1 0 m dm cm 1 0 0 El decímetro y el centímetro son unidades de longitud menores que el metro. 1 dm 5 10 cm 1 m 5 10 dm 5 100 cm EJEMPLO 1 m y 5 dm 5 10 dm 1 5 dm 5 … dm EJEMPLO 1 m y 15 cm 5 100 cm 1 15 cm 5 … cm 144 ES0000000024590 663006-Unidad 10_22593.indd 144 10/03/2015 13:21:24 Propósitos •  Conocer y utilizar las equivalencias entre el metro, decímetro   y centímetro. •  Resolver problemas con medidas de longitud. Sugerencias didácticas Para explicar. Exprese que el metro es la principal unidad de longitud   y que en muchas situaciones reales necesitamos unidades menores que él, como el decímetro y el centímetro. Escriba en la pizarra las equivalencias entre ellas y realice algún ejemplo sencillo de paso de unas a otras. Comente que cuando se trata de pasar una medida en forma compleja a incompleja hay que pasar todas   las medidas a la unidad que se desea y sumarlas. Actividades 1 •  15 dm •  54 dm •  27 dm •  78 dm •  38 dm •  93 dm •  115 cm •  607 cm •  440 cm •  808 cm •  572 cm •  909 cm 2 Azul: 485 cm.    Roja: 672 cm.  Verde: 985 cm. 3 •  2 dm •  3 dm •  6 dm •  41 dm •  70 dm •  90 dm •  3 m •  4 m •  5 m •  72 m •  81 m •  90 m •  2 m •  5 m •  8 m •  45 m •  60 m •  700 m 4 •  19 cm 5 10 cm 1 9 cm 5   5 1 dm 1 9 cm •  45 cm 5 40 cm 1 5 cm 5 5 4 dm 1 5 cm •  86 cm 5 80 cm 1 6 cm 5 5 8 dm 1 6 cm •  356 cm 5 300 1 50 + 6 5 5 3 m 1 5 dm + 6 cm •  745 cm 5 700 1 40 + 5 5 5 7 m 1 4 dm + 5 cm •  680 cm 5 600 cm 1 80 cm 5 5 6 m 1 8 dm Otras actividades •  Coloque una cinta métrica en vertical en la pared de la clase, pegada   con celo, de manera que el «cero» coincida con el suelo. Agrupe   a los alumnos por parejas y pídales que, por turnos, salgan a medirse   unos a otros. En cada caso, el niño «medidor» dirá el número que aparece   en la cinta (medida en centímetros), otro compañero lo escribirá en la pizarra y, en común, se expresará dicha medida en metros y centímetros, y en metros, decímetros y centímetros. Por ejemplo: Dirán: «Andrés mide 137 centímetros». Escribirán: 137 cm 5 1 m y 37 cm 5 1 m, 3 dm y 7 cm. 78
  • 79.
    10 3 Expresa enla unidad indicada. En decímetros 20 cm 410 cm 30 cm 700 cm 60 cm 900 cm En metros 30 dm 720 dm 40 dm 810 dm 50 dm 900 dm En metros 200 cm 4.500 cm 500 cm 6.000 cm 800 cm 7.000 dm 4 Lee y completa en tu cuaderno. HAZLO ASÍ 43 cm 5 40 cm 1 3 cm 5 5 4 dm 1 3 cm 19 cm 5 … dm 1 … cm 45 cm 5 … dm 1 … cm 86 cm 5 … dm 1 … cm HAZLO ASÍ 257 cm 5 200 cm 1 50 cm 1 7 cm 5 5 2 m 1 5 dm 1 7 cm 356 cm 5 … m 1 … dm 1 … cm 745 cm 5 … m 1 … dm 1 … cm 680 cm 5 … m 1 … dm Problemas 5 Resuelve. Gabriel tiene una cometa roja y otra cometa verde. La cuerda de la cometa roja mide 8 m, 6 dm y 9 cm, y la cuerda de la cometa verde mide 7 m, 3 dm y 5 cm. ¿Cuántos centímetros mide la cuerda verde menos que la roja? ¿Cuántos centímetros le faltan a la cuerda roja para medir 9 m? Suma números de dos cifras sin llevar descomponiendo los sumandos 31 1 23 28 1 61 43 1 26 42 1 51 41 1 37 51 1 38 54 1 43 56 1 42 67 1 12 76 1 22 83 1 16 94 1 15 CÁLCULO MENTAL EJEMPLO 20 cm 5 2 dm : 10 EJEMPLO 30 dm 5 3 m : 10 EJEMPLO 200 cm 5 2 m : 100 24 1 52 5 70 1 6 5 76 145 ES0000000024590 663006-Unidad 10_22593.indd 145 10/03/2015 13:21:25 UNIDAD 10 5   •  Roja: 869 cm. Verde: 735 cm. 869 2 735 5 134 La cuerda verde mide 134 cm menos que la roja. •  9 m 5 900 cm 900 2 869 5 31 Para medir 9 m a la cuerda roja le faltan 31 cm. Cálculo mental •  54 •  89 •  69 •  93 •  78 •  89 •  97 •  98 •  79 •  98 •  99 •  109 Notas Otras actividades •  Nombre en común ejemplos de longitudes de objetos que podamos medir en metros, en decímetros y en centímetros. Después, pida a los alumnos que midan algunos objetos que se encuentren en la clase: el largo de un lapicero, el ancho de la mesa, el largo de la pizarra…, utilizando la regla para medir en centímetros y la cinta métrica para hacerlo en metros. Anímelos a estimar la medida antes de realizar la medición. Al final, haga una puesta en común, escriba en la pizarra las medidas obtenidas y exprese, de forma colectiva, dichas medidas en varias unidades, trabajando las equivalencias presentadas en esta doble página. 79
  • 80.
    En metrosEn centímetros Elmilímetro 1 Expresa en milímetros y completa en tu cuaderno. 3 cm 7 cm 12 cm 48 cm 2 m 5 m 32 m 58 m 5 cm y 8 mm 9 cm y 4 mm 5 m y 7 mm 6 m y 3 mm 2 Expresa en la unidad que se indica. 30 mm 120 mm 500 mm 80 mm 430 mm 800 mm 4.000 mm 84.000 mm 7.000 mm 92.000 mm El milímetro es una unidad de longitud menor que el centímetro. El milímetro lo usamos para medir longitudes muy pequeñas. El clip mide 7 milímetros de ancho y 3 centímetros y 2 milímetros de largo. 1 centímetro 5 10 milímetros 1 cm 5 10 mm 1 metro 5 1.000 milímetros 1 m 5 1.000 mm m dm cm mm 1 0 m dm cm mm 1 0 0 0 El milímetro es una unidad de longitud menor que el centímetro. 1 cm 5 10 mm 1 m 5 1.000 mm RECUERDA 1 cm 5 10 mm 1 m 5 1.000 mm EJEMPLO 30 mm 5 3 cm : 10 EJEMPLO 4.000 mm 5 4 m : 1.000 146 ES0000000024590 663006-Unidad 10_22593.indd 146 10/03/2015 13:21:26 Propósitos •  Reconocer el milímetro como   una unidad de longitud menor   que el centímetro •  Utilizar las equivalencias entre centímetro y metro con el milímetro. Sugerencias didácticas Para explicar. Lea la situación inicial y comente que a veces es necesario utilizar una unidad más pequeña   que el centímetro: el milímetro. Escriba su nombre y abreviatura en la pizarra. Pida a los alumnos que observen   la regla e indíqueles la señalización de los centímetros y milímetros y pídales que cuenten cuántos milímetros tiene un centímetro. Escriba en la pizarra   las equivalencias del centímetro   y el metro con el milímetro. Para reforzar. Pida a los alumnos que preparen un cuadro en el que aparezcan el metro y sus submúltiplos y las equivalencias que han trabajado. Anímelos a ser creativos. Actividades 1   •  30 mm •  2.000 mm •  70 mm •  5.000 mm •  120 mm •  32.000 mm •  480 mm •  58.000 mm •  58 mm •  94 mm •  5.007 mm •  6.003 mm 2   •  3 cm •  12 cm •  50 cm •  8 cm •  43 cm •  80 cm •  4 m •  84 m •  7 m •  92 m 3   •  19 mm 5 10 mm 1 9 mm 5   5 1 cm 1 9 mm •  28 mm 5 20 mm 1 8 mm 5  5 2 cm 1 8 mm •  45 mm 5 40 mm 1 5 mm 5  5 4 cm 1 5 mm 4 •  37 mm , 39 mm , 40 mm •  56 mm , 60 mm , 540 mm •  85 mm , 90 mm , 750 mm Otras actividades •  Forme grupos de 4 o 5 alumnos y entregue a cada grupo un folio para   que cada alumno trace libremente, con un rotulador de distinto color,   una línea recta utilizando una regla. A continuación, indíqueles que comparen las líneas dibujadas y que estimen cuál es la más larga y la más corta, cuáles miden menos y más de 1 decímetro… Por último, indíqueles que midan   con la regla la longitud de cada línea y den el resultado, primero, en milímetros y, después, en centímetros y milímetros. 80
  • 81.
    MARIQUITA 7 mm SALTAMONTES 3 cmy 5 mm HORMIGA 5 mm GUSANO 7 cm y 9 mm 10 Lee y contesta. Javier ha sumado dos de estas longitudes y ha obtenido como resultado 4 cm. ¿Qué dos longitudes ha sumado Javier? RAZONAMIENTO 3 Completa en tu cuaderno. 19 mm 5 … cm 1 … mm 28 mm 5 … cm 1 … mm 45 mm 5 … cm 1 … mm 4 Expresa en milímetros y ordena las longitudes de cada grupo de menor a mayor. Problemas 5 Lee y resuelve. Daniela está leyendo un artículo sobre la longitud de algunos animales. ¿Cuántos milímetros en total miden una mariquita y una hormiga? ¿Cuántos centímetros y milímetros son? ¿Cuántos milímetros mide un saltamontes? ¿Cuántos milímetros mide un saltamontes más que una mariquita? ¿Cuántos milímetros mide un gusano de seda más que un saltamontes? HAZLO ASÍ 39 mm 4 cm 3 cm y 7 mm 5 cm y 6 mm 8 cm y 5 mm 6 cm 54 cm 9 cm 75 cm 2 cm y 5 mm 20 mm 15 mm 3 cm 75 mm 5 70 mm 1 5 mm 5 5 7 cm 1 5 mm 147 ES0000000024590 663006-Unidad 10_22593.indd 147 10/03/2015 13:21:28 Inteligencia naturalista UNIDAD 10 5 • 7 mm 1 5 mm 5 12 mm 5 5 1 cm 1 2 mm Miden 12 mm; 1 cm y 2 mm. • 30 mm 1 5 mm 5 35 mm Un saltamontes mide 35 mm. • 35 mm 2 7 mm 5 28 mm Un saltamontes mide 28 mm más que una mariquita. • 79 mm 2 35 mm 5 44 mm Un gusano de seda mide 44 mm más que un saltamontes. Razonamiento Expresamos todas las medidas en milímetros y calculamos. 25 mm   20 mm   15 mm   30 mm 4 cm 5 40 mm 5 25 mm 1 15 mm Javier ha sumado 2 cm y 5 mm y 15 mm. Notas Otras actividades • Fomente en los alumnos la estimación de longitudes de objetos cotidianos. Al principio, pueden tener a la vista una regla y una cinta métrica y quitar posteriormente dicho apoyo. Propóngales que estimen las siguientes longitudes en la unidad indicada, y después las midan para comprobar dicha estimación: –  En centímetros, el largo de un bolígrafo y el ancho de la mesa. – En milímetros, el grosor de un libro y el lado de un cuadradito del cuaderno. –  En metros, el ancho de la puerta y el largo de la clase. 81
  • 82.
    El kilómetro, elhectómetro y el decámetro 1 Expresa en metros y completa en tu cuaderno. 2 dam 14 dam 4 dam 25 dam 3 hm 15 hm 4 hm 37 hm 7 km 58 km 9 km 95 km 2 Expresa en metros. 3 dam y 5 m 7 dam y 8 m 12 dam y 7 m 34 dam y 9 m 4 hm y 16 m 6 hm y 25 m 15 hm y 6 m 29 hm y 8 m 6 km y 462 m 8 km y 175 m 17 km y 92 m 45 km y 5 m 3 Calcula y expresa en la unidad que se indica. En decámetros En hectómetros En kilómetros 20 m 80 m 50 m 90 m 400 m 700 m 600 m 800 m 3.000 m 6.000 m 4.000 m 8.000 m El kilómetro, el hectómetro y el decámetro son unidades de longitud mayores que el metro y se utilizan para medir distancias o longitudes muy grandes. Fíjate en las relaciones de estas unidades con el metro. 1 kilómetro 5 1.000 metros 1 km 5 1.000 m 1 hectómetro 5 100 metros 1 hm 5 100 m 1 decámetro 5 10 metros 1 dam 5 10 m km hm dam m 1 0 0 0 km hm dam m 1 0 0 km hm dam m 1 0 El kilómetro, el hectómetro y el decámetro son unidades de longitud mayores que el metro. 1 km 5 1.000 m 1 hm 5 100 m 1 dam 5 10 m RECUERDA 1 dam 5 10 m 1 hm 5 100 m 1 km 5 1.000 m EJEMPLO 20 m 5 2 dam : 10 EJEMPLO 400 m 5 4 hm : 100 EJEMPLO 3.000 m 5 3 km : 1.000 148 ES0000000024590 663006-Unidad 10_22593.indd 148 10/03/2015 13:21:29 Propósitos •  Reconocer el kilómetro, el hectómetro y el decámetro como unidades de longitud mayores   que el metro. •  Conocer y aplicar las equivalencias entre el metro y sus múltiplos. •  Resolver problemas con unidades de longitud. Sugerencias didácticas Para explicar. Comente con los alumnos que para medir longitudes grandes utilizamos unidades mayores que el metro. Escriba en la pizarra   las tres unidades y sus abreviaturas. Explique la equivalencia de cada  unidad con el metro y pida   a los alumnos que las memoricen. Para reforzar. Pida a los alumnos que preparen un cuadro en el que aparezcan el metro y sus múltiplos   y sus equivalencias. Actividades 1 •  20 m •  140 m •  40 m •  250 m •  300 m •  1.500 m •  400 m •  3.700 m •  7.000 m •  58.0000 m •  9.000 m •  95.000 m 2 •  35 m •  416 m •  78 m •  625 m •  127 m •  1.506 m •  349 m •  2.908 m •  6.462 m •  8.175 m •  17.092 m •  45.005 m 3 •  2 dam •  8 dam •  5 dam •  9 dam •  4 hm •  7 hm •  6 hm •  8 hm •  3 km •  6 km •  4 km •  8 km 4 •  56 m 5 5 dam 1 6 m •  64 m 5 6 dam 1 4 m •  72 m 5 7 dam 1 2 m •  89 m 5 8 dam 1 9 m Otras actividades •  Lleve a clase un mapa de carreteras y comente que en él están indicadas, en kilómetros, las distancias entre ciudades y pueblos. Haga una fotocopia de la zona del mapa donde se encuentre su localidad y repártala por grupos a los alumnos, para realizar ejercicios de interpretación: preguntándoles,   por ejemplo, qué distancia hay entre dos localidades concretas,   para que la expresen en kilómetros y en metros. •  Fotocopie y entregue a los alumnos una tabla de distancias entre   las capitales de provincia de España, explique con un ejemplo cómo  se maneja y busque en común la distancia entre dos ciudades  conocidas por los alumnos. 82
  • 83.
    4 Descompón cadamedida usando el mayor número de unidades posible. 56 m 72 m 64 m 89 m 278 m 698 m 583 m 810 m 1.367 m 5.309 m 2.876 m 7.012 m Problemas 5 Observa el plano y resuelve. ¿Cuántos metros mide cada camino? Paula va de la ciudad A a la ciudad B por el camino más corto y vuelve a la ciudad A por el más largo. ¿Cuántos metros recorre Paula en total? Ramiro vive en la ciudad B. Cada día va a la ciudad A por el camino verde y vuelve a la ciudad B por el mismo camino. ¿Cuántos metros recorre cada día? ¿Cuántos kilómetros y metros son? Cada día, un autobús sale de la ciudad A a la ciudad B por la ruta roja y para a la mitad del camino. ¿A cuántos kilómetros de la ciudad B tiene la parada? Inventa un camino de dos tramos de la ciudad A a la ciudad B cuya longitud sea de 2 km. 10 4 Descompón cada medida usando el mayor número de unidades posible. 56 m 72 m 64 m 89 m 278 m 698 m 583 m 810 m 1.367 m 5.309 m 2.876 m 7.012 m Problemas 5 Observa el plano y resuelve. ¿Cuántos metros mide cada camino? Paula va de la ciudad A a la ciudad B por el camino más corto y vuelve a la ciudad A por el más largo. ¿Cuántos metros recorre Paula en total? Ramiro vive en la ciudad B. Cada día va a la ciudad A por el camino verde y vuelve a la ciudad B por el mismo camino. ¿Cuántos metros recorre cada día? ¿Cuántos kilómetros y metros son? Cada día, un autobús sale de la ciudad A a la ciudad B por la ruta roja y para a la mitad del camino. ¿A cuántos kilómetros de la ciudad B tiene la parada? Inventa un camino de dos tramos de la ciudad A a la ciudad B cuya longitud sea de 2 km. Suma números de dos cifras llevando descomponiendo los sumandos 32 1 28 23 1 47 47 1 13 45 1 35 41 1 39 51 1 39 56 1 14 54 1 16 62 1 18 69 1 21 68 1 22 74 1 26 CÁLCULO MENTAL HAZLO ASÍ 75 m 5 70 m 1 5 m 5 7 dam 1 5 m 346 m 5 300 m 1 40 m 1 6 m 5 3 hm 1 4 dam 1 6 m 8.273 m 5 8.000 m 1 200 m 1 70 m 1 3 5 8 km 1 2 hm 1 7 dam 1 3 m 36 1 24 5 50 1 10 5 60 49 km 41km 25 hm 125m 39 km y725 m 40 km y 5 hm 36 km y 5 hm 37kmy12dam 32 km 20 km 75 dam A B 149 ES0000000024590 663006-Unidad 10_22593.indd 149 10/03/2015 13:21:34 UNIDAD 10 • 278 m 5 2 hm 1 7 dam 1 8 m • 583 m 5 5 hm 1 8 dam 1 3 m • 698 m 5 6 hm 1 9 dam 1 8 m • 810 m 5 8 hm 1 1 dam • 1.367 m 5 1 km 1 3 hm 1 1 6 dam 1 7 m • 2.876 m 5 2 km 1 8 hm 1 1 7 dam 1 6 m • 5.309 m 5 5 km 1 3 hm 1 9 m • 7.012 m 5 7 km 1 1 dam 1 2 m 5 • Verde: 39.725 m 1 36.500 m 1 1 20.000 m 1 750 m 5 5 96.975 m Rojo: 41.000 m 1 2.500 m 1 1 125 m 5 43.625 m Azul: 40.500 m 1 49.000 m 1 1 32.000 m 1 37.120 m 5 5 158.620 m • 43.625 m 1 158.620 m 5 5 202.245 m 5 202 km y 245 m • 96.975 m 3 2 5 193.950 m 5 5 193 km y 950 m • 43.625 : 2 c 5 21.812, r 5 1 21.812 m 5 21 km y 812 m El autobús tiene la parada a 21 km y 812 m de la ciudad B. • R. L. Cálculo mental •  60 •  70 •  60 •  80 •  80 •  90 •  70 •  70 •  80 •  90 •  90 •  100 Notas Competencias •  Conciencia y expresión cultural. La interpretación de croquis es un procedimiento muy importante que aúna las Matemáticas y los contenidos artísticos. Comente con los alumnos las características de los croquis, mostrando que son dibujos aproximados en los que recogemos distintas informaciones. Pídales que creen uno ellos mismos a partir de una descripción dada por usted y plantee después distintas actividades similares a las trabajadas. 83
  • 84.
    Elige la preguntapara que el problema se resuelva con dos operaciones y resuelve. 1 En las rebajas, Marina compró 3 chándales a 24 € cada uno y unas deportivas por 35 €. Preguntas A. ¿Cuánto le costaron las deportivas más que un chándal? B. ¿Cuánto le costaron en total los chándales? C. ¿Cuánto se gastó en total Marina? 2 Luis lleva en su furgoneta 100 cajas de refrescos. En el primer supermercado deja 15 cajas y el resto las reparte en partes iguales entre otros 5 supermercados. Preguntas A. ¿Cuántas cajas lleva después de salir del primer supermercado? B. ¿Cuántas cajas de refrescos deja en cada supermercado? C. ¿Cuántos refrescos reparte entre los 5 supermercados? Vamos a leer el problema y las preguntas dadas. Después, elegimos la pregunta para que el problema se resuelva con dos operaciones. A Raquel le han regalado un juego de construcción con 75 piezas rojas, 80 azules y 95 amarillas. Ha utilizado la mitad de las piezas para hacer un robot. Preguntas A. ¿Cuántas piezas tiene el juego en total? B. ¿Cuántas piezas amarillas más que rojas tiene el juego? C. ¿Cuántas piezas utilizó Raquel para hacer el robot? La pregunta que se responde con dos operaciones es la C. 1.º Calcula las piezas que tiene el juego en total. 75 1 80 1 95 5 250 2.º Calcula las piezas que utiliza para hacer el robot. 250 : 2 5 125 Solución: Raquel ha utilizado 125 piezas para hacer el robot. Elegir la pregunta para que el problema se resuelva con dos operaciones Solución de problemas 150 ES0000000024590 663006-Unidad 10_22593.indd 150 10/03/2015 13:21:40 Propósitos •  Elegir la pregunta para que un problema se resuelva con dos operaciones. •  Inventar problemas que se resuelvan con unos cálculos dados y que tengan una solución dada. Sugerencias didácticas Para explicar. Lea el problema   y las preguntas y explique   a los alumnos que debemos elegir   la pregunta para que el problema   se resuelva con dos operaciones.   Lea cada pregunta, pídales qué digan qué operación u operaciones hay que realizar para responderla y pregúnteles cuál es la pregunta correcta. Actividades 1 C. ¿Cuánto se gastó en total?   3 3 24 5 72  72 1 35 5 107  Marina se gastó 107 €. 2 B. ¿Cuántas cajas de refrescos deja en cada supermercado?  100 2 15 5 85  85 : 5 5 17  En cada supermercado deja   17 cajas. 3 R. M. ¿Cuántos kilos de tomates le quedaron?  12 3 6 5 72; 72 2 10 5 62  Le quedaron 62 kilos. 4 R. M. ¿Cuántas canciones   ha grabado en total?  32 3 4 5 128   128 1 19 5 147   Ha grabado 147 canciones. 5 R. M. ¿Cuántas monedas  le han dado en total?  100 1 50 5 150; 150 : 25 75  Le han dado 75 monedas. 6 R. M. ¿Cuántos metros medía cada trozo?  40 2 4 5 36; 36 : 9 5 4  Cada trozo medía 4 metros. 7 R. M. ¿Cuántas llamadas atendió el domingo Nuria?  124 1 72 5 196; 196 : 25 98  Atendió 98 llamadas. Otras actividades •  Presente a los alumnos algunos textos para que inventen problemas  de dos operaciones, utilizando algunos datos del texto. Corríjalos  al final de forma colectiva. Dícteles por ejemplo el siguiente texto y pídales que inventen un problema   de suma y resta, otro de suma y multiplicación y otro de suma y división: «Las tres clases de 4.º han organizado un viaje de 5 días para visitar  los principales monumentos de su comunidad. En total van 60 alumnos:   20 de 4.º A, 18 de 4.º B y el resto de 4.º C. El precio del viaje por persona es: 45 € el alojamiento y 40 € la comida, además de 50 € de transporte». 84
  • 85.
    Escribe un problemaque se resuelva con cada grupo de cálculos y tenga la solución dada. 1 3 10 Lee y escribe una pregunta para que el problema se resuelva con dos operaciones. Después, resuélvelo. 3 Lucía recogió en su huerto 12 cajas con 6 kilos de tomates cada una y regaló 10 kilos de tomates a su amiga. 4 Miguel ha grabado 4 CD de música, con 32 canciones cada uno, y 1 CD, con 19 canciones. 5 Gustavo necesita monedas de 2 € para su tienda. Ha ido al banco a cambiar un billete de 100 € y otro de 50 € por monedas de 2 €. 6 Para hacer disfraces, Susana compró 40 m de cinta. Primero cortó 4 m y el resto lo partió en 9 trozos iguales. 7 Nuria es recepcionista de un hotel. El sábado atendió 125 llamadas por la mañana y 72 por la tarde. El domingo atendió la mitad de llamadas que el sábado. 8 Para pagar una factura, Javier ha entregado 7 billetes de 50 € y un billete de 20 €. INVENTA TUS PROBLEMAS Escribe un problema que se resuelva con cada grupo de cálculos y tenga la solución dada. 1 3 12 1 23 1 35 5 70 70 3 15 5 1.050 Solución: Por los jerséis recibidos en su tienda, Ana pagó 1.050 €. 90 2 15 5 75 75 : 3 5 25 Solución: Cada cinturón le costó 25 €. 28 1 20 5 48 48 : 6 5 8 Solución: En cada frutero Pablo ha puesto 8 piezas de fruta. 2 Camiseta 15 € 151 ES0000000024590 663006-Unidad 10_22593.indd 151 10/03/2015 13:21:42 UNIDAD 10 8 R. M. ¿Cuál es el importe total de la factura? 7 3 50 5 350; 350 1 20 5 370 El importe total de la factura es de 370 €. Inventa tus problemas 1 R. M. Ana ha recibido en su tienda 12 jerséis rojos, 23 azules y 35 verdes. Cada jersey cuesta 15 €. ¿Cuánto ha pagado en total? 2 R. M. Pablo tenía 28 manzanas y 20 peras. Las ha repartido en partes iguales en 6 fruteros. ¿Cuántas piezas de fruta ha puesto en cada frutero? 3 R. M. Marta tenía 90 €. Compró una camiseta por 15 € y con el resto de su dinero compró 3 cinturones iguales. ¿Cuánto le costó cada cinturón? Notas Competencias •  Iniciativa y emprendimiento. El programa de invención de problemas es un contexto muy adecuado para el desarrollo de esta competencia. Anime a los alumnos a ser creativos a la hora de crear los problemas y de exponerlos a sus compañeros, sin abandonar por ello la corrección matemática. Valore sus logros y muéstreles cómo sus capacidades van aumentado con la práctica. 85
  • 86.
    6 Expresa enmetros. 2 dam y 6 m 5 hm y 4 m 4 dam y 3 m 2 km y 145 m 3 hm y 25 m 7 km y 90 m 7 Expresa en la unidad indicada. En dam: 40 m 80 m 190 m En hm: 300 m 700 m 1.500 m En km: 5.000 m 9.000 m 21.000 m 8 Expresa cada medida usando el mayor número de unidades posible. Fíjate en los ejemplos. 63 cm 89 cm 95 cm 163 cm 489 cm 720 cm 134 m 568 m 712 m 2.789 m 4.720 m 6.914 m 9 Observa el dibujo y ordena. De menor a mayor, la longitud de estos rollos de cinta. De mayor a menor, las distancias recorridas por estas motos. 1 VOCABULARIO. Escribe el nombre de las unidades que se indican. Tres unidades de longitud menores que el metro. Tres unidades de longitud mayores que el metro. 2 Copia y completa en tu cuaderno. 1 m 5 … dm 23 m 5 … mm 7 m 5 … cm 45 m 5 … mm 1 dm 5 … cm 14 dm 5 … cm 8 dm 5 … cm 31 m 5 … cm 1 cm 5 … mm 62 cm 5 … mm 9 cm 5 … mm 74 cm 5 … mm 3 Expresa en metros. 10 dm 300 cm 2.000 mm 40 dm 600 cm 5.000 mm 70 dm 800 cm 9.000 mm 4 Expresa en la unidad que se indica. 4 m, 5 dm y 7 cm 2 m, 6 dm y 9 cm 17 m, 8 dm y 9 cm 3 m, 8 cm y 5 mm 5 m, 4 cm y 6 mm 14 m, 9 cm y 7 mm 5 Ordena cada grupo de medidas de mayor a menor. 4.000 mm 41 dm 4 m y 9 cm 9 dm y 5 cm 960 cm 9.000 mm 3 m y 2 dm 330 cm 34 dm 7.000 mm 690 cm 68 dm ACTIVIDADES En centímetros En milímetros EJEMPLO 257 cm 5 200 cm 1 50 cm 1 7 cm 5 5 2 m 1 5 dm 1 7 cm 468 m 5 400 m 1 60 m 1 8 m 5 5 4 hm 1 6 dam 1 8 m 24 km y 15 hm 3 m y 80 dm 2 dam y 9 m 1 hm y 20 dam 76 km y 9 dam 58 km y 7 hm 152 ES0000000024590 663006-Unidad 10_22593.indd 152 10/03/2015 13:21:43 Propósitos •  Repasar los contenidos básicos   de la unidad. Actividades 1 •  Decímetro, centímetro   y milímetro. •  Decámetro, hectómetro   y kilómetro. 2 •  10 dm •  23.000 mm •  700 cm •  45.000 mm •  10 cm •  140 cm •  80 cm •  3.100 cm •  10 mm •  620 mm •  90 mm •  740 mm 3 •  1 m •  3 m •  2 m •  4 m •  6 m •  5 m •  7 m •  8 m •  9 m 4 •  457 cm •  269 cm •  1.789 cm •  3.085 mm •  5.046 mm •  14.097 mm 5 •  41 dm . 4 m y 9 cm . 4.000 mm •  960 cm . 9.000 mm .   . 9 dm y 5 cm •  34 dm . 330 cm . 3 m y 2 dm •  7.000 mm . 690 cm . 68 dm 6 •  26 m •  504 m •  43 m •  2.145 m •  325 m •  7.090 m 7 •  4 dam 8 dam 19 dam •  3 hm 7 hm 15 hm •  5 km 9 km 21 km 8 •  6 dm 1 3 cm •  8 dm 1 9 cm •  9 dm 1 5 cm •  1 m 1 6 dm 1 3 cm •  4 m 1 8 dm 1 9 cm •  7 m 1 2 dm •  1 hm 1 3 dam 1 4 m •  5 hm 1 6 dam 1 8 m •  7 hm 1 1 dam 1 2 m •  2 km 1 7 hm 1 8 dam 1 9 m •  4 km 1 7 hm 1 2 dam •  6 km 1 9 hm 1 1 dam 1 4 m Otras actividades •  Escriba en la pizarra un cuadro con las abreviaturas de las unidades  de longitud trabajadas, ordenadas de mayor a menor. Pregunte y escriba  en cada caso en las flechas de arriba qué operación hacemos  para pasar de una unidad a otra. Después, comente que cada unidad  es 10 veces la siguiente y complete el resto de las equivalencias. 3 10 3 10 3 10 3 10 3 10 3 10 km hm dam m dm cm mm 3 1.0003 1.000 3 1003 100 3 103 10 86
  • 87.
    12 Resuelve. Micaela mirael plano de los nuevos pisos que van a construir en su barrio. ¿Cuántos metros de largo mide la habitación A? ¿Cuántos centímetros son? ¿Cuántos metros de ancho mide la habitación B? ¿Y el baño? El salón tiene un rodapié de madera. ¿Cuántos metros de rodapié tiene si el ancho de la puerta es de 1 m y 90 cm? En la habitación B hay un armario empotrado en la pared que mide 6 m. El armario mide de ancho 1 m, 4 dm y 5 cm. ¿Cuántos centímetros de pared quedan libres? Problemas 10 Lee y resuelve. Virginia va a poner en la cocina un lavavajillas de 6 dm de ancho, un mueble de 6 dm y 8 cm de ancho y una lavadora de 65 cm de ancho. ¿Cuántos metros y centímetros ocuparán si los coloca todos unidos en fila? Pablo tiene un póster, de 3 dm y 5 cm de ancho y 1 m y 5 cm de alto, y le pone un listón de madera alrededor. ¿Cuántos centímetros de listón necesita? 11 Resuelve. La montaña más alta del mundo es el Everest, cuya altura es de 8.848 m, y la altura de la segunda montaña más alta es de 2 hm, 3 dam y 7 m menos. ¿Cuántos metros de altura tiene la segunda montaña más alta del mundo? 10 13 Miguel mide 1 m y 35 cm. Paula le dice a su hermano Miguel: «Si me subo a un taburete de 15 cm de altura y tú te agachas 1 dm, mido igual que tú». ¿Cuál es la altura de Paula? Demuestra tu talento Habitación B Habitación A Baño Salón Cocina 3 m 6 m 4 m 6 m 3m2m 2m 12 Resuelve. Micaela mira el plano de los nuevos pisos que van a construir en su barrio. ¿Cuántos metros de largo mide la habitación A? ¿Cuántos centímetros son? ¿Cuántos metros de ancho mide la habitación B? ¿Y el baño? El salón tiene un rodapié de madera. ¿Cuántos metros de rodapié tiene si el ancho de la puerta es de 1 m y 90 cm? En la habitación B hay un armario empotrado en la pared que mide 6 m. El armario mide de ancho 1 m, 4 dm y 5 cm. ¿Cuántos centímetros de pared quedan libres? 153 ES0000000024590 663006-Unidad 10_22593.indd 153 10/03/2015 13:21:46 UNIDAD 10 9 • 3 m y 80 dm , 2 dam y 9 m , , 1 hm y 20 dam • 76 km y 9 dam . . 58 km y 7 hm . . 24 km y 15 hm 10 • 60 cm 1 68 cm 1 65 cm 5 5 193 cm 5 1 m y 93 cm Ocupan 1 m y 93 cm. • 35 3 2 1 105 3 2 5 280 Necesita 280 cm de listón. 11  8.848 2 237 5 8.611 Mide 8.611 m. 12  • Habitación A: 4 m 5 400 cm. • Habitación B: 2 m. Baño: 2 m. • 2 3 6 1 2 3 3 2 1,9 5 16,1 Necesita 16,1 m de listón. • 600 2 145 5 455 Quedan libres 455 cm. Demuestra tu talento 13  Miguel mide 135 cm. 135 2 10 2 15 5 110 cm La altura de Paula es 110 cm. Notas Competencias •  Competencia social y cívica. La casa y lo que se refiere a ella es un contexto muy familiar y motivador para los alumnos. Suscite un debate sobre temas relacionados con la casa como el respeto por los demás, la colaboración en las tareas del hogar, la convivencia con los vecinos… Puede pedirles también que hagan un croquis parecido de sus casas y realicen actividades similares a las planteadas. Inteligencia espacial 87
  • 88.
    Interpretar datos dealtitudes Hoy en clase han hecho un esquema comparando altitudes de ciudades. En él aparece la ciudad de mayor altitud del mundo, La Rinconada, y la altitud a la que están algunas ciudades españolas. 1 Descompón la altitud de cada ciudad y exprésala usando todas las unidades de longitud posibles. Ávila Madrid Sevilla 2 Observa y resuelve. ¿Cuál es la altitud de Madrid menos que la de La Rinconada en metros? ¿Cuántos kilómetros y metros son? ¿Cuánto es la altitud de Madrid más que la de Sevilla en metros? ¿Cuántos hectómetros y metros son? Virginia vive en Ávila y va a Sevilla a visitar a una amiga. ¿Cuántos metros tiene que descender? ¿Cuántos kilómetros y metros son? Jaime vive en Madrid y hoy tiene que ir a Ávila. ¿Cuántos metros tiene que ascender? ¿Cuántos hectómetros y metros son? 3 TRABAJO COOPERATIVO. Buscad y plantead. Averigua con tu compañero la altitud de otras ciudades y plantead problemas similares a los propuestos en esta página. Después, resolvedlos. SABER HACER EJEMPLO La Rinconada: 5.099 m 5 … m 1 … m 1 … m 5 … km 1 … 1 … Ávila: 1.131 m Madrid: 655 m Sevilla: 11 m La Rinconada: 5.099 m 154 ES0000000024590 663006-Unidad 10_22593.indd 154 10/03/2015 13:21:48 Propósitos •  Desarrollar la competencia matemática resolviendo una situación de la vida real. Actividades pág. 154 1 La Rinconada: 5.099 m 5 5 5 km 1 9 dam 1 9 m • Ávila: 1.131 m 5 5 1 km 1 1 hm 1 3 dam 1 1 m • Madrid: 655 m 5 5 6 hm 1 5 dam 1 5 m • Sevilla: 11 m 5 1 dam 1 1 m 2 • 5.099 2 655 5 4.444 4.444 m 5 4 km 1 444 m • 655 2 11 5 644 644 m 5 6 hm y 44 m • 1.131 2 11 5 1.120 1.120 m 5 1 km 1 120 m • 1.131 2 655 5 476 476 m 5 4 hm 1 76 m 3 R. L. Haga una puesta en común con las altitudes buscadas por los alumnos y proponga actividades similares a las propuestas en esta página. Actividades pág. 155 1 • 4.448 • c 5 120, r 5 20 • 107.298 • c 5 95 • 140.217 • c 5 107 2 • 12 2 6 1 5 5 11 • 16 1 4 2 6 5 14 • 28 2 5 5 23 • 2 1 12 5 14 • 18 2 3 3 2 5 12 • 15 : 3 1 8 5 13 • 15 2 6 2 5 5 4 •  6 2 3 1 8 5 11 3 • 138 • 2.000 • 160 • 2.400 4 •  3 10 5 0,3 •  32 100 5 0,32 •  12 10 5 1,2 •  326 1.000 5 0,326 •  9 100 5 0,09 •  87 1.000 5 0,087 Desarrollo de la competencia matemática •  El trabajo de esta página se centra en la aplicación de todo lo aprendido en la unidad a datos de altitudes de distintas localidades. De esta manera, los alumnos comprenderán la utilidad de sus saberes y podrán desarrollar de manera adecuada esta competencia. A la hora del trabajo cooperativo, pida a los alumnos que antes de llevarlo a cabo realicen una planificación cuidadosa por escrito de todos los pasos que van a realizar: dónde van a buscar información, cómo la van a exponer a sus compañeros, de qué forma van a plantear los problemas, en qué formato expondrán los resultados… Comente esas planificaciones con los grupos. Inteligencia interpersonal 88
  • 89.
    4 Escribe enforma de fracción y en forma decimal. 3 décimas 32 centésimas 12 décimas 326 milésimas 9 centésimas 87 milésimas 5 Escribe cómo se leen de dos formas. 8,9 3,78 4,621 32,5 15,03 7,072 6 Coloca los números y calcula. 3,56 1 21,9 1 134,8 5,7 1 45,078 1 72,6 31,8 2 9,79 32 3 1,4 498,4 2 76,762 27,5 3 100 1 Calcula. 278 3 16 2.780 : 23 1.987 3 54 5.890 : 62 607 3 231 7.811 : 73 2 Calcula estas operaciones. 12 2 2 3 3 1 5 18 2 (9 : 3) 3 2 16 1 8 : 2 2 6 (6 1 9) : 3 1 8 4 3 7 2 15 : 3 15 2 (18 : 3) 2 5 12 : 6 1 4 3 3 (24 : 4) 2 3 1 8 3 Calcula la fracción de un número. 3 5 de 230 5 8 de 3.200 2 7 de 560 4 9 de 5.400 7 Para regalar a unos amigos, Marta compra un peluche por 8,90 €, una raqueta por 15,50 € y un balón por 6,80 €. ¿Cuánto gasta Marta en total? 8 En la tienda de Alberto hay 4 cajas con 6 lámparas cada una. Cada lámpara tiene 5 brazos y, en cada uno, hay 3 bombillas. ¿Cuántas bombillas en total tienen las lámparas? 9 Marcos paga una factura de 135,67 € con un billete de 100 € y otro de 50 €. ¿Cuánto dinero le sobra? ¿Cómo pueden dárselo usando el menor número de billetes y monedas posible? 10 En un teatro hay 25 filas con 15 butacas cada una y 12 filas con 8 butacas cada una. ¿Cuántas butacas en total tiene el teatro? 11 Miguel lleva en su furgoneta 15 cajas con 30 tarros de mermelada cada caja. El total lo reparte en partes iguales entre 4 supermercados. ¿Cuántos tarros de mermelada deja en cada uno? 12 En el pueblo de Natalia viven 25.000 personas. Un cuarto de las personas se dedica a la agricultura, tres quintos a la ganadería y el resto a la industria. ¿Cuántas personas se dedican a la industria? Problemas REPASO ACUMULATIVO 10 155 ES0000000024590 663006-Unidad 10_22593.indd 155 10/03/2015 13:21:50 UNIDAD 10 5 • R. M. 8 unidades y 9 décimas 8 coma 9 • 3 unidades y 78 centésimas • 4 unidades y 621 milésimas • 32 unidades y 5 décimas • 15 unidades y 3 centésimas • 7 unidades y 72 milésimas 6 • 160,26 • 123,378 • 22,01 • 44,8 • 421,638 • 2.750 7 8,90 1 15,50 1 6,80 5 31,20 Se gastó 31,20 €. 8 4 3 6 3 5 3 3 5 360 Tienen 360 bombillas. 9 150 2 135,67 5 14,33 € 1 billete de 10 €, 2 monedas de 2 €, 1 moneda de 0,20 €, 1 de 0,10 €, 1 de 0,02 € y otra de 0,01 €. 10 25 3 15 1 12 3 8 5 471 El teatro tiene 471 butacas. 11 15 3 30 5 450 450 : 4 c 5 112, r 5 2 Deja 112 tarros en cada supermercado y le quedan 2. 12 1 4 de 25.000 5 6.250 3 5 de 25.000 5 15.000 25.000 2 6.250 2 15.000 5 3.750 A la industria se dedican 3.750 personas. Notas Repaso en común • Después de que los alumnos realicen las actividades de esta página de manera individual o en pequeños grupos, pídales que expongan cuáles de ellas les han resultado más difíciles. Repase con ellos los conceptos o procedimientos implicados en esas actividades y corríjalas en común. Cada alumno o grupo, más tarde, planteará y realizará en una hoja aparte actividades similares a las dificultosas para reforzar la comprensión. 89
  • 90.
    Javi, Ana yLuis han quedado para ir a volar sus cometas. 1 Observa las cometas de cada niño y escribe en tu cuaderno la fracción que representa la zona de cada color. 2 Escribe cómo se lee la fracción que representa la zona roja de cada cometa. 3 En cada cometa, ordena de menor a mayor las fracciones que representan las zonas de cada color. 4 Copia y completa la tabla en tu cuaderno. Después, escribe cómo se lee cada número. 5 Ordena los números y utiliza el signo adecuado. 12,9 9,5 21,75 54,9 54,84 45,765 9,542 9,524 9,521 5,865 7,65 9,6 21,83 21,38 24,9 5,782 5,872 5,827 12 1 2 3 4 567 8 9 10 11 Propósitos •  Repasar los contenidos clave del trimestre. Actividades 1 Javi: 4 9 rojo, 3 9 amarilla, 2 9 azul. Ana: 3 10 rojo, 2 10 amarilla,   5 10 azul. Luis: 3 8 rojo, 1 8 amarilla, 4 8 azul. 2 Cuatro novenos. Tres décimos. Tres octavos. 3 Javi: 2 9 , 3 9 , 4 9 Ana: 2 10 , 3 10 , 5 10 Luis: 1 8 , 3 8 , 4 8 4 • 4 U 1 8 d • 3 D 1 5 U 1 6 c • 9 U 1 3 d 1 1 c 1 5 m • 4 D 1 5 U 1 7 c 1 2 m • 1 D 1 8 U 1 8 m 5 • 9,5 , 12,9 , 21,75 • 45,765 , 54,84 , 54,9 • 9,521 , 9,524 , 9,542 • 9,6 . 7,65 . 5,865 • 24,9 . 21,83 . 21,38 • 5,872 . 5,827 . 5,782 6 • 43,66 • 818,65 • 66,797 • 147,29 • 357,95 • 60,936 • 55,76 • 25,5264 • 0,9048 • 78,9 • 580 • 1.900 7 Las 7 menos veinticinco de la tarde. Repaso trimestral Javi, Ana y Luis han quedado para ir a volar sus cometas. 1 Observa las cometas de cada niño y escribe en tu cuaderno la fracción que representa la zona de cada color. 2 Escribe cómo se lee la fracción que representa la zona roja de cada cometa. 3 En cada cometa, ordena de menor a mayor las fracciones que representan las zonas de cada color. 4 Copia y completa la tabla en tu cuaderno. Después, escribe cómo se lee cada número. 5 Ordena los números y utiliza el signo adecuado. 12,9 9,5 21,75 54,9 54,84 45,765 9,542 9,524 9,521 5,865 7,65 9,6 21,83 21,38 24,9 5,782 5,872 5,827 Javi Ana Luis De menor a mayor De mayor a menor JAVI ANALUIS Parte entera Parte decimal Decenas Unidades Décimas Centésimas Milésimas 4,8 35,06 9,315 45,072 18,008 156 ES0000000024590 663006-Repaso2_22594.indd 156 10/03/2015 13:21:15 90
  • 91.
    SEGUNDO TRIMESTRE 12 1 2 3 4 567 8 9 10 1112 1 2 3 4 567 8 9 10 1112 1 2 3 4 567 8 9 10 11 12 1 2 3 4 567 8 9 10 1112 1 2 3 4 567 8 9 10 11 6 Calcula. 34,9 1 8,76 754,9 1 63,75 9,845 1 56,952 231,89 2 84,6 432,9 2 74,95 70,5 2 9,564 32,8 3 1,7 5,318 3 4,8 6,032 3 0,15 7,89 3 10 5,8 3 100 1,9 3 1.000 7 Escribe la hora de cada reloj digital tal como se lee en un reloj de agujas. ¿Qué hora marcará cada reloj cuando hayan pasado 2 horas y 25 minutos? 8 Expresa en la unidad que se indica. 2 m, 5 dm y 7 cm 4 m, 6 dm y 9 cm 5 m y 8 dm 1 m, 2 cm y 9 mm 3 m y 7 mm 5 m, 7 dm y 8 cm 2 km, 3 hm y 4 dam 3 km, 5 hm y 6 m 6 km y 5 dam Problemas 9 Resuelve. Para envolver regalos, Lucía tiene un rollo de cinta de 3,5 m. Primero cortó 0,75 m y después cortó 1,55 m. ¿Cuántos metros de cinta le quedan en el rollo? Arturo compra 3 CD de música a 8,95 € cada uno y un libro por 14,50 €. Para pagar entrega un billete de 50 €. ¿Cuánto dinero le devuelven? Nuria tiene en su puesto 350 helados. Hoy ha vendido dos quintos de los helados a 1,50 € cada uno. ¿Cuánto ha recaudado Nuria por esta venta? Todos los días, un tren sale de la estación a las 9 menos cuarto de la mañana y tarda 3 horas y media en llegar a su destino. Hoy el tren ha salido con 25 minutos de retraso y ha tardado 4 horas y cuarto en llegar a su destino. ¿A qué hora ha salido de la estación? ¿A qué hora ha llegado a su destino? Representa las horas en un reloj de agujas y en un reloj digital. 18:35 13:40 22:50 157 En centímetros En milímetros En metros ES0000000024590 663006-Repaso2_22594.indd 157 10/03/2015 13:21:17 Las 2 menos veinte de la tarde. Las 11 menos diez de la noche. • Las 9 de la noche. Las 4 y cinco de la tarde. La 1 y cuarto de la mañana. 8 • 257 cm • 469 cm • 580 cm • 1.029 mm • 3.007 mm •  5.780 • 2.340 m • 3.506 m • 6.050 m 9 • 3,5 2 0,75 2 1,55 5 1,2 Le quedan 1,2 m. • 3 3 8,95 1 14,50 5 41,35 50 2 41,35 5 8,65 Le devuelven 8,65 €. • 2/5 de 350 5 140 140 3 1,50 5 210 Ha recaudado 210 €. • 8:45 1 25 5 9:10 Ha salido a las 9 y diez. 9:10 1 4:15 = 13:25 Ha llegado a la 1 y veinticinco de la tarde. Compruebe que los alumnos representan las horas correctamente. Notas 91
  • 92.
  • 93.
  • 94.
  • 95.