Este documento presenta un libro de matemáticas para primaria que forma parte del proyecto La Casa del Saber. El libro tiene como objetivos preparar a los alumnos para la educación secundaria desarrollando conocimientos fundamentales, aplicar las matemáticas a la vida cotidiana y trabajar las matemáticas de forma global y eficaz. El proyecto pretende que los alumnos reconozcan la diversidad cultural.












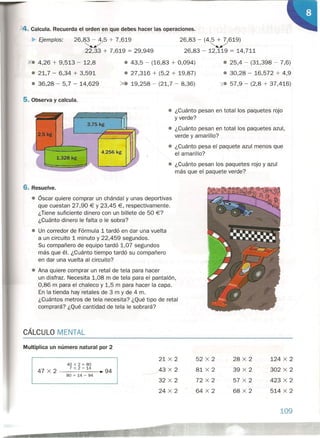
![Actividades
]{1. Descompón cada número y escribe
cómo se lee.
.70.421
.682.093
.2.407.516
• 39.210.008
• 265.074.300
x. 823.609.050
~2. Escribe con cifras estos números.
• Cuarenta y cinco millones treinta mil
doscientos siete.
• Tres millones quinientos catorce mil
ochenta.
• Seiscientos veintisiete millones ciento
sesenta y tres mil.
• Trescientos millones dos mil cien.
i. Setenta y nueve millones trescientos mil
cuatrocientos noventa y uno.
X3. Escribe el valor en unidades de la cifra 3 en
cada número de la actividad 2.
4. Observa el número de habitantes de estas
ciudades y contesta.
~. I .,
Bombay (India)
12.600.000 hab.
Moscú (Rusia)
11.300.000 hab.
Buenos Aires (Argentina)
11.920.000 hab.
Shanghai (China)
13.300.000 hab.
11 ¿Cuál de estas ciudades es la más
poblada? ¿Y la menos poblada? .
• ¿Cuántos habitantes tiene Bombay más
que Buenos Aires?
14
5. ESTUDIO EFICAZ. Copia y completa el
•
• esquema.
•
• ORDEN EN LAS OPERACIONES COMBINADAS
•
•
• ¡----1.0Calcular los ...
• f-- 2.° ...
•
• '-- 3.° ...
X6. Calcula
•
.20 - (8 + 5) '!.e 16 - 7 + (9 - 3)
• .6+ 3 X 10 "".3x7-8x2
•
• • (15 - 3) : 4 • (5 + 4) X (6 - 1)
• - 10 X 6 : 5 (!)14 - 4 X 3 + 7
• 09 - (5 + 13) : 6• • 18 : (7 + 2)
• -5x8-6 C!)20 : 4 X 3 + 8
(!) Elige una de las siguientes opciones, expresa
numéricamente cada frase y calcula.
•
•
d. O - (O + O)
e.O X (O + O)
f. O: (O - O)
a.O - O + O
b. O X O + O
c.O:O -O
•
•
•
•
•
• ~. A 15 le resto la suma de 6 y 4.
• d. 15 - (6 + 4) = ...
ie A 7 le resto 2 y luego le sumo 5.
~. Multiplico 10 por la suma de 5 y 2.
• Divido 12 entre la diferencia de 7 y 4.
;- Al doble de 8 le sumo 3.
- A la mitad de 14 le resto 5.
•
•
•
•
•
•
•
r:8. ,scribe los números en su lugar para que las
dos expresiones sean ciertas.
•
000
~
• O - (o + o) = 2
000 -0-0+0=5
000
~
• O X (o - o) = 15
000 -o + O X O = 12
•
•
•
•](https://image.slidesharecdn.com/matematicas6-150309151108-conversion-gate01/85/Matematicas-6-Primaria-14-320.jpg)





































































![Actividades'
X.1. ¿Qué fracciones puedes escribir en forma de
número mixto? Escríbelas y explica por qué
con las otras no es posible.
9 7 15 10 4 23
- - - - - .)
- •2--8 4 5 9 7
•
•
,2. Escribe. •
•
•Enforma de número mixto
•
21 39 28 37
x58
- - - ,>(84 6 9 7
•
Enforma de fracción •
•
3 2 7 4 6
6- 3- 2- 'X. 7 - x5-
5 7 8 6 9
•
@. Averigua si las fracciones de cada pareja son •
•equivalentes o no.
1 5
• -y-
4 20
5 15
• -y-
8 32
24 8
• -y-
9 3
')4. Completa las fracciones para que sean
equivalentes y contesta.
2 ld 3 [] 4 24
j- ==- /,-==- ---
7 O 8. 32' 9 O
4 O 15 5 15 O- - - ---
lO 5 27 O 35 7
~ ¿Por qué número has multiplicado
o dividido cada término de la primera
fracción para obtener la segunda?
).5. Escribe dos fracciones equivalentes a cada
fracción: una por amplificación y otra por
simplificación. •
8
J 12
10
40
5
30
21
14
'x 6. Calcula la fracción irreducible de cada una
de estas fracciones.
8
6
25
10
32
12
30
18
36
27
88
-~
• 7. Reduce a común denominador.
•
• • Por el método de los productos cruzados.
4 5
-y-
5 8
15 9
-y-
7 4
• Por el método del m.c.m.
7 9
'4Y8
3 7 5
-'-y-
8 12 6
8 10
-y-
6 9
4 7
15 Y 30
~8.ESTUDIO EFICAZ. Completa el esquema en
tu cuaderno.
COMPARACiÓN DE FRACCIONES
1-- Con igual denominador ~ Es mayor ...
f-- Con igual ...
'-- Con distinto ...
• .(9. Ordena de menor a mayor.
• 9 9 7
• -, -y-
4 6 9
5 11 14
• -, - y-
3 5 15
•
•
•
• 10. Escribe las fracciones de la pizarra
• que cumplen cada condición.
•
2
• 2 1
• Mayores que 5'
• - 2 -
7
-
3• 3 3
• 3 3 • Menores que y'8 -
• - -
5
• 10 12 4
• • Iguales que 6'
•
• 11. Compara cada pareja de números.
•
• 9
• ~ Ejemplo: 2 y 4
•
• 8 8 9 9
2 = -' - < - ~ 2<-
• 4'4 4 4
•
• 10 25 17 14
.5y- .6y- • - y3 • - y2
• 3 4 6 5](https://image.slidesharecdn.com/matematicas6-150309151108-conversion-gate01/85/Matematicas-6-Primaria-88-320.jpg)
























































![OPERACIONES
1. Calcula.
7 .5
-+-
4 6
9 11
-+-
10 15
7
-+4
4
3 7 5
-+-+ -
4 9 12
9 7
---
8 10
5 13
---
6 18
20
- -5
3
8 _ 21
4
2 3
-X-
5 7
9 5
-X-
4 6
3
- X 7
8
10
6X -
17
2. Recuerda el orden en que debes hacer las operaciones y calcula.
7 5 3 8 1 3
15 _ (3 + ~)
(; - ~) X ~
3 (5 7 )-+-X- --_.-
2": 8 + 1210 6 5 9 5'7 16 8 5
3. Calcula.
0,359 + 8,671 9,524 - 3,576 3,68 X 9 25,9: 7
7,286 + 19,45 20,3 - 8,57 4,53 X 7,2 675 : 5,4
3,14 + 2,6 + 5,973 5,6 - 1,924 2,805 X 5,6 9,052: 8,3
4. Recuerda el orden en que debes hacer las operaciones y calcula .
• 65,14 + 9,282 : 2,6
• 4,81 X 3,7 - 5,29
5 4
6"7
2 5
9"8
30
-:4
7
12
9"-
" 5
• 58,548 : (4,3 + 2,67) X 5,06
• 23,74 + 19,812 : (5,4 - 2,86)
5. Divide, obteniendo en el cociente tantas cifras decimales como se indica.
Tres cifras
decimales
25,1: 9,3
1,498 : 0,427
Una cifra
decimal
•.
9: 2,6
72,2: 7,6
Dos cifras
decimales
23,4 : 15
18,32: 4,5
6. Expresa cada fracción como un número decimal.
rE rn [i] I~I 1~11
CÁLCULO MENTAL
29 + 17
48 + 23
57 + 35
31 + 46
62 + 24
34 - 19
62 - 38
75 - 57
49 - 21
58 - 42
34 X 2
56 X 2
423 X 2
84 X 5
56 X 5
25 X 11
43 X 11
56 X 101
17 X 9
28 X 99
149
-----------------------------------------------------------------------------~](https://image.slidesharecdn.com/matematicas6-150309151108-conversion-gate01/85/Matematicas-6-Primaria-149-320.jpg)
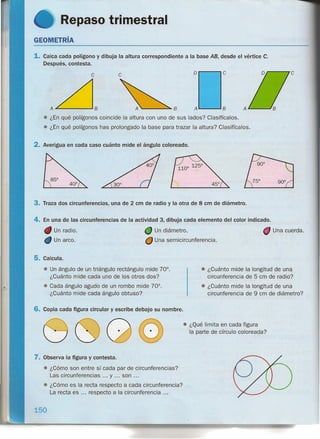














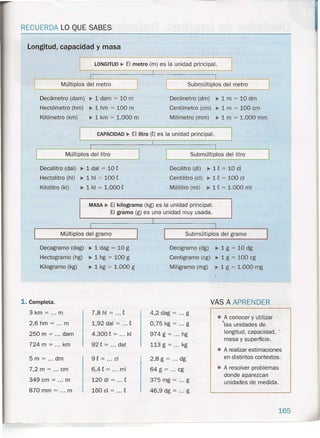








![Relaciones entre unidades de supeñicie
En el cuadro están las unidades de superficie y las relaciones entre ellas.
Para pasar de una unidad a otra menor se multiplica
Para pasar de una unidad a otra mayor se divide
FÍjate en cómo pasamos de una unidad a otra en estos ejemplos.
x 10.000
0,6 darrr' = 0,6 x 10.000 = 6.000 drrr'
• De cm+a darrf j- ~ •• :100 [2] ..:100 ~ ••;100 ~
: 1.000.000
,.
3.800 cm" = 3.800 : 1.000.000 = 0,0038 darrf
1. Completa.
0,005 hm2
= ... darrf
136 hrrr' = ... km2
7.520 darrf = ... km2
0,93 km2
= ... darn"
8,4 dm2
= rnrn"
12,5 cm" = dm2
1,95 cm" = mrrf
714 rnrn" = .:. dm2
974 drn" = ... darn"
1,06 darrf = cm"
2.300 drrr' = hm2
28.130 cm" = darrf
2. Expresa en la unidad indicada.
2 darrf y 1.750 m2
3. Resuelve .
.• Paula tiene una tarjeta de cartulina de 0,5 dm". Ha dibujado en ella un rectángulo rojo de 28 cm"
y lo ha recortado. ¿Cuántos centímetros cuadrados de cartulina le han sobrado?
.•.74](https://image.slidesharecdn.com/matematicas6-150309151108-conversion-gate01/85/Matematicas-6-Primaria-174-320.jpg)



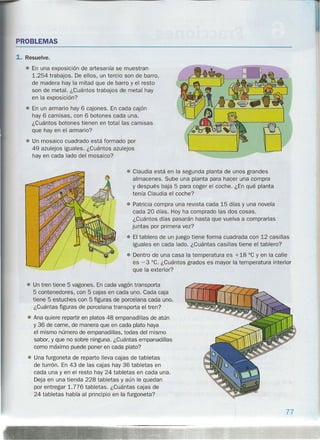
![Solución de problemas
Representar gráficamente la situación
En muchos problemas, representar el enunciado te ayudará a entenderlo mejor.
Resuelve estos problemas haciendo un dibujo aproximado del enunciado.
María es bióloga. Ha medido la cabeza, el tórax y el abdomen
de una avispa. La longitud del tórax es el doble
de la longitud de la cabeza y la longitud del abdomen
es el triple de la longitud de la cabeza. La avispa mide 12 mm.
¿Cuánto mide cada parte de su cuerpo?
~ Representamos la situación con un dibujo. La cabeza
la dibujamos con un segmento. Para el resto de partes
repetimos ese segmento tantas veces como indica
el enunciado. La avispa es la suma de las tres partes.
[ Cabeza ] [ Tórax ] [ Abdomen]
H
Avispa
> I I
•• ~
12 mm
En la avispa hay 6 partes de igual longitud, y en total mide 12 mm.
Cada una de las partes mide 12 mm : 6 = 2 mm.
Cabeza ~ 1 parte, mide 1 x 2 mm = 2 mm.
Tórax ~ 2 partes, mide 2 x 2 mm = 4 mm.
Abdomen ~ 3 partes, mide 3 x 2 mm = 6 mm.
Solución: La cabeza mide 2 mm; el tórax, 4 mm; y el abdomen, 6 mm.
1. Marta tiene un vaso, una botella y una jarra. La capacidad de la botella es el triple
de la capacidad del vaso y la de la jarra, el doble de la capacidad de la botella.
La capacidad total de los tres recipientes es 250 el. ¿Qué capacidad tiene cada uno?
2. Mónica, Paula y Juan son primos. Paula mide el doble que Mónica y Juan mide
el doble que Paula. La suma de sus alturas es 315 cm. ¿Cuánto mide cada uno?
3. Pedro compró una nevera en tres plazos. En el segundo plazo pagó el doble que
en el primero y en el tercer plazo pagó el doble que en los dos anteriores juntos.
La nevera costó 810 €. ¿Cuánto pagó en cada plazo?
4. INVENTA. Escribe un problema, similar a los de esta página, que se resuelva
más fácilmente haciendo un dibujo de la situación.
178](https://image.slidesharecdn.com/matematicas6-150309151108-conversion-gate01/85/Matematicas-6-Primaria-178-320.jpg)



















![Volumen con un cubo unidad
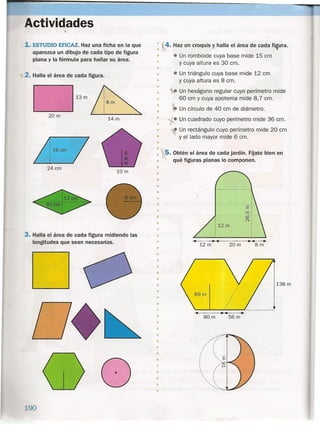
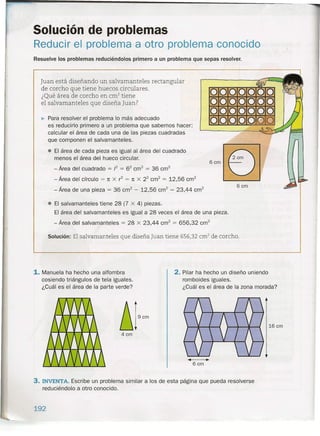
El volumen de un cuerpo es la cantidad de espacio que ocupa.
En este curso se calculará el volumen de cubos y ortoedros
(un ortoedro es un prisma cuyas caras son todas rectángulos).
Ortoedro
Para hallar el volumen de un ortoedro o un cubo, se toma como unidad
de medida un cubito y se cuenta el número de cubitos de cada cuerpo.
/
/
/
1/
Cada capa de este ortoedro
tiene 4 x 2 cubitos.
El ortoedro tiene
3 capas de alto.
Hay 4 x 2 x 3 = 24 cubitos.
Volumen = 24 ljJ
Cada capa de este cubo
tiene 2 x 2 cubitos. ~
El cubo tiene 2 capas de alto. ,
Hay 2 x 2 x 2 = 23
= 8 cubitos.
Volumen = 8. LJ)
1. Cuenta los cubitos y calcula el volumen.
A
)2. Calcula el volumen del ortoedro usando cada cubo unidad.
Unidad
Volumen = .....
~ ~-:---:'.~:::.-~~7:]
~~ • _'- _~ ~••_.-!-. ~iH
Unidad
Volumen = ...
• ¿Por qué los valores numéricos que obtienes son distintos?
200](https://image.slidesharecdn.com/matematicas6-150309151108-conversion-gate01/85/Matematicas-6-Primaria-200-320.jpg)