Este documento presenta las soluciones a pruebas y ejercicios de matemáticas del primer semestre de 1999. Contiene las respuestas a 4 pruebas distintas con ejercicios de álgebra, trigonometría, funciones y ecuaciones. Además, incluye las soluciones a 10 guías de ejercicios de funciones cuadráticas, trigonométricas y raíces cuadradas. Por último, presenta figuras gráficas que ilustran las soluciones.








![´
1.2. MATEMATICAS I - PRUEBA NO 2 FORMA 1 9
1.2 Matem´ticas I - Prueba No 2 forma 1
a
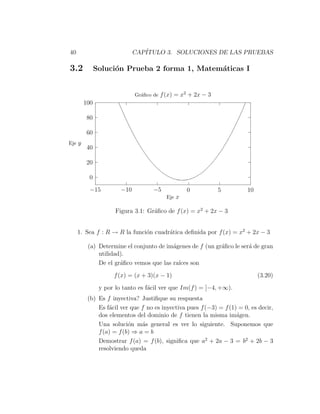
1. Sea f : R → R la funci´n cuadr´tica definida por f (x) = x2 + 2x − 3
o a
(a) Determine el conjunto de im´genes de f (Ind: Un gr´fico le ser´
a a a
de gran utilidad).
(b) ¿Es f inyectiva? Justifique su respuesta
(c) Encuentre el intervalo m´s grande I, de n´meros positivos, en que
a u
f es inyectiva
(d) Calcule f −1 (x) para x ∈ J = f (I)
2. Un observador ve un globo aerost´tico, que se eleva verticalmente, bajo
a
o
un ´ngulo de elevaci´n de 30 despu´s de 2 minutos, el ´ngulo de ele-
a o e a
vaci´n es de 60o . En un principio la distancia entre el observador y el
o
globo era de 200 metros.
(a) ¿A que distancia est´ el observador del punto de lanzamiento del
a
globo?
(b) Si los ojos del observador est´n a 1,7 metros del suelo, ¿a que
a
altura se encuentra el globo al cabo de los dos minutos?
3. Resuelva la ecuaci´n trigonom´trica
o e
1
− sin x cos x = 0
2
en el intervalo [−π, 5π]
√ √ √
2 2 3 i
4. Dados los n´meros complejos z1 =
u 2
+i 2
y z2 = 2
+ 2
(a) Escriba z1 y z2 en forma polar o trigonom´trica
e
z1
(b) Encuentre z2
(c) Calcule ( z1 )8
z2](https://image.slidesharecdn.com/librowilcken-120915205117-phpapp01/85/Librowilcken-9-320.jpg)
![10 CAP´
ITULO 1. PRUEBAS PRIMER SEMESTRE 1999
1.3 Matem´ticas I - Prueba No 2 forma 2
a
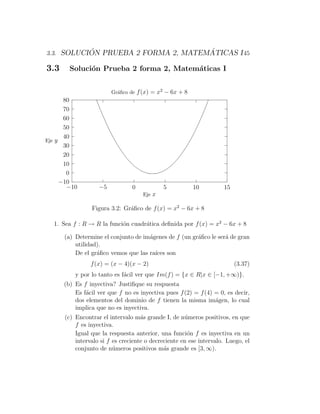
1. Sea f : R → R la funci´n cuadr´tica definida por f (x) = x2 − 6x + 8
o a
(a) Determine el conjunto de im´genes de f (Ind: Un gr´fico le ser´
a a a
de gran utilidad).
(b) ¿Es f inyectiva? Justifique su respuesta
(c) Encuentre el intervalo m´s grande I, de n´meros positivos, en que
a u
f es inyectiva
(d) Calcule f −1 (x) para x ∈ J = f (I)
2. Resuelva la ecuaci´n trigonom´trica
o e
1
− cos x sin x = 0
2
en el intervalo [−π, 5π]
√ √ √
1 3 2 2
3. Dados los n´meros complejos z1 =
u 2
+i 2
y z2 = 2
+i 2
(a) Escriba z1 y z2 en forma polar o trigonom´trica
e
z1
(b) Encuentre z2
z1
(c) Calcule ( z2 )8
4. Un observador ve un globo aerost´tico, que se eleva verticalmente, bajo
a
o
un ´ngulo de elevaci´n de 30 despu´s de 2 minutos, el ´ngulo de ele-
a o e a
o
vaci´n es de 60 . En un principio la distancia entre el observador y el
o
globo era de 300 metros.
(a) ¿A que distancia est´ el observador del punto de lanzamiento del
a
globo?
(b) Si los ojos del observador est´n a 1,6 metros del suelo, ¿a que
a
altura se encuentra el globo al cabo de los dos minutos?](https://image.slidesharecdn.com/librowilcken-120915205117-phpapp01/85/Librowilcken-10-320.jpg)




![2.1. GU´ NUMERO 1
IA ´ 15
3. Observe que
1 1
1− =
2 2
1 1 1
1− 1− =
2 3 3
1 1 1 1
1− 1− 1− =
2 3 4 4
Deduzca una ley general y demu´strela por inducci´n.
e o
4. Usando propiedades de las sumatorias demuestre las f´rmulas:
o
n
n(n + 1)
(a) i=
i=1 2
n 2
Sugerencia, considere la sumatoria i=1 [i − (i + 1)2 ]
n
n(n + 1)(2n + 1)
(b) i2 =
i=1 6
n 3
Sugerencia, considere la sumatoria i=1 [i − (i + 1)3 ]
Calcule adem´s n i3 ;
a i=1
n 4
i=1 i ;
n
i=1 i
5
5. Calcule y pruebe su respuesta usando inducci´n
o
n
1 1
(a) −
i=1 i+1 i
n
1 1
(b) −
i=1 i + 2 i
Para esta ultima parte considere la siguiente igualdad:
´
1 1 1 1 1 1
− = − + −
i+2 i i+2 i+1 i+1 i](https://image.slidesharecdn.com/librowilcken-120915205117-phpapp01/85/Librowilcken-15-320.jpg)





![2.5. GU´ NUMERO 5
IA ´ 21
2.5 Gu´ n´ mero 5
ıa u
1. Un rect´ngulo tiene 200 [cm] de per´
a ımetro. Expresar su ´rea como
a
funci´n de x.
o
2. Vamos a construir una caja abierta con una pieza cuadrada de metal de
16 [cm] de lado, cortando cuadrados iguales de sus esquinas y doblando
por las l´
ıneas de puntos (ver figura). Exprese el volumen V en funci´n
o
de x.
√
3. Un rect´ngulo est´ acotado por el eje X y el semicirculo y = 16 − x2
a a
(ver figura). Escriba el ´rea A del rect´ngulo como funci´n de x.
a a o
4. Una caja cerrada de secci´n cuadrada de lado x tiene un ´rea de
o a
2
200[cm ] (ver figura). Exprese el volumen V como funci´n de x.
o
√
5. Dadas las funciones f (x) = 2x − 3 y g(x) = x + 1. Encuentre
(a) Dom(f ), Dom(g)
(b) f + g
(c) f · g
(d) f ◦ g
(e) g ◦ f
y los respectivos dominios.
6. Determine si las siguientes funciones son inversas una de la otra:
x+3
(a) f (x) = 2x + 3 g(x) = 2
√ 2
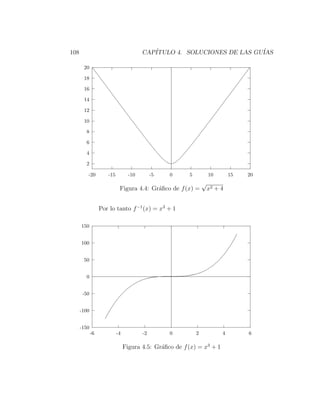
(b) f (x) = x − 4 g(x) = x + 4 x ≥ 0
√
(c) f (x) = 1 − x3 g(x) = 3 1 − x
1
(d) f (x) = x−2 ,x > 0 g(x) = x− 2 ,x > 0
1 1−x 1
(e) f (x) = x2 +1
g(x) = x
en ] 2 , 1[
7. Encuentre la funci´n inversa (si existe). Represente aproximadamente
o
un gr´fico de f y de f −1
a
(a) f (x) = x2 x≥0](https://image.slidesharecdn.com/librowilcken-120915205117-phpapp01/85/Librowilcken-21-320.jpg)









![2.10. GU´ NUMERO 10 (EJERCICIOS PROPUESTOS)
IA ´ 31
2.10 Gu´ n´ mero 10 (Ejercicios Propuestos)
ıa u
1. Dada f (x) = 5 − encuentre los c ∈]1, 4[ tales que f (c) = f (4)−f (1)
4
x 4−1
√
2. Considere la funci´n f (x) = x en el intervalo [1, 9]. Dibuje
o
(a) Encuentre la ecuaci´n de la secante que pasa por (1, f (1)) y
o
(9, f (9))
(b) Calcular el valor c ∈]1, 9[ para el cual f (c) = f (9)−f (1) . Encuentre
9−1
la ecuaci´n de la recta tangente a la gr´fica de f en el punto
o a
(c, f (c))
3. Sea f (x) = 1 − x2/3 . Pruebe que f (1) = f (−1) = 0, pero que f (x)
nunca es cero en [−1, 1]. Explicar por qu´ este resultado no contradice
e
el teorema de Rolle.
4. Vea que las siguientes funciones satisfacen el Teorema de Rolle y en-
cuentre los puntos c que satisfacen las conclusiones del teorema
(a) f (x) = 9x2 − x4 en [−3, 3]
1−x2
(b) f (x) = 1+x2
en [−1, 1]
5. Pruebe que f (x) = (x − 1)2/3 satisface la hip´tesis del T.V.M. en [1, 2]
o
y encuentre c ∈]1, 2[ que satisfacen la conclusi´n del mismo.
o
6. Si f (x) = x2 − 5x + 2. Encuentre las funciones F tales que F = f .
Al graficarlas ¿que propiedades tienen estas funciones? ¿Habr´ alguna
a
π
funci´n F tal que F (8) = √2 ?
o
7. Sea F : C → C funci´n definida por F (z) = F (x + yi) = x2 + 2xy + y 2 .
o
Para cada y = a fijo hay fa funci´n real tal que fa (x) = x2 + 2ax + a2 .
o
df
Calcule dx
8. Encuentre los puntos cr´ıticos de f si los hay. Encuentre los intervalos
abiertos donde f es creciente o decreciente.
(a) f (x) = (x − 1)2/3
(b) f (x) = x3 − 6x2 + 15
(c) f (x) = x4 − 2x3](https://image.slidesharecdn.com/librowilcken-120915205117-phpapp01/85/Librowilcken-31-320.jpg)
![32 CAP´
ITULO 2. GU´ DE EJERCICIOS ANO 1999
IAS ˜
x
(d) f (x) = x+1
9. La concentraci´n C de cierto producto qu´
o ımico en la sangre, t horas
despu´s de ser inyectado en el tejido muscular viene dado por
e
3t
C(t) =
27 + t3
¿Cu´ndo es m´xima la concentraci´n?
a a o
10. Al nacer un beb´ perder´ peso normalmente durante unos pocos d´
e a ıas
y despu´s comenzar´ a ganarlo. Un modelo para el peso medio W de
e a
los beb´s durante las 2 primeras semanas de vida es P (t) = 0.015t2 −
e
0.18t + 3.3. Hallar los intervalos de crecimiento y de decrecimiento de
P
11. Calcular las dimensiones del mayor rect´ngulo inscrito en un c´
a ırculo de
radio r
12. Una p´gina rectangular ha de contener 96[cm2 ] de texto. Los m´rgenes
a a
superior e inferior tienen 3[cm] de ancho y los laterales 2[cm] ¿Qu´e
dimensiones de la p´gina minimizar´n la cantidad de papel requerida?
a a
√
13. Considere la funci´n f (x) = x en el intervalo [1, 9]. Dibuje. Calcular
o
el valor c ∈]1, 9[ para el cual se cumple f (c) = f (9)−f (1) y encuentre la
9−1
ecuaci´n de la recta tangente a la gr´fica de f en el punto (c, f (c)).
o a
14. Dada f (x) = 2x5/3 − 5x4/3 . Calcule f (x) y f (x). Encuentre si los hay
puntos cr´
ıticos, intervalos de crecimiento y decrecimiento, m´ximos y
a
m´ınimos. Intersecciones de f (x) con los ejes coordenados. Dibuje.
15. Solucione el problema anterior para
x 2
(a) f (x) = √ f (x) =
x2+2 (x2 + 2)3/2
−6x
f (x) =
(x2 + 2)5/2](https://image.slidesharecdn.com/librowilcken-120915205117-phpapp01/85/Librowilcken-32-320.jpg)



![36 CAP´
ITULO 3. SOLUCIONES DE LAS PRUEBAS
3.1 Soluci´n Prueba 1 MatI
o
1. (a) |3x + 4| + |x − 4| ≥ 20 (3.1)
Primero, encontremos los puntos cr´
ıticos
3x1 + 4 = 0
3x1 = −4
4
x1 = − (3.2)
3
x2 − 4 = 0
x2 = 4 (3.3)
4
Debemos primero evaluar la expresi´n (3.1) para x ≤ − 3
o
−(3x + 4) − (x − 4) ≥ 20
−3x − 4 − x + 4 ≥ 20
−4x − 4 + 4 ≥ 20
−4x ≥ 20
x ≤ −5 (3.4)
4
Ahora, debemos hacer lo mismo para los x ∈ (− 3 , 4)
(3x + 4) − (x − 4) ≥ 20
3x + 4 − x + 4 ≥ 20
2x + 8 ≥ 20
2x ≥ 12
x ≥ 6 (3.5)
Por ultimo debemos evaluar (3.1) para x ≥ 4
´
(3x + 4) + (x − 4) ≥ 20
4x ≥ 20
x ≥ 5 (3.6)
Por lo tanto, los intervalos en donde (3.1) tiene soluci´n son:
o
S1 = (−∞, −5] S2 = φ S3 = [5, ∞)](https://image.slidesharecdn.com/librowilcken-120915205117-phpapp01/85/Librowilcken-36-320.jpg)
![´
3.1. SOLUCION PRUEBA 1 MATI 37
Entonces la soluci´n ser´:
o a
S = S1 ∪ S2 ∪ S3 = (−∞, −5] ∪ [5, ∞) (3.7)
(b) Resolvamos (x − 3)(x + 4) ≤ 2x2 − 5x − 10
Para ello encontremos los ceros de la desigualdad
(x − 3)(x + 4) ≤ 2x2 − 5x − 10
x2 + x − 12 ≤ 2x2 − 5x − 10
0 ≤ x2 − 6x + 2 (3.8)
Ahora usando que la soluci´n de una ecuaci´n cuadr´tica es
o o a
√
−b ± b2 − 4ac
x1/2 = (3.9)
2a
Usando esto en la ecuaci´n (8) obtenemos
o
√ √ √
6 ± 36 − 8 6 ± 28 6±2 7 √
x1/2 = = = = 3 ± 7(3.10)
2 2 2
Por lo tanto tenemos
√ √
0 ≤ (x − (3 + 7))(x − (3 − 7)) (3.11)
Por lo tanto la soluci´n ser´
o ıa
√ √
S = (−∞, 3 − 7] ∪ [3 + 7, ∞) (3.12)
2. (a) Calcular
n n n
(7 + 5k) = 7+ 5k
k=1 k=1 k=1
n n
= 7 +5 k
k=1 k=1
n(n + 1)
= 7n + 5
2
5n2 5n
= 7n + +
2 2
2
5n + 5n + 14n
=
2
5n2 + 19n
= (3.13)
2](https://image.slidesharecdn.com/librowilcken-120915205117-phpapp01/85/Librowilcken-37-320.jpg)


![´ ´
3.2. SOLUCION PRUEBA 2 FORMA 1, MATEMATICAS I 41
a2 − b2 + 2(a − b) = 0
(a + b)(a − b) + 2(a − b) = 0
(a − b)[(a + b) + 2] = 0 (3.21)
Esto nos da dos soluciones, a = b, o bien, a = −2 − b, lo cual dice
que f no es inyectiva, i.e. f (a) = f (b) no implica necesariamente
que a = b.
(c) Encuentre el intervalo m´s grande I, de n´meros positivos, en que
a u
f es inyectiva.
Para que una funci´n f sea inyectiva en un intervalo, la funci´n f
o o
debe ser creciente o bien decreciente, luego el intervalo son todos
los Reales positivos pues ah´ la funci´n es creciente.
ı o
(d) Calcule f −1 (x) para x ∈ J = f (I)
J = f (I) = { de todos los reales mayores o iguales a − 3}
Luego es f´cil ver que la preim´gen de este conjunto es el conjunto
a a
S = (−∞, −2] ∪ [0, +∞)
2. (a) Sea D la distancia que est´ el observador del punto de lanzamiento
a
del globo, entonces tenemos
D
sin(30) = ⇒ D = 200 sin(30)
200 √
3
D = 200
2 √
D = 100 3 (3.22)
(b) Es f´cil ver que la altura inicial (H) era de
a
H
cos(30) = ⇒ H = 200 cos(30)
200
1
H = 200
2
H = 100 (3.23)](https://image.slidesharecdn.com/librowilcken-120915205117-phpapp01/85/Librowilcken-41-320.jpg)
![42 CAP´
ITULO 3. SOLUCIONES DE LAS PRUEBAS
¯
Para encontrar la altura final (H) tenemos que
D ¯ D
tan(60) = ¯ ⇒H =
H tan(60)
¯ D
H = 1
√
3
√
¯ 100 3
H = 1
√
3
¯
H = 300[m] (3.24)
Luego, la altura al suelo es 300 + 1, 7 = 301, 7[m]
3. Reolver
1
− sin x cos x = 0 (3.25)
2
El producto de dos n´meros natirales es igual a cero si cada uno de los
u
n´meros es igual a cero. Por lo tanto, tenemos que
u
1
cos x = 0 o bien − sin x (3.26)
2
Pero cos(x) = 0 si x ∈ {− 3π , − π , π , 3π , 5π , 7π , 9π , etc.}
2 2 2 2 2 2 2
Luego, los valores que se encuentran en el intervalo pedido son
π π 3π 5π 7π 9π
x∈ − , , , , , (3.27)
2 2 2 2 2 2
Ahora hay que ver las soluciones de sin(x) = 1 , estos valores son
2
2π π 4π 7π 10π 13π
x∈ − , , , , , (3.28)
3 3 3 3 3 3
√ √ √
2 2 3 i
4. Sean z1 = 2
+i 2
y z2 = 2
+ 2](https://image.slidesharecdn.com/librowilcken-120915205117-phpapp01/85/Librowilcken-42-320.jpg)


![46 CAP´
ITULO 3. SOLUCIONES DE LAS PRUEBAS
(d) Calcule f −1 (x) para x ∈ J = f (I)
La preim´gen de este conjunto son claramente todos los reales.
a
2. Reolver
1
− cos(x) sin(x) = 0 (3.38)
2
El producto de dos n´meros natirales es igual a cero si cada uno de los
u
n´meros es igual a cero. Por lo tanto, tenemos que
u
1
sin(x) = 0 o bien − cos(x) (3.39)
2
Para sin(x) = 0 el conjunto de soluciones en [−π, 5π] ser´
a
x∈ − π, 0, π, 2π, 3π, 4π, 5π (3.40)
1
El conjunto de valores de cos(x) = 2
ser´
a
5π π 7π 13π 17π 23π 29π
x∈ − , , , , , , (3.41)
6 6 6 6 6 6 6
√ √ √
1 3 2 2
3. Dados los n´meros complejos z1 =
u 2
+i 2
y z2 = 2
+i 2
(a) Escribir z1 y z2 en forma polar o trigonom´trica.
e
Para esto debemos ver los ´ngulos y m´dulos de estos complejos.
a o
√
1 2 2 2
|z1 | = +
2 2
1 3
= +
4 4
4
=
4
√
= 1
|z1 | = 1 (3.42)](https://image.slidesharecdn.com/librowilcken-120915205117-phpapp01/85/Librowilcken-46-320.jpg)

![48 CAP´
ITULO 3. SOLUCIONES DE LAS PRUEBAS
(c) Calculemos ahora ( z1 )8
z2
8 8
z1 π
= e−i 12
z2
π
= e−i8 12
2π
= e−i 3 (3.49)
4. (a) Sea D la distancia que est´ el observador del punto de lanzamiento
a
del globo, entonces tenemos
D
sin(30) = ⇒ D = 300 sin(30)
300 √
3
D = 300
2 √
D = 150 3 (3.50)
(b) Para ver la altura del globo a los 2 minutos tenemos que
D
tan(60) = ¯ (3.51)
H
¯
donde H es la altura desconocida.
Luego
√
¯ = D 150 3
H = 1 = 150 · 3 = 450 (3.52)
tan(60) 3
Ahora a esta altura debemos agregarle la altura de los ojos del
observador que es 1, 6[m], por lo tanto la altura ser 451, 6[m].](https://image.slidesharecdn.com/librowilcken-120915205117-phpapp01/85/Librowilcken-48-320.jpg)

![50 CAP´
ITULO 3. SOLUCIONES DE LAS PRUEBAS
(b) Para encontrar la recta tangente que pasa por el punto x = 1
debemos primero derivar f (x)
f (x) = 15x4 − 105x2 + 180 (3.56)
A continuaci´n debemos evaluar f (x) y f (x) en x0 = 1
o
y0 = f (x0 ) = 15 − 105 + 180 = 148 (3.57)
m = f (x0 ) = 15 − 105 + 180 = 90 (3.58)
Por lo tanto la recta tangente que pasa por x = 1 ser´
a
y = y0 + m(x − x0 ) = 148 + 90(x − 1) = 90x + 58 (3.59)
3. (a) Para este ejercicio, debemos primero encontrar los puntos cr´
ıticos
de f (x). Para ello debemos derivar e igualar a cero.
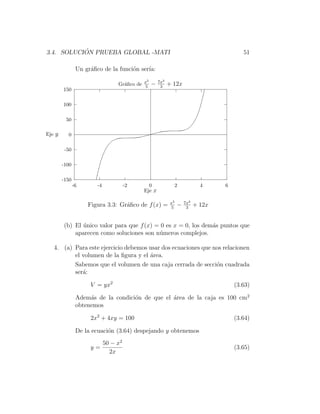
f (x) = x4 − 7x2 + 12 (3.60)
f (x) = 0 ⇒ x4 − 7x2 + 12 = 0
(x2 − 3)(x2 − 4) = 0 (3.61)
⇒ x2 − 3 = 0 ∧ x2 − 4 = 0
x2 = 3 x2 = 4
√
x=± 3 x = ±2 (3.62)
Ahora, debemos saber si la funci´n es creciente o decreciente. Para
o
ello usaremos los puntos cr´
ıticos, viendo si la primera derivada es
positiva o negativa.
En el intervalo (−∞, −2] ⇒ f (x) > 0 ⇒ f (x) es creciente
√
En el intervalo [−2, − 3] ⇒ f (x) < 0 ⇒ f (x) es decreciente
√ √
En el intervalo [− 3, 3] ⇒ f (x) > 0 ⇒ f (x) es creciente
√
En el intervalo [ 3, 2] ⇒ f (x) < 0 ⇒ f (x) es decreciente
En el intervalo [2, ∞) ⇒ f (x) > 0 ⇒ f (x) es creciente](https://image.slidesharecdn.com/librowilcken-120915205117-phpapp01/85/Librowilcken-50-320.jpg)


















































![102 CAP´
ITULO 4. SOLUCIONES DE LAS GU´
IAS
4.5 Soluci´n Gu´ 5
o ıa
1. Debemos encontrar el Area como funci´ de x. Para ello tenemos como
n
dato el per´
ımetro de un rect´ngulo que es
a
P = 2x + 2y = 200 (4.183)
x + y = 100
y = 100 − x (4.184)
Adem´s el ´rea de una rect´ngulo es A = x · y, reemplazando (4.184)
a a a
obtenemos
A(x) = x · y = x(100 − x) (4.185)
A(x) = 100x − x2 (4.186)
2. Como el lado de la pieza cuadrada es 16[cm2 ] si recortamos cuadrados
iguales de lado x de cada esquina podemos expresar el volumen en
funci´n de x.
o
V (x) = (16 − 2x)2 x (4.187)
= (256 − 64x + 4x2 )x
V (x) = 4x3 − 64x2 + 256x (4.188)
3. La ecuaci´n del c´
o ırculo es:
√
y = 16 − x2 (4.189)
Si tomamos como x la distancia entre el eje Y y la circunferencia.
Adem´s tomamos como y la distancia entre el eje X y la circunferencia
a
obtenemos que el ´rea ser´
a a
A √
= x · y = x 16 − x2 (4.190)
2](https://image.slidesharecdn.com/librowilcken-120915205117-phpapp01/85/Librowilcken-102-320.jpg)
![4.5. SOLUCION GU´ 5
´ IA 103
Por lo tanto el ´rea total de en funci´n de x ser´
a o a
√
A(x) = 2x 16 − x2 (4.191)
4. Sabemos que el ´rea A = 100[cm2 ]
a
Adem´s sabemos que
a
2x2 + 4xy = 200
x2 + 2xy = 100
2xy = 100 − x2
100 − x2
y = (4.192)
2x
Por otro lado sabemos que el volumen lo podemos expreasar como
V (x) = x2 · y (4.193)
100 − x2
V (x) = x2 (4.194)
2x
x
= (100 − x2 )
2
x3
= 50x − (4.195)
2
√
5. Dadas f (x) = 2x − 3 y g(x) = x + 1. Encontrar
(a) Dom(f ), Dom(g)
Dom(f ) = {x ∈ R} (4.196)
Dom(g) = {x ∈ R|x ≥ −1} (4.197)
(b) f + g
√
f (x) + g(x) = 2x − 3 + x+1 (4.198)
El dominio ser´ Dom(f + g) = {x ∈ R|x ≥ −1}
a
(c) f · g
√
f (x) · g(x) = x + 1(2x − 3) (4.199)
El dominio ser´ Dom(f · g) = {x ∈ R|x ≥ −1}
a](https://image.slidesharecdn.com/librowilcken-120915205117-phpapp01/85/Librowilcken-103-320.jpg)

![4.5. SOLUCION GU´ 5
´ IA 105
1
(d) f (x) = x−2 ,x > 0 g(x) = x− 2 x>0
f (x) = y = x−2
1
y = 2
x
yx2 = 1
1
x2 =
y
1
x = √
y
1
x = y − 2 = g(y) (4.206)
Por lo tanto g(y) = g(x), entonces las funciones son inversas una
de la otra.
1 1−x
(e) f (x) = x2 +1
g(x) = x
en ] 1 , 1[
2
1
f (x) = y =
x2 +1
1
(x2 + 1) =
y
1
x2 = −1
y
1−y
x2 =
y
1−y
x = = g(y) (4.207)
y
Por lo tanto hemos encontrado la inversa que adem´s es igual a la
a
entregada.
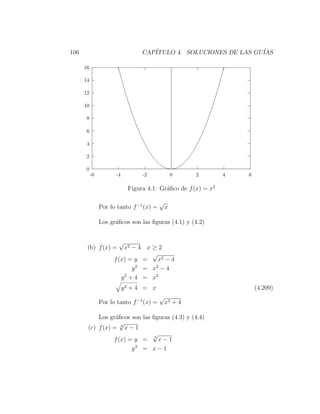
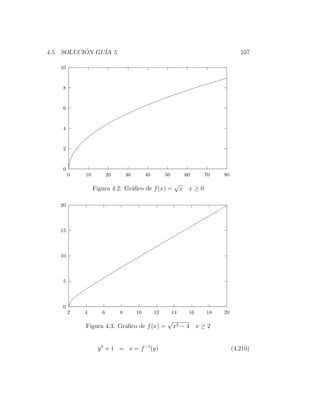
7. Encontrar la inversa y graficar f y f −1
(a) f (x) = x2 x≥0
f (x) = y = x2
√
2 = x = f −1 (y) (4.208)](https://image.slidesharecdn.com/librowilcken-120915205117-phpapp01/85/Librowilcken-105-320.jpg)







![4.6. SOLUCION GU´ 6
´ IA 119
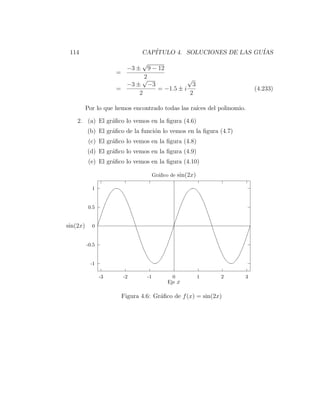
(a) sin(x) = 0
Debemos notar que sin(x) = 0 se cumple para x = 0, x = π,
x = 2π, etc.
Por lo tanto se cumple para todo x = kπ k = 0, 1, 2, . . .
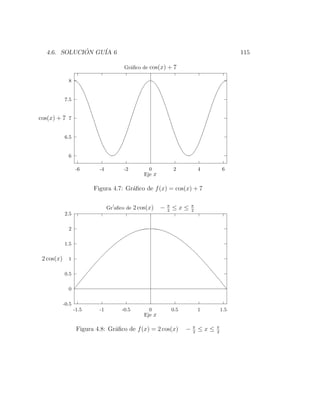
(b) cos(x) = 0
Vemos que cos(x) = 0 se cumple para x = π , x =
2
3π 5π
2
, 2, etc.
Por lo tanto se cumple para todo x = (2k + 1) π
2
k = 0, 1, 2, . . .
(c) sin(x) = −1
3π 5π
Vemos que sin(x) = −1 se cumple para x = 2
, 2, etc.
3π
Por lo tanto se cumple para todo x = 2
+ 2kπ k = 0, 1, 2, 3, . . .
(d) cos(x) = −1
Vemos que cos(x) = −1 se cumple para x = π, 2π, etc.
Por lo tanto se cumple para todo x = kπ k = 1, 2, 3, 4, . . .
7. Encontrar x en [0, 2π] para los que se cumple
1
(a) sin(x) = 2
Los valores son x = π , 5π
6 6
1
(b) cos(x) = √
2
Los valores son x = π , 3π
4 4
√
3
(c) sin(x) = 2
Los valores son x = π , 2π
3 3
1
(d) cos(x) = 2
Los valores son x = π , 5π
3 3](https://image.slidesharecdn.com/librowilcken-120915205117-phpapp01/85/Librowilcken-119-320.jpg)





























