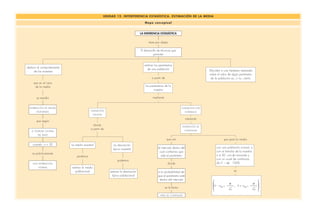
Este documento describe los conceptos básicos de la inferencia estadística, incluida la estimación de parámetros poblacionales como la media a partir de muestras. Explica que la media muestral se puede usar para estimar la media poblacional y que la desviación típica muestral se puede usar para estimar la desviación típica poblacional. También cubre la estimación por intervalos mediante intervalos de confianza, que son rangos dentro de los cuales se espera que se encuentre el parámetro con un cierto n

1. LA INFERENCIA ESTADÍSTICA
tiene por objeto
El desarrollo de técnicas que
permiten
deducir el comportamiento
de las muestras
UNIDAD 12. INTERFERENCIA ESTADÍSTICA. ESTIMACIÓN DE LA MEDIA
Mapa conceptual
que en el caso
de la media
se estudia
Dilucidar si una hipótesis realizada
sobre el valor de algún parámetro
de la población es, o no, cierta.
DISTRIBUCIÓN DE MEDIAS
MUESTRALES
que según
EL TEOREMA CENTRAL
DEL LÍMITE
cuando n > 30
es prácticamente
UNA DISTRIBUCIÓN
NORMAL
estimar los parámetros
de una población
a partir de
los parámetros de la
muestra
mediante
ESTIMACIÓN
PUNTUAL
donde
a partir de
La media muestral
podemos
estimar la media
poblacional
La desviación
típica muestral
podemos
estimar la desviación
típica poblacional
ESTIMACIÓN POR
INTERVALOS
mediante
ESTIMACIÓN DE
CONFIANZA
que son
el intervalo dentro del
cual confiamos que
esté el parámetro
donde
a la probabilidad de
que el parámetro esté
dentro del intervalo
se le llama
NIVEL DE CONFIANZA
que para la media
con una población normal, o
con el tamaño de la muestra
n ≥ 30, con σ conocida y
con un nuvel de confianza
de (1 – α) · 100%
es
(_
x + z α/2 σ )
x – z α/2 , _
√n
σ
√n