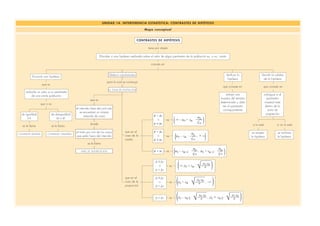
Este documento describe los contrastes de hipótesis, que consisten en verificar si una hipótesis planteada sobre el valor de un parámetro poblacional es cierta o no. Para ello, se enuncia una hipótesis sobre el valor de un parámetro, se extrae una muestra y se obtiene el valor del parámetro en la muestra. Luego, se compara el valor muestral con la zona de aceptación para decidir si se acepta o rechaza la hipótesis original. Los contrastes pueden ser bilaterales, unilaterales, sobre

1. UNIDAD 14. INTERFERENCIA ESTADÍSTICA: CONTRASTES DE HIPÓTESIS
Mapa conceptual
se le llama
que es
Dilucidar si una hipótesis realizada sobre el valor de algún parámetro de la población es, o no, cierta.
consiste en
Deducir conclusiones
para lo cual se construye
LA ZONA DE ACEPTACIÓN
Enunciar una hipótesis
atribuirle un valor a un parámetro
de una cierta población
que si es
de igualdad
(=)
CONTRASTE BILATERAL
de desigualdad
(≤ o ≥)
se le llama
CONTRASTE UNILATERAL
que es
el intervalo fuera del cual solo
se encuentran un número
reducido de casos
donde
al tanto por uno de los casos
que están fuera del intervalo
se le llama
NIVEL DE SIGNIFICACIÓN
que en el
caso de la
media
μ = μ0 (μ0 σ0
es – zα/2 · , √μ0 σ0
+ zα/2 · ) n
√n
μ > μ0
o
μ ≤ μ0
(–∞ μ0 σ0
es – + zα · ) √n
μ < μ0
o
μ ≥ μ0
σ0
es (μ0 – zα · , + ∞) √n
CONTRASTES DE HIPÓTESIS
tiene por objeto
(–∞ p0 + zα · √ ) p0 q0
(√ p0 q0
p0 + zα · , –∞ ) n
que en el
caso de la
proporción
p ≥ p0
o
p < p0
Verificar la
hipótesis
es
(√ p0 q0
p0 q0
) p0 – zα/2 · , p0 + zα/2 · √ n p = p0 es n
n
p ≤ p0
o
p > p0
es
que consiste en
extraer una
muestra del tamaño
determinado y obte-ner
el parámetro
correspondiente
Decidir la validez
de la hipótesis
que consiste en
averiguar si el
parámetro
muestral está
dentro de la
zona de
aceptación
si lo está
se acepta
la hipótesis
si no lo está
se rechaza
la hipótesis