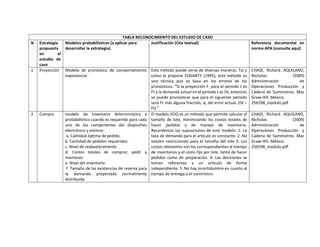
1. La presentación describe 6 estrategias propuestas en un estudio de caso y los modelos probabilísticos que podrían aplicarse para desarrollar cada estrategia, justificando la elección de cada modelo con citas textuales de referencias documentales. Se incluye también una bibliografía de 4 fuentes.

1. UNIDAD 1 Y 2: PASO 1 - DESARROLLAR Y PRESENTAR EL RECONOCIMIENTO DE LOS MÉTODOS
PROBABILÍSTICOS
PRESENTADO POR
MARTHA NAVARRETE
COD.1022959098
PRESENTADO A
ALVARO JAIR ROJAS BARACALDO
UNIVERSIDAD NACIONAL ABIERTA Y A DISTANCIA
MÉTODOS PROBABILÍSTICOS
29 AGOSTO 2018
BOGOTA

2. Reconocimiento de actores
1. Ingresar al perfil (nombre) y proceder a actualizar la información allí solicitada (datos e imagen)
e indicar el CEAD, CCAV, CERES o UDR al que pertenece y otros datos que considere de interés.
Actualizado el perfil de cada uno de los participantes del grupo de trabajo, ingresar a la etiqueta
Participantes, seleccionar uno a uno, el nombre de cada participante y tomar captura de
pantalla. Guardarlas como imagen.

3. Reconocimiento de los modelos probabilísticos
2. Diseñar un mapa conceptual con tema Métodos Probabilísticos, con base en los contenidos
temáticos del Syllabus del curso y fuentes documentales presentadas en la Unidad 1 - Técnicas
de pronósticos, teoría de Inventarios y toma de decisiones en sistemas de inventario y Unidad
2 - Cadenas de Markov, teoría de colas y programación no lineal, como estrategia de
pensamiento relacionado con la adquisición e integración del conocimiento, teniendo en
cuenta sus elementos: concepto, enlaces y proposiciones, estructura jerárquica (horizontal) y
una estructura categórica (vertical) y representación gráfica. Utilizar el programa Cmaptools y
guardar el mapa conceptual como imagen.

4. TABLA RECONOCIMIENTO DEL ESTUDIO DE CASO
N Estrategia
propuesta
en el
estudio de
caso
Modelos probabilísticos (a aplicar para
desarrollar la estrategia)
Justificación (Cita textual) Referencia documental en
norma APA (consulte aquí)
1 Proyección Modelo de pronóstico de comportamiento
exponencial
Este método puede verse de diversas maneras. Tal y
como la propone FOGARTY (1995), este método es
una técnica que se basa en los errores de los
pronósticos. “Si la proyección F, para el período t es
Ft y la demanda actual en el período t es Dt, entonces
se puede pronosticar que para el siguiente período
será Ft más alguna fracción, α, del error actual. (Dt –
Ft) “.
CHASE, Richard. AQUILANO,
Nicholas. (2009)
Administración de
Operaciones Producción y
Cadena de Suministros. Mac
Graw-Hill. México.
256598_modulo.pdf
2 Compra modelo de inventario determinístico y
probabilístico cuando es requerido para cada
uno de los componentes del dispositivo
electrónico y estimar:
a. Cantidad óptima de pedido.
b. Cantidad de pedidos requeridos.
c. Nivel de reabastecimiento.
d. Costos totales de comprar, pedir y
mantener.
e. Nivel del inventario.
f. Tamaño de las existencias de reserva para
la demanda proyectada normalmente
distribuida
El modelo EOQ es un método que permite calcular el
tamaño de lote, minimizando los costos totales de
hacer pedidos y de manejo de inventario.
Recordemos las suposiciones de este modelo: 1. La
tasa de demanda para el artículo es constante. 2. No
existen restricciones para el tamaño del lote 3. Los
costos relevantes son los correspondientes al manejo
de inventarios y el costo fijo por lote, tanto de hacer
pedidos como de preparación. 4. Las decisiones se
toman referentes a un artículo de forma
independiente. 5. No hay incertidumbre en cuanto al
tiempo de entrega o el suministro.
CHASE, Richard. AQUILANO,
Nicholas. (2009)
Administración de
Operaciones Producción y
Cadena de Suministros. Mac
Graw-Hill. México.
256598_modulo.pdf

5. 3 Decisión Modelo probabilístico de toma de decisiones
en sistemas de inventarios, evaluando:
a. Los cuatro distribuidores.
b. Tres distribuidores.
c. En futuro a TECOL S.A. como quinto
distribuidor.
Método de Holt – Winters. Este método de
pronóstico se basa en el método de suavización
exponencial, y se utiliza cuando la serie tiene una
marcada tendencia, así como un componente
estacional igualmente apreciable. El modelo tiene en
cuenta cuatro factores a saber: a) Componente
constante t S (se refiere por ejemplo al volumen de
ventas fijo que puede tener una empresa) b) El
componente de Tendencia Bt representa el ritmo
estructural de crecimiento o decrecimiento que
puede haber en las ventas. c) El componente
estacional Ct , representa el incremento y
decremento en el volumen de ventas en un período
de tiempo. d) Y un último elemento que siempre está
presente en todos los modelos de pronóstico y es el
error aleatorio que tiene este (e).
CHASE, Richard. AQUILANO,
Nicholas. (2009)
Administración de
Operaciones Producción y
Cadena de Suministros. Mac
Graw-Hill. México.
256598_modulo.pdf

6. 4 Participació
n
modelo de cadena Markov, para determinar:
a. Las probabilidades estacionarias de los
periodos futuros.
b. Las probabilidades de estado estable de la
participación.
Las cadenas de Markov se aplican en gran número de
situaciones, como son: los cambios de preferencia
que en el mercado tienen diferentes productos. La
posible decisión sobre hacer o no una inversión en
cierta oportunidad, etc., y el estado presente y los
estados futuros se representan por medio de
matrices.
Gallagher, C., & Watson, H.
(1982). Métodos
cuantitativos para la toma de
decisiones en
administración (pp. 331-
351), México, D.F., MX:
McGraw-Hill Interamericana.
Recuperado de:
http://bibliotecavirtual.unad
.edu.co:2077/lib
/unadsp/reader.action?docI
D=10479349&ppg=8.

7. 5 Servicio modelo de línea de espera bajo condiciones
de estado estable a. El diseño estadístico del
modelo de línea de espera.
1. Tiempos entre llegadas. 2. Tiempos de
servicio.
3. Determinar la tasa de llegada (λ) de
acuerdo a los tiempos entre llegadas, según
una Distribución de Exponencial o de Poisson.
4. Determinar la tasa de servicio (µ) de
acuerdo a los tiempos de servicio
5. Formular y plantear el modelo de Líneas
de Espera bajo condiciones de estado estable
(M/M/1): (DG/∞/∞).
6. Proponer gráficamente el diseño de la
instalación de servicio del modelo de línea de
espera.
7. Determinar las medidas de desempeño de
estado estable.
a. La probabilidad de inactividad en la
instalación de servicio.
b. La probabilidad de actividad al menos del
30%.
c. La probabilidad de actividad para el 20%.
d. La probabilidad de que un cliente tenga
que esperar.
e. La probabilidad de estar desocupado el
servidor.
f. La probabilidad de actividad de más del
25%. g. La probabilidad de que por lo menos
sean atendidos 10 clientes en una hora.
Esta es una herramienta determinista, esto es, se
supone que se conocen con certeza todos los
parámetros del modelo, lo que casi nunca sucede en
la vida real.Esta deficiencia se compensa con los
llamados análisis de sensibilidad,mediante los cuales
se van cambiando los datos o parametos y se
observan otras posibles soluciones del problema
Taibo, A. Investigación de
operaciones para los no
matemáticos (pp. 71-77),
México, D.F., MX: Instituto
Politécnico Nacional, 2009.
Accessed November 27,
2016. Recuperado
de:http://bibliotecavirtual.u
nad.edu.co:2077/lib/unadsp
/reader.action?docID=10504
970&ppg=8.

8. 6 Optimizaci
ón
un modelo de programación no lineal
estocástico para realizar una comparación
con la demanda proyectada
La Programación Estocástica reúne aquellos modelos
de optimización en donde uno o más parámetros del
problema son modelados a través de variables
aleatorias.
Una manera de enfrentar esta aleatoriedad consiste
en reemplazar los parámetros aleatorios por su valor
esperado, lo cual lleva a resolver un
problema determinístico de programación
matemática, los cuales son de especial interés en
cursos introductorios de Investigación de
Operaciones y donde la variabilidad inherente a los
parámetros se aborda a través del Análisis de
Sensibilidad o Postoptimal.
No obstante, la solución obtenida de esta manera
puede no ser representativa de la realidad, al no
considerar la dispersión de los valores que toman los
parámetros en torno al valor esperado, lo cual entre
otras cosas puede invalidar su implementación al
resultar finalmente escenarios muy diferentes del
promedio.
Taibo, A. Investigación de
operaciones para los no
matemáticos (pp. 71-77),
México, D.F., MX: Instituto
Politécnico Nacional, 2009.
Accessed November 27,
2016. Recuperado
de:http://bibliotecavirtual.u
nad.edu.co:2077/lib/unadsp
/reader.action?docID=10504
970&ppg=8.

9. BIBLIOGRAFIA
Amaya, A. J. (2009). Toma de decisiones gerenciales: métodos cuantitativos para la administración
(2a. Ed.) (pp. 47-57), Bogotá, CO: Ecoe Ediciones. Recuperado
de http://bibliotecavirtual.unad.edu.co:2077/lib/unadsp/reader.action?docID=10467109&ppg=9.
Ullmann, J. E. (1979). Métodos cuantitativos en administración: teoría y 512 problemas resueltos
(pp. 278-282), México, D.F., MX: McGraw-Hill Interamericana. Recuperado
de http://bibliotecavirtual.unad.edu.co:2077/lib/unadsp/reader.action?docID=10514989&ppg=6
Taibo, A. Investigación de operaciones para los no matemáticos (pp. 71-77), México, D.F., MX:
Instituto Politécnico Nacional, 2009. Accessed November 27, 2016. Recuperado
de:http://bibliotecavirtual.unad.edu.co:2077/lib/unadsp/reader.action?docID=10504970&ppg=8.
Gallagher, C., & Watson, H. (1982). Métodos cuantitativos para la toma de decisiones en
administración (pp. 331-351), México, D.F., MX: McGraw-Hill Interamericana. Recuperado
de:http://bibliotecavirtual.unad.edu.co:2077/lib/unadsp/reader.action?docID=10479349&ppg=8.