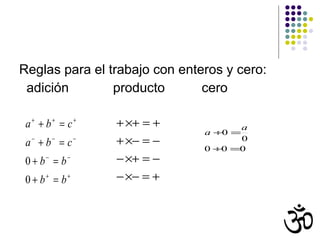
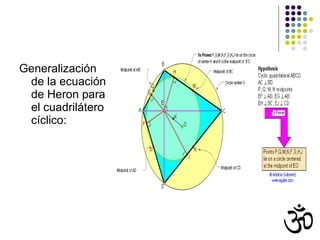
El documento resume la historia de las matemáticas en la antigua India. Explica que los hindúes desarrollaron un sistema de numeración decimal, incluyendo símbolos para los números del 0 al 9. También trabajaron con operaciones básicas, álgebra, geometría y trigonometría. Textos como los Sulbasutras y el Aryabhatiya contienen problemas y métodos matemáticos que anticipan conceptos modernos.

1. मतेमतिका इन्दु ख़ुवन कर्लोस रियञो

2. Contenido Orígenes de la cultura hindú. Sistema de numeración decimal. Operaciones básicas. Literatura matemática y sus autores

3. Orígenes de la civilización hindú Mohenjo-daro y Harappa (3.000 A.c.) en el valle del Indo. Contemporáneas de Egipto y Mesopotamia. Destruidas hacia el 1.300 A.c. Por los arios. Escribieron los vedas (Rig veda, Sama veda, Ayur veda y Atarva veda) periodo vedico. Implementaron el sistema de castas.

4. Sistema de numeración decimal Mohenjo-daro (palotes) Época Asoka (kharoshti) Brahmi Gwalior

5. Sistema de numeración decimal Periodo gupta Nagari

6. Código de escritura numérico Sunya (vacío)/ akasha (eter)/ ambara (atmosfera)/ viyat (cielo) 0 Buda 9 Serpiente/elefante/Krishna 8 Semana/ Krtika (osa mayor) / Rishis/ Rama 7 Pashurama 6 Sentidos/ mano/ vamana 5 Vedas/ mesa/ Narasimba 4 Fuego /árbol /cualidades /Varaha 3 Alas/ gemelos/ yami/yama/brazos/ kurma 2 Luna / sol (surya) / matsya 1 Palabra que sustituye al número Número

7. Ejemplo El numero 4´320.000 se lee como: 4 3 2 0 0 0 0 veda rama yama Sunya akasha ambara Viyat

8. Ventajas del sistema de numeración decimal Tiene una base decimal. Una notación posicional. Símbolos para los numerales básicos.

9. Conjuntos numéricos Naturales. 1234= 4321 Enteros. ° 4321 Fracciones Decimales

10. Además trabajaron las series numéricas, la mas conocida es la que aparece en la historia de Lahur Sessa, el legendario inventor del ajedrez. La serie es: 1, 2, 4, 8, 16, 32, 64, 128, ……………… Donde cada termino representa la cantidad de granos de arroz que el rey Iadava le habia prometido a Sessa por cada cuadro del tablero de ajedrez. Dicha promesa nunca pudo ser cumplida por que la cantidad de granos era de: 18´´´ 446. 744´´ 073. 709´ 551. 615 Cantidad que no se podría obtener sembrando solo arroz en toda la india durante 100 años.

11. Sunya (el vacío) La base fundamental de la cultura hindú es la religión. Dentro de ella el concepto de vacío es muy importante. Hacia el siglo VI aparece Siddharta Gautama (Buda) Enseño que las personas sufren por el deseo. Para liberarse debían abandonar toda condición particular. Así se debía llegar a un estado de vacuidad para unificarse con el todo (NIRVANA) El budismo fue muy influyente en la India, de allí que no es raro que después fuera inventado un símbolo numérico para el vacío.

12. ¿Sabían que noventa y cinco sumado con cinco da como resultado 46?

13. Operaciones básicas Suma: es igual que como la usamos actualmente. Ej.: Tatra tiene (buda, mano) dinares y su amigo Bhata le paga (sentidos) ¿Cuánto tiene Tatra? पा 46 95 5 ज ु

14. Resta: charya tiene (buda, brazos, luna) dinares y paga (Krishna, sol) ¿Cuánto le queda? पा 471 921 81 +

15. Con enteros: Mumba le debe (buda, vamana) dinares a su amigo akrya, si le paga (mano) ¿Cuánto queda debiendo ? ° पा 45 ° 95 5 ज

16. Aryabhata fue el primer matemático en sumar y restar fracciones usando mínimo común múltiplo, tal como se hace hoy en día: Sumar 3/5 con 2/4 3 2 Yu 5 4 Mcm (5,4) = 20 y amplificando fracciones se obtiene: 12 10 Yu pha 22 20 20 20

17. Multiplicación De números compuestos por dos dígitos. Gomutrika (trayectoria de la orina de la vaca) Gelosia (llamada así por los europeos, debido a su parecido con las rejillas de madera de las iglesias entre los siglos XIV y XV en Italia)

18. De números compuestos por dos dígitos. Primero se hace 2x7 y se escribe debajo. Luego 4x3. Después se multiplica en x y los resultados se colocan debajo. Se suman los resultados y solo hay que llevar cuando se hace la suma.

19. Gomutrika (Brahmagupta) Multiplicar 235 por 264. 2 235 6 235 4 235 _________ 470 1410 940 __________ 62040

20. Gelosia Los matemáticos hindúes a partir del siglo V, efectuaron la multiplicación por el procedimiento conocido con el nombre de “cuadrículas”. Ej. multiplicar Multiplicar 6 358 por 547 Es llamada erróneamente multiplicación musulmán.

21. 6 5 3 8 5 6 538 por 547 4 7

22. 6 5 3 8 7 4 5

23. 6 5 3 8 7 4 5 4 2

24. 6 5 3 8 7 4 5 4 2 5 3 1 2 6 5 4 2 0 2 2 1 2 3 0 3 5 1 5 2 0 4

25. 6 5 3 8 7 4 5 4 2 5 3 1 2 6 5 4 2 0 2 2 1 2 3 0 3 5 1 5 2 0 4 6 7 5 3 6 8 2

26. 6 5 3 8 7 4 5 4 2 5 3 1 2 6 7 5 3 6 8 2 6 5 4 2 0 2 2 1 2 3 0 3 5 2 5 1 0 4 El resultado se lee de izquierda a derecha así: 6538 x 547 = 3 5 7 6 2 8 6

27. Por ejemplo: multiplicar 537 por 24 Para lo cual construimos la cuadrícula siguiente:

28. 5 3 7 2 4

29. 5 3 7 2 4

30. 5 3 7 2 4 1 0 2 4 1 6 0 8 2 2 1 0

31. 5 3 7 2 4 1 0 2 4 1 6 0 8 2 2 1 0 1 2 8 8 8

32. 5 3 7 2 4 1 0 2 4 1 6 0 8 2 2 1 0 1 2 8 8 8 Luego 537 x 24 = 12 888

33. Con fracciones: el manuscrito Bhaskshali muestra operaciones con fracciones como las siguientes:

34. División (galera) Método para dividir similar al que usamos hoy en día. Llega a occidente gracias al contacto de los europeos con los árabes (cruzadas)

35. Dividir 44.977 entre 382 (por el método moderno y por galera. 44977 382 382 117 677 382 2957 2674 283

36. 382 44977

37. 67 382 44977 1 382

38. 29 675 382 44977 11 3822 38

39. 28 293 675 382 44977 117 38224 387 26

40. Con fracciones: en el manuscrito Bhaskshali se muestra de la siguiente forma: Donde el símbolo बा es bha o parte

41. Radicación El manuscrito Bhaskshali muestra una formula para hallar las raíces cuadradas de números que no son cuadrados perfectos. Donde x es el numero a radicar, y n el cuadrado anterior mas cercano P ej. Encontrar la raíz de 10,5 X= 10,5 n = 3 por que 3x3 = 9

42. Matemáticos y literatura matemática. La escritura vedica es principalmente religiosa y ceremonial. Los vedantas están compuestos en seis partes, las dos ultimas son de astronomía y rituales. Dentro de los rituales se encuentran los sulbasutras.

43. Sulbasutras (reglas de la cuerda) Son textos que indicaban las reglas y procedimientos en la construcción de altares. La perfección de los altares les daría el favor de los dioses. No contienen demostraciones, solo reglas. Baudhayana (800 AC) Manava (750 (200 AC) Apastamba (600 AC) Katyayana (200 AC)

44. Teorema de Pitágoras Katyayana: la soga que se tiende sobre la diagonal de un rectángulo, produce un área que es la que dan los lados vertical y horizontal.

45. Apastamba: indica la construcción de altares trapezoidales, con el uso de ternas pitagóricas

46. Baudhayana: aparentemente emplea la rotación de figuras (Euclides) para el teorema de Pitágoras.

47. Además en los sulbasutras aparece una forma para el teorema de Pitágoras por comparación de lados.

48. Cuadratura del circulo y raíz de dos En los sulbasutras aparece el método conocido como 13/15 para la cuadratura del circulo. Katyayana hace una aproximación de raíz de dos: añade a la unidad de longitud su tercera parte y a esta tercera parte su propia cuarta parte menos la trigésimo cuarta parte de ese cuarto.

49. Siddhantas (sistemas astronómicos) Fueron escritos en el periodo Gupta ( 290 d.c) Paulisha. Surya (sol) Vasisishta. Paitamaha. Romanka. Expresan el valor de Π : 3 177/1250 que coincide con el valor sexagesimal 3; 8,30 que había dado claudio Ptolomeo. Por primera vez en la historia, el Surya Siddhanta emplea la semicuerda para la función trigonométrica seno ख़िबा (jiva) ओत्क्रम ख़िबा (otkram jiva) कोख़िबा (kojiva)

50. De la distancia meridiana del zenit del sol encuentre jiva (seno base) y kojiva (coseno o seno perpendicular), si entonces el radio se multiplicara por la medida del gnomon en dígitos y dividido por el kojiva, los resultados son la sombra del gnomon y la hipotenusa al medio día. G=medida del gnomon. R= radio del gnomon. S=sombra del gnomon. H= hipotenusa del gnomon

51. Manuscrito Bhaskshali Anterior al siglo v D.c. Encontrado cerca a la villa del mismo nombre en 1881. Contiene: Operaciones básicas. Solución de ecuaciones. Sistemas de ecuaciones. Regla de tres.

52. Plantea ecuaciones donde la incógnita se escribe de manera similar al símbolo para sunya.

53. Muestra soluciones a problemas, que hoy en día resolvemos con sistemas de tres ecuaciones: Ej. Una persona posee siete caballos “Asava”, otro nueve caballos “Haya” y otro diez camellos. Cada uno da dos animales, uno a cada persona. Quedando los tres con el mismo valor monetario. Encuentre el valor de cada animal y el valor total de todos los animales

54. Para solucionar el problema, primero decimos Que: valor del caballo Asava. valor del caballo Haya. valor del camello.

55. Se plantea la igualdad: Donde k es el el valor total de los animales. Después se estos se reparten como lo plantea el enunciado: (1) Luego se quitan los animales que acabamos de repartir y sustraemos a cada parte de la igualdad un animal. (2)

56. La igualdad queda de la siguiente forma (3) El valor de es 168 ya que es valor de multiplicar los tres coeficientes resultantes 6x4x7=168 Lo que se hace es igualar cada parte de la igualdad con 168.

57. Esto se hace de la siguiente forma

58. Los valores se sustituyen en (3) Como es una igualdad:

59. También usaban la regla de tres para solucionar problemas del tipo: si un hombre gana 50 dinares en ocho días ¿Cuánto ganara en doce? 8 = pramana 50 = phala 12 = iccha La regla es: phala x pramana / iccha (50 x 12) / 8 = 75 dinares

60. Aryabhatiya (Aryabhata- siglo VI DC) Escribió 33 versos sobre: Calculo de raíces. Geometría. Aritmética. Trigonometría esférica. Tablas de senos: sen30°= ½ Notación del sistema de numeración decimal.

61. En el Aryabhatiya: hay una regla para el calculo de pi.: chaturadhikam śatamaśṭaguṇam dvāśaśṭistathā sahasrāṇām Ayutadvayaviśkambhasyāsanno vrîttapariṇahaḥ. Esto quiere decir: suma 4 a 100, multiplica por 8 y súmale 62000. el resultado te da aproximadamente la circunferencia de un circulo cuyo diámetro es de 20000

62. También contiene reglas para calcular la suma de términos de una progresión:

63. Usa un lenguaje muy florido para solucionar la cuarta proporcional a tres números dados: En la regla de tres multiplica el fruto por el deseo y divide por la medida: el resultado será el fruto del deseo: Donde a es la medida, b el fruto, c el deseo y x el fruto del deseo

64. Brahmasphutasiddanta(el sistema del universo por Brahmagupta) Texto de astronomía y matemáticas. Reglas para el trabajo con enteros y cero. Generalización de la formula de Heron de Alejandría. Finalizo el proceso que diera origen al sistema de numeración decimal. Planteo ternas pitagóricas.

65. Reglas para el trabajo con enteros y cero: adición producto cero

66. Generalización de la ecuación de Heron para el cuadrilátero cíclico:

67. Ternas pitagóricas: trabajo las ternas bajo la forma: Junto con las formulas para las diagonales:

68. El Lilavati y vijaganita (De Bhaskaracharya) Reglas para la división por cero. Calculo para el área del circulo (cuadratura) Dio soluciones a la ecuación de Pell

69. Regla para la división por cero: dividiendo 3, divisor 0, cociente la fracción 3/0. esta fracción de la que el denominador es cifra se llama cantidad infinita. En esta cantidad que consiste en lo que tiene cifra como divisor no hay alteración posible, por mucho que se añada o se extraiga, lo mismo que no hay cambio en Brahma infinito e inmutable. También afirmo que a/0 x 0 = a

70. Calculo el área del circulo, dividiendo este en sectores iguales, y rectificando las semicircunferencias. El área del circulo será igual al producto de la semicircunferencia por la altura del circulo.

71. Da soluciones particulares a la ecuación diofantica (conocida como ecuación de Pell) "Dime, OH matemático, ¿cuál es el cuadrado que multiplicado por 8 se convierte - junto con la unidad - en un cuadrado?" Que tiene la solución X =1 y = 3 o también (x,y)= (1,3)

72. Jyasthadeva y Mahajivanayama prakara Escritos por Madhava de Sangamagramma conocido como Golavid (maestro de las esferas) Trabajo series infinitas que luego fueron descubiertas siglos mas tarde en Europa. Sus trabajos llegan a nosotros por medio de sus aprendices Nilakantha Somayaji y Jyesthadeva.

73. Trabajo el calculo y la prueba de la serie de potencias para la tangente inversa: El primer termino es el producto de la condición y dado el radio del arco dividido por el coseno del arco. El éxito se obtiene por el cuadrado de la condición y divido por el cuadrado del coseno. Todos los términos se dividen por el numero impar 1,3,5,… el arco se obtiene sumando y restando respectivamente los términos de rango impar, inclusive los de rango. Se establece que la condición del arco o la de su complemento que es el menor debe ser tomado aquí como condición dada. De otro modo los términos obtenidos por encima de esta iteración no tienden a desaparecer la magnitud.

74. Esto es : Esta serie se conoce como serie de Gregory (fue descubierta por James Gregory 300 años después) hoy se denomina como serie de Madhava-Gregory

75. En el Mahajivanayama prakara dicta la serie que conocemos hoy como serie de Leibniz-Madhava. Además dio tres formas de Rn que mejoran la aproximación:

76. Además redacto una serie en verso para el valor de pi.: Dioses(33), ojos(2), elefantes(8), serpientes (8), fuego (3), cualidades (3), vedas(4), naksatras (27), elefantes (8) y brazos ( 2); el sabio dice que esta es la medida de la circunferencia cuando el diámetro del circulo es de 900.000.000.000.

77. Conclusiones. Los aportes mas importantes de la matemática hindú fueron: El sistema decimal de numeración que simplifico el trabajo en las matemáticas alrededor del mundo. Los algoritmos que hoy en día utilizamos para realizar las operaciones básicas. La notación para las funciones trigonometrícas seno y coseno.

78. Bibliografía: Boyer Carl B. historia de la matemática, alianza editorial, Madrid España 2003. http:// paraisomat.ii.uned.es / paraiso / historia.php?id = in_mate www.uhu.es/candido.pineiro/historia/india.pdf www.librosmaravillosos.com/hombrecalculaba/capitulo18.html - 32k - www.mat.uson.mx/depto/publicaciones/apuntes/pdf/2-1-1-india.pdf http://ciencia.astroseti.org/matematicas

79. शुक्रिजा