Este plan de clase describe las lecciones sobre números enteros, racionales fraccionarios y decimales. Se enseñarán las características y propiedades de estos números a través de ejemplos y demostraciones. Los estudiantes aprenderán a leer, escribir y aplicar estos números en situaciones cotidianas mediante ejercicios y problemas. El progreso de los estudiantes se evaluará con pruebas escritas y cuestionarios.








![PLAN DE CLASE
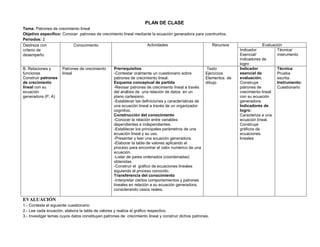
Tema: Leyes y propiedades de los números enteros, racionales fraccionarios y decimales.
Objetivo específico: Conocer las diferentes leyes y propiedades de los números enteros y racionales a través de los procesos de demostración para
aplicarlos en la resolución de problemas y ejercicios
Periodos: 3
Destreza con
criterio de
desempeño
Actividades Recursos Evaluación
Indicador Esencial/ indicadores de
logro
Técnica/
instrumento
B. Numérico
Deducir las
leyes y
propiedades
que rigen las
operaciones
básicas en
relación con
los números
enteros y
racionales.
Ciclo del Aprendizaje
Experiencia
- Elaborar una lluvia de ideas para recordar las
leyes que rigen a los conjuntos numéricos.
Reflexión
-Presentar y leer un ejercicio combinado con
números enteros y racionales.
-Identificar las operaciones a resolver y las
propiedades o leyes que pueden aplicarse para su
resolución. Uso de los signos de agrupación.
Conceptualización
- Explicar el proceso de resolución de cada
operación.
-Homologar los procesos y propiedades de
números enteros a racionales fraccionarios y
decimales.
Aplicación
-Escribir el contenido de las diferentes reglas y
propiedades conocidas.
-Ejemplificar leyes y propiedades.
Texto, tarjetas
memorias.
Indicador esencial de evaluación.
Deduce leyes y propiedades de las
operaciones básicas
Indicadores de logro:
-Deduce y aplica leyes matemáticas.
Suprime signos de agrupación.
Técnica: Prueba
escrita.
Instrumento:
Ejercicios
EVALUACIÓN
1.- Explica el contenido de las siguientes propiedades y escribe un ejemplo: Asociativa, distributiva de la multiplicación con respecto a la suma y a la resta,
cancelativa, modulativa de la suma, modulativa de la multiplicación, distributiva de la división.
2.- Resuelve los siguientes ejercicios suprimiendo los signos de agrupación y reduciendo expresiones numéricas.
{ 15 + 3 ( 8-2) -6}
[ -2 ( 12 +3-4) : 16 +5 (7-129 ]
¾ +⅔ ( 7 + 2) - ( ⅝ -½ ) =](https://image.slidesharecdn.com/plandeclasesmatematicas8-9-10-150318194308-conversion-gate01/85/Plan-de-clases-matematicas-8-9-10-10-320.jpg)
![PLAN DE CLASE
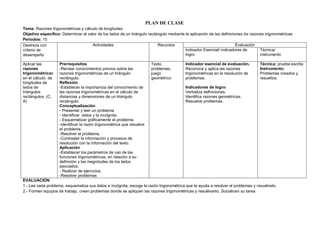
Tema: Expresiones con números enteros racionales, racionales fraccionarios y decimales positivos.
Objetivo específico: Conocer las diferentes leyes y propiedades de los números enteros y racionales a través de los procesos de demostración para
aplicarlos en la resolución de problemas y ejercicios
Periodos: 6
Destreza con
criterio de
desempeño
Actividades Recursos Evaluación
Indicador Esencial/ indicadores de
logro
Técnica/
instrumento
B. Numérico
Simplificar
expresiones
con números
enteros,
racionales
fraccionarios
y decimales
positivos con
la aplicación
de las
operaciones
básicas (P,A)
Prerrequisitos
-Resumir las diferentes leyes y propiedades de las
cuatro operaciones básicas.
Esquema conceptual de partida
-Presentar y analizar una expresión con números
enteros, racionales fraccionarios y decimales.
Construcción del conocimiento
-Identificar los bloques considerando los signos de
agrupación y la jerarquización de las operaciones.
-Deducción de los procedimientos para reducción
de expresiones numéricas.
-Ejemplificación sobre el uso de las cuatro
operaciones básicas y sus propiedades, en forma
gradual.
Transferencia del conocimiento
-Realización de actividades asociadas a la
simplificación de expresiones numéricas como la
resolución de problemas que se presentan en la
vida cotidiana.
Ejercicios, texto Indicador esencial de evaluación.
Simplifica expresiones con números
enteros, racionales fraccionarios y
decimales con el uso de las
operaciones básicas
Indicadores de logro:
-Suprime signos de agrupación.
-Reduce expresiones numéricas.
-Resuelve operaciones básicas
Técnica: Prueba
escrita.
Instrumento: Ejercicios
y problemas
EVALUACIÓN
1.- Resuelve los siguientes ejercicios suprimiendo los signos de agrupación y reduciendo expresiones numéricas.
{ 12 -5 (1/2 + 2/3) : 6 – 2 (0.5 + 0.3 – 1.2) } =
12/5 . 15/9 : ¼ + 3/8 =
2 [ 12- 4 : 3/8 ] + ( 2.5 – 3.2) =
2.- Elabora y resuelve problemas aplicados a tu realidad.](https://image.slidesharecdn.com/plandeclasesmatematicas8-9-10-150318194308-conversion-gate01/85/Plan-de-clases-matematicas-8-9-10-11-320.jpg)




![PLAN DE CLASE
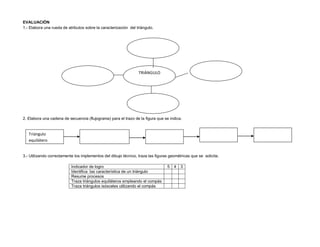
Tema: Cuatro operaciones de forma independiente con números racionales
Objetivo específico: Deducir los diferentes postulados de la congruencia de triángulos a través de la medición directa de lados y ángulos para la resolución
de problemas.
Periodos: 6
Destreza con
criterio de
desempeño
Actividades Recursos Evaluación
Indicador Esencial/ indicadores de logro Técnica/
instrumento
B. NUMÉRICO
Resolver las
cuatro
operaciones
de forma
independiente
con números
enteros,
racionales ,
fraccionarios y
decimales
(C,P)
Resolución de Problemas
-Presentar y leer un problema.
-Identificar los datos y la pregunta.
-Plantear la ecuación matemática que resuelve el
problema.
-Indicar el proceso de resolución.
-Escribir la respuesta.
-Comparar la respuesta con la pregunta.
-Analizar retrospectivamente el proceso.
-Realizar otras ejemplificaciones considerando
números racionales fraccionarios y decimales .
-Resolver ejercicios asociados a las cuatro
operaciones, de forma independiente primero con
números enteros, luego con decimales y por último
con fracciones
- Ejecutar ejercicios de las cuatro operaciones
básicas combinando los diferentes conjuntos de
números.
-Realización de actividades asociadas a la
resolución de las cuatro operaciones básicas en
problemas reales.
Ejercicios,
problemas, texto
Indicador esencial de evaluación
Opera con las cuatro operaciones básica
de forma independiente, usando el conjunto
numérico.
Indicadores de logro:
Define propiedades.
Aplica propiedades.
Resuelve ejercicios.
Crea y resuelve problemas
Técnica: Prueba
escrita.
Instrumento:
cuestionario,
ejercicios, escala
numérica
EVALUACIÓN
1.- Contesta:
a) ¿Qué operaciones tienen la propiedad asociativa?, b) ¿A qué llamamos inverso aditivo, inverso multiplicativo?, c) ¿Cuál es el orden de resolución de las
operaciones?
2.- Resuelve los siguientes ejercicios: 154 – ( 1/3 + 4/5 ) + [9 (0.5 + 1,2] = 2/5 : 1/3 + 3/5 ( 2 – 3/8)
3.-Lee, razona y resuelve los siguientes problemas.
a) Se vende la mitad de una hacienda de 150 ha. La tercera parte del resto se siembra de caña de azúcar y lo que sobra se divide para tres personas. ¿Qué
extensión recibe cada una?](https://image.slidesharecdn.com/plandeclasesmatematicas8-9-10-150318194308-conversion-gate01/85/Plan-de-clases-matematicas-8-9-10-16-320.jpg)





![EVALUACIÓN:
1.- Lee cada conjunto de operaciones e indica el orden de resolución.
8 ( -5) + 4 {-20 : (5) + 9(-2) + 10 = - { -6 [-12 : 6 + (-4) (-2) ] – 10 (0) =
2.- Resuelve los ejercicios anteriores
3.- Resuelve los siguientes ejercicios y problemas aplicando las leyes y propiedades de la jerarquización de operaciones.
(25) (-36) + 105 : 7 – (24 – 6) + (-8)(-2) = -5 (4+12) : (40 : 5) + (7 -10) =
a) El producto de las cifras de un número de tres cifras es 64. Si la cifra de las unidades es el doble de las decenas y éste el doble de las centenas, ¡cuál es
el número?
b) Si el producto es 114 808 y uno de los factores es 254, ¡cuál es el otro factor?
PARA NÚMEROS RACIONALES
2/3 (3/5 – 6/2) – (1/4 +3/2) : 7/3 = (1/3 -1/4 +2/5) 0.5 (0.5- 2 1/3) (2/7 – 3/7)=
Un señor tiene $ 5 600. Si en la mañana gasta 3/8 del dinero y en la tarde gasta 1/5 de lo que le queda, calcula el dinero que le sobra al señor.
De una varilla de hierro, Juan toma los 3/15, José los 2/7 y Rolando los 2/5. Si sobran los 36 cm, ¿cuánto midió la varilla?](https://image.slidesharecdn.com/plandeclasesmatematicas8-9-10-150318194308-conversion-gate01/85/Plan-de-clases-matematicas-8-9-10-22-320.jpg)
![EVALUACIÓN QUIMESTRAL
1.- D.C.D. Resolver las cuatro operaciones de forma independiente con números enteros, racionales , fraccionarios y decimales (C,P)
8 ( -5) + 4 {-20 : (5) + 9(-2) + 10} = - { -6 [-12 : 6 + (-4) (-2) ] – 10 (0) } =
2.-D.C.D. Definir y representar medianas, mediatrices alturas y bisectrices de un triángulo en gráficos.
En cada gráfico traza la línea que se indica
Medianas mediatriz altura bisectriz
3.- D.C.D. Determinar el baricentro , ortocentro, incentro y circuncentro de un triángulo en gráficos.
Traza triángulos y encuentra el: baricentro, ortocentro y circuncentro.
3.- Reconocer y representar monomios homogéneos
Representa gráficamente los siguientes monomios homogéneos: 3 abc 2X² Y 4XY²
4.- D.C.D. Resolver operaciones combinadas de adición, sustracción multiplicación y división exacta con números enteros, racionales, fraccionarios y
decimales.
{1/2 – 3 + 5/2 + 1/4} 2 – 3 + (1/2 – 1/3) 3( 5 -3/4) : (7-4 ) + (1/2 – ¾) 4 + 3/5 -0,5 : 2 (8-5)](https://image.slidesharecdn.com/plandeclasesmatematicas8-9-10-150318194308-conversion-gate01/85/Plan-de-clases-matematicas-8-9-10-23-320.jpg)


















![PLAN DE CLASE
Tema: Expresiones de números reales
Objetivo específico: Simplificar expresiones con números reales a través de la aplicación de las de propiedades y algoritmos matemáticos conocidos
Periodos: 8
Destreza con
criterio de
desempeño
Actividades Recursos Evaluación
Indicador Esencial/ indicadores de
logro
Técnica/
instrumento
Simplificar
expresiones
de números
reales con la
aplicación de
las
operaciones
Básicas (P, A)
Prerrequisitos
-Resolver operaciones con números reales
mediante un dominó.
Esquema conceptual de partida
-Presentar y leer una expresión de números
enteros.
-Determinar el orden de resolución de las
operaciones.
Construcción del conocimiento
-Aplicar las reglas de las operaciones básicas, para
desarrollar de forma gradual y ordenada ( suma,
resta, multiplicación, división), con el uso de signos
de agrupación.
-Ejemplificar la simplificación de expresiones con
números reales.
Transferencia del conocimiento
-Ejecución de actividades (ejercicios) que
impliquen la simplificación .de expresiones con
operaciones básicas.
Texto
Ejercicios
Indicador esencial de evaluación.
Simplifica expresiones de números
reales aplicando operaciones básicas.
Indicadores de logro:
Conoce y aplica propiedades.
Jerarquiza la resolución de
operaciones básicas.
Resuelve operaciones básicas.
Simplifica expresiones numéricas
Técnica: Prueba
escrita.
Instrumento: Ejercicios
EVALUACIÓN
1.- Simplifica las siguientes expresiones con números reales:
( ½ + ¾) - [ 6 + ( 0.5 -1.3) : 1/2] =
-6 - { 2 - [ ¾ : 6/9] + ( -3) ( 1/6) -10} =](https://image.slidesharecdn.com/plandeclasesmatematicas8-9-10-150318194308-conversion-gate01/85/Plan-de-clases-matematicas-8-9-10-42-320.jpg)

![PLAN DE CLASE
Tema: Operaciones combinadas de adición, sustracción, multiplicación y división exacta
Objetivo específico: Resolver ejercicios con operaciones combinadas a través de la aplicación de los distintos algoritmos matemáticos para desarrollar el
pensamiento lógico – matemático.
Periodos: 6
Destreza con
criterio de
desempeño
Actividades Recursos Evaluación
Indicador Esencial/ indicadores de
logro
Técnica/
instrumento
B. Numérico
Resolver
operaciones
combinadas
de adición,
sustracción,
multiplicación
y división
exacta con
números
racionales (P,A)
Experiencia
-Recordar los procesos de operaciones con
números enteros y fraccionarios resolviendo
ejercicios independientes.
Reflexión
-Elaborar de un cuadro resumen de las
propiedades de las operaciones con números
racionales (decimales y fracciones)
-Establecer los procedimientos de desarrollo en la
resolución de operaciones combinadas
(jerarquización), destrucción de signos de
agrupación.
Conceptualización
-Ejemplificar el proceso de resolución de
operaciones combinadas. (en forma graduada)
-Analizar retrospectivamente los procesos
aplicados.
Aplicación
-Resolver ejercicios de fijación, refuerzo y
aplicación de las operaciones combinadas de
adición , sustracción, multiplicación y división con
números racionales
Texto
Ejercicios
Indicador esencial de evaluación.
Resuelve operaciones combinadas
con números racionales.
Indicadores de logro:
Jerarquiza la resolución de
operaciones.
Reconoce y aplica diferentes
algoritmos matemáticos.
Resuelve operaciones
Técnica: Prueba
escrita.
Instrumento:
Ejercicios combinados
NOTA: Igual proceso para expresiones con números irracionales.
EVALUACIÓN
1.- Elabora flujogramas o cadenas de secuencia para resumir los procesos de resolución de las diferentes operaciones con números racionales.
2.- Lee cada ejercicio, identifica las operaciones a resolver, recuerda los procesos de resolución y aplícalos.
[3/5 + ( - 8/3) ] + 7/3 : (3/8 : 9/ 16) =](https://image.slidesharecdn.com/plandeclasesmatematicas8-9-10-150318194308-conversion-gate01/85/Plan-de-clases-matematicas-8-9-10-44-320.jpg)
![PLAN DE CLASE
Tema: Reglas y propiedades de la potenciación
Objetivo específico: Conocer las propiedades de la potenciación con números racionales mediante la demostración para resolver ejercicios
Periodos: 2
Destreza con
criterio de
desempeño
Actividades Recursos Evaluación
Indicador Esencial/ indicadores de
logro
Técnica/
instrumento
Aplicar las
reglas y
propiedades
de la
potenciación
con números
racionales
Prerrequisitos
- Elaborar un organizador gráfico sobre lo que
conocen de la potenciación con números enteros.
Esquema conceptual de partida
-Contestar oralmente un cuestionario: cuáles son
las propiedades de la potenciación, qué significa el
exponente negativo y cómo se convierte en
positivo,
Construcción del conocimiento
-Demostrar las propiedades descritas
anteriormente.
-Aplicar las propiedades de la potenciación en la
resolución de ejercicios.
Transferencia del conocimiento
-Resolución de ejercicios con potenciación.
Texto
Ficha de
memoria
ejercicios
Indicador esencial de evaluación.
Simplifica expresiones de números
racionales aplicando las reglas de
potenciación y radicación.
Indicadores de logro:
Deduce reglas.
Aplica reglas.
.
Técnica: Prueba escrita
Instrumento:
Cuestionario
NOTA: Igual proceso para las reglas y propiedades de la radicación.
EVALUACIÓN
1.- Completa correctamente las siguientes proposiciones.
a) Para resolver miltiplicaciones de igual base debemos …………………. los exponentes.
b) Todo número elevado al exponente cero tiene como potencia ……………………
c) La potenciación es distributiva con respecto a la ……………………….. y a la ………………………..
2.- Escribe las potencias correspondientes
( -5 )³=
(3/4) ²=
(-2) (-2²) (-2)½ (-2)³ =
( 15 : 5 )³ =
[ ( -2)² ]³ =](https://image.slidesharecdn.com/plandeclasesmatematicas8-9-10-150318194308-conversion-gate01/85/Plan-de-clases-matematicas-8-9-10-45-320.jpg)
![PLAN DE CLASE
Tema: Expresiones de números reales
Objetivo específico: Conocer las propiedades de la potenciación y radicación a través de la deducción para resolver ejercicios de simplificación.
Periodos: 6
Destreza con
criterio de
desempeño
Actividades Recursos Evaluación
Indicador Esencial/ indicadores de
logro
Técnica/
instrumento
Simplificar
expresiones
de números
racionales con
la aplicación de
las reglas de
potenciación y
de radicación
(P,A)
Prerrequisitos
-Elaborar un organizador gráfico sobre las
propiedades de la potenciación y radicación de
números enteros a través de un cuadro
comparativo.
Esquema conceptual de partida
-Presentar y analizar un ejercicio de simplificación
de expresiones de números racionales.
-Señalar las operaciones a resolver considerando
su jerarquía y signos de agrupación.
Construcción del conocimiento
-Resolver el ejercicio presentado.
-Contrastar los procesos aplicados con la
información del texto.
Transferencia del conocimiento
-Resolver ejercicios con operaciones que incluyan
potenciación y radicación.
Texto
Ficha de
memoria
ejercicios
Indicador esencial de evaluación.
Simplifica expresiones de números
racionales aplicando las reglas de
potenciación y radicación.
Indicadores de logro:
Deduce reglas.
Aplica reglas.
Simplifica expresiones.
.
Técnica: Prueba
escrita
Instrumento:
Cuestionario
EVALUACIÓN
1.- Indica el orden jerárquico de las operaciones en una expresión matemática.
2.- Lee cada ejercicio, identifica las operaciones a resolver, recuerda los procesos de resolución y aplícalos
(-2) (-2)² + [ ½ - 3 ( 2 + ¼)²] =
{ -4 : (5 – 3)² - ( ¾ + 2 ): 2/3 )³ -10}=
√ 25 : (3+2) - (2/5)³ + ( 5 -3 +10 – 7) =](https://image.slidesharecdn.com/plandeclasesmatematicas8-9-10-150318194308-conversion-gate01/85/Plan-de-clases-matematicas-8-9-10-46-320.jpg)
![PLAN DE CLASE
Tema: Expresiones de números reales con exponentes negativos
Objetivo específico: Conocer las propiedades de la potenciación y radicación a través de la deducción para resolver ejercicios de simplificación
Periodos: 4
Destreza con
criterio de
desempeño
Actividades Recursos Evaluación
Indicador Esencial/ indicadores de
logro
Técnica/
instrumento
Simplificar
expresiones
de números
reales con
exponentes
negativos con
la aplicación de
las reglas de
potenciación y
de radicación.
(P,A)
Prerrequisitos
-Organizar una lluvia de ideas sobre lo que
conocen del a potenciación y radicación.
Esquema conceptual de partida
-Presentar expresiones matemáticas de números
reales con exponentes positivos y negativos.
-Analizar la estructura de la expresión matemática.
-Identificar las expresiones con números negativos.
-Demostrar la procedencia de los exponentes
negativos
Construcción del conocimiento
-Elaborar tarjetas resumen con la información
obtenida.
-Ejemplificar el uso de los exponentes negativos.
-Realizar ejercicios de fijación.
-Contrastación de la información y procedimientos
aprendidos con la información del texto
Transferencia del conocimiento
-Resolver ejercicios asociados con la simplificación
de números reales con exponentes negativos.
Texto.
Tarjetas
memoria con las
leyes y
propiedades de
la potenciación
y multiplicación
Ejercicios
Indicador esencial de evaluación.
Aplica las reglas de la potenciación y
radicación en la simplificación de
expresiones numéricas con
exponentes negativos.
Indicadores de logro:
Elabora organizadores cognitivos.
Verbaliza y aplica propiedades.
Elabora ejemplos
Simplifica expresiones numéricas.
Técnica: Portafolio
Instrumento: Variados
EVALUACIÓN
1.- Completa los organizadores gráficos sobre las propiedades de los exponentes negativos.
2- Al frente de cada propiedad escribe un ejemplo de la misma.
3-Lee, analiza y resuelve expresiones con potenciación y radicación de números reales:
( 5. 2 ) -² =
( ¾ ) -³ =
{ -3 [ 5 -2]² : 4² + ( -3)³ (1/4)-³ =](https://image.slidesharecdn.com/plandeclasesmatematicas8-9-10-150318194308-conversion-gate01/85/Plan-de-clases-matematicas-8-9-10-47-320.jpg)
![EVALUACIÓN QUIMESTRAL
1.- D.C.D. Reconocer patrones de crecimiento lineal en tablas de valores y gráficos
Indica cuál es el patrón de crecimiento lineal considerando a siguientes tabla de valores
X Y
-1 +1
0 +2
1 +3
2 4
2.- D.C.D. Utilizar el teorema de Pitágoras en la resolución de triángulos rectángulos. (A)
Calcula cuánto mide la diagonal del siguiente cuadrilátero.
6m
8m
3.- D.C.D. Representar números racionales en notación decimal y fraccionaria
Completa el siguiente cuadro
4.- D.C.D. Simplificar expresiones de números racionales con la aplicación de las reglas de potenciación y de radicación (P,A)
(-3) (-3)² + [ ½ - 2 (- 2 + ¼)²] =
{ -4 : (5 – 3)³ - ( ¾ + ½ ): 2/3 )³ - 5}=
√ 125 : (3+2) - ( 2/3)³ + ( 5 -3 +10 – 7) =
DECIMAL FRACCIONARIO
12,5
3/ 4
1 ⅔
0,33
8,4](https://image.slidesharecdn.com/plandeclasesmatematicas8-9-10-150318194308-conversion-gate01/85/Plan-de-clases-matematicas-8-9-10-48-320.jpg)